基于服务商引导的综合能源系统源-荷协同优化方法

廖宗毅，万文略，陈曦，陈岚

(重庆理工大学电气与电子工程学院，重庆市 400054)

0 引 言

随着国家能源市场逐步开放，传统能源服务已难以适应新环境下用户的多元化需求，更多市场主体把注意力转移到更经济、高效的综合能源系统[1]。作为综合能源系统的终端应用形式，园区型综合能源系统(community integrated energy system，CIES)具有清洁高效、多负荷集中等特性，有利于可再生能源消纳，可通过优化调度策略发挥多能源互补优势与协同效益，具有很大的调度潜力，有关CIES优化运行的研究已成为热点[2-3]。

目前国内外关于CIES运行优化策略可概括为集中式与分布式两类。其中集中式优化策略大多基于综合需求响应(integrated demand response，IDR)机制引导需求侧调整用能、平缓负荷波动，实现多能协调互补。文献[4]考虑峰谷分时电价、天然气价格信号以及供热管网热惯性建立电气热IDR策略，提高了CIES的风、光消纳能力和能源利用率。文献[5]考虑CIES中多能流耦合特性和用户侧灵活负荷的响应潜力建立电气冷IDR策略，综合考虑供需两侧经济效益、负荷峰谷比以及碳排放等目标进行优化调度。文献[6]将分时热价、电价融入IDR策略中以提高CIES的清洁能源消纳能力与经济性。文献[7]引入电-气-热多能IDR策略，兼顾CIES经济成本、碳排放以及能效利用率建立多目标优化调度策略，提高了系统整体经济性。文献[8]以激励型IDR策略平衡多能流之间的需求并引入条件风险价值以兼顾CIES的经济性与安全性。以上研究通过IDR机制实现了系统经济运行、灵活调度，但仅将CIES作为价格接受者，未能充分挖掘其响应潜力，对上级能源网络与CIES的交互分析不足。

对于CIES的分布式优化，部分学者通过引入市场因素来实现。文献[9]提出了以综合能源销售商为领导者的主从博弈模型，对电、热价格进行联合优化从而引导各方能量交互，实现多主体分布式协同优化。文献[10]基于主从博弈方法构建区域综合能源系统服务商运行策略，以日前-日内两阶段价格信号激励，减小用户侧支出与负荷波动，提高服务商运行利润。文献[11]考虑能源供应商和用户的主动性，提出与供需双侧博弈互动下的园区运营商引导能源交互模型，在平衡三方主体需求与利益的基础上实现了CIES优化运行。文献[12]在工业用户、园区能量管理系统和上级电网之间构建集中-分布式IDR模型，在保护用户信息私密性的同时提高了系统整体经济性。在能源市场化背景下，上述研究对CIES源荷交互和多市场主体参与能源交易提供了重要的理论基础，但对价格机制的应用较少，且多数研究将负荷聚合商考虑为需求侧，尚未考虑用户主体的满意度与响应程度。

针对上述不足，本文提出基于综合能源服务商(integrated energy services provider,IESP)引导的CIES源-荷协同优化运行策略。在供给侧引入IESP以有机整合能源资源，协助上级能源网络引导多能协同灵活交易；综合考虑供能成本、CIES用能需求与需求响应程度等因素以确定电力、天然气价格范围，基于电网与CIES间联络线交互功率变化情况以及响应反馈信息优化电-气联合价格信号。在需求侧，对CIES的可转移电、气负荷以及建筑物虚拟储热特性建立电气热联合的IDR策略；在兼顾CIES用能经济性、满意度以及响应合理性的同时，将响应信息反馈给上层IESP。将上述源荷交互过程划分为“优化定价”与“经济调度”2个层级，引入粒子群-混合整数线性规划的双层优化算法进行分层式优化与迭代，从而实现求解。最后，由算例仿真验证所提策略对挖掘CIES调度潜力、提升系统整体经济性等方面的有效性。

1 用户侧园区综合能源系统模型

1.1 CIES建模

以冷热电联产机组、光伏、风机、电制冷及电制热机等设备为基础构建CIES，采用“并网不上网”运行方式，具体架构如图1所示。

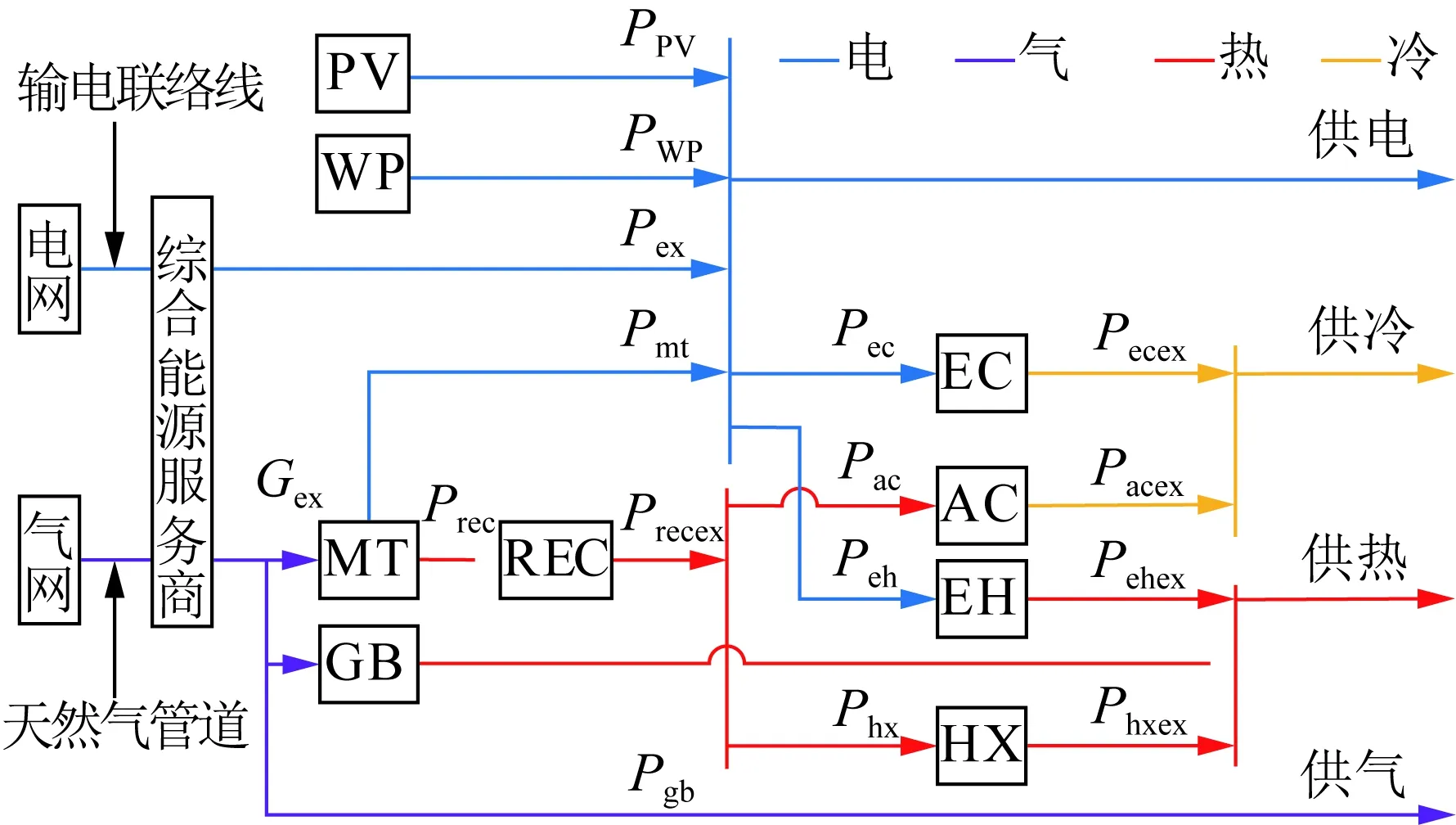
图1 CIES架构Fig.1 Architecture of CIES

1.1.1 冷热电联产

冷热电联产系统由微型燃气轮机、余热锅炉和吸收式制冷机等设备组成，其数学模型为：

(1)

(2)

(3)

(4)

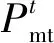
1.1.2 电制冷与电制热机

(5)

(6)

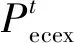
1.1.3 光伏与风机

(7)

(8)

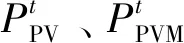
本文对风机和光伏出力暂不考虑预测误差及突发气象状况等影响。

1.1.4 燃气锅炉

燃气锅炉消耗天然气以满足用户热能需求，其模型表示为：

(9)

1.2 IDR模型

需求响应机制可引导需求侧改进固有调度计划、实现多能协调、优化负荷曲线。CIES的能源消耗主要为天然气与电力，二者均为现代能源系统的重要资源，具有相似的商品属性，可基于需求弹性策略建立电、气负荷的需求响应模型[13]。此外，为进一步挖掘用户调度潜力，考虑建筑维护结构的虚拟储热特性，对用户热负荷构建热能需求响应模型。

1.2.1 电、气需求响应

以目前应用较广泛的需求价格弹性法描述负荷的需求量与价格之间的关系。以电能为例，其需求响应模型可表示为：

Pload,dr=Pload,o+ΔPload

(10)

式中：Pload,o、Pload,dr分别为原始条件下以及响应后的用户侧电力负荷需求；ΔPload为电负荷变化量，其与电价的变化量之间存在以下关系。

ΔPload,N=MPΔJPN

(11)

(12)

(13)

(14)

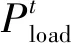
考虑需求响应的合理性，对用户参与互动时每时段电、气负荷可响应范围做以下约束：

(15)

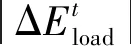
1.2.2 热能需求响应

不同于电能、天然气，热能的消耗在时间尺度上具有一定惯性，其本质是建筑物维护结构对热能的储存性。根据文献[15]可得室内环境热平衡方程为：

(16)

式中：ΔQ为室内热量的变化量；k=cλ，其中c为空气比热容，λ为空气密度；V为室内空气体积；Tin为室内温度；τ表示热能平衡方程的时间步长，为便于热能供需平衡的计算，本文取为1 h。

忽略太阳辐射热功率的影响，影响建筑内部热量的主要因素为室内外温差与制热设备的输出热功率。考虑系统制热的情况下，式(16)可写为：

(17)

式中：kwl为建筑墙体维护结构的传热系数；fwl为建筑的外墙面积；kwn、fwn分别为建筑外窗的传热系数与面积；Tout为室外温度；QH为系统中供暖设备的制热功率。热能需求响应模型具体内容参考文献[16-17]。

2 IESP引导源-荷协同优化模型

目前有关CIES运行优化研究多以电网为核心，用户的设备、用能需求与满意度等私密信息均由电网掌握，降低了用户的参与意愿，亦无法充分调用响应资源。为此本文引入IESP，使其担任系统源-荷交互的桥梁；考虑由IESP获取用户侧需求与响应满意度等信息，将电力、天然气交易有机结合以充分调动用户响应积极性，通过优化能源价格信号引导能源交互，实现合理、高效的源-荷协同优化，具体框架如图2所示。

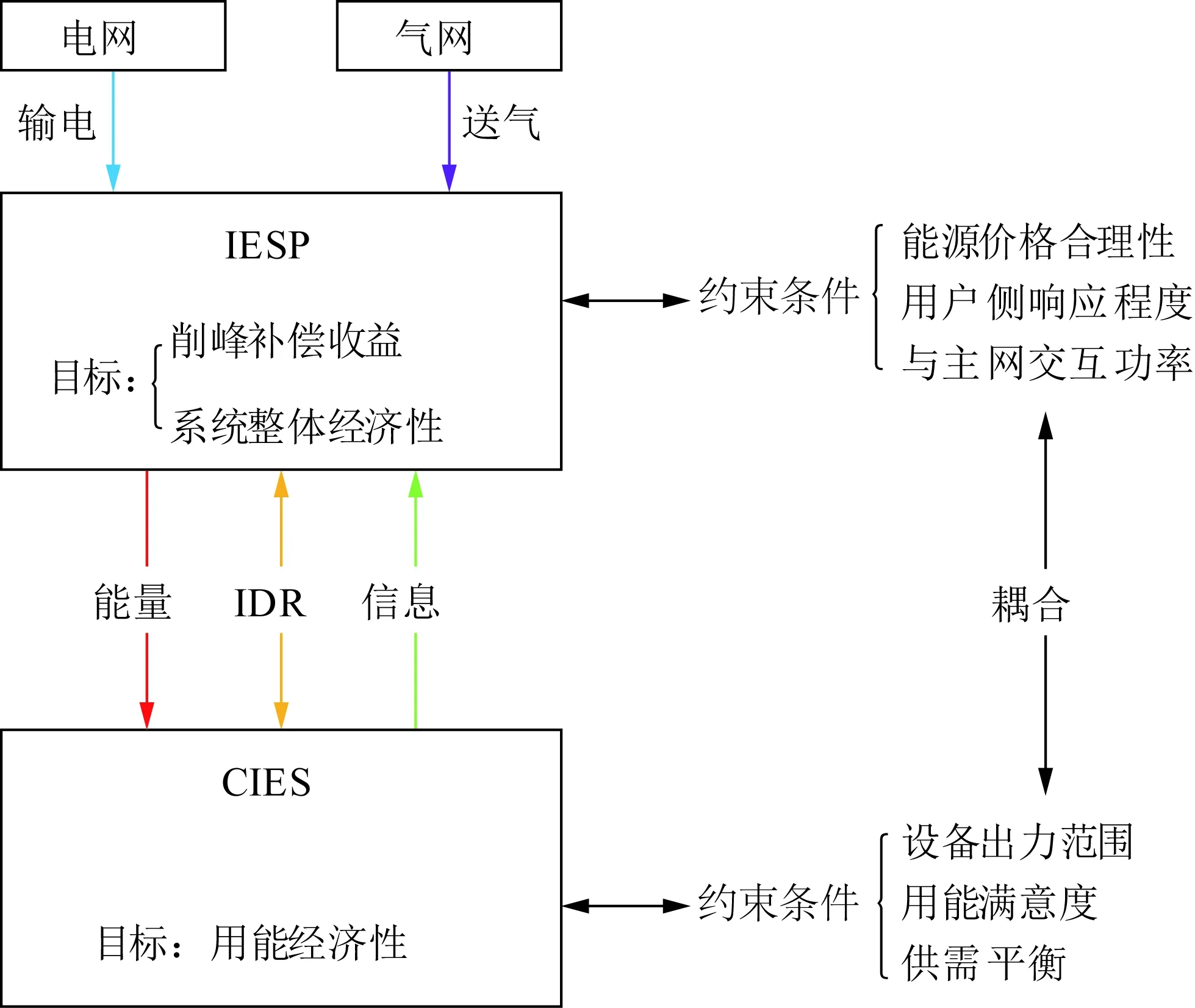
图2 IESP引导源-荷交互Fig.2 IESP guidance of source-load interaction

整个系统的源荷交互包括“优化定价”与“经济调度”2个层级，二者之间互相影响，通过循环迭代求解。首先，上层的IESP作为源荷交互的载体，为充分调动CIES响应积极性，将电力、天然气交易有机结合；综合考虑供能成本、用户需求信息等因素以确定电力、天然气价格上下限；综合考虑联络线输电功率变化情况与用户响应信息反馈以优化电-气联合价格信号。而下层的CIES将根据价格信号自发转移用能需求，在满足设备出力范围、供需平衡等约束的基础上进行经济调度，并向IESP进行信息反馈。

2.1 决策变量

该源-荷协同优化模型本质上是一个非线性优化问题，问题的决策变量为IESP给定的电力、天然气价格信号以及CIES用能需求。

2.2 约束条件

由于综合能源系统中电-气能源耦合特性，二者负荷需求与价格信号的交互作用较为复杂，为保证源荷交互的合理性，给出相关约束。

2.2.1 源-荷互动约束

1)价格范围约束：IESP优化电力、天然气价格信号时，为保障供能网络的利益以及CIES需求响应合理性，须综合考虑CIES参与互动时负荷的最大可移动程度，以及电力、天然气的成本。

以电价为例，价格上限可由用电峰时段的负荷及其对应的最大可移出水平结合上文需求响应模型得出。考虑定价合理性，任何时刻能源价格都应该大于其供应成本；确定价格下限时须在考虑谷时段最大移入负荷的基础上兼顾售电利益，取理论下限值与电价成本之间的最大值。

(18)

(19)

(20)

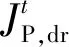
2)峰谷价格比约束：为防止用户侧参与需求响应程度不足或响应过度以致峰谷倒置，须对天然气的峰谷价格做出约束。

K1≤JGp/JGv≤K2

(21)

式中：JGp、JGv分别表示天然气峰时、谷时价格；K2、K1分别为最大、最小峰谷价格比值。

2.2.2 用户侧约束

1)设备出力与供需平衡约束。CIES设备须在合理的出力范围内运行。

(22)

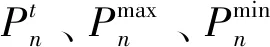
除设备出力约束之外，须满足用户侧的电、气、冷、热、烟气等能量母线的供需平衡约束。

(23)

(24)

(25)

(26)

(27)

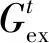
2)日负荷总量约束。为保证用户侧用能需求，对参与响应前后负荷总量的变化做以下约束：

(28)

3)用能满意度约束。为保证用户的用能满意度，对电力、天然气用能添加满意度约束[14]：

(29)

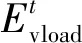
4)用能成本约束。用户侧须支出的总费用包括满足用能需求所必要的购能成本以及园区内设备的运维成本。

CUP=CUB+CUM

(30)

(31)

(32)

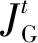
用户希望参与IESP价格引导时，其总经济支出是低于原始情景下的，所以用户侧经济成本约束为：

(33)

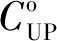
2.3 供能端需求约束

1)削峰填谷约束。IESP引导源-荷协同优化的目的是削减联络线输电功率峰谷差、优化配置系统资源，要求IESP引导互动后，电网与用户间的联络线输电功率峰谷差减小，日负荷率提高。

(34)

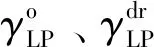
2)售能满意度约束。考虑到供能网络的利益诉求，须对IESP进行价格优化后电网、气网的售能收益变化进行约束。

(35)

(36)

SPCmin≤SPC

(37)

SGCmin≤SGC

(38)

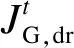
2.4 目标函数

IESP引导源荷互动，对电网与CIES间联络线输电功率进行“削峰填谷”，其收益来源为电网削峰补偿激励，即目标函数为：

(39)

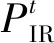
3 求解方法

不同于传统经济调度问题，基于IESP引导的源-荷协同优化模型中的优化定价、需求响应、经济调度等问题相互耦合，存在较多双线性项，难以通过常规优化方法解决。为此本文提出一种粒子群算法结合混合整数线性规划(particle swarm optimization and mixed integer linear programming,PSO-MILP)的双层优化求解方法，具体的求解流程如图3所示。

IESP的价格信号优化与CIES响应行为组成了一个大规模非线性优化问题，采用粒子群算法可以提高可行解搜索能力，降低问题复杂度。内层是以园区的设备出力范围与能源网络供需平衡为约束的，基于经济成本最小化考虑的线性规划问题；将内层CIES经济调度的结果放入外层进行检验计算，以简化内层的MILP问题复杂程度。在此基础上，将CIES用能成本、用能满意度以及供能端“削峰填谷”等约束以罚函数的形式嵌入粒子的适应度中进行计算，可一定程度上改进算法的求解性能。粒子群算法中种群数设为100，最大迭代次数为100次，采用文献[18]的惯性权重指数递减策略，权重初值与终值分别设为1.0与0.5，粒子自学习率与种群学习率均为2。在场景A、B中，能源价格粒子的维度为27维，一天24个时段分时电价信号占24维，峰谷平天然气价格信号占3维，天然气价的峰谷时段划分参考文献[7]。场景C、D中，价格粒子为48维变量，即24时段的分时电价信号、分时气价信号。考虑到48维价格粒子产生的可行解范围较大，为提高算法的可行解搜索能力，对每个种群中的最优个体粒子引入反向学习策略[19]，生成精英个体反向解以增加粒子种群多样性。此外，为提高用户满意度，每次迭代过程中将式(28)、(29)及式(34)—(38)等约束条件以罚函数因子写入粒子适应值中。

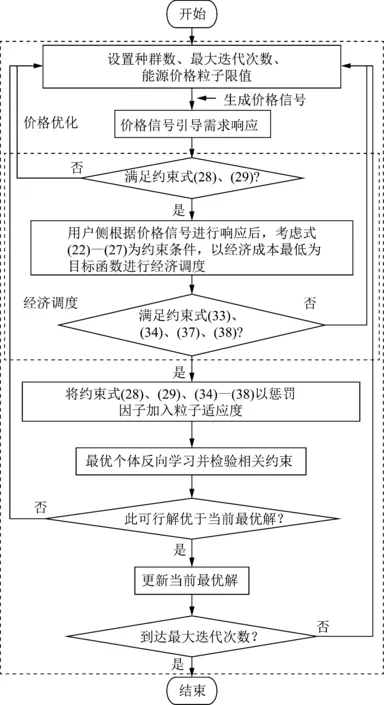
图3 PSO-MILP双层优化求解流程Fig.3 Solution flow of PSO-MILP bi-level optimization

4 算例分析

本文CIES架构模型及负荷等数据参考了文献[4,7,20]，设备具体参数见表1、表2。内层MILP的Gap设为1×10-5，迭代计算所得结果中未出现违反模型以及表1中所提等式/不等式约束的情况。电价弹性矩阵的自弹性系数为-0.10，交叉弹性系数为0.01，天然气价弹性矩阵自弹性系数取-0.20，交叉弹性系数取0.01[11,21]。热能需求响应模型中建筑维护结构参数如表3所示，空气比热容c与空气密度λ分别为1 000 J/(kg·℃)和1.2 kg/m3，室内空气体积V为25 600 m3。CIES负荷的最大可移动水平fmove取10%[14]。设供能端售电单位成本为0.4元/(kW·h)，天然气单位成本为1.3元/m3。设IESP削峰补偿单价为6元/(kW·h)，日负荷率每提升1%补偿60元。天然气峰谷分时价格约束中K1取1，K2取3。日负荷总量约束中的松弛系数φ取0.01[22]。用户侧满意度约束中[14]，用电最低满意度SUPmin与用气最低满意度SUGmin均设为0.95。电网售能收益最低满意度SPCmin与天然气网收益最低满意度SGCmin均设为0.90。为验证所提模型的有效性，给出5个场景以分析源荷交互行为；其中场景O即为原始场景，场景A—D对应于IESP采用4种不同的价格信号与IDR策略，场景具体条件设置见表4。

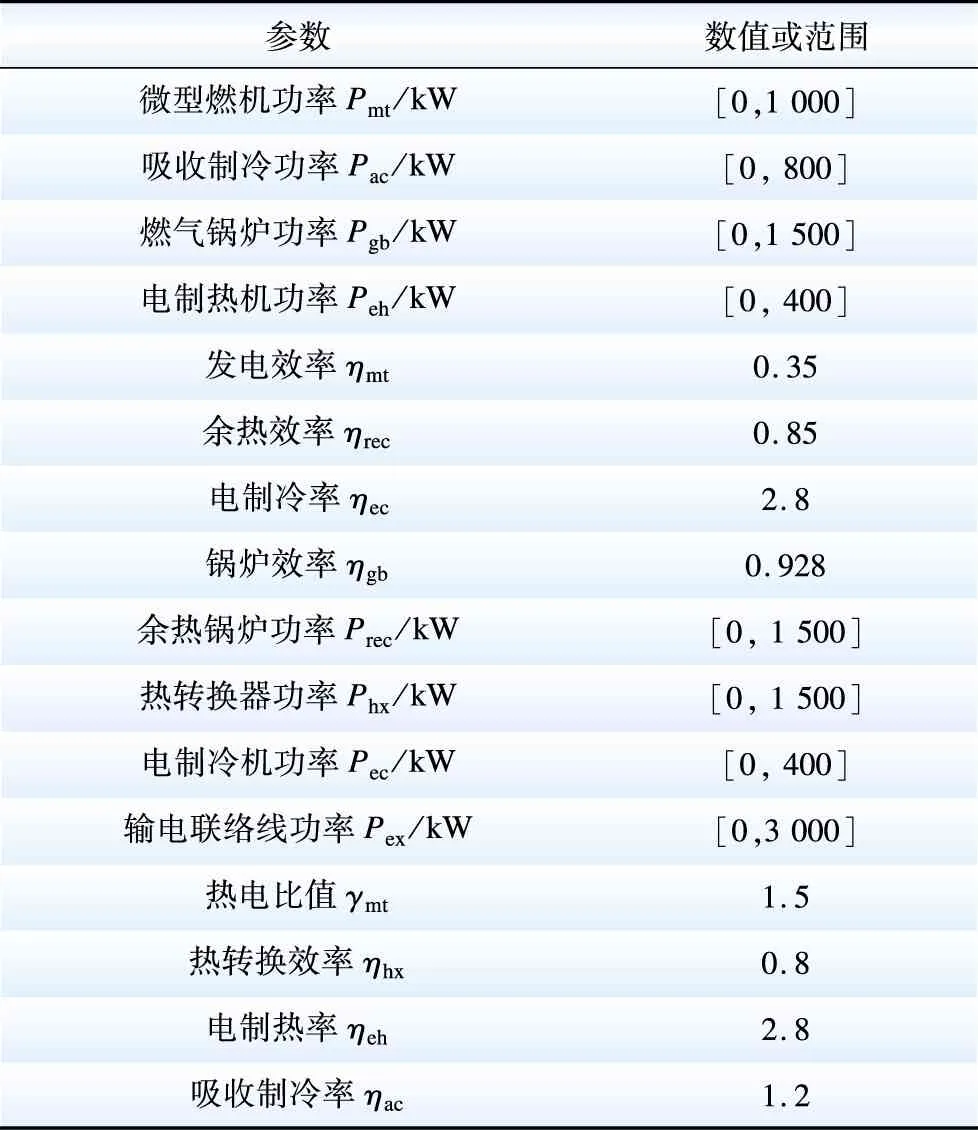
表1 设备出力范围与运行参数Table 1 Equipment output and operation parameters

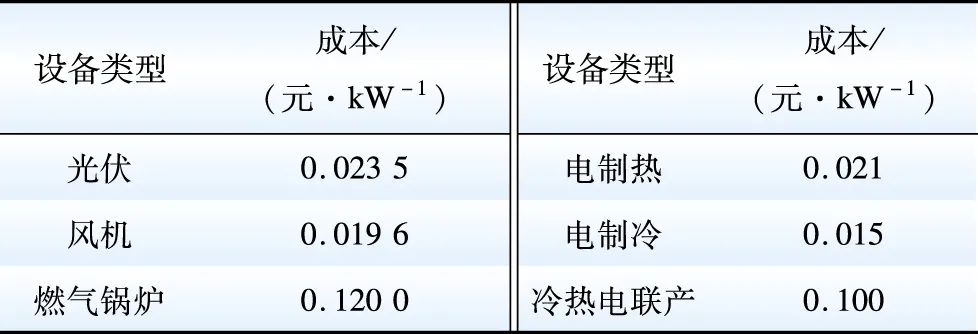
表2 设备单位出力运维成本Table 2 Operation and maintenance cost per unit output of equipment

表3 建筑维护结构参数Table 3 Structural parameters of building maintenance

表4 场景信息Table 4 Scene information

4.1 源-荷交互分析

图4为PSO-MILP双层优化在求解该问题时的粒子收敛情况。算法经过约50次迭代后几乎实现收敛，而实际上在第45次迭代时，电网与天然气公司的收益已逼近最后的收敛结果，但后续迭代过程中收益曲线又有轻微波动。这是由于源-荷协同优化模型中IESP致力于系统整体经济性的优化，即使某些迭代过程中电网与天然气公司收益相同，但价格信号、输电联络线的日负荷率和削峰容量等也可能不同。此外，需要注意的是，粒子的适应度是在IESP削峰补偿收益值的基础上加入了用户侧经济性、供能端收益以及“削峰填谷”等各方经济诉求所构成的惩罚因子值，所以适应度本身并不等于IESP的收益，电网与天然气公司两大能源供应商的收益曲线也并非完全对应于粒子的收敛趋势。

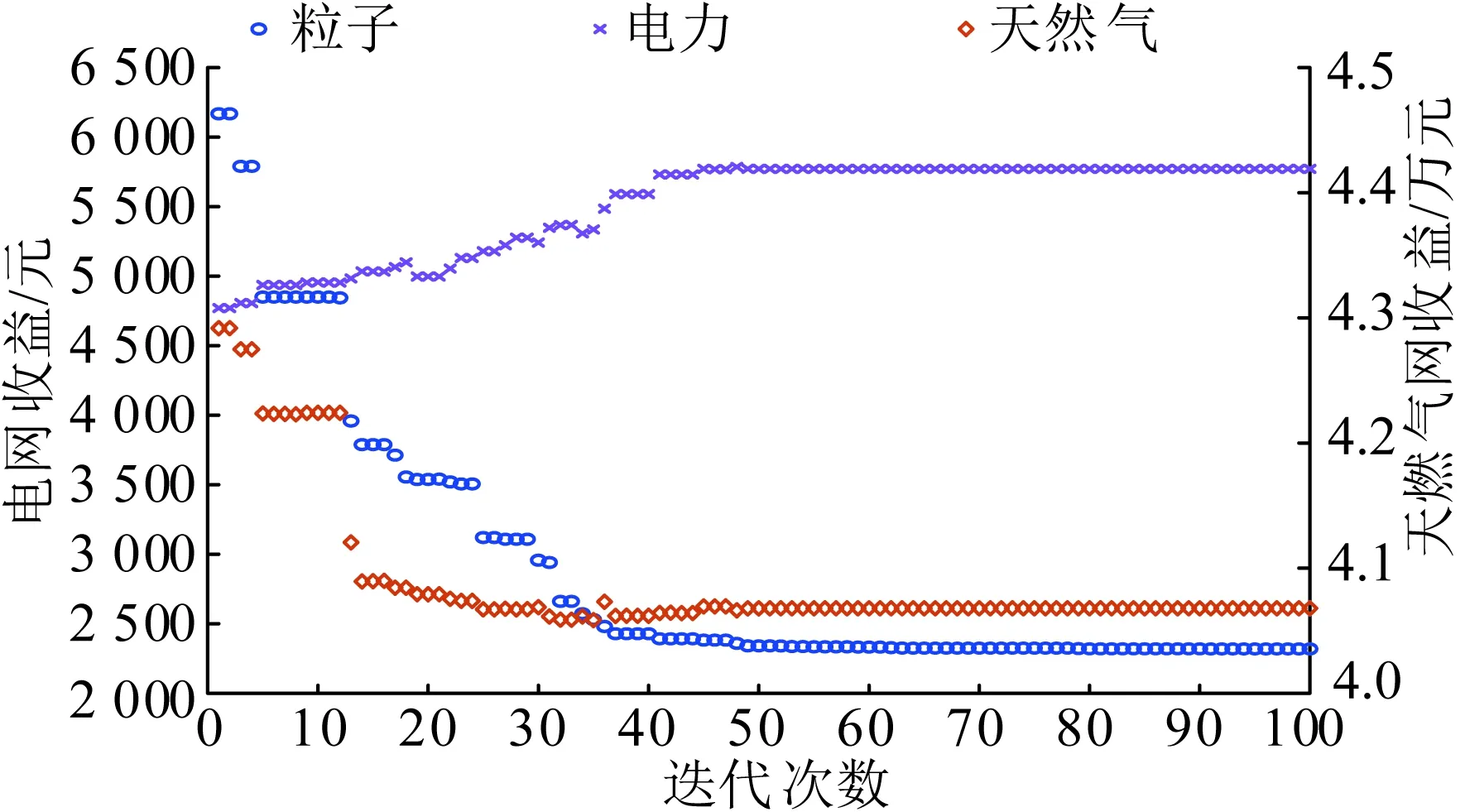
图4 PSO-MILP可行解收敛情况Fig.4 Convergence of PSO-MILP feasible solution

IESP同时对电价、气价进行优化，在满足CIES用能经济性、满意度、响应程度、设备出力情况、供需平衡等条件的基础上，对园区调度计划与用能方式进行了调整，使联络线电交互功率峰谷差减小，功率曲线更平缓。不同场景下的结果对比如表5所示。

由表5知，在不考虑IESP参与的原始场景O中，CIES与电网联络线的电交互功率峰负荷与峰谷差均为1 448.32 kW，而经IESP引导后峰负荷均有所下降。其中，场景C下的峰负荷降低较明显，为1 367.23 kW；场景D下峰谷差削减程度最大，由1 448.32 kW削减至1 239.15 kW；场景B下负荷率最高，由原始的32.51%提升至39.78%。任意情景下的CIES用电满意度SUP与用气满意度SUG、电网收益满意度SPC以及天然气网收益满意度SPC均满足模型所提相关约束。但场景C下CIES的用能满意度最高，分别为0.988和0.978；电网的售能满意度为对照组中最低值，仅0.900；而天然气网售能收益满意度较高，达0.975。实际上，由于解空间搜索范围以及DR灵活性的不同，在有限次迭代中求解出的各场景下能量交互策略与调度结果呈现一定差异。但结合表4、5进行分析不难发现，场景D中的48维价格信号与3种DR策略所对应的粒子群搜索空间最广，届时IESP在同样量级的迭代计算中找到的可行解获利1 487.05元，高于其余所有场景，实现了其自身利益的最大化；而相较于场景D，采用与之相同DR策略、不同价格信号维度的场景B中，IESP的收益则略有下滑，电网、天然气公司的满意度也降低；这是由于可行解的搜索空间缩小，有限次迭代得出的交互结果在整体上变差；此外，纵观场景B、D下CIES的支出也能发现，由于场景D的可行解搜索范围更大，IESP在兼顾自身以及供能网络利益的基础上压缩CIES的经济支出；即使该模型中的式(33)已向CIES保证其参与互动后的经济性，但IESP仍在约束范围内企图让CIES支出更多以追求自身以及供能网络等上层主体的利益。

此外，若考虑不同DR策略的灵活性，可见场景A、C下均未考虑热能DR，可知场景A的价格信号空间搜索范围以及DR策略都是最差、最有限的，届时在同样规模的迭代计算中，IESP找到的解所对应的收益也更低。而相比于场景D，场景C虽然价格信号同型但未计及热能DR，在同样的价格信号搜索空间内取得了较高的收益，甚至通过价格激励使其削峰容量达到最高，但其对输电联络线负载功率的平缓效果并不如场景D，究其根本是DR灵活性的不足使其解空间“隐性”的缩小了。

由于篇幅限制，下文仅对场景D下的IESP引导互动效果以及CIES调度计划做具体说明，其余场景的价格信号优化与引导互动见附图A1—A4。场景D下的优化结果如图5、6所示。结合图6与表5可知，原始情景下01：00—04：00时段的联络线电交互功率为0，经IESP引导后略有提高。设19：00—21：00时段为用电高峰期，考虑由IESP对此时段内电交互功率进行削减，3个时段总削峰容量为189.1 kW·h，日负荷率提高了6.77%。届时，用户侧CIES总经济成本降低，电网与气网收益均有所下降，IESP从电网侧获取了1 487.05元削峰补偿。

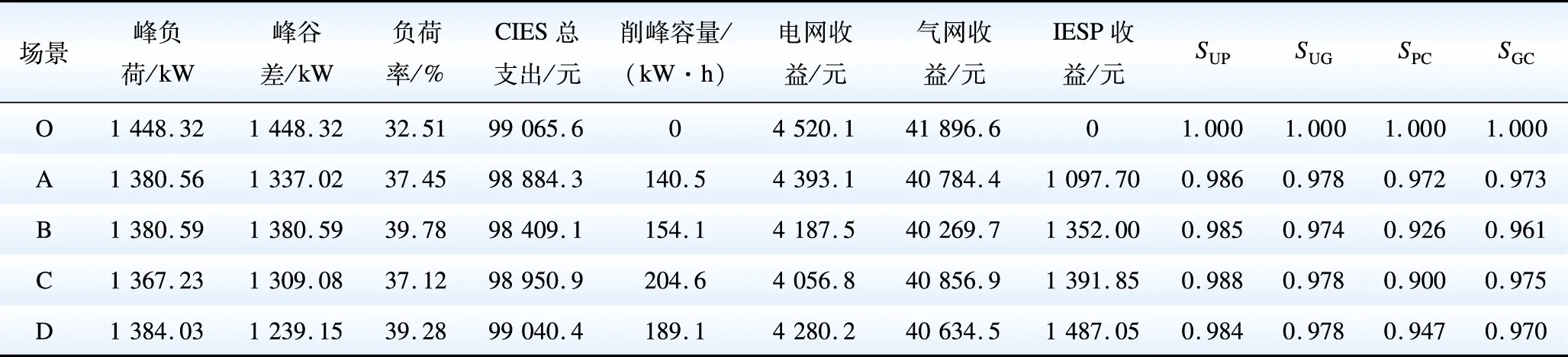
表5 不同引导方式结果对比Table 5 Comparison of the results of different guidance modes

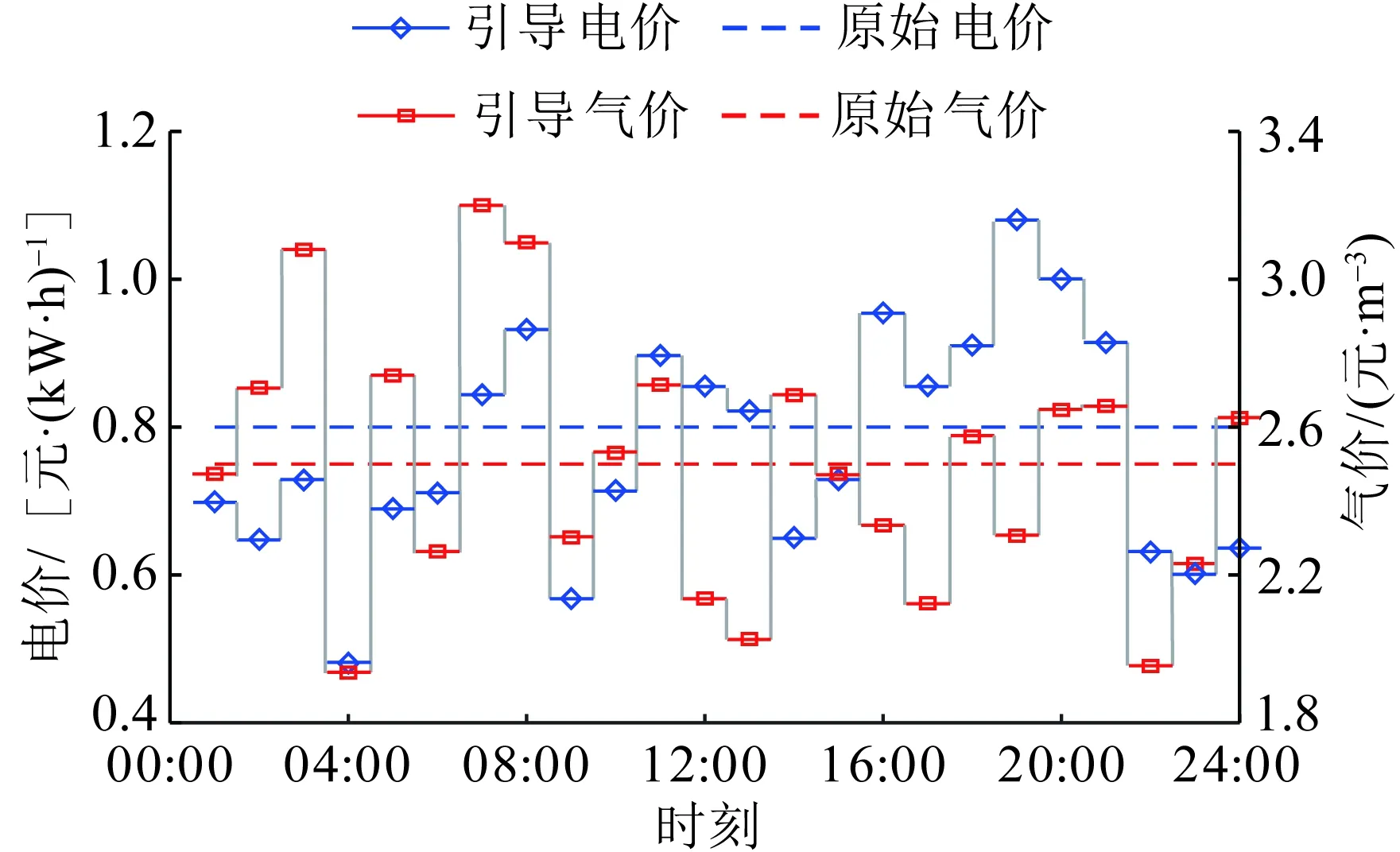
图5 场景D下IESP价格信号Fig.5 IESP price signal in scenario D

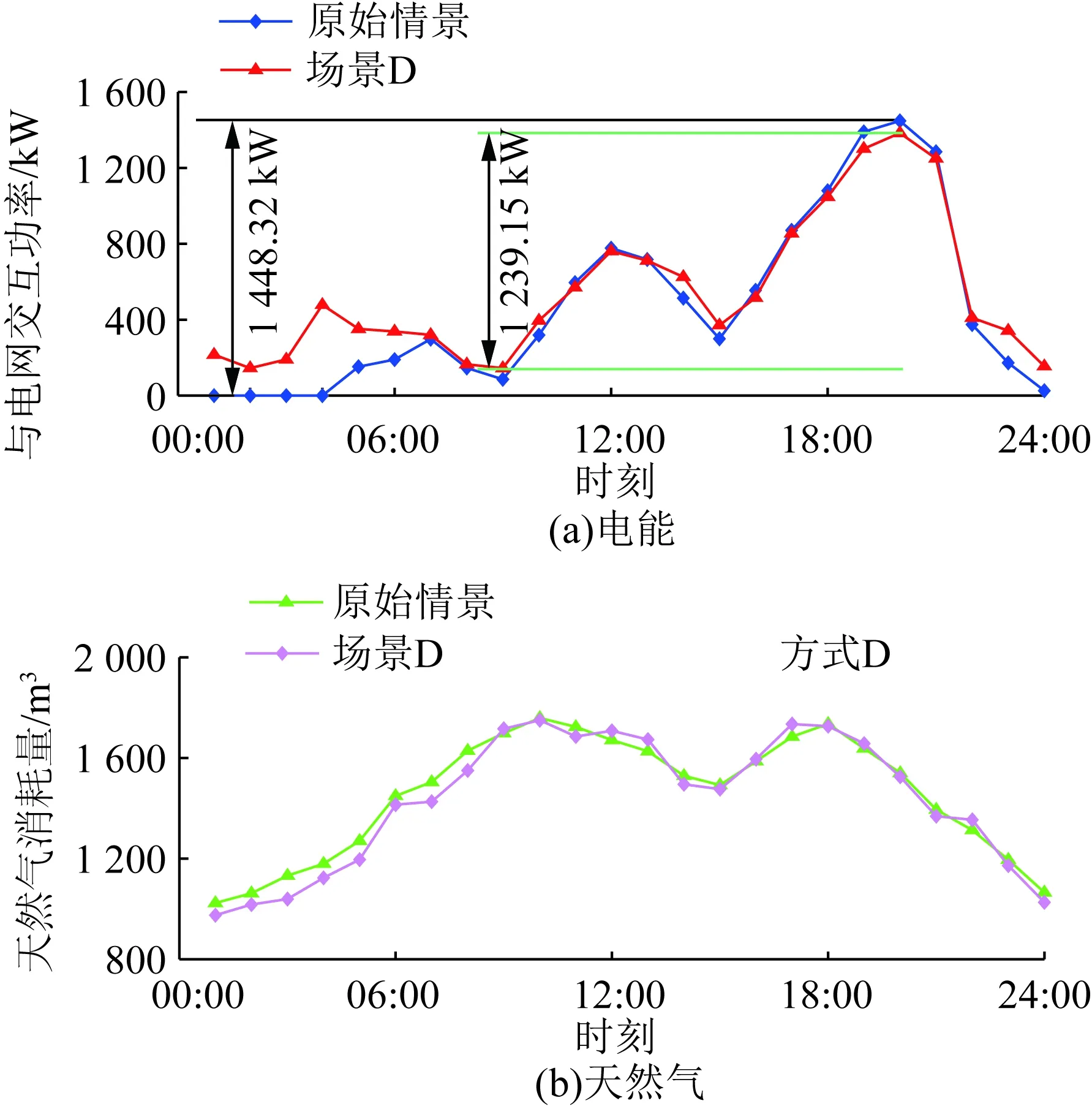
图6 场景D下IESP引导效果Fig.6 IESP guidance effect in scenario D

总的来说，5种情景下各方收益均有不同，相比于原始情景，考虑IESP参与交易时电网、气网收益均受了一定影响。但是对系统整体而言，经IESP引导后电网与CIES联络线电交互功率曲线更加平缓，实现了“削峰填谷”，IESP以灵活的价格机制深度挖掘了CIES调度潜力，使源荷交互更灵活高效，提高了系统整体经济性。

4.2 CIES经济调度分析

图7—10为考虑IESP引导时系统的能源母线供需情况。园区供能网络中存在能源转化装置，在满足自身用能需求的前提下将以经济成本最低为目标进行调度，合理调整各个设备的启停与出力。结合图5可知，CIES对IESP的价格信号的响应情况，CIES满足自身用能需求的基础上为追求经济性自发转移了部分用能需求。由图7结合图5可见，19：00—20：00时段电力价格略高于原始情景时，用户削减了部分电负荷，而22:00时段的电价有明显降低，该时段用电需求得以提升。01：00—06：00时段电价较低，用户提高了电负荷并开启电制热装置。

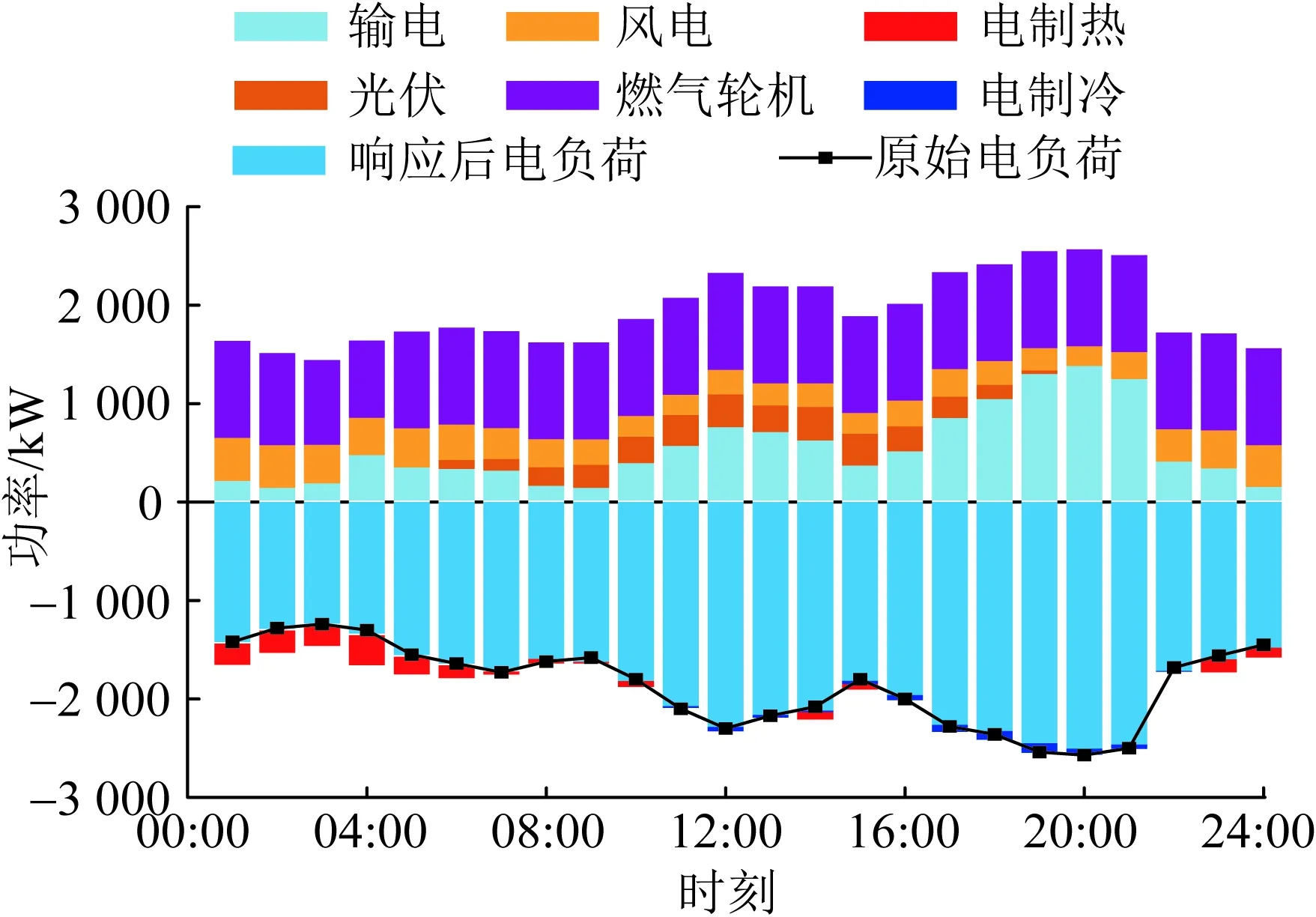
图7 电能供需平衡Fig.7 Balance of power supply and demand

由图8，结合图5可见，相比于原始情景，12：00—13：00时段天然气价格降低，用户将一定量天然气需求转移到该时段上并开启燃气锅炉以补充热能。

图9为系统热能供需情况，考虑建筑虚拟储能特性，部分时段热能需求有一定转移。图10为系统冷能供需情况，CIES以吸收式制冷与电制冷设备共同供给用冷需求。整个系统供能网络全部满足出力范围与供需平衡约束，CIES通过合理安排设备调度计划实现了经济调度。

图11为CIES的建筑内外环境温度。室外环境温度已知，室内由系统制热设备供给热能，综合考虑建筑维护结构面积与传热系数等因素，可知CIES室内温度为15～17 ℃。

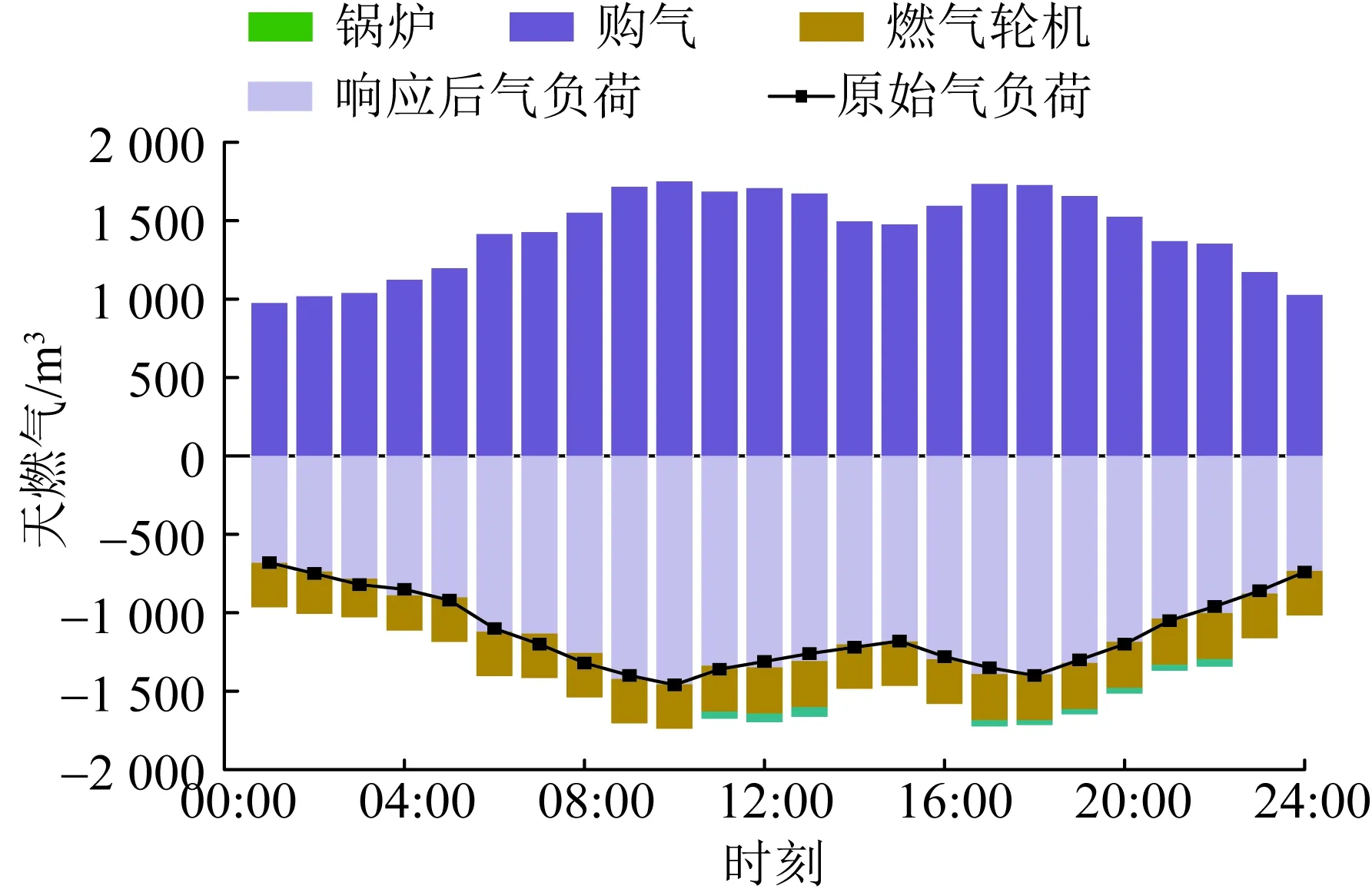
图8 天然气供需平衡Fig.8 Balance of natural gas supply and demand

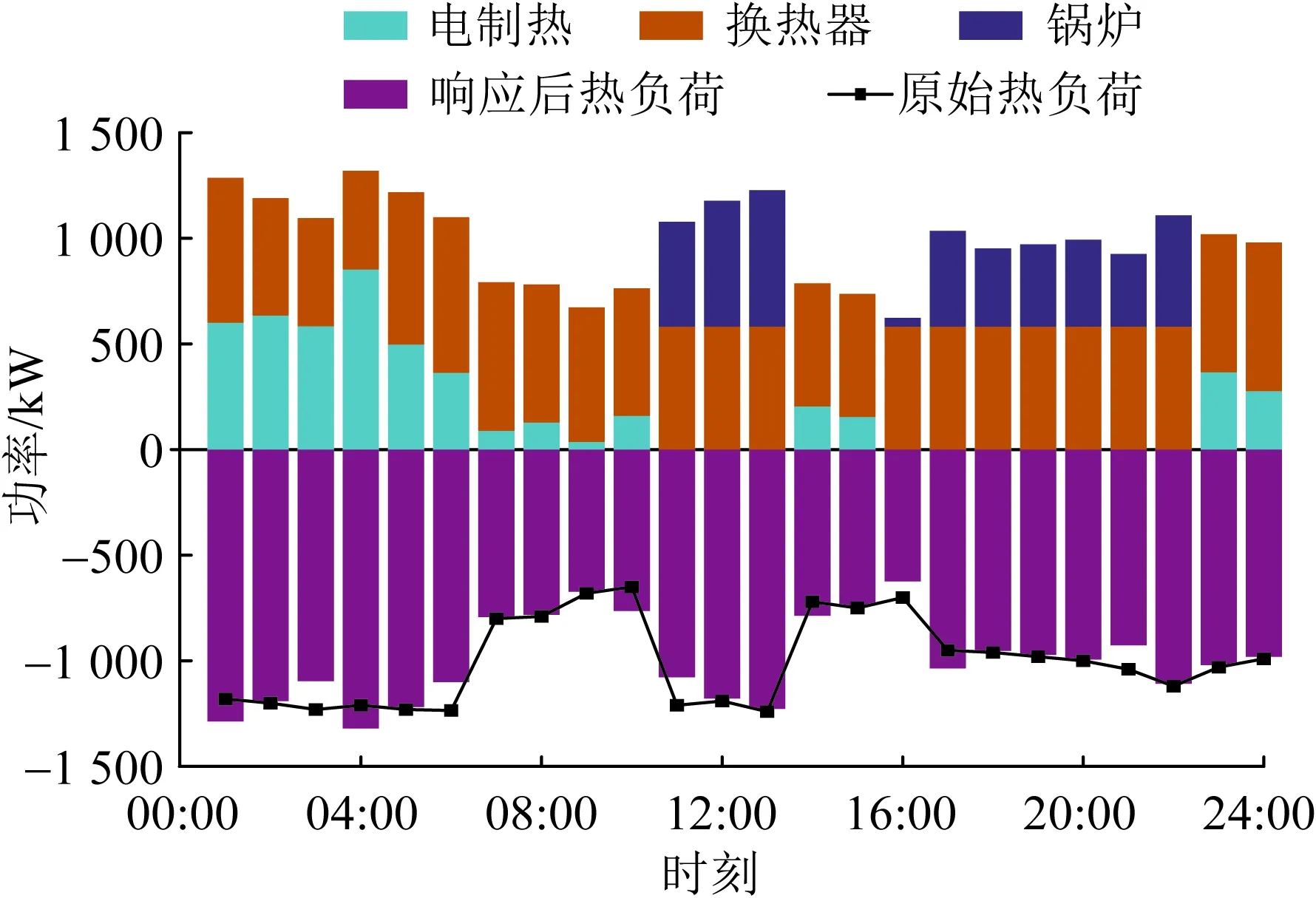
图9 热能供需平衡Fig.9 Heat energy supply and demand balance

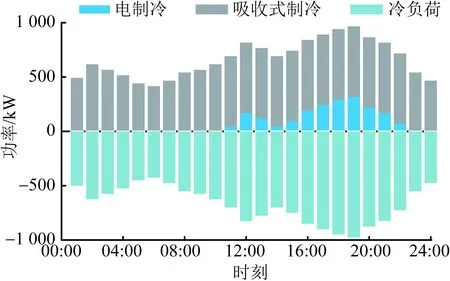
图10 冷能供需平衡 Fig.10 Cooling energy supply and demand balance

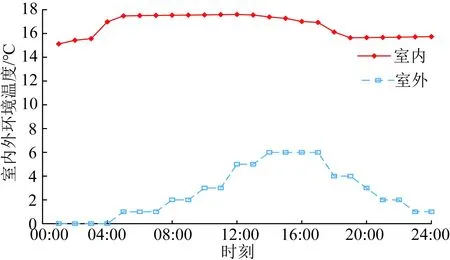
图11 CIES室内外温度Fig.11 Indoor and outdoor temperature in CIES

5 结 论

本文提出基于IESP引导的CIES源-荷协同优化模型。在需求侧，基于可转移电、气负荷以及建筑虚拟储热特性建立电气热IDR策略以挖掘CIES调度潜力；在供给侧引入IESP以引导多能协同灵活交易，综合CIES与电网间联络线交互功率变化情况、CIES用能需求以及响应反馈信息以优化电-气联合价格。通过PSO-MILP双层优化算法对模型进行分层优化、循环迭代求解。最后以算例仿真验证了所提模型与方法的有效性，得到以下结论：

1)以IESP作为源荷交互载体并引入电-气联合价格引导机制，可深度激发CIES响应积极性以实现源荷协调交互；在保障CIES参与满意度、用能经济性的基础上充分挖掘其调度潜力，对CIES与主网联络线电交互功率进行“削峰填谷”，提高系统整体经济性。

2)PSO-MILP双层优化算法可对所提模型中的源荷交互行为进行分层优化，循环迭代求解。PSO的自趋优性与群体性可协助IESP进行价格信号可行解的搜索；经济调度层采用MILP可保证CIES满足供需平衡与设备出力等约束；“优化定价”与“经济调度”两阶段的循环迭代可保证源荷交互合理性，与此同时解决了IESP价格、CIES的需求及IDR等行为中存在的双线性项问题。

本文所提模型基于CIES多能源IDR策略及IESP价格机制对源荷交互行为进行刻画，对园区调度潜力进行了挖掘，改善了系统整体经济性。但所用求解算法中粒子的适应度包含着用户、供能端的各种满意度约束的惩罚因子，此为智能优化算法的固有问题，即解的随机性与弱可解释性；智能优化算法虽然在实际工程与各类文献中广泛应用，为大量高维度的非凸、非多项式问题提供了解决办法，但其对罚函数的处理以及固有的随机搜索特性使求解的稳定性与可解释性有限。此外，所提模型对CIES的储能以及向上层电网售电等情况考虑不足，下一阶段将围绕以上问题进行改进。