碳中和愿景下考虑电氢耦合的风光场站氢储能优化配置

许传博，赵云灏，王晓晨，柯毅明

(1.华北电力大学经济与管理学院，北京市 102206；2.新能源电力与低碳发展研究北京市重点实验室(华北电力大学)，北京市 102206；3.华北电力大学国家能源发展战略研究院，北京市 102206；4.国网能源研究院有限公司，北京市 102209；5.暨南大学国际能源学院，广东省珠海市 519070)

0 引 言

构建清洁低碳、安全高效的能源体系是实现我国碳中和目标的关键举措。储能是推动主体能源由化石能源向新能源更替的关键技术，也是提升传统电力系统安全性、灵活性和经济性的重要手段[1]。2021年4月，国家发改委、国家能源局发布了《关于加快推动新型储能发展的指导意见(征求意见稿)》，为推动新型储能的发展指明了方向。近年来，为进一步促进新能源消纳，发电侧“新能源场站+大规模储能”这种典型应用场景受到众多关注[2]。但电能作为能源载体具有明显的储存局限性，即无法大规模、长周期地储存，而氢能则可以有效弥补电能储存的缺陷[3]。因此，面对新能源出力的随机性和间歇性特征，氢能与电能的耦合可支撑更高渗透率的新能源发展。

储能容量的合理配置是发电侧风光场站规划设计阶段的重要内容，对改善新能源发电质量和减少弃风、弃光等方面具有重要的指导意义[4]。当前，发电侧储能优化配置的研究成果十分丰硕。文献[5]针对风光发电系统建立了储能容量配置的双层决策模型，外层规划模型目标为储能的初始投资与联络线波动惩罚最低，内层规划模型目标为系统联络线功率波动最低；文献[6]基于鲁棒优化理论刻画了发电侧可再生能源出力的不确定性，并计及分时电价以储能侧全生命周期成本、系统内总发电成本、联络线功率波动最小为目标配置储能容量；文献[7]以弃风率为约束，以储能投资成本最小为目标，基于分布鲁棒优化求解了考虑风电不确定性的风电场储能容量配置问题；文献[8]基于精细化时序运行模拟分析流程，以系统总成本最低为优化目标，考虑投资决策约束和运行约束，对不同成本情景下电源和储能的最优容量进行了配置优化。

除此之外，还有学者考虑发电侧的混合储能优化配置，如文献[9]以储能系统全生命周期净收益最大为目标，构建了风光电站内容量型和功率型储能系统混合配置优化模型，随后采用遗传进行求解；文献[10]以平滑效果最优与投资成本最低为目标函数，构建了蓄电池和超级电容器混合储能的容量优化配置模型，同样采用遗传算法求解最优容量配置方案；文献[11]提出由压缩空气储能、锂电池和超级电容器组成的混合储能系统，建立了3种储能的数学模型，并针对其不同的特性，提出了基于连续性运行的容量优化配置方法；文献[12]针对蓄电池和超级电容器的混合储能系统，提出了非并网风电/储能/本地用户系统的混合储能系统配置的多目标优化模型；文献[13]以售电收益最高为优化目标，采用蚁狮算法对风电集群联合储能系统的最优容量配置进行求解；文献[14]以光伏电站、小水电站和抽水蓄能电站为主体的混合能源系统为研究对象，提出以系统投资成本最小为上层目标函数和以系统获得售电收益最大为下层目标函数的双层规划模型。然而，上述研究配置的储能种类主要是电化学储能、超级电容器储能、抽水蓄能、压缩空气储能等，尚未涉及到氢储能。当前，氢储能应用研究主要集中在电网侧[15-16]和用户侧[17-19]，且多忽略了碳减排效益。相对而言，考虑碳减排的发电侧氢储能配置优化研究十分匮乏。

综上，在发电侧储能优化配置的相关研究中，其优化目标主要有售电收益、储能投资成本或出力波动性，约束主要考虑了弃电率指标。但尚未有研究同时考虑氢储能投资成本最小、系统累计跟踪计划误差最小和二氧化碳减排量增量最大等目标。与此同时，优化模型中还需要考虑有限的场地面积等实际约束条件。此外，关于发电侧的氢储能配置优化还需要进一步研究。因此，本文研究电氢耦合下的风光场站氢储能优化配置问题。首先，以氢储能投资成本最小、系统累计跟踪计划误差最小和二氧化碳减排量增量最大为目标函数，以弃电率和场地面积为约束条件，构建带约束的多目标整数规划模型；其次，收集甘肃省嘉峪关市某区域的风光资源、温度等数据；随后，采用带精英策略的非支配排序的遗传算法(non-dominated sorting genetic algorithm-II,NSGA-II)对规划模型进行求解；最后，采用熵权法和加权平均法对帕累托解进行排序。

1 模型构建

1.1 风光场站及氢储能功率模型构建

1.1.1 光伏功率模型

光伏面板的实际发电功率主要受到太阳辐射强度和环境温度的影响。具体计算模型如式(1)所示：

(1)

式中：PPV(t)是光伏面板的实际发电功率；PSTC是光伏面板在标准环境下的额定功率；fPV是功率衰退系数；G(t)是时刻t的实际光照强度；GSTC是标准环境下的光照强度；αP是功率温度系数；Tc(t)和Tc,STC分别为时刻t的光伏面板温度和标准环境温度。

光伏面板温度Tc(t)可由式(2)计算：

Tc(t)=Tae(t)+λG(t)

(2)

式中：Tae(t)表示实际的环境温度；λ表示辐射温度系数，取0.025 6。

根据式(1)和式(2)可得到光伏系统的年小时出力情况，并将其作为氢储能优化配置的前置输入条件，用于判断发电侧功率与调度指令之间的大小关系及二者的差值。

1.1.2 风电功率模型

风电功率取决于发电机特性和轮毂高度处的风速，如式(3)所示：

(3)

式中：Pwt(t)是风电的实际功率；Pr是风机的额定功率；v(t)是轮毂高度处的实时风速；vr、vin、vout分别表示风机的额定风速、切入风速和切出风速。

一般而言，直接获取的风速是测风塔高度的风速，需要折算成轮毂高度处的风速，如式(4)所示：

(4)

式中：vref(t)为测风塔高度的风速；Hwt和Href分别为轮毂高度和测风塔高度；γ表示摩擦系数。

根据式(3)和式(4)可得到风电的年小时出力情况，并将其作为氢储能优化配置的前置输入条件，用于判断发电侧功率与调度指令之间的大小关系及二者的差值。

1.1.3 氢储能功率模型

氢储存系统包括电解槽、储氢罐和燃料电池3种组件，如图1所示。电解槽单元利用电将水电解成氢气和氧气。目前，电解技术主要有3种：碱性电解水制氢、质子交换膜(proton exchange membrane,PEM)电解水制氢和固态氧化物(solid oxide electrolysis cell,SOEC)电解水制氢，其中碱性电解水制氢是最为成熟、产业化程度最高的制氢技术，因此本文采用该电解技术。理想状态下，ρ表示每kW·h电能通过电解槽电解所产生的氢气质量，η表示每kg氢气通过燃料电池燃烧所产生的电能。然而，实际中电解槽和燃料电池的转化效率远达不到100%，用θel和θfc分别表示电解槽和燃料电池的转化效率。

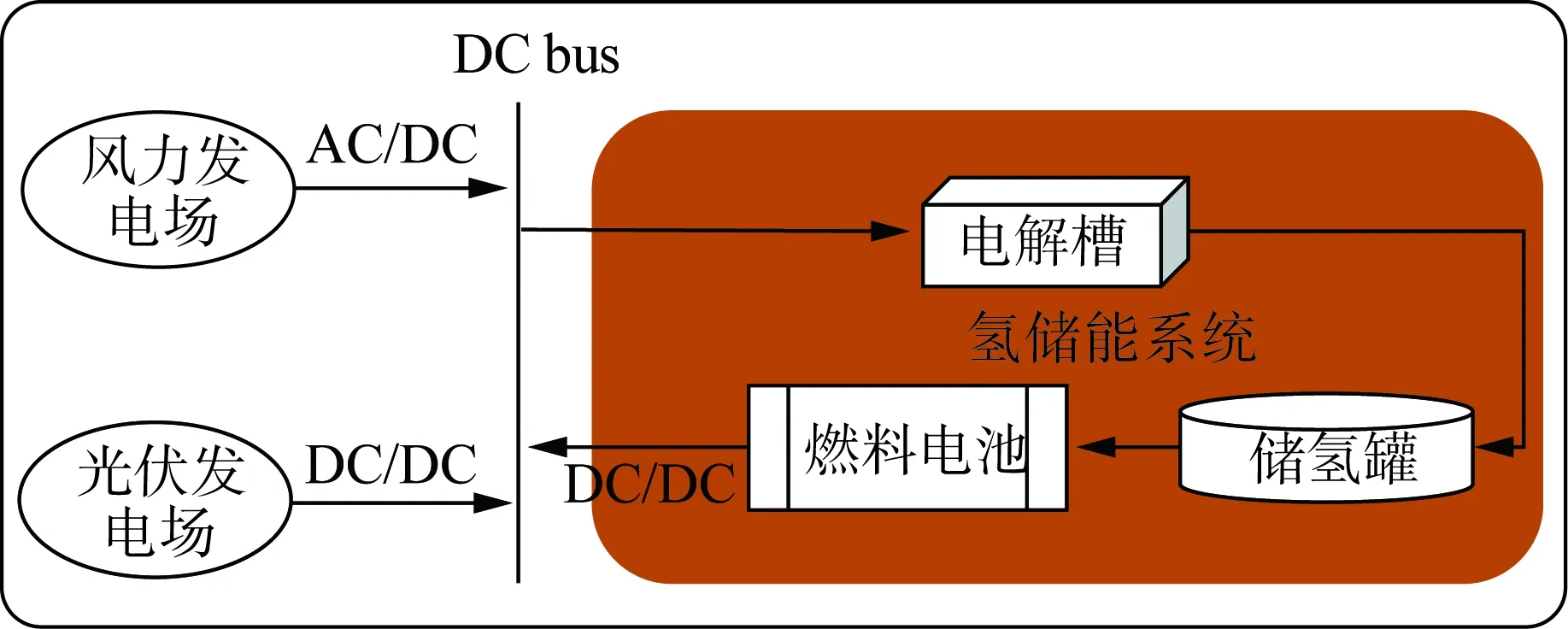
图1 氢储能系统示意图Fig.1 Diagram of hydrogen storage system

设在时刻t，风光发电功率之和为Pgen(t)，储氢罐容量为VSOC(t)。当新能源场站发电量大于调度指令时，将一定比例w的Pgen(t)通过电解槽电解，所产生的氢气储存在储氢罐中。此时，储氢罐容量的变化如式(5)所示：

VSOC(t)=VSOC(t-1)+Pgen(t)wρθel

(5)

当新能源场站发电量小于调度指令时，将一定比例ξ的VSOC(t-1)通过燃料电池产生电能。此时，储氢罐容量的变化如式(6)所示：

VSOC(t)=VSOC(t-1)-VSOC(t-1)ξηθfc

(6)

式(5)和式(6)分别表示电转氢和氢转电的情景，用于判断储氢罐中氢气的剩余容量，在氢储能优化配置中属于中间变量。

1.2 优化配置模型构建

1.2.1 决策变量

决策变量为电解槽、储氢罐和燃料电池的数量，用x1、x2、x3表示，为正整数变量。其中，单个电解槽和燃料电池的额定功率均为200 kW，单个储氢罐的额定质量为6 kg。

1.2.2 决策目标

本文考虑的决策目标包括初始投资成本、二氧化碳减排量增量和出力波动。其中初始投资成本和出力波动是成本型目标，其值越小越好；而二氧化碳减排量增量是效益型目标，其值越大越好。

目标1为氢储能系统的初始投资成本最低，如式(7)所示：

f1=min{CI,el+COM,el+CR,el+
CI,ht+COM,ht+CR,ht+CI,fc+
COM,fc+CR,fc}

(7)

式中：CI,el、CI,ht、CI,fc分别表示电解槽、储氢罐和燃料电池的设备初始购置成本；COM,el、COM,ht、COM,fc分别表示电解槽、储氢罐和燃料电池的设备总运维成本；CR,el、CR,ht、CR,fc分别表示电解槽、储氢罐和燃料电池的设备总替换成本。

CI,el=cI,elx1;CI,ht=cI,htx2;CI,fc=cI,fcx3

(8)

(9)

(10)

(11)

CR,el=cR,el∑[1/(1+r)]n，n=15

(12)

CR,fc=cR,fc∑[1/(1+r)]n，n=5,10,15

(13)

式中：cI,el、cI,ht和cI,fc分别表示单个电解槽、单个储氢罐和单个燃料电池的购买价格；cOM,el、cOM,ht和cOM,fc分别表示单个电解槽、单个储氢罐和单个燃料电池的年运维价格；cR,el、cR,ht和cR,fc分别表示单个电解槽、单个储氢罐和单个燃料电池的替换成本；r表示行业基准收益率，设定r=8%，将资金的时间价值考虑在内；n表示替换时间，由于新能源场站寿命周期为20年，而电解槽、储氢罐和燃料电池的寿命周期分别为15年、20年和5年，因此设定电解槽的替换时间为15，燃料电池的替换时间取值为5、10和15。

目标2为整个系统的二氧化碳减排量增量最大。氢储能系统的配置对清洁能源发电量所带来的增量属于无碳排电量，如果这部分电量借助当前电源结构发电，则会导致一定的二氧化碳排放。因此该目标计算如式(14)所示：

(14)

式中：决策单元以小时计算，一年时间设定h=8 760 h；Paf(t)表示配置储能后t时刻整个系统的出力；Pbe(t)表示配置储能前t时刻整个系统的出力；α表示每发1 kW·h电能的二氧化碳排放量，这里取0.96 kg(各种电力混合后的平均值，来源于中国生命周期基础数据库)。

目标3为整个系统出力与调度指令差值的波动最小(用方差表示)，如式(15)所示：

(15)

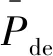
Pde(t)=Paf(t)-Pdof(t)

(16)

式中：Pdof(t)表示t时刻调度指令要求的功率。

1.2.3 约束条件

本文考虑的约束为弃电率约束和实际场地约束，如式(17)至式(20)所示：

Rpa≤θ

(17)

0≤Aelx1≤Ael,max

(18)

0≤Ahtx2≤Aht,max

(19)

0≤Afcx3≤Afc,max

(20)

式中：Rpa表示弃电率；θ为弃电率阈值，本文取30%；Ael、Aht和Afc分别表示单个电解槽、单个储氢罐和单个燃料电池的占地面积；Ael,max、Aht,max和Afc,max分别表示电解槽、储氢罐和燃料电池的可用占地面积。

2 求解算法

2.1 带精英策略的非支配排序遗传算法

1995年，Srinivas和Deb提出了非支配排序遗传算法(non-dominated sorting genetic algorithms，NSGA)，尽管该算法在许多优化问题上得到了应用，但它仍存在一些缺陷：1)计算复杂度较高；2)没有精英策略；3)需要人为指定共享半径。针对以上的缺陷，2000年Deb又提出了NSGA-II[20]。

NSGA-II算法的基本思想为：1)随机产生规模为N的初始种群，非支配排序后通过选择、交叉、变异操作得到第一代子代种群；2)从第二代开始，将父代种群与子代种群合并，进行快速非支配排序，同时对每个非支配层中的个体进行拥挤度计算，根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群；3)通过遗传算法的基本操作产生新的子代种群，依此类推，直到满足程序结束的条件[21]。相应的NSGA-II算法程序流程如图2所示。

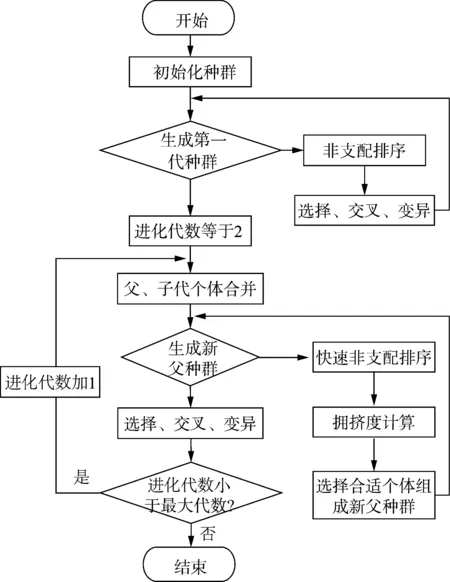
图2 NSGA-II算法基本流程Fig.2 Basic process of NSGA-II

2.2 熵权法

熵权法的基本思路是根据指标在各方案变异性的大小来确定指标的客观权重。假定有n1个方案，m个指标，xij表示第i个方案的第j个指标的数值。熵权法的计算步骤如下。

步骤一：数据归一化处理。设对各指标数据归一化后的值为yij，当指标为效益型时，有：

(21)

当指标为成本型时，有：

(22)

步骤二：计算第j项指标下第个i方案值占该指标的比重pij：

(23)

步骤三：计算第j个指标的熵值ej：

(24)

步骤四：计算信息熵冗余度dj：

dj=1-ej

(25)

步骤五：计算各项指标的权重wj：

(26)

式(21)至式(26)是对NSGA-II求解出的帕累托(Pareto)解的权重进行计算，从而结合各Pareto解的目标值对Pareto解进行大小排序。

3 研究区域

本文以甘肃省嘉峪关市的某风光场站为例进行分析，其中集中式光伏电场装机为200 MW，集中式风电场装机为400 MW。该地区的光照强度、风速及温度的年小时数据如图3所示。

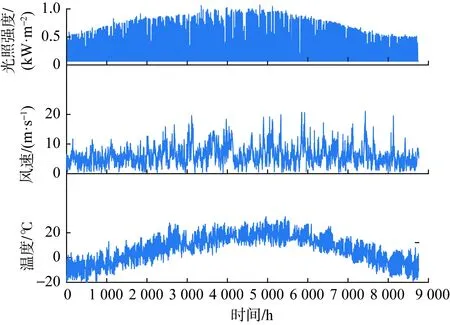
图3 嘉峪关市光照强度、风速及温度年小时数据Fig.3 Hourly data of radiation intensity,wind speed and temperature in Jiayuguan

光伏系统、风电系统及氢储能系统的相关参数取值分别如表1—3所示。氢储能系统成本相关参数取值如表4所示。

表1 光伏系统相关参数取值Table 1 Relevant parameters of photovoltaic system

表2 风电系统相关参数取值Table 2 Relevant parameters of wind power system

表3 氢储能系统相关参数取值Table 3 Relevant parameters of hydrogen energy storage system

表4 氢储能系统成本相关参数取值Table 4 Relevant cost parameters of hydrogen energy storage system

根据式(1)—(2)及表1中的数据，可以测算出该光伏电场的年小时出力；同理，根据式(3)—(4)及表2中的数据，可以测算出该风电场的年小时出力。风光电站联合出力和电网公司给出的调度指令如图4所示。

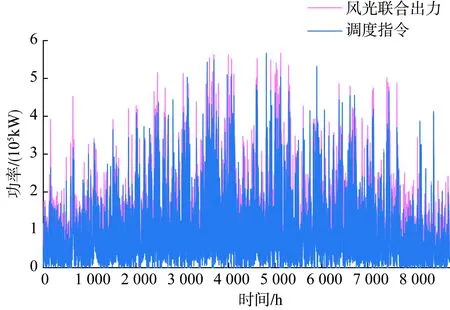
图4 风光联合出力和电网调度指令曲线Fig.4 Profile of wind and solar joint output and power grid dispatching instructions

4 优化配置结果及分析

本文采用NSGA-II算法对所构建的模型进行求解，参数设置如下：种群个数为100；遗传代数为500；交叉概率为0.9；变异系数为0.1。氢储能系统容量配置帕累托解结果如图5所示。

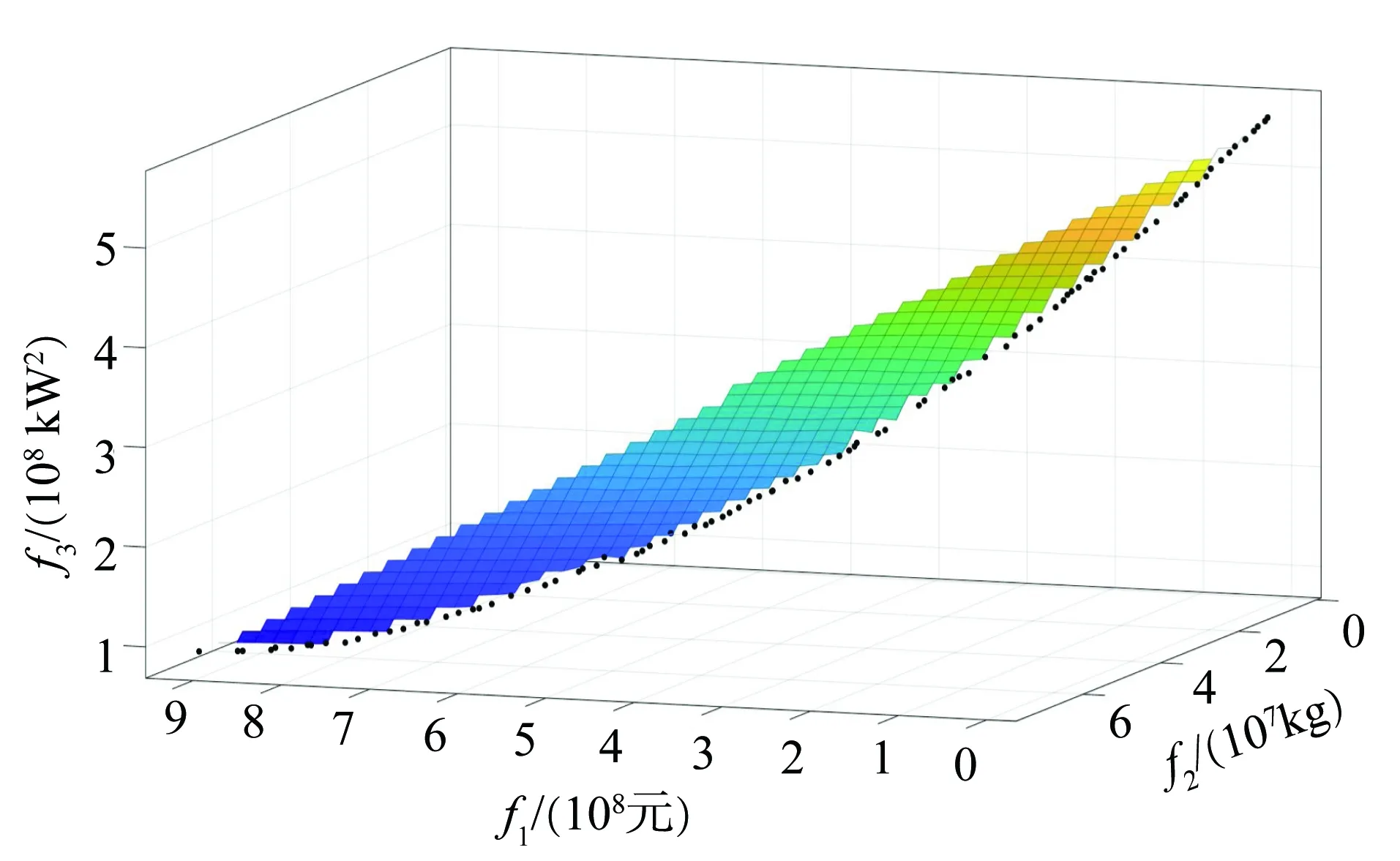
图5 氢储能系统容量配置帕累托解结果Fig.5 Pareto results of hydrogen storage system configuration

随后，采用熵权法计算出3个目标的权重分别为：0.408、0.241、0.351。在该结果的基础上，采用加权平均的方式可对已得到100个帕累托解进行排序，前五的折衷解配置结果如表5所示。可以看出，这5个解之间都是非支配占优的，即不存在一个解在3个目标上同时最优。

在氢储能系统配置前，全年整个系统出力与调度指令的方差(即目标3)为3.528×109kW2，而排序第1的配置方案的目标3值仅为该值的1.232%，波动明显减小。此外，氢储能系统配置前的年弃电量为3.668×108kW·h，而配置后仅为2.341×105kW·h，弃电量大幅度减少。为更加形象，随机抽取第124～459 h(2周共336 h)的储能配置前后各小时出力与调度指令的差值进行对比，结果如图6所示。可以看出，配置氢储能后的风光场站出力与调度指令基本吻合，并积极响应了调度指令。

表5 前五的氢储能配置结果Table 5 Top 5 configuration result of hydrogen storage system

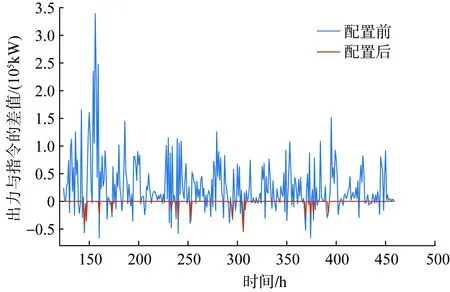
图6 配置前后的系统跟踪计划误差Fig.6 System tracking plan error before and after configuration

图7—9展示了两两目标间的关系。可以看出，目标1和目标2呈现正相关关系，这是因为氢储能系统的初始投资成本越大，则各组件的配置越高，新能源利用率越大，碳减排增量也相应增加。而目标1和目标3、目标2和目标3呈现负相关关系，其中目标2和目标3的负相关关系十分严格。这是因为氢储能系统的配置越高，系统出力与调度指令差值的波动性越小。

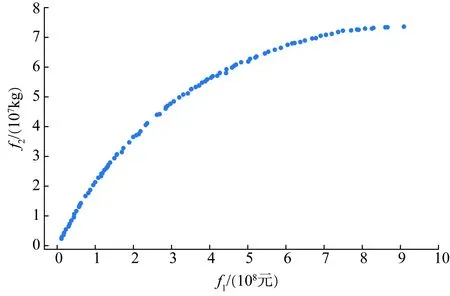
图7 目标f1和f2的相关关系Fig.7 Correlation between goals f1 and f2

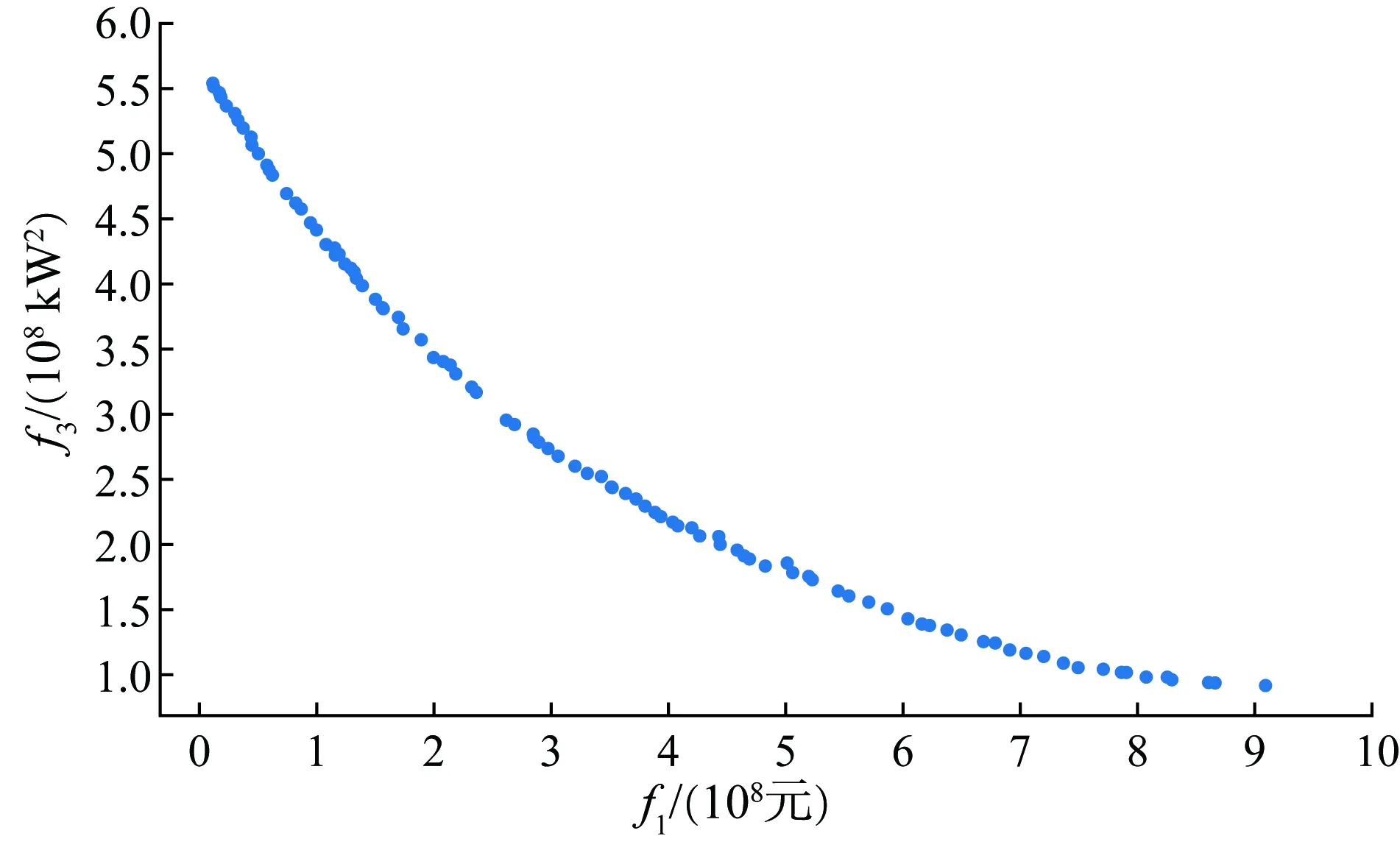
图8 目标f1和f3的相关关系Fig.8 Correlation between goals f1 and f3

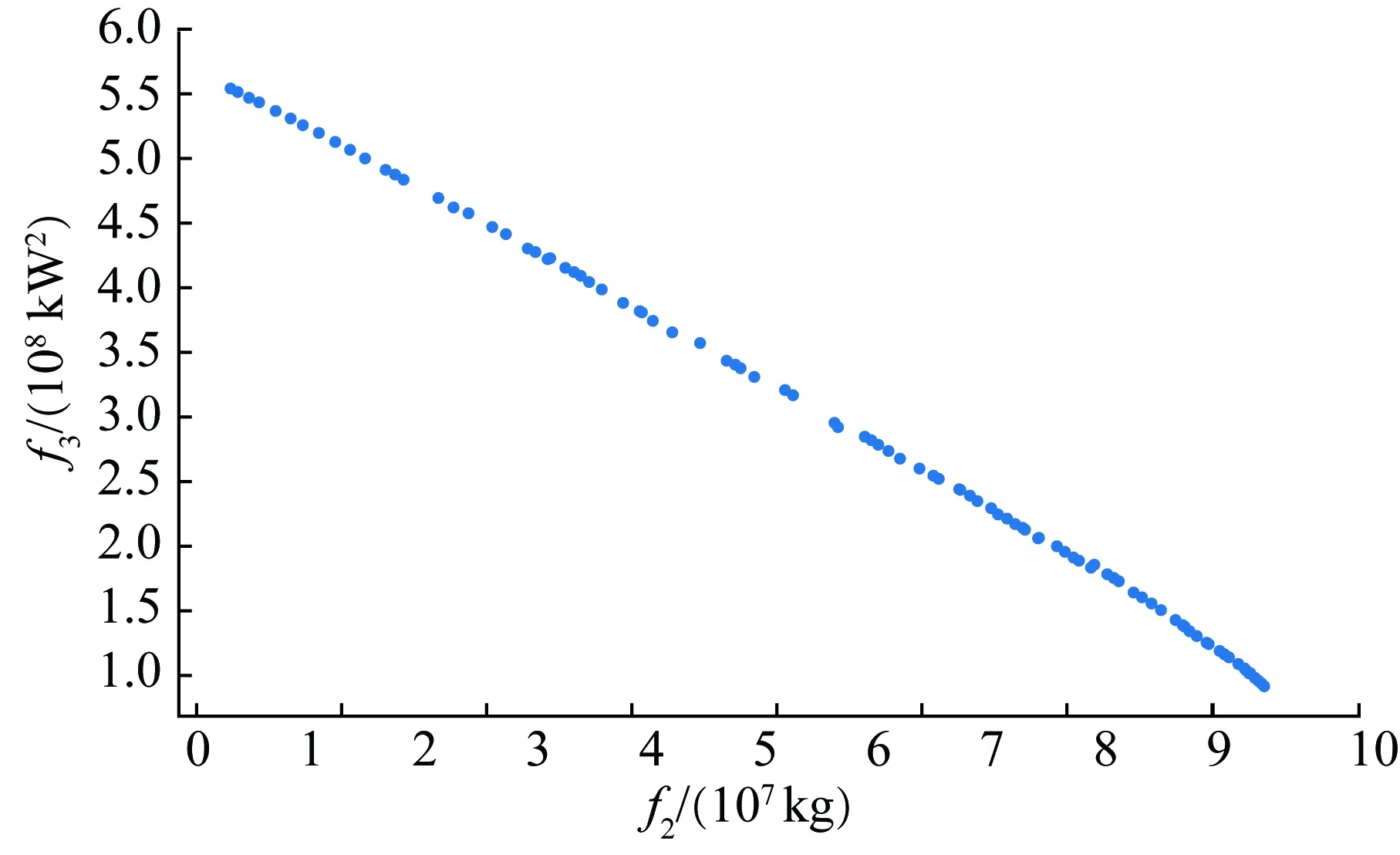
图9 目标f2和f3的相关关系Fig.9 Correlation between goals f2 and f3

仅从经济角度考虑，排序第1的配置方案配备氢储能系统后在30年全寿命周期中可以累计增加4.117×107kW·h的上网电量，其中风电增加2.386×107kW·h、光伏增加1.731×107kW·h。甘肃省嘉峪关市的风资源属于II类区域、光资源属于I类资源区，根据国家发改委最新发布《国家发展改革委关于完善风电上网电价政策的通知》和《光伏发电上网电价政策有关事项的通知》，该区域风电和光伏的上网电价分别为0.34和0.35元/(kW·h)。因此，配备氢储能系统可以增加额外上网电量收益1.417×107元。与此同时，在系统全寿命周期中可以累计多减排1.173×106t二氧化碳，按全国首笔碳配额交易价格(52.78元/t)核算，可带来约6.191×107元的收益。但相比于2.604×108元的氢储能总投资成本而言，上述两项收益之和只能回收约30%的成本，仍不具备商业化水平。因此，建议现阶段先进行小规模的应用示范，待氢能系统技术研发水平成熟时再逐渐推广。如果碳配额交易价格上涨至210元/t时，配备氢储能系统的额外收益将与氢储能系统投资成本相持平。

5 结 论

发展电氢耦合的氢储能系统是解决风光场站可再生能源消纳的有效途径。因此，本文针对发电侧新能源场站的氢储能容量优化配置问题，以氢储能投资成本最小、系统累计跟踪计划误差最小和二氧化碳减排量增量最大为目标函数，以弃电率和场地面积为约束条件，构建氢储能优化配置模型，并采用带精英策略的非支配排序的遗传算法、熵权法和加权平均法对模型进行求解。结果显示，面向200 MW集中式光伏电场和400 MW集中式风电场，电解槽、储氢罐及燃料电池的最佳配置数量分别为268个、291个和222个，容量分别为53.6 MW、1 746 kg、44.4 MW。本文的主要结论如下：

1)所构建的氢储能容量配置模型综合考虑了初始投资成本、二氧化碳减排量增量和系统累计跟踪计算误差三个目标。相比于现有仅考虑投资成本和出力波动的研究更为全面，充分响应了国家碳中和号召，所得优化结果更符合实际情景。

2)所构建的氢储能系统在全寿命周期内能减少1.173×106t的二氧化碳排放，按照标准煤碳排放系数0.68(来自于国家发改委能源所)测算，相当于节约了1.725×106t标准煤。

3)从氢储能配置前后对比来看，配置后整个系统出力与调度指令的方差为配置前的1.232%，波动明显减小；配置后整个系统弃电量仅为配置前的6.4%，弃电量同样大幅度减少。

4)现阶段，我国氢储能系统成本较高，尚不具备商业化水平。氢储能系统带来的综合收益之和只能回收投资成本的约30%。但若碳配额交易价格上涨到210元/t时，配备氢储能系统的额外收益将与氢储能系统投资成本相持平。此外，未来随着技术进步和规模化发展，氢储能系统的成本将大幅下降，商业化进程加速。

随着共享储能的商业模式日渐成熟，未来将进一步探索发电侧共享氢储能的容量配置问题。本文的研究对氢储能这一新型储能形态的应用示范提供了重要参考。