超图上最小边覆盖问题的算法研究

林雯 王嘉宝 陈智斌

(昆明理工大学理学院,昆明,650000)

1 引言

超图上最小边覆盖问题是一个NP难问题.首先我们引入超图的定义[1]:超图H=(V,E),其中V是一个有限集合,E是V的子集族,V中的元素称为超图H的顶点,E中的元素称为超图H的超边.给定边集C,C⊆E,若H中的任意一个顶点都在C的某条边内,则边集C称为一个边覆盖.在这种情况下,有时也称为边集C能覆盖H中的所有顶点.给定超图H,其中包含边数最少的边覆盖称为最小边覆盖.超图上最小边覆盖问题即求给定超图H上的最小边覆盖.超图上最小边覆盖问题等价于最小集合覆盖问题[2],最小集合覆盖问题在1972年首次由Karp[3]提出,因此一般可将求解最小集合覆盖问题的算法应用于超图上最小边覆盖问题.Crawford基于元启发式方法在2013年和2014年分别提出了人工蜂群算法和文化算法求解集合覆盖问题[4,5,6].2017年,Haddadi等对于该问题提出了分支定界法[7].以上方法在最坏情况下都是指数时间.虽然对于该问题无法求出精确解,但设计多项式时间近似算法得到问题近似解是可行的.Vazirani运用原始对偶模式给出了集合覆盖问题的f近似算法[8],其中f表示集合中最频繁元素的频数;同时,还提出了贪心算法求解该问题,达到Hs=1++···+的近似比,其中s表示集合的总个数.

以上问题可认为是不带权重的,本文考虑超图带权重版本,即上述问题的一个推广问题.假设H=(V,E)为一个超图,令w:E→Z+是一个权重函数,从而得到一个边赋权超图,记为Hw=(V,E;w).对任意的边集C⊆E,定义w(C)=w(e),即边集C在权重函数w下的权重.边赋权超图上的最小边覆盖问题即要求给定超图H=(V,E)在边赋权函数w:E→Z+下的一个边覆盖C,使得w(C)尽可能小.易知,超图上的最小边覆盖问题为边赋权超图上的最小边覆盖问题的一个特殊情况,即每条边权重均为1的情形.

本文首先针对边赋权超图最小边覆盖问题采用分层算法设计近似算法,达到f近似比.再对边赋权拉米纳超图,设计求解最小边覆盖问题的精确算法,首先构造对应的有根树[9],然后利用有根树的特殊性,基于动态规划的思想[10],对树从下往上按层次遍历各节点[11],求解出边赋权拉米纳超图上的最小边覆盖.

2 边赋权超图最小边覆盖问题

2.1 问题描述

考虑边赋权超图最小边覆盖问题,给定边赋权超图Hw=(V,E;w),w:E→Z+,其中V是一个有限集合,V中的元素v1,v2,···vn为超图Hw的n个顶点,E是V的子集族,E中的元素e1,e2,···em为超图Hw的m条超边.边赋权超图最小边覆盖问题是指找到图上的一个边集C⊆E,使得C能覆盖图Hw中的所有顶点,且w(C)=w(e)尽可能小.Hw中任何一个使得w(C)最小的边覆盖C称为最优边覆盖.若C∗为最优边覆盖,称w(C∗)为最优值,记为OPT(Hw)=w(C∗),简记为OPT,即OPT=min{w(C)|C为边赋权超图Hw=(V,E;w)的边覆盖}.

2.2 分层算法

利用分层算法求解边赋权超图最小边覆盖问题,其思想在于将超边集给定的权函数分解为关于超图的导出子图的一系列函数.首先,参照文献[8]中的表述,我们给出下面的定义和引理.

定义1给定边赋权超图Hw=(V,E;w),w:E→Z+,w(e)是关于超图Hw的边权重函数,若存在常数c＞0,使得w(e)=c·|e|,则称w(e)=c·|e|为边加权函数,其中|e|表示边e中的元素个数.

边加权函数在求解边赋权超图最小边覆盖问题中的重要性由下述引理可知.

引理1给定边赋权超图Hw=(V,E;w),w:E→Z+,若w(e)是超图的边加权函数,则w(E)≤f·OPT,其中f表示构成E的集合中出现最多次顶点的次数.

证明假设常数c满足w(e)=c·|e|,C∗是超图Hw的最优边覆盖,OPT是C∗对应的最优值.由于C∗覆盖Hw的所有顶点,故有

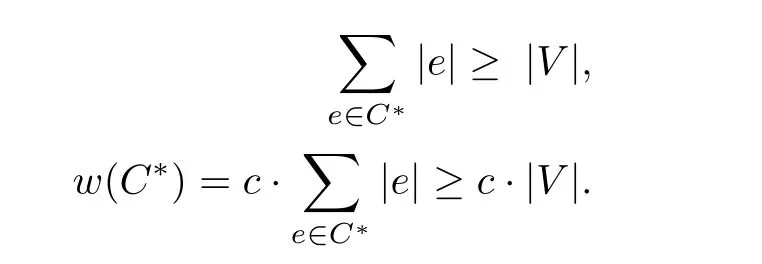
由每个顶点至多在f条边中,有

进而有

引理1得证.

定义2给定边赋权超图Hw=(V,E;w),w:E→Z+,从图中删除元素为空的边,然后在剩余边上计算c=min{w(e)/|e|},则称t(e)=c·|e|为最大边加权函数.称w′(e)=w(e)−t(e)为剩余权函数.

下面用分层算法在给定超图Hw上执行迭代.首先从图中删除元素为空的边,即|e|=0的边,然后在剩余边上计算c=min{w(e)/|e|},最大加权函数t(e)和剩余权函数w′(e).记D为元素为空的边集,W为剩余权为0的边集,P为包含集合D和W中顶点的点集.然后通过算法将超图Hw一层一层变成它原图的导出子图.

Algorithm1分层算法1:令Hw0(V0,E0)=Hw(V,E),C=∅,p=0 2:while Ep中存在元素非空的边do 3:计算cp=min{wp(e)/|e|p},tp(e)和w′p(e),将w′p(e)=0的边添加到Wp中;删除Ep的空边,将其原边添加到Dp中,将Wp与Dp的顶点添加到Pp中4:Hwp+1←Hwp[Ep−(Dp∪Wp)],Hwp+1为Hwp的导出子图,从Ep中删除Pp包含的顶点和Dp∪Wp包含的边,得到Ep+1,w′p+1(e)←w′p(e),|e|p+1←|e|p,p←p+1 5:end while 6:输出边覆盖C=r−1∪p=0 Wp

定理1分层算法是一个关于边赋权超图最小边覆盖问题的近似算法,近似比为f.

证明首先证明C是超图Hw的边覆盖.假设C不是Hw的边覆盖,那么C不能覆盖Hw的所有顶点,则至少有一个顶点在Dp中,这与Dp中只包含空边相矛盾.

再证明w(C)≤f·OPT.设C∗是最优边覆盖,考虑边e∈C,当p≤q时,若有e∈Wq(q=0,1,2,···,r−1),则可以将该边的权分解为余权函数为零的点集,最终得到超图的边覆盖为

同时考虑e∈E−C,若e∈Dq,则边e的权满足以下不等式,

其中OUT表示算法得到的输出值.定理得证.

2.3 紧例子

例1给定边赋权完全二部图Kf,f(见图1),其中有2f个顶点,f2条边,每条边上的权重均为1.分层算法选取图上f2条边作为输出解,OUT=f2,而最优解是边集{{v1,u1},{v2,u2},···,{vf,uf}},OPT=f,即OUT=f·OPT.

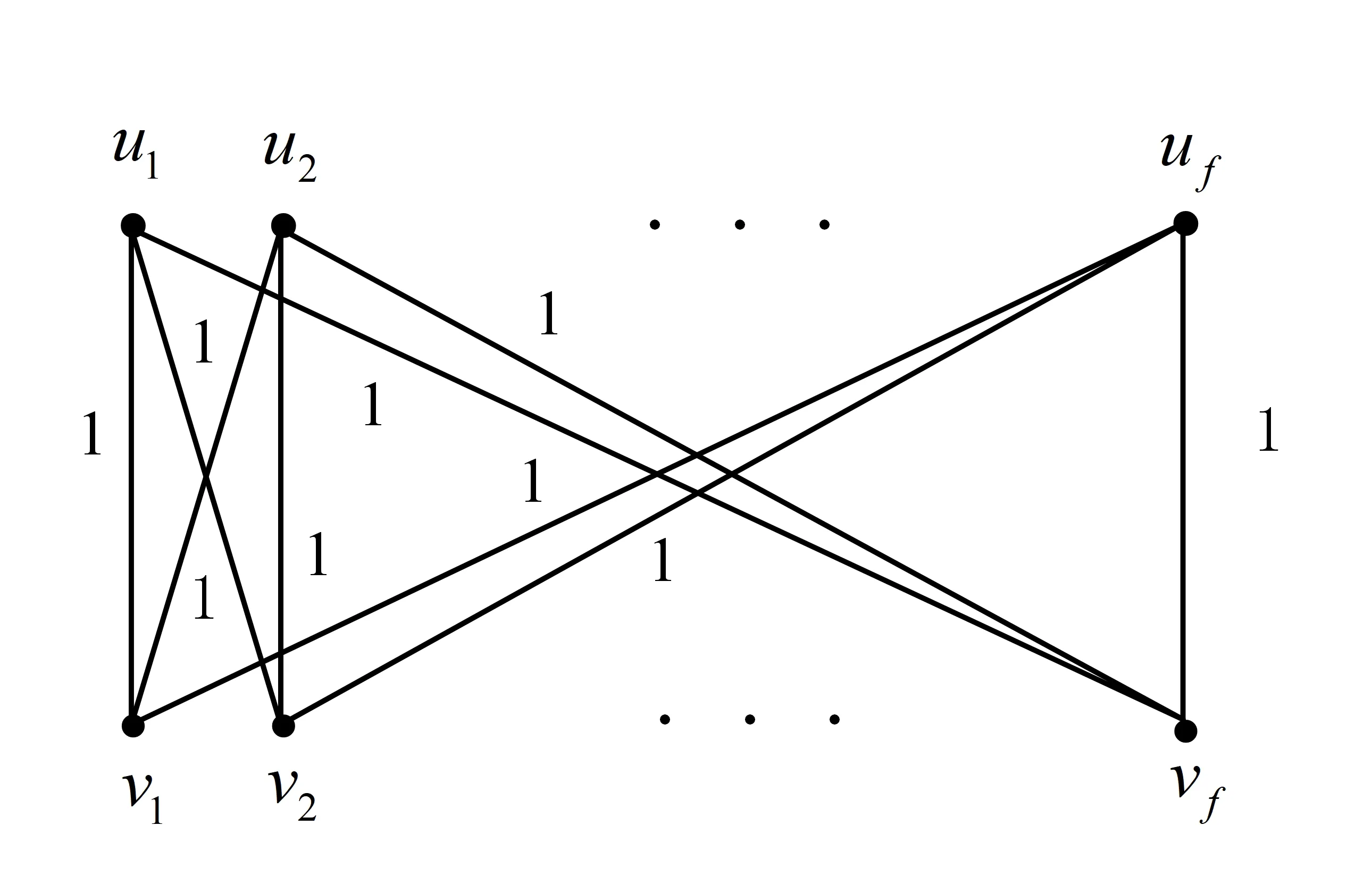
图1 边赋权完全二部图Kf,f

例2给定边赋权超图Hw,其中V={v1,v2,···,vn},E={{v1,v2,···,vf},{v2,v3,···,vf+1},···,{vn,v1,···,vf−1}},每条边包含f个顶点,每条边的权重均为1,分层算法选取图上所有边,OUT=n,而最优解C∗={{v1,v2,···,vf},{vf+1,vf+2,···,v2f},···,{vn−f+1,vn−f+2,···,vn}},OPT=n/f,即OUT=f·OPT.

3 边赋权拉米纳超图最小边覆盖问题

3.1 边赋权拉米纳超图

定义3([12])给定边赋权超图Hw=(V,E;w),w:E→Z+,其中n个顶点分别为v1,v2,···,vn,m条超边分别为e1,e2,···,em,若超图的边满足:ei∩ej=∅或ei⊆ej或ej⊆ei(i,j=1,2,···,m),则称该边赋权超图为边赋权拉米纳(Laminar)超图.

3.2 边赋权拉米纳超图最小边覆盖算法

3.2.1 构造有根树

为了构造有根树,我们先给出如下几个定义.

定义4([15])对于一颗有向树,若恰有一个顶点入度为0,其余顶点入度为1,则称此有向树为有根树.

定义5([16])如果一个集合ei中的每一个元素都在集合ek中,且ek中可能包含ei中没有的元素,则称ek为ei的一个超集.

现在针对拉米纳超图Hw=(V,E;w),w:E→Z+,介绍构造有根树T=(U,A;w)的方法.有根树的节点:(1)边集E中的每条超边ei作为节点;(2)在T中用e0表示V,e0作为根节点,树T的节点集为U=E∪e0.在树T中,对任意节点ei∈E,权重表示为wei,对于节点e0,令we0=+∞.

关于有根树T中的边集,我们有:(1)若ei在E−ei中无超集,则存在一条e0到ei的有向边(e0,ei).(2)若ei⊆ek,且不存在j∈{1,2,···m}{i,k}使得ei⊆ej⊆ek,则存在一条ek到ei的有向边(ek,ei)(k=1,2,···,m).则有根树T有m+1个节点,m条边,且根据拉米纳超图构造一个有根树T的时间复杂度是O(m2).由于有根树T满足偏序关系＜U,⊆＞,因此有根树T的构造与对应的哈斯图一致[13].有根树满足以下定理.

定理2([14])T是一个以e0为根节点的有根树,对任意ek∈E,在T中有且仅有一条从e0到ek的有向路,若ei⊆ek,则在T中有且仅有一条从ek到ei的有向路.

文献[14]通过构造集合覆盖对应的辅助网络,在辅助网络中求解s−t割,利用集合覆盖和割集的关系解决集合覆盖问题.本文在此基础上,构造边赋权拉米纳超图对应的有根树求解边赋权拉米纳超图最小边覆盖问题.

3.2.2 MEC算法和计算复杂性分析

基于拉米纳超图Hw构造对应的有根树T后,现在给出求解边赋权拉米纳超图的最小边覆盖问题的MEC算法.设L⊆{e0,e1,e2,···,em}是T的叶节点集合,对任意ei∈E,des(ei)表示节点ei的所有子节点以及后代节点的集合,pr(ei)表示节点ei的唯一父节点.

Algorithm2MEC算法1:构造一个关于拉米纳超图Hw的有根树T 2:记T的所有叶节点集合为L,C=∅3:if∪ek∈L ek=V then 4:C←L 5:else 6:记M=V− ∪ek∈L ek为缺失元素集合,在T上从e0遍历包含M中元素的节点ei,直到对∀x∈M,x/∈ei,则C←L−({ei}+des(ei))+{pr(ei)}7:end if 8:从L中的节点开始从下往上层次遍历T中节点直到e0,9:if wei≤ ∑wej then 10:C←C−{ej}+{ei}11:end if 12:输出C为Hw的最小边覆盖.ej∈C∩des(ei)

定理3MEC算法输出的C为拉米纳超图Hw的最小边覆盖.

首先构造一个有根树的时间复杂度为O(m2),利用MEC算法找边赋权拉米纳超图的最小边覆盖,算法第2 11步的时间复杂度是O(m3),即MEC算法时间复杂度O(m3),所以求解拉米纳超图上最小边覆盖问题的时间复杂度为O(m3).

3.2.3 一个实例

给定拉米纳超图Hw=(V,E;w),其中V={v1,v2,v3,v4,v5,v6,v7,v8,v9,v10,v11,v12},E={e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12}.

表1是上述拉米纳超图Hw的超边权值表,图2为Hw的形象化表示,图3是基于Hw构造的有根树T(U,A;w).运用算法2,第1步构造实例对应的有根树T,在第2 7步判断缺失顶点为v8,删除e8,得到当前边覆盖C={e9,e10,e7,e3,e11,e12,e5};第8 11步,在T中遍历所有节点,最终得到最小边覆盖C={e9,e10,e7,e3,e1},对应权重w={1,2,1,1,4},最小边覆盖的权重和为9.

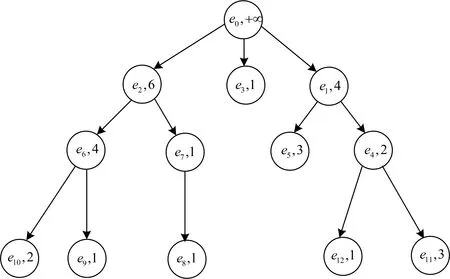
图3 拉米纳超图Hw的有根树T

表1 拉米纳超图Hw边权表

图2 拉米纳超图Hw

4 总结

求边赋权超图最小边覆盖问题是NP难的,但在拉米纳超图上,求解边赋权最小边覆盖问题是多项式时间可解的.本文首先针对边赋权超图最小边覆盖问题设计了分层算法,通过该算法将超图分解为一系列导出子图,根据每层子图的构造,取每层子图上的特定集合的并为最小边覆盖.设计的分层算法达到f近似比,时间复杂度为O(rm),并给出了该算法的紧例子.其次针对边赋权拉米纳超图最小边覆盖问题设计MEC算法,根据拉米纳超图中边的关系构造有根树,然后基于动态规划的思想,按树的层次遍历树中的节点,最后求得边赋权拉米纳超图的最小边覆盖.MEC算法的时间复杂度为O(m3).