基于SQP算法的银行贷款组合优化

顾安琪刘文鼎刘培江王浩华,4,

(1.海南大学理学院数学系,海口,570228;2.海南大学计算机与网络空间安全学院,海口,570228;3.广东财经大学统计与数学学院,广州,510320;4.海南大学海南省工程建模与统计计算重点实验室,海口,570228)

1 引言

贷款作为商业银行主要的盈利手段,对银行的生存与发展具有十分重要的意义,而贷款配置的合理性作为贷款收入的决定性因素,引发了大量的研究[1].Bodnar等在利率服从正态分布的情况下使用贝叶斯估计法,计算了最小标准差贷款组合的权重.但在实际情况中,贷款收益率更多地呈现出不符合正态分布的特性[2].徐绪松等在非正态稳定分布的条件下建立了均值 尺度参数投资组合模型,更加严格地控制了资产配置的风险[3].迟国泰等以稳定分布为基础,提出了考虑存量贷款的多目标优化模型,不仅降低了模型的评估风险,而且实现了对偏度的控制,增加了收益[1].显然,存量贷款的比重对实际投资决策具有直接影响.

本文引入风险集中度,以此控制存量贷款的集中程度,降低贷款组合因过度集中而导致的额外风险,构建基于存量贷款分配比例下的银行贷款组合优化模型.在此基础上,通过对目标函数的改进,使目标函数在兼顾收益、偏度、尺度的同时,考虑银行自身的偏好,并减少变量的个数,最终转化为求解一个非线性规划问题.为了简化计算,得到收敛性更高的结果,本文使用SQP算法来求得最终的分配比例.实证研究表明,此模型具有可行性与合理性,符合银行对高利润与低风险的预期,且便于理解与操作.

2 基于稳定分布的全部贷款目标分析

在实际市场中,贷款收益率往往无法通过正态检验,其经验分布明显不具有稳态、峰度等正态特征[3].此时使用正态分布模拟收益率的分布,会导致模型误差较大.徐绪松等的研究表明贷款收益率服从非正态稳定分布.

设rit(i=1,2,···,N;t=1,2,···,T)为第i笔贷款第t个月的收益率;RN为贷款组合收益率,ai为常数,bi为中国债券指数被第i笔贷款的影响程度;rMt(t=1,2,···,T)为中国债券指数在第t个月的收益率,εit为第i笔贷款在第t个月收益率的随机误差,RN为投资组合收益率,N为总贷款数量;wi为关于第i笔贷款总额的份额.参考文献[3]中给出了如下的市场经济模型

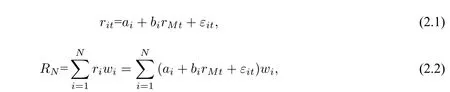
其中,第i笔投资服从稳定分布,即ri∼S(αi,βi,γi,δi),αi∈[0,2]为特征指数,用以描述投资收益率尖峰度和厚尾度,αi越大尾部越薄、峰度越小;βi∈[−1,1]为偏斜程度指数,用以表现投资利率相较于均值的偏离状态,βi＞0时分布向右移动,βi＜0时分布向左移动;γi＞0为尺度参数,表示分布偏离其均值的离散状态;位置参数δi∈R表示平均值所在的方位.

每笔贷款的收益率受中国债券指数和随机因素扰动的影响.由于第i笔贷款的收益率ri服从稳定分布,因此,根据市场经济模型（2.2）计算出的投资组合回报率也服从稳定分布,从而得出贷款组合尺度参数如下[3]:

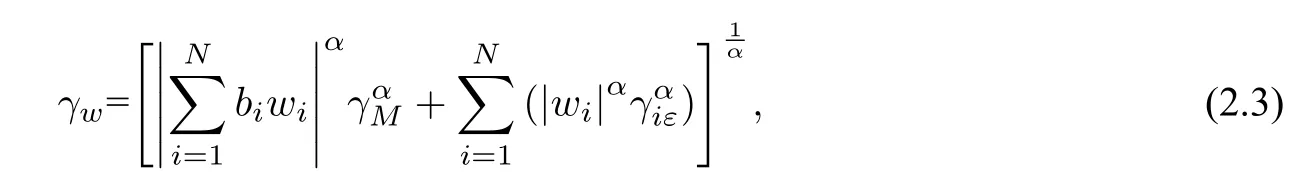
其中,γw为贷款组合尺度参数;γw为投资组合的尺度参数;α为中国债券指数的特征指数;γM为中国债券指数的尺度参数;γiε为第i笔贷款随机误差的尺度参数.

贷款组合的尺度参数γw显示了贷款组合收益率与均值的拟合程度.γw越大则投资组合回报率分布与均值离散程度越高,投资组合风险也越大.因此,定义投资组合的偏斜指数

其中,βM为中国债券指数的偏斜指数;βiε为第i笔贷款随机误差的偏斜指数.

3 全部贷款的组合优化模型

现有的多目标全部投资组合优化模型兼顾贷款组合的回报、尺度参数与偏斜参数,具有多个目标函数,求解困难.改进后的全部贷款组合优化模型将多个目标转化为单目标,在实现收益最大化,风险最小化的同时考虑到了银行自身的风险偏好.所建立的单目标函数如下:

其中,Rn+m为全部贷款组合的收益率;n为存量贷款的笔数;m为増量贷款的笔数;wi第i笔贷款全部贷款总额的份额;为第i笔投资收益率的均值;γn+m为全部贷款组合的尺度参数;βn+m为全部贷款组合偏斜指数.

在实际市场中,收益率服从非正态稳定分布,能够很好地描述收益率的经验分布所具有的差异性和不足性特征,可以更高效地管控投资组合的风险[1].偏斜指数代表分布偏离均值的离散程度,βn+m越大,超额收益越多;λ1越小,则代表银行对投资组合回报率的偏好越大;λ2越大,则银行对投资组合尺度参数的偏好越大;λ3越小,表明银行对投资组合偏度的偏好越大（βn+m＜0时,λ3应取负数,βn+m＞0时λ3取正数）.银行可根据自身风险偏好与承受能力自行调节比例.本模型综合贷款组合收益率、尺度参数与偏斜指数作为目标函数,实现了多个目标向单一目标的变换,克服了多目标函数难以求解的问题,同时考虑了投资方对风险与收益的偏好程度,相较于现有模型的目标函数,形式更加简洁,计算更加简便,也便于理解,且在稳定分布的基础上,考虑通过最大化贷款系数来检验贷款组合方案的正确配置,从而可增加高于平均收益率的可能性,提高贷款的剩余收益率,弥补现有稳定利率研究中忽视潜在收益的资产分配.

对所有权重wi进行归一化后,我们有

由于单项投资占总投资的比能反映投资的集中度大小,因此引入风险集中度L,令

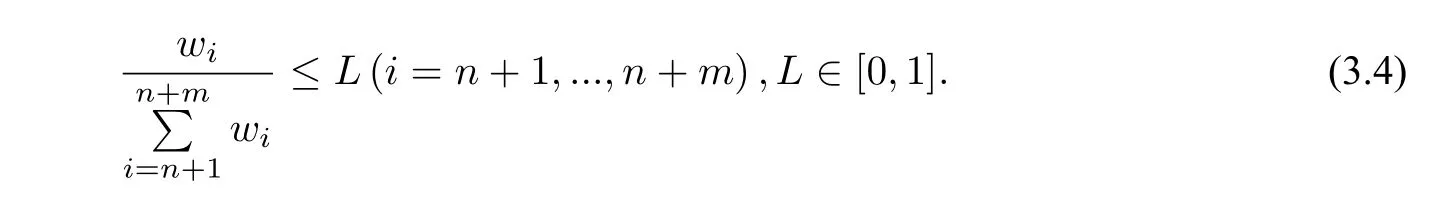
若增量贷款的分配过于集中,则会导致企业风险转嫁至银行,因此引入风险集中度控制各笔增量贷款在总增量贷款中所占的比例来分散风险,保证贷款收益的稳定性.

以式(3.1 )为目标函数,(3.2 ),(3.3 ),(3.4 )为约束条件,建立如下的新的全部贷款组合优化模型:

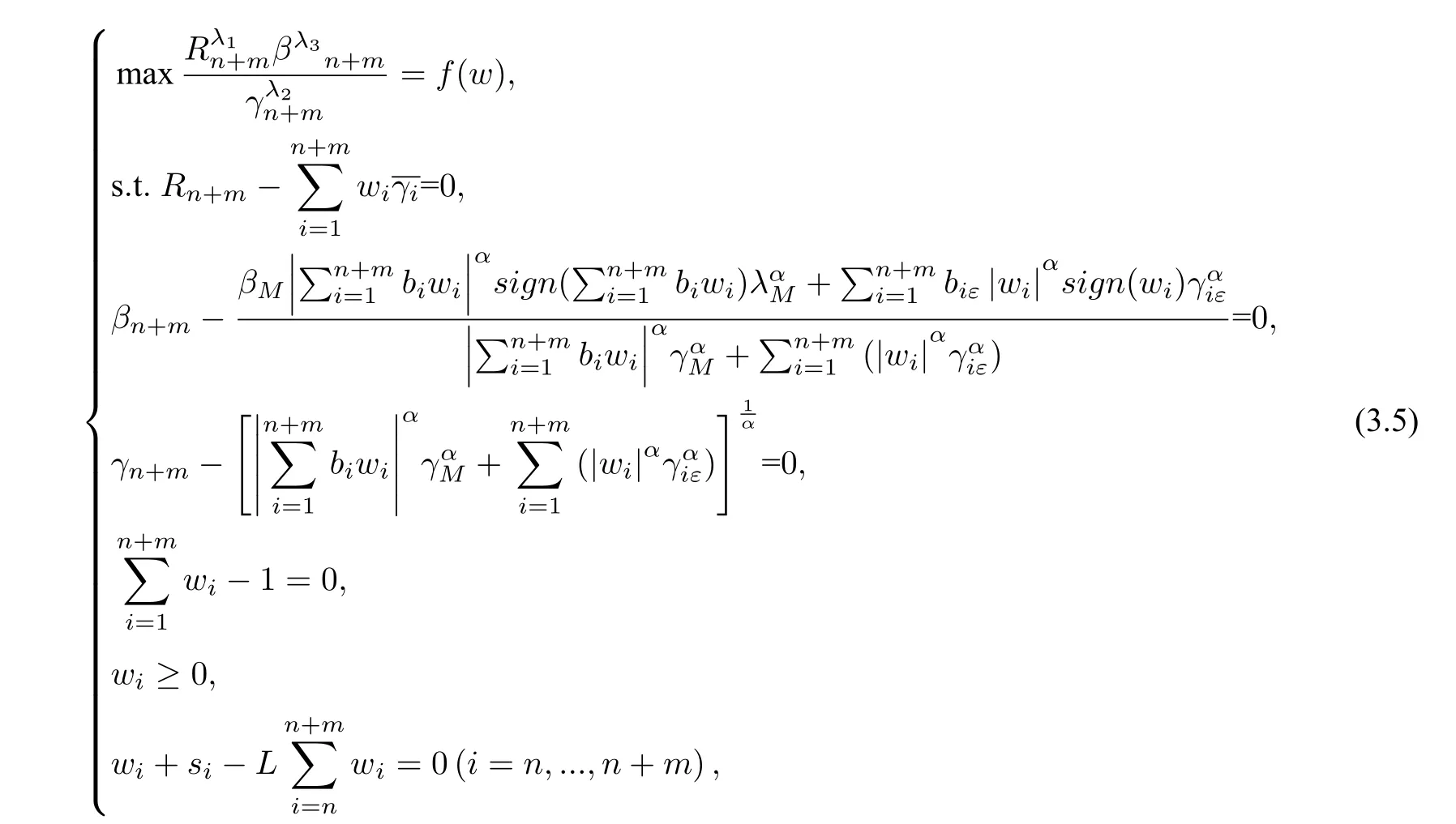
其中wi,i=n,...,n+m为待定的决策变量,si为剩余变量.

上述模型对贷款收益率、贷款尺度参数以及偏斜指数的计算分为存量贷款与增量贷款两个部分,考虑到了现有贷款对贷款组合收益与风险的影响,防止了n笔存量贷款可能引发巨大损失.目标函数由贷款收益率、尺度参数、偏度参数组成,保证了在贷款收益率最大的情况下,偏斜指数最大的同时,尺度参数最小,即收益最大的同时,风险最小.该模型相较于现有模型,变量个数大幅减少,易于后期计算与求解,同时权重指数的添加避免了在现有的投资组合优化研究中缺乏主观收益的问题[3−7].

4 基于SQP技术的算法框架

SQP算法优点在于具有超线性收敛速度并且函数求值、梯度求值的次数少.因此这里采用matlab中的序列二次规划算法（SQP）求解:将最优解问题转化为一系列的二次规划子问题,对拉格朗日函数进行两次逼近,提高二次规划子问题的逼近性;用拟牛顿法求出Hessian矩阵,给出Hessian矩阵（或其逆矩阵）的两个迭代公式:BFS公式和DFP公式[8].步骤如下:

Step1更新拉格朗日函数的Hessian矩阵.在每次迭代中,使用BFGS法求解Lagrange函数的Hessian矩阵的正定近似值H.在此过程中需保持Hessian矩阵正定.

Step2二次规划子问题求解.求解过程分为两个阶段:首先计算解的可行点;然后生成与问题解相吻合的可行点的迭代序列,由这个序列收敛得到问题的解.

Step3一维搜索和目标函数计算.通过求解子集问题得到向量,并由此得到一个新的迭代(迭代过程中应充分减小目标函数的值).

在实际求解的时候,将目标函数转化为其相反数并求最小值,将SQP方法中的l1罚函数推广为lp罚函数[9],该搜索方向是lp罚函数在原问题的解的迭代的下降方向.

假设:

（A1）目标函数f(w),约束条件ci(w),i∈I0是二阶连续可微函数;

（A2）Lagrange函数的Hessian矩阵的近似矩阵Hk是正定的,并且存在两个正数m和M使得

对一切的k≥1和d∈Rn都成立.

引理1([9])设w∗∈S为(NLP)问题的局部极小点,f(w),ci(w)(i=1,2,···,m)在w∗处连续可微,且∇ci(w)(i∈A(w∗))线性无关,则存在实数λi(i∈I),uj(j∈E),使得

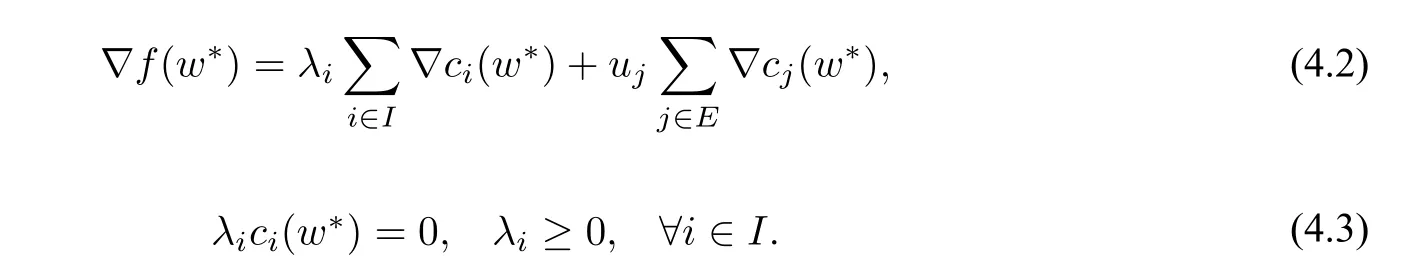
注(4.2 )与(4.3 )称为Kuhn Tucker条件,简称K T条件,满足(4.2 )与(4.3 )的点称为K T点.

定义函数θ(w,r)=g(w)T d+r∆(w).如果w是非线性规划问题的一个K T点,则对任意的r∈R,有θ(w,r)=0,其中g(w)T为目标函数f(w)的拉格朗日算子矩阵转的置阵,d为Hk的过渡矩阵,r为任意实数,∆(w)为K T条件中的下降方向指示函数,当且仅当w为可行点时,∆(w)=0.

定理1在假设（A1）和（A2）下,若f(w)在Rn中有界,{wk}是SQP算法产生的无限序列,且罚函数{rk}有界,则{wk}的任意聚点都是此问题的K T点.

证明不失一般性,假设对所有的k,rk=r,且w∗是{wk}的一个聚点,则存在一个子集K,使得当k→∝(k∈K)时,wk→w∗.如果θ(w∗,r)=0,则由定理可知w∗是此问题的K T点.如果θ(w∗,r)＜0.则存在−k,使得对一切k≥−k(k∈K),都有

由引理1 可知

dk→0,k→∝(k∈K).

所以

θ(wk,r)→0,k→∝(k∈K),

与(4.4 )式矛盾,因此θ(w∗,r)=0,即w∗是此问题的K T点.

计算时,目标函数满足假设(A1),(A2),且在Rn内有界.又因为罚函数lp有界,解序列{wk}是无限的,故{wk}的任何聚点都为此问题的K T点[10],且解空间为凸集,极值点为最优解.

综上所述,使用SQP算法对目标函数进行分析时,只要满足（A1）与（A2）两个条件,就能通过迭代得到K T点,因此,SQP算法在这样的条件下是收敛的.在解决全部贷款的组合优化问题时,改进的全部贷款组合优化模型(3.5)显然其目标函数及约束条件是二阶连续可微的,且Hk满足（A2）条件,故改进的全部贷款组合优化模型问题在运用SQP算法进行迭代计算时是收敛的,从而可用SQP算法在matlab程序中进行计算.

5 实证分析

参考文献[1]中收集了某银行贷款近4个月的数据:贷款总额为1000亿元,其中现有的9笔贷款总额为750亿元,每笔现有贷款金额及占贷款总额的比例见表1.表2前十三行给出了“增量”和“存量”的所有贷款收益率信息,中国债券指数收益率见表2第14行[1].

表1 存量贷款信息[1]

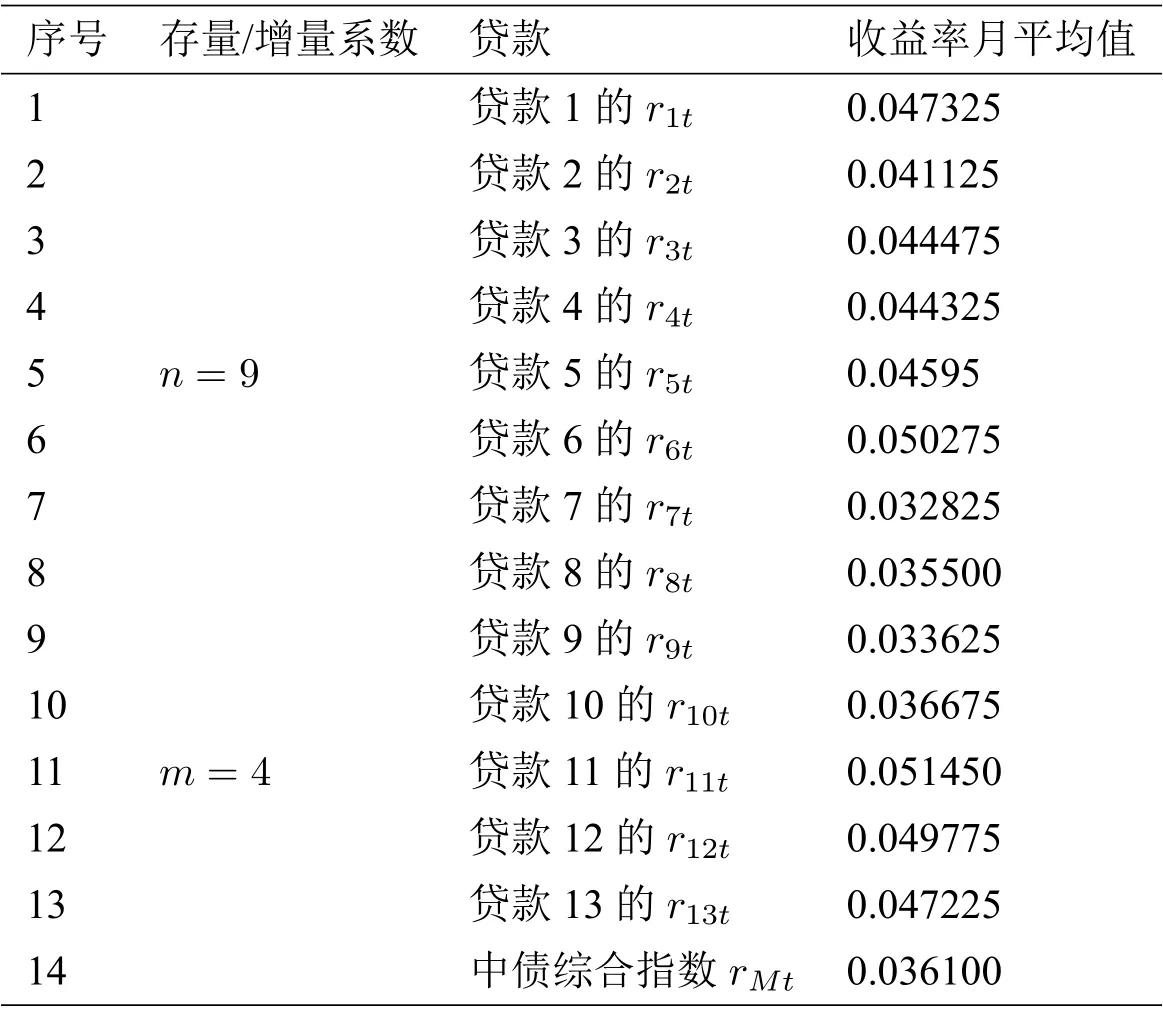
表2 收益率信息[1]

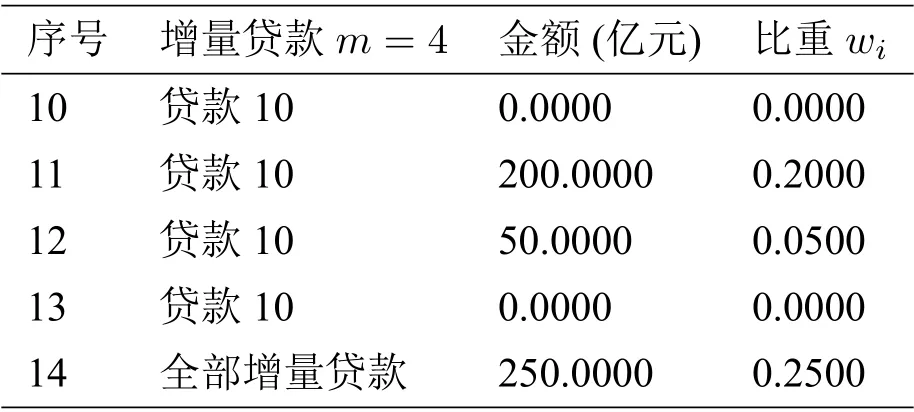
表3 增量贷款信息

将模型(3.5 )的各参数分别代入基于稳定分布的多目标全部贷款组合优化模型[1](以下简称为现有模型)进行实验,通过matlab程序实现得到的对比结果见表4.

表4 各特征参数对比结果

6 结论

将现有模型与本文的模型(3.5 )进行对比,模型(3.5 )的收益率Rm+n=0.0447 与现有模型的收益率Rm+n=0.0447 一致,符合银行对高效益的预期;模型(3.5 )的全部贷款组合偏斜指数βm+n=－0.0216 与现有模型的对应数据βm+n=－0.0216 相同,超额收益得到保障,本文模型中的全部贷款组合尺度参数γm+n=0.0883 ,与现有模型的尺度参数γm+n=0.0882 基本一致,有效地控制了贷款组合的风险,且目标函数的形式更加简洁,变量大幅减少,易于求解.模型(3.5)加入了对存量贷款的考虑,从表1能够看出全部存量贷款在各个贷款中金额的合理分配,能够有效降低存量贷款被忽略所带来的风险.本文提出的模型(3.5)实现了控制风险,追求风险与利润并重的目的,计算上具有简易性与可操作性,并且使用SQP算法对问题进行求解,收敛性好,结果较为准确.模型(3.5)引入风险集中度,较现有模型大大减小了投资过于集中所带来的风险,贷款结构更加合理可控且组合收益率较大.以稳定分布为基础的收益率模型,能够表达出收益率不对称性以及尖峰厚尾的性质,对组合风险管控更加精确有效且符合实际情况.