带时间依赖扩散系数的分数阶非经典扩散方程的适定性

刘迪 刘西盟 谢永钦

(长沙理工大学数学与统计学院,长沙,410001)

1 引言

本文考虑如下带有时间依赖扩散系数的分数阶非经典扩散方程的适定性问题:

其中Ω⊂Rn(n≥3)是一个带有光滑或分段光滑边界∂Ω的有界域,A:=−∆,θ∈(0,1],g∈L2(Ω)是已知函数,并且满足如下初边值条件

我们对方程(1.1)的非线性项和时间依赖的扩散系数做如下假设:

(H1)非线性项f∈C1,f(0)=0,且满足

这里αi,βi(i=1,2)和l均是正常数.

(H2)时间依赖的扩散系数ε(t)是非负递减的函数,满足

且存在常数L＞0,使得

当ε(t)≡1且θ=1时,(1.1)即为通常的非经典反应扩散方程,Aifantis在[1]中对其建立了一般的框架.非经典反应扩散方程一般用于描述非牛顿流体、固体力学和热传导等物理现象(见[2,3]).近三十年来,大量学者对非经典反应扩散方程解的存在性及其长时间行为进行了研究.特别是在方程(1.1)中,当θ=1,且系统带有粘性扰动项ε(t)Aut时,Zhu等在[5]中证明了方程的适定性及时间依赖空间全局吸引子的存在性.

近年来,关于分数阶偏微分方程亦有相关研究.特别是人们在研究介于理想固体和液体之间的复杂状态物质等大量的实际问题时,为了更精确地描述复杂介质的应力松弛的非指数型、有记忆性等应力应变关系,提出并建立了如下分数阶扩散方程([10]):

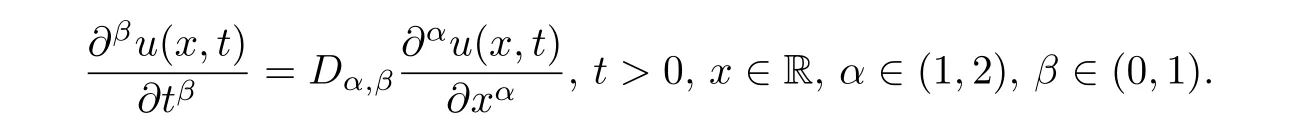
Saxena等在[4]中研究了如下分数阶反应扩散方程的适定性及相关问题:

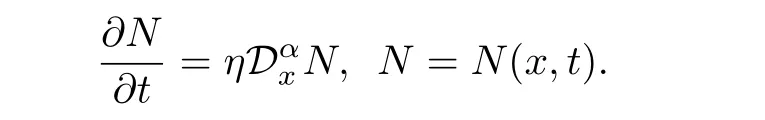
汪庆康在[9]中研究了分数阶拉普拉斯算子指数非线性热方程柯西问题的适定性.如果我们仿照[1]中建模的基本框架,然后考虑扩散系数并非常数而是时间依赖的函数时,则可得到本文所研究的方程(1.1).在[7]中,Wang等研究了当ε(t)≡1时的如下方程:

ut+(−∆)sut+(−∆)su+λu=f1(x,u)+f2(x,u)+g(t,x),x∈RN,

解的存在唯一性及其长时间行为.但对带有初边值条件(1.2 )的方程(1.1 )的适定性还未发现相关研究文献.

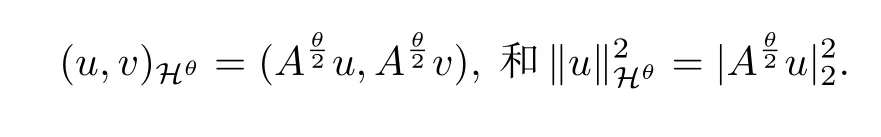
2 适定性

定义2.1 (弱解的定义)若u=u(x,t)满足

及对所有的φ∈C∞0(Ω),有

对t∈[τ,T]几乎处处成立,则称u为带有初边值条件(1.2 )的方程(1.1 )的弱解.

为了获得方程(1.1)整体弱解的存在性,根据Faedo Galerkin方法的基本思想,首先需构造问题(1.1 )–(1.2 )的Galerkin近似解.为此,令(x)是如下特征方程的特征函数

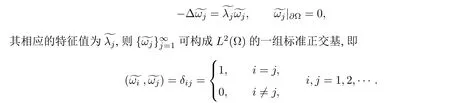
使其满足

由常微分方程理论,易知系统(2.2)存在唯一解.

2.1 先验估计

引理2.1 假设(H1)−(H2)成立,且um(t)是带有初值umτ的系统(2.2 )的解,则对任意的uτ∈Hθ,t∈[τ,T],存在正常数K1及γ1,使如下估计成立:

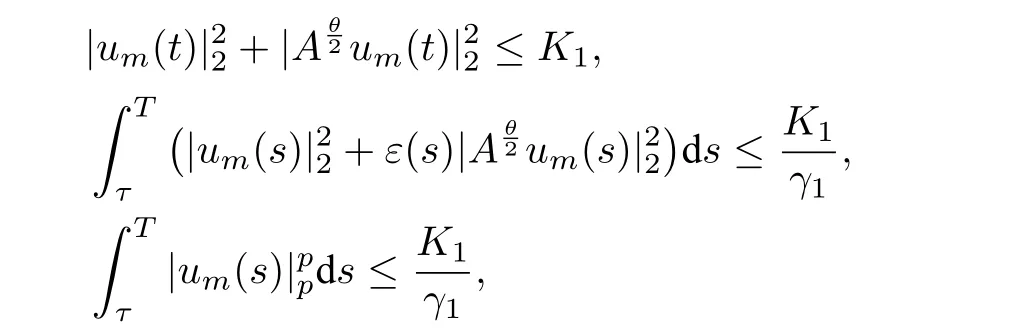
其中K1,γ1仅与初值和T有关.

证明用2um乘以系统(2.2)第一个方程两端并在Ω上积分,计算后得

由H¨older不等式和Young不等式,有

及

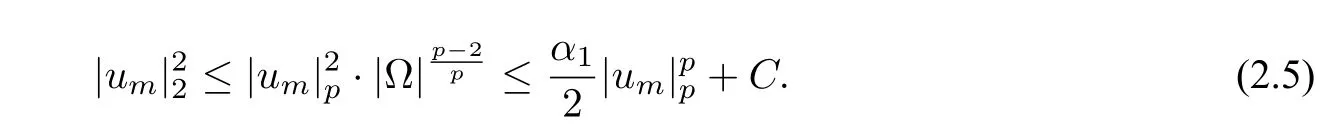
结合假设条件(H1)和(2.4 )–(2.5 ),(2.3 )可化为

利用(2.5),有

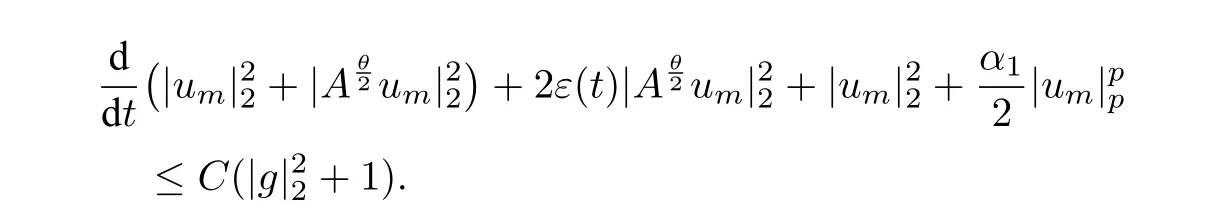
取γ1=min{1,},并对上式关于t从τ到t(t∈[τ,T])积分,得

引理2.2 若引理2 .1 的假设成立,则存在正常数K2,γ2,使得

成立,其中K2,γ2只与初值和T有关.

证明用2umt乘以系统(2.2)第一个方程的两端并在Ω上积分,计算后得

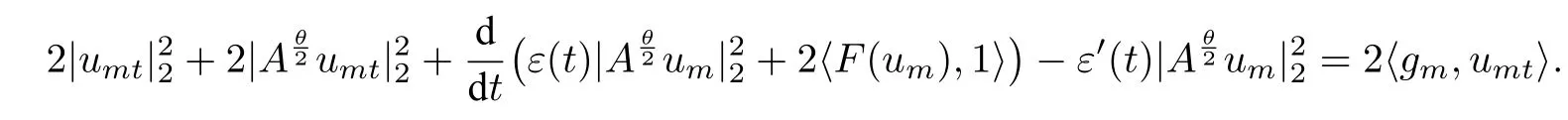
由Young不等式知

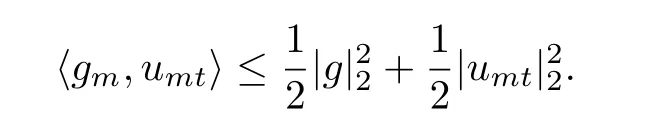
由引理2.1 及假设(H2),有

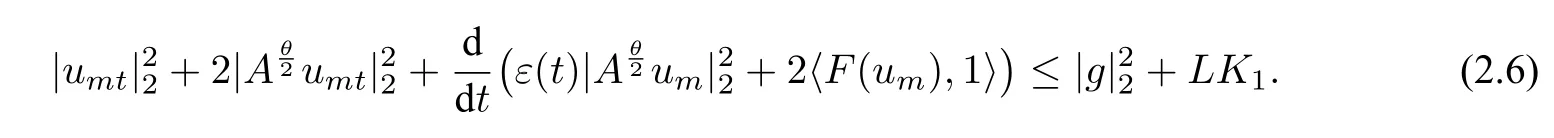
于是由(2.6)知

对上式关于t从s到t上积分并取τ≤s≤t≤T,结合假设(H1),得

对(2.7 )关于s从τ到T积分,然后不等式两边同除以T−τ,并结合引理2 .1 ,可得

结合假设(H1)和(2.8),有

取γ2=min{1,2α1},由上式可得,对任意的t∈[τ,T],有

对微分不等式(2.8)两边关于t从s到t积分(τ≤s≤t≤T),得

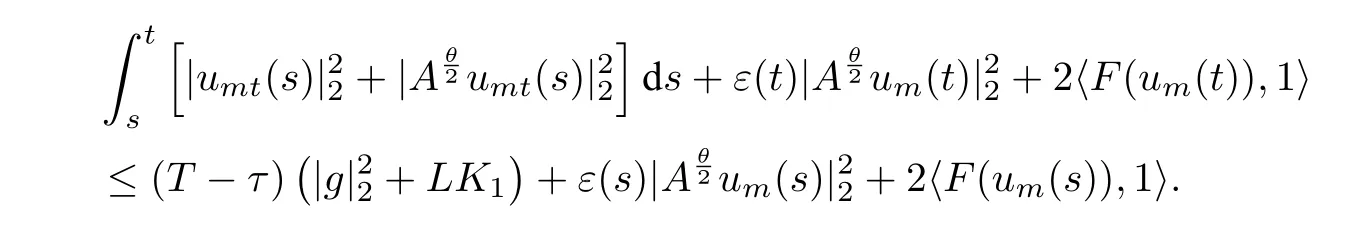
由假设条件(H1)−(H2)以及(2.8),可得

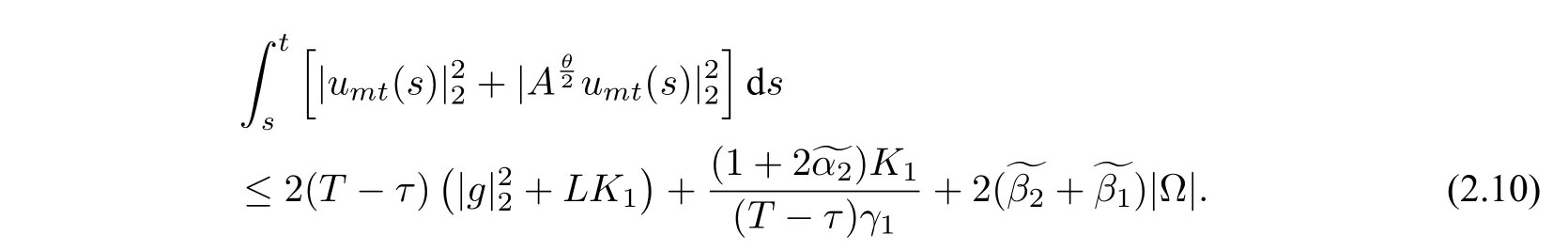
2.2 弱解的存在性

定理2.1 (弱解的存在性定理)设条件(H1)−(H2)成立,Ω⊂Rn(n≥3)是具有光滑或分段光滑边界的有界域,则对任意的T＞τ和uτ∈Hθ,系统(1.1 )–(1.2 )存在弱解u(t)满足

u∈C(τ,T;L2(Ω))∩L∞(τ,T;Hθ)∩Lp(τ,T;Lp(Ω));

ut∈L2([τ,T];Hθ).

证明由引理2 .1 和引理2 .2 可知,序列{um}满足:

um在L∞(τ,T;Hθ)中一致有界;

um在Lp(τ,T;Lp(Ω)中一致有界;

umt在L2(τ,T;Hθ)中一致有界.

由Alaoglu弱紧性定理以及所在空间的自反性知,存在{um}的子列(仍记为{um}),使得

um在L2(τ,T;Hθ)中弱收敛于u;

um在Lp(τ,T;Lp(Ω))中弱收敛于u;

umt在L2(τ,T;Hθ)中弱收敛于ut.

易知u∈L∞(τ,T;Hθ)∩Lp(τ,T;Lp(Ω))且ut∈L2(τ,T;Hθ).

因为q(p−1)=p,再结合引理2.1,有

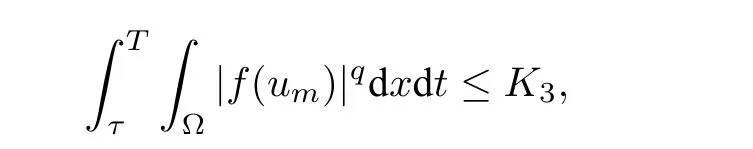
其中K3只与初值和T有关.所以

f(um)在Lq(Ω×[τ,T])中弱收敛于χ.

f(um(x,t))在[τ,t]×Ω中几乎处处收敛于f(u(x,t)).

由Lebesgue逐项积分定理可知,存在ϕ∈L2(τ,T;(Ω)),使得

故在Lq([τ,T]×Ω)中f(um)⇀f(u),同样在H−θ中有f(um)⇀f(u),由弱极限的唯一性知χ=f(u).

接下来我们验证u满足系统(2.1).为此取[τ,T]上的连续可微函数ψ使得ψ(T)=0.在方程(2.2)两端同乘以ψ(t)并对t积分,得

于是

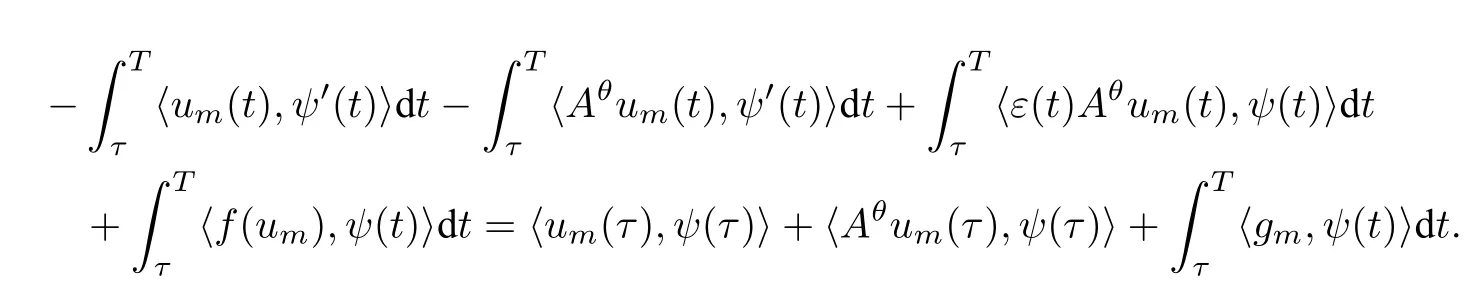
令m→∞,得

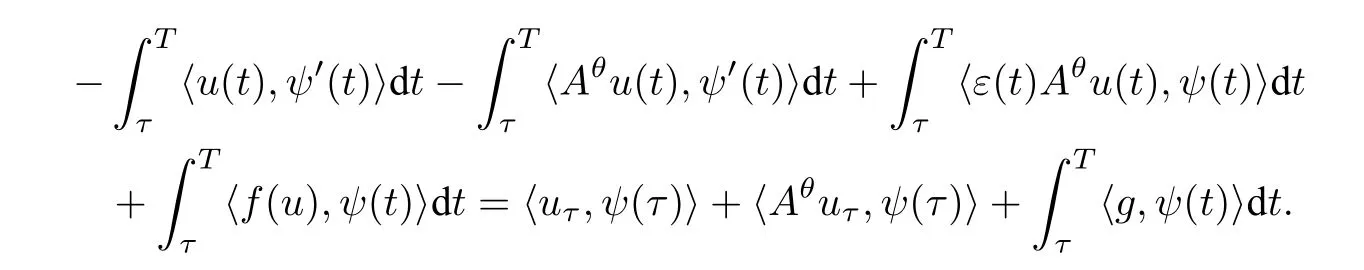
方程(1.1)可写为

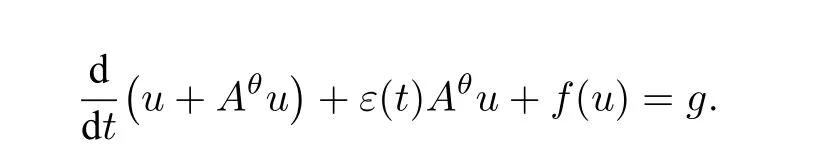
对任意的ψ(t)亦有

对上式关于变量t(t∈[τ,T])进行积分,得

于是

⟨uτ−u(τ),ψ(τ)⟩=0.

由ψ(τ)的任意性知u(τ)=uτ,定理证毕.

2.3 解的唯一性及其对初值的连续依赖性

定理2.2 设Ω⊂Rn(n≥3)是具有光滑或分段光滑边界的有界域,假设(H1)−(H2)成立.若方程(1.1 )存在满足初边值条件(1.2 )的弱解u(t),则该解是唯一的且是关于初值连续依赖的.

证明 假设ui(x,t)(i=1,2)为方程(1.1 )满足初边值条件(1.2 )在空间Hθ上的两个解,其对应的初值为uiτ(i=1,2).记ω=u1−u2,从方程(1.1)可得ω是如下初边值问题的解:

用2ω与方程(2.11 )的第一式在L2(Ω)上做内积,可得

由假设条件(H1)和(H2)可知

故

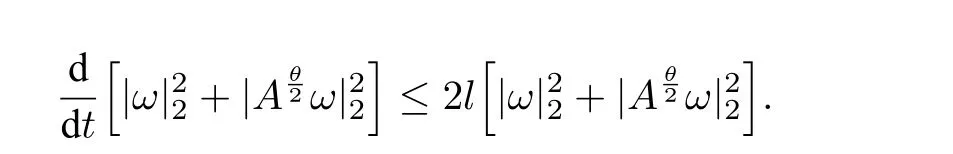
再由Gronwall引理可知