A Note on the Minimal Nonnegative Solution for Regular M matrix Algebraic Riccati Equations

Guan Jinrui Ren Fujiao

(Department of Mathematics,Taiyuan Normal University,Jinzhong030619,China)

Abstract Research on the theories and efficient numerical methods of M matrix algebraic Riccati equations(MARE)has become a hot topic in recent years.In this paper,we study the existence of minimal nonnegative solution for MARE and give a new proof to the existence of minimal nonnegative solution for the MARE associated with a regular M matrix,which is much simpler than the original proof.In addition,we give a wider condition to guarantee the existence of minimal nonnegative solution for the MARE,which is an extension of the existing results.

Key words Algebraic Riccati equation Regular M matrix Minimal nonnegative solution

1 Introduction

In this paper,we consider the M matrix algebraic Riccati equation of the form whereA,B,C,Dare real matrices of sizesm×m,m×n,n×m,n×n,respectively,and is an M matrix.

The M matrix algebraic Riccati equation arises from many branches of applied mathematics,such as transport theory,Wiener Hopf factorization of Markov chains,stochastic process,and so on[1,2,3,4,5].Research on the theories and the efficient numerical methods of nonsymmetric algebraic Riccati equation has become a hot topic in recent years[6,7,8,9,10,11,12].

The following are some notations and definitions we will use later.LetA=(aij)∈Rn×n.Ifaij≤0 for alli̸=j,thenAis called a Z matrix.A Z matrixAis called an M matrix if there exists a nonnegative matrixBsuch thatA=sI−Bwiths≥ρ(B)whereρ(B)is the spectral radius ofB.In particular,Ais called a nonsingular M matrix ifs＞ρ(B)and singular M matrix ifs=ρ(B).

Definition1.1([9])An M matrixAis said to be regular ifAv≥0for somev＞0.

The following lemmas can be found in[13].

Lemma1.1LetA∈Rn×nbe a Z matrix.Then the following statements are equivalent:

(1)Ais a nonsingular M matrix;

(2)A−1≥0;

(3)Av＞0for some vectorv＞0.

Lemma1.2LetA,Bbe two Z matrices.IfAis a nonsingular M matrix andA≤B,thenBis also a nonsingular M matrix.In particular,for any nonnegative real numberα,B=αI+Ais a nonsingular M matrix.

For equation(1.1),the solution of practical interest is the minimal nonnegative solution.Thus,the existence of minimal nonnegative solution is fundamentally important.In[3,6],under the condition thatKin(1.2)is a nonsingular M matrix or an irreducible singular M matrix,Guo proved the existence of minimal nonnegative solution for equation(1.1).

Theorem1.1([3,6])If K in(1.2 )is a nonsingular M matrix or an irreducible singular M matrix,then(1.1)has a minimal nonnegative solutionS.IfKis a nonsingular M matrix,thenA−SCandD−CSare also nonsingular M matrices.IfKis an irreducible M matrix,thenS＞0andA−SCandD−CSare also irreducible M matrices.

In[9],Guo extended the existence result to the case whenKin(1.2)is a regular M matrix.

Theorem1.2([9])If K in(1.2 )is a regular M matrix,then equation(1.1 )has a minimal nonnegative solutionSandD−CSis a regular M matrix.

Since nonsingular M matrices and irreducible singular M matrices are both regular M matrices,Theorem1.2 is an extension of Theorem1.1.However,the proof in[9]is too long and complicated.So,in this paper,we give a new proof of Theorem1.2,which is much short and simpler than the original proof.In addition,we extend the existence result to a general case.

2 Main Results

We will first give a new proof to Theorem1.2.

Proof SinceKin(1.2)is an M matrix,we knowDandAare M matrices.Chooseα＞0sufficiently large such thatαI−Dis a nonnegative matrix.In fact,if we chooseα＞max1≤i≤n{dii},thenαI−Dis nonnegative.Then,write equation(1.1)as the fixed point form

(αI+A)X=XCX+X(αI−D)+B,

and consider the iteration

(i)We first show by induction that the sequence{Xk}generated by(2.1)satisfies

0≤Xk≤Xk+1,k≥0.

Whenk=0,we have(αI+A)X1=B.Sinceα＞0andAis an M matrix,αI+Ais a nonsingular M matrix by Lemma1.2 and(αI+A)−1≥0by Lemma1.1.ThusX0≤X1=(αI+A)−1B.Suppose that0≤Xk≤Xk+1holds fork=l−1.Then we have

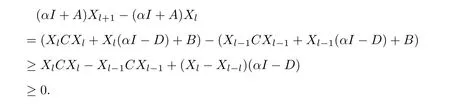
ThusXl+1≥Xl.By induction,0≤Xk≤Xk+1holds for allk≥0.

(ii)Next,we show that the sequence{Xk}is bounded above.SinceKin(1.2)is a regular M matrix,there is a vectorv=(v1,v2)T＞0such thatKv≥0.Thus we haveDv1≥Cv2andAv2≥Bv1.We now prove by induction thatXkv1≤v2for allk≥0.Whenk=0,it is evident thatX0v1=0≤v2.Suppose thatXkv1≤v2holds fork=l.We have

SinceαI+Ais a nonsingular M matrix,we have(αI+A)−1≥0by Lemma1.1.ThusXkv1≤v2holds fork=l+1.By induction,we knowXkv1≤v2holds for allk≥0.

Now,since the sequence{Xk}generated by(2.1)is monotonically increasing and bounded above,it has a limit limk→∞Xk=S.Take limit in(2.1 ),we know S is a nonnegative solution of equation(1.1 ).

In addition,since

(D−CS)v1=Dv1−CSv2≥Dv1−Cv2≥0,

D−CSis a regular M matrix.

In the following,we extend the existence result to some more general case.

Theorem2.1For the equation(1.1 ),if there exists a scalarδsuch that

is a regular M matrix,then(1.1)has a minimal nonnegative solutionSandD−CSis a regular M matrix.

ProofIt is evident that equation(1.1)has the same solutions with the equation SinceK′in(2.2 )is a regular M matrix,equation(2.3 )has a minimal nonnegative solutionSby Theorem 1.2.Thus equation(1.1)has a minimal nonnegative solutionS.

In the following,we give some illustrating examples of Theorem2.1.

Example2.1Consider equation(1.1 )with

It is easy to verify thatKin(1.2)is not a regular M matrix.However,for any0＜δ＜1,we can easily verify that

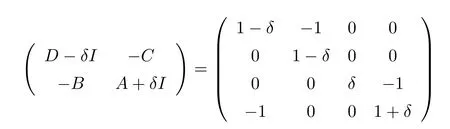
is a regular M matrix.Hence by Theorem2.1 ,equation(1.1 )has a minimal nonnegative solution.In fact,by direct computation,the minimal nonnegative solution is

Example2.2Consider equation(1.1 )with

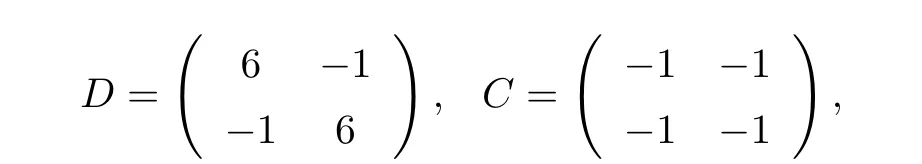
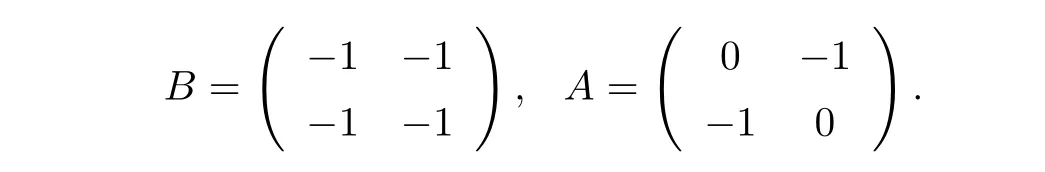
For this example,Kin(1.2)is not a regular M matrix.However,takeδ=3,we can see that

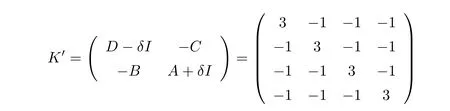
is an irreducible singular M matrix.Hence by Theorem2.1 ,equation(1.1 )has a minimal nonnegative solution.The minimal nonnegative solution is

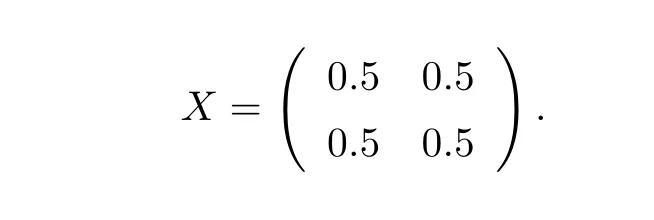
3 Conclusions

In this paper,we first gave a new proof to the existence of minimal nonnegative solution for MARE associated with a regular M matrix,which is much simpler than the original proof in[9].Then we gave a new result on the existence of minimal nonnegative solution,which is an extension to the existing results.In addition,some examples were given to illustrate the new results.