p2维融合范畴的扩张及应用
陈雅姝董井成
(1.南京信息工程大学数学与统计学院,南京,210044;2.南方科技大学数学系,深圳,518055)
1 引言
融合范畴是满足下列条件的刚性半单张量范畴:范畴只含有限个单对象;态射集是有限维的线性空间;单位对象1是单对象.融合范畴与数学和物理中的许多分支都有密切的联系,这些分支包括Hopf代数、量子群、顶点算子代数、拓扑量子场论、以及共形场论等[1–3].另外,融合范畴在量子计算中也有很突出的实际应用价值[4,5].由此可见,研究融合范畴不仅有助于完善融合范畴的自身理论体系,而且有助于数学和物理学的多个分支的发展和应用.融合范畴的扩张是构造融合范畴的有效方法之一,它在融合范畴的研究中有着重要的地位,融合范畴中的许多概念都建立在扩张结构之上,如融合范畴的幂零和可解的概念.但是,要研究融合范畴的任意扩张是一件很困难的事,因为这至少要包含有限群的分类.因此,目前看来一个可行的方案就是研究简单融合范畴在某一给定有限群下的扩张.在文献[6]中,本文第二作者已研究了Frobenius Perron维数是素数的融合范畴的扩张.在本文中,我们拟研究Frobenius Perron维数是素数平方的融合范畴的扩张.
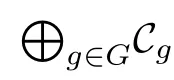
本文中所涉及的有关Hopf代数和融合范畴的基础理论和符号请参考[7]和[8].所有的Hopf代数和融合范畴都定义在一个特征为零的代数闭域上.
2 基础知识
2.1 Frobenius Perron维数
设C是一个融合范畴,K(C)是C的Grothendieck环,则C中单对象的同构类构成的集合Irr(C)是K(C)的Z+基.Frobenius Perron(FP)维数FPdim(X)定义为X在K(C)中的左乘得到的矩阵的最大特征值.由Frobenius Perron定理,FPdim(X)是一个正实数.此外,此维数可诱导出一个环同态FPdim:K(C)→R[9,定理8.6].C的FP维数定义为

如果单对象X的FP维数FPdim(X)=1,则称X是可逆的.如果一个融合范畴中的每个单对象都是可逆的,则称该融合范畴是顶点的.设Cpt是融合范畴C中全体可逆单对象生成的融合子范畴,则Cpt是C的最大的顶点融合子范畴.
如果FPdim(C)是整数,则称融合范畴C是弱整的;如果C中每个单对象的维数都是整数,则称融合范畴C是整的;如果C是弱整的,但C中至少有一个单对象的维数不是整数,则称融合范畴C是严格弱整的.
2.2 融合法则
设X∈Irr(C),Y是C中任意对象.X在Y中的重数定义为[X,Y]=dimHomC(X,Y),从而Y=⊕X∈Irr(C)[X,Y]X.设X,Y,Z∈Irr(C),那么[X,Y⊗Z]=[Y∗,Z⊗X∗]=[Y,X⊗Z∗],[X,Y]=[X∗,Y∗].
设G(C)是C中可逆单对象的同构类构成的集合,那么G(C)是一个群,其乘法是张量积.如果g∈G(C),X,Y∈Irr(C),那么
[g,X⊗Y]>0⇔[g,X⊗Y]=1⇔Y=X∗⊗g.
特别地,
[g,X⊗X∗]>0⇔[g,X⊗X∗]=1⇔g⊗X=X.
易知群G(C)在集合Irr(C)上有一个由左张量积诱导的左作用.因此,X⊗X∗的分解中可逆单对象是G(C)在集合Irr(C)上作用的稳定化子,记此稳定化子为G[X].于是,对于任意X∈Irr(C),有以下关系:
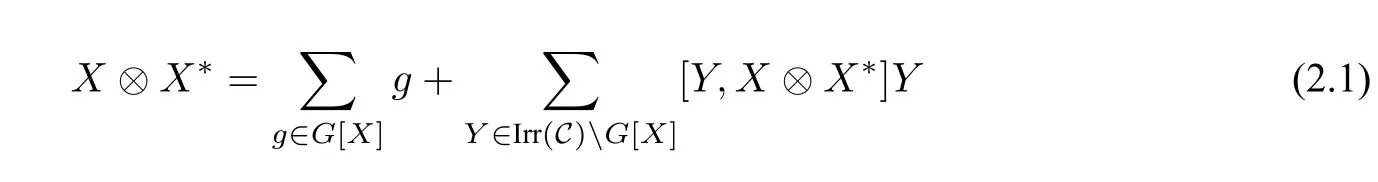
2.3 融合范畴的群扩张
设G是一个有限群.我们称融合范畴C具有一个G分次,如果C有一个满的abelian子范畴的直和分解C=⊕g∈GCg,使得(Cg)∗=Cg−1,且Cg⊗Ch⊂Cgh,∀g,h∈G,其中∗是对偶函子.如果对任意的g∈G,有Cg̸=0,则称C=⊕g∈GCg是一个忠实的G分次.在此情况下,C称为平凡分支Ce的G扩张.
由[10,命题8.20 ],如果C=⊕g∈GCg是一个忠实的G分次,那么对于任意的g,h∈G,有
FPdim(Cg)=FPdim(Ch),FPdim(C)=|G|FPdim(Ce).
通过直接验证,可得如下引理.
引理1设C=⊕
g∈GCg是平凡分支Ce的扩张,则C的包含Ce的子范畴与G的子群一一对应.
引理2设C=⊕
g∈GCg是平凡分支Ce的扩张,1=X1,X2,···,Xm是Ce所有非同构的单对象.如果分支Cg中存在一个1维单对象δ,则δ⊗X1,δ⊗X2,···,δ⊗Xm是Cg所有非同构的单对象.
证明易知δ⊗X1,δ⊗X2,···,δ⊗Xm∈Ce⊗Cg⊂Cg是Cg中互不同构的单对象.由FPdim(Ce)=FPdim(Cg)和FPdim(δ⊗X1)=FPdim(δ)FPdim(X1)=FPdim(X1)知δ⊗X1,δ⊗X2,···,δ⊗Xm是Cg中所有非同构的单对象.
每一个融合范畴C都有一个典范的忠实分次C=⊕g∈U(C)Cg,其平凡分支为Ce=Cad,其中Cad是C的由X⊗X∗中的单对象生成的伴随子范畴,其中X取遍Irr(C)中所有元素.此分次称为C的泛分次,U(C)称为C的泛分次群,见[10].
3 范畴型
3.1 一般分次群
设1=d0<d1<···<ds是一组正实数,n0,n1,···,ns是一组正整数.如果对任意的i,di维的非同构单对象的个数是ni,则称融合范畴C具有范畴型(d0,n0;d1,n1;···;ds,ns).
设融合范畴C=⊕g∈GCg是平凡分支Ce的扩张,其中dim(Ce)=p2,p是一个素数.如果Ce不是顶点融合范畴,则由[9,命题8.32]知Ce是一个Ising范畴.此时,C是一个交叉积融合范畴,见[11].在下文中,我们只考虑Ce是顶点融合范畴的情形.
引理3设融合范畴C=⊕g∈GCg是平凡分支Ce的扩张,其中dim(Ce)=p2,p是一个素数,则分支Cg中的单对象的个数和维数有以下三种可能的情况:
(1)Cg中有p2个1维的单对象;
(2)Cg中有p个维的单对象;
(3)Cg中有1个p维的单对象.
证明 由[9,命题8.32 ]知p2维融合范畴一定是顶点融合范畴,所以Ce中的单对象都是可逆的.因此Ce中的全体单对象关于张量积构成一个p2阶的群G(Ce).对于任意分支Cg中的任意一个单对象X,有X⊗X∗∈Cg⊗Cg−1⊂Cgg−1=Ce.因此,X⊗X∗是Ce中某些可逆单对象的直和.由(2.1 )知X⊗X∗中的所有可逆单对象构成G(Ce)的一个子群H.由于G(Ce)的阶是p2,H的阶只可能为1,p或p2.
如果|H|=1,那么dim(X⊗X∗)=dim(X)2=1,于是dim(X)=1.由引理2 知,Cg中的单对象都是1维的,所以Cg中有p2个1维单对象.
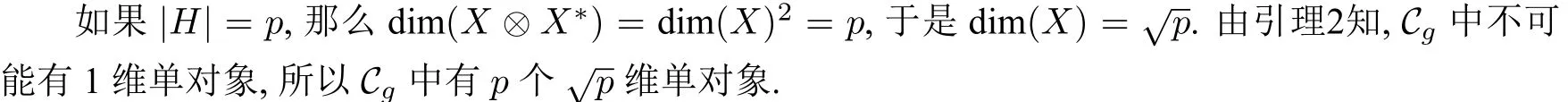
如果|H|=p2,那么dim(X⊗X∗)=dim(X)2=p2,于是dim(X)=p.由于dim(Cg)=p2,所以Cg中只含有1个p维单对象.
如果C中所有单对象都是1维的,那么C是顶点的融合范畴.文献[12]已给出顶点融合范畴的全部分类,因此在下文中我们总假设C不是顶点融合范畴.
引理4设融合范畴C=⊕g∈GCg是平凡分支Ce的扩张,其中dim(Ce)=p2,p是一个素数,则

由引理4(2)可得如下结论.如果G(Ce)=Zp2,则C具有范畴型(1,m;p,s)或(1,m;,n).
推论1设融合范畴C=⊕
g∈GCg是平凡分支Ce的扩张,其中dim(Ce)=p2,p是一个素数.
将引理3 ,引理4 总结如下:
定理1设融合范畴C=⊕
g∈GCg是平凡分支Ce的扩张,其中dim(Ce)=p2,p是一个素数,则C可能具有的范畴型为
(1)(1,|G|p2),其中|G|是群G的阶;
(2)(1,m;p,s);
(3)(1,m;,n),其中m=np;(4)(1,m;,n;p,s),其中m+sp2=np.
3.2 特殊分次群:G=Zq和S3
下面首先讨论当G为n阶循环群Zn={e,a,a2,···,an−1}时,融合范畴C=⊕
g∈GCg的范畴型.
引理5设融合范畴C=⊕g∈GCg是平凡分支Ce的扩张,其中dim(Ce)=p2,p是一个素数.如果分支Cg和Ch中的单对象都是1维的,则分支Cgh中的单对象也都是1维的.
证明设Irr(Cg)={δ1,δ2,···,δp2},Irr(Ch)={η1,η2,···,ηp2},其中dim(δi)=dim(ηi)=1,i=1,2,···,p2,则δ1⊗η1,δ1⊗η2,···,δ1⊗ηp2是分支Cgh中互不同构的p2个单对象,因此分支Cgh中的单对象也都是1维的.
引理6设融合范畴C=⊕g∈GCg是平凡分支Ce的扩张,其中dim(Ce)=p2,p是一个素数,G=Zn,且C具有范畴型(1,m;p,s).
(1)若存在Zn的某个生成元g0,使得分支Cg0中有p2个1维单对象,则C是顶点的融合范畴;(2)若存在Zn的某个生成元g0,使得分支Cg0中有1个p维单对象Xg0,则对于Zn的任意一个
生成元g,分支Cg都含有1个p维单对象.
证明(1)由于Zn=⟨g0⟩,故对任意的g∈Zn{e},存在某个正整数l,使得g=g0l.因此由引理5知分支Cg中的单对象都是1维的,从而C是顶点的融合范畴.

当循环群G=Zn的阶为素数时,我们有以下结论:
定理2设融合范畴C=⊕g∈GCg是平凡分支Ce的扩张,其中dim(Ce)=p2,G=Zq,p和q都是素数.
(1)若q=2,则C的范畴型可能为(1,2p2),(1,p2;,p)或(1,p2;p,1);
(2)若q为奇素数,则C的范畴型只可能为(1,qp2)或(1,p2;p,q−1).

dim(C)=|Zq|dim(Ce)=qp2=|Z2|dim(C1)=2np,

如果C中只有1维单对象,那么C具有范畴型(1,qp2).
如果C中只有1维单对象和p维单对象,那么由引理6 知任意的非平凡分支Cg中都有一个p维单对象,因此C具有范畴型(1,p2;p,q−1).

综上所述,当q为奇素数时,C的范畴型只可能为(1,qp2)或(1,p2;p,q−1).
其次,我们探讨当G为对称群S3时,融合范畴C=⊕
g∈GCg的范畴型.
对称群S3可以抽象地表示为S3=⟨a,b|a3=e,b2=e,(ab)2=e⟩={e,a,a2,b,ab,a2b}.由于3阶循环群Z3={e,a,a2}是S3的一个子群,故由引理1 知,Ce⊕Ca⊕Ca2是一个融合子范畴,进一步由引理6 和定理2 可得:
引理7设融合范畴C=⊕g∈GCg是平凡分支Ce的扩张,其中dim(Ce)=p2,p是素数,G=S3,则分支Ca和Ca2中只可能有整数维的单对象,并且
(1)分支Ca中有p2个1维的单对象当且仅当分支Ca2中有p2个1维的单对象;
(2)分支Ca中只有1个p维的单对象当且仅当分支Ca2中只有1个p维的单对象.

引理9设融合范畴C=⊕g∈GCg是平凡分支Ce的扩张,其中dim(Ce)=p2,p是素数,G=S3.如果分支Cb中的单对象都是1维的,那么
(1)当分支Ca和Ca2中只有1维单对象时,C是顶点的融合范畴;
(2)当分支Ca和Ca2中分别有一个p维单对象Xa和Xa2时,C具有范畴型(1,2p2;p,4).
证明(1)由引理5 知,分支Cab和Ca2b中的单对象都是1维的,因此C是顶点的融合范畴.
(2)设δb是Cb中的一个1维单对象,则Xa⊗δb和Xa2⊗δb分别是Cab和Ca2b中的p维单对象,因此C具有范畴型(1,2p2;p,4).
引理10设融合范畴C=⊕g∈GCg是平凡分支Ce的扩张,其中dim(Ce)=p2,p是素数,G=S3.如果分支Cb中只有1个p维的单对象Xb,那么
(1)当分支Ca和Ca2中只有1维单对象时,C具有范畴型(1,3p2;p,3);
(2)当分支Ca和Ca2中分别有一个p维单对象Xa和Xa2时,C可能具有的范畴型为(1,2p2;p,4)
或(1,p2;p,5).
证明(1)设δa和δa2分别是Ca和Ca2中的1维单对象,则δa⊗Xb和δa2⊗Xb分别是Cab和Ca2b中的p维单对象.因此,C具有范畴型(1,3p2;p,3).
(2)由引理8 知,分支Cab和Ca2b中不可能有维的单对象,于是分支Cab和Ca2b中只可能含有p2个1维单对象或者1个p维单对象.注意到分支Cab和Ca2b中不可能同时只含1维单对象,否则由引理5 ,分支Ca2b·ab=Ca中只含1维单对象,矛盾.因此C可能具有的范畴型为(1,2p2;p,4)或(1,p2;p,5).

综合以上讨论,我们得如下定理.

4 半单Hopf代数
有限维Hopf代数的一个正合序列是一个Hopf代数映射的序列
k→Ki−→Hπ−→L→k,
它满足:
1.i是单射,π是满射;
2.π◦i=εK1,其中εK是K的余单位;
3.kerπ=HK+.
如果K是交换的,L是余交换的,那么该正合序列称为abelian扩张.在此情况下,存在有限群Σ和Γ,使得K∼=kΣ,L∼=kΓ,并且有

如果一个Hopf代数H符合正合序列(4.2),那么,作为Hopf代数,H关于某个正规化的2 余循环τ和σ,同构于双交叉积kΣτ#σkΓ.关于Hopf代数的abelian扩张理论的详细研究请参考[14].
如果kΣ在H的中心里,则称正合序列(4.2 )为中心的.如果其对偶是中心的,称正合序列(4.2 )是余中心的.由[15,引理3.3 ],如果正合序列(4.2 )是中心的,那么σ是平凡的;如果正合序列(4.2 )是余中心的,那么τ是平凡的.
定理4设H是半单的Hopf代数.如果H的表示范畴Rep(H)=⊕g∈GCg是平凡分支Ce的扩张,其中dim(Ce)=p2,p是素数,则H=kGτ#σkΓ是一个双交叉积,其中Rep(kΓ)=Ce且σ是平凡的.
证明由[10,定理3.8],我们有Hopf代数的中心正合序列

其中i是嵌入映射,π是自然投射,K=H/H(kG)+且Rep(K)=Ce.由p2维半单Hopf代数的分类知K是群代数,从而存在一个p2阶的群Γ使得K=kΓ.因此,上述正合序列是一个abelian扩张.这样,H=kGτ#σkΓ是一个双交叉积且σ是平凡的.

