射影平面上点的合冲
莫佳丽 余琪
(苏州大学数学科学学院,苏州,215006)
1 引言
合冲这一词在18世纪被用于天文学,用来描述3个行星位于一条直线上的现象.Hilbert在模的自由分解中借用了这个概念.他在[1,2]中证明了著名的“Hilbert合冲定理”:对有r+1个生成元的坐标环S,任何有限生成分次S模M都有一个有限的自由分解:Fr+1−→···−→Fn−→Fn−1−→···−→F1−→F0,其中n≤r+1.
Hilbert合冲定理在代数几何领域有着广泛的应用.从代数几何的角度出发,我们通过坐标环S=K[x0,x1,···,xr]来研究合冲.假设M是一个S模,M⊂M是M生成元的集合,F=SM,f:F−→M是把F的基元素映射为M的生成元的一个映射,若M是分次的,则可以通过选择其齐次生成元来保持分次.我们用M1表示M的第一个合冲模,Mk来表示M的第k个合冲模.根据文献[12],M1就是映射f的核,因此M1也是分次S模.按照同样的方法,我们可以通过递归给出M的其他次数的合冲模.
在代数几何领域,利用合冲,可以得到正则度,Betti数,Hilbert函数等信息.Green[3]和Lazarsfeld[4]从代数几何的角度研究了射影代数曲线的合冲.之后,Maroscia[5]和Nagel[6]将其结果推广到高维射影空间.在[7–10]中提到了代数簇合冲理论的最新进展.关于代数簇合冲的综述我们可以参考Lazarsfeld的名著[11]的第一章.从Hilbert开始,齐次理想的合冲及其对应的代数集,一直是许多数学家感兴趣的问题.我们知道点是最简单的代数集,Eisenbud等人给出了平面上点的合冲的一些性质,并对平面上3个点,4个点以及5个点的情形做了细致的研究.文献[12]和[13]系统讨论了点的合冲问题,并给出了一些几何上的应用.但是点(包括其对应的0维概形)的合冲问题还没有被完全解决.
代数几何中的一个基本问题就是对代数曲线对应的线性系进行分类.这起源于小平邦彦关于椭圆纤维化的工作[14−16].本文的目标就是通过研究射影平面上点的合冲,用新的观点对平面椭圆曲线对应的线性系进行分类.
众所周知,平面椭圆曲线一定是光滑的平面三次曲线.因此,对平面椭圆曲线族进行分类,只需对平面三次曲线对应的线性系进行分类.因为平面三次曲线对应的线性系一定有基点(所有一般元的公共交点),本文从合冲的角度来考虑这些基点对应的平面三次曲线线性系,进而对平面三次线性系进行分类.我们首先给出平面上7个不同点的所有合冲的表达及其对应的饱和齐次理想的极小自由分解,并在前人结果([12],[17])的基础上,证明一共有11种不同的平面三次线性系.
2 预备知识
本文所有的研究对象都是在特征0的代数闭域K上.下面给出我们要用到的一些结论.
下面的命题1是由Hilbert合冲定理得到的.
命题1([12])若IX⊆K[x0,x1,x2]是平面上有限个点的齐次理想,则IX有一个长度为1的极小自由分解.
每个长度为1的自由分解都满足下面的定理1,这是我们求解平面上点的合冲的关键.

由定理1 可知,计算点的合冲的关键是确定其理想对应的生成元.因此生成元的数目和次数是我们需要重点考虑的.首先,我们可通过下面的引理1 确定生成元的数目.
引理1([18])若X位于一个次数为d的曲线上,则IX至多有d+1个生成元.此外,生成元的次数也可以由其对应理想的正则度确定.
定义1设X={p1,···,pn},且对于每个ϕ:X→K,都存在f∈K[x1,···,xn],degf≤d,满足f=ϕ|X,则称满足这个关系的最小的整数d为X的插值次数(interpolation degree).
若存在F1,···,Fn∈Sd,当且仅当j=i时使得Fj(pi)不为0,则X在次数为d的多项式形式上是独立的.
定理2([12])设M是一个有限生成分次S模,X⊂Pr是一个非空点集,且M=SX,则M的正则度等于X的插值次数.
根据定理2,我们可以得到一个重要推论.

为了方便读者阅读,我们给出几个常用的平面代数曲线定理,它们的证明可以参考[19].
定理3(贝祖定理)对于无公共分支的代数曲线C1,C2⊂P2(K),有

定理4(诺特“AF+BG”定理)设F,G,H是射影平面曲线.若F,G没有公共分支,则当且仅当在每一点p∈F∩G上都满足诺特条件时,有H=AF+BG成立,其中A,B的次数分别为deg(H)−deg(F),deg(H)−deg(G).
诺特条件见参考文献[19].
定理5(沙勒定理)设F,G是两条平面三次曲线,交9个不同的点,如果另一条三次曲线过其中8个点,则它也一定过第9个点.
3 主要结果
我们需要射影平面(以下简称平面)上6,7个点的合冲关系.Henke[17]给出了射影空间中6个点的合冲的结果和证明,作为其结果的一个推论,我们得到平面上6个点的合冲的具体形式:

现在我们对平面上7个不同的点合冲进行分类.以下的定理6 是本文的主要定理.
定理6设X⊂P2是平面上7个不同的点,IX是X的饱和的齐次理想,则根据7个点的不同位置可得IX在各种情形下的极小自由分解:

注1(1)在下面的证明中,生成元是在饱和齐次理想中考虑的,所有的曲线用大写字母表示,多项式用小写字母表示,且各种情形中的字母都互不相关.
(2)我们计算所得的合冲,已经用CoCoA软件进行了逐一验证.
证明情形(1)X中7个点在一条直线上.由引理1 可知,IX至多有2个生成元,且其中一个生成元的次数为1,即a2=e1=1,根据定理1 进行简单的计算即可得定理的结果(1).
情形(2)X中有6个点在一条直线L上.显然X位于一条二次曲线上,因此由引理1 知,IX至多有3个生成元.若有2个生成元,则X是完全交,由贝祖定理知这种情况不会发生,故必有3个生成元且存在一个二次生成元.因剩下一点只能确定一个2维的一次线性系,所以IX一定有两个次数为二的极小生成元,因此a3=e1+e2=2,a2=e1+f2=2,由定理1 即可得结果(2).
情形(3)X中有5个点在一条直线L上.与结果(2)同理,IX必有3个生成元且存在一个二次生成元.若还有一个二次生成元,由贝祖定理可知此二次曲线过这7个点时必以L为分支,且剩下两点确定唯一一条直线,因此二次生成元唯一.除直线L外的两点可构造一个不可约的二次曲线过这两个点,故X可位于三次曲线上,因此三次生成元存在且a3=e1+e2=2,a2=e1+f2=3.由定理1 有e1,e2,f2≥1,故e1=e2=1,f2=2,且7=e1f1+e1f2+e2f2=f1+2+2.因此f1=3,a1=f1+f2=5,b1=a1+e1=6,b2=a2+e2=4.由此易得极小自由分解(3).
情形(4)X中有4个点在一条直线L1上,另外3个点共线于L2.同情形(2)可得必有3个生成元且存在一个二次生成元;同情形(3)可得二次生成元唯一.若有三次生成元g3,由贝祖定理可知g3对应的三次曲线以L1为分支.令L1对应的多项式为l1,则g3=l1h2,其中h2是二次多项式,其对应曲线记为H2.再次使用贝祖定理,得H2以L2为分支,故三次曲线可由二次曲线生成,即不存在三次生成元.我们以L1为分支的曲线,然后再取互不相同的3条直线分别过剩下共线的3个点即可构造出四次生成元所对应的四次曲线,这时四次生成元存在,且全部生成元的次数为2,4,4.此时得到结果(4)的过程同情形(3)类似.


图1 三次曲线过7个点

图2 四次曲线过7个点
情形(6)X中有7个点位于一个不可约二次曲线上.此时与情形(2)同理,可得IX必有3个生成元且存在一个二次生成元,此二次生成元不可约,由贝祖定理可知仅有一个二次生成元;若有一个三次生成元,由贝祖定理知,此三次生成元对应的三次曲线以二次不可约曲线为分支,矛盾.由于X中7个点对三次曲线是独立的,根据推论1,IX生成元次数≤4.由上述分析可知IX必有四次生成元,因此3个生成元次数分别为2,4,4.最后根据定理1 可得极小自由分解(6).
情形(7)X中3个点在一条直线上,另4个点中有3个点不在一条直线上.
情形(8)X中3个点在一条直线上,另4个点中有3个点在一条直线上.
情形(9)X中有6个点位于一个不可约二次曲线上.
情形(10)X中没有6个点位于一个不可约二次曲线上且没有3个点在一条直线上.
这4种情形的证明方法类似,下面给出具体的证明步骤.
第一步:先证明只有3个三次生成元.
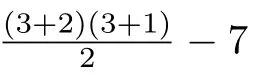
第二步:证明四次生成元不存在.
假设这3个三次生成元分别为g3,,,且由贝祖定理知这3个三次生成元对应的三次曲线中有两个三次曲线无公共分支,为了方便计算假设这两个三次曲线对应的多项式分别为g3,若还有一个四次生成元,则把其对应的四次曲线的多项式记为g4.由于7个点对四次曲线是独立的,故四次曲线过7个点独立参数维数为:=8.由g3,,所生成的四次曲线为:l1g3+l2+l3,其中li(i=1,2,3)是一次多项式且每个li的独立参数维数为3,若l1g3与l2g参数相关,则有l1g3=−l2g′3,可推出l1|l2或l1|.若l1|l2,在不考虑相差一个常数倍的情况下,令l1=l2,那么g3=−,矛盾;若l1|,则有g3=−l2h2,其中=l1h2,h2是二次多项式,与g3,对应的2个三次曲线无公共分支,矛盾.因此l1g3与l2参数不相关,故g3,生成的四次曲线的独立参数维数为6.
故IX只有3个生成元,且生成元次数都是三.那么a3=e1+e2=3,a2=e1+f2=3,a1=f1+f2=3,由定理1,e1,e2,f2≥1,fi≥ei,fi≥ei+1,(i=1,2),我们可以推出e1=f1=2,e2=f2=1,且满足7=e1f1+e1f2+e2f2,则b1=a1+e1=3+2=5,b2=a2+e2=3+1=4.则极小自由分解显然得证.
4 射影平面上三次线性系的分类
设X⊂P2是射影平面上的一个有限点集,IX是X对应的饱和齐次理想.我们考虑是否存在平面曲线族Cλ恰好以X中所有点为基点.以下,我们对平面三次曲线对应的线性系用合冲的观点来讨论这个问题.
首先,我们有下面的命题.
命题2 三次线性系{λ1s1+···+λksk}的基点数目≤9,其中si是三次曲线,λi∈P1.
证明令D={λ1s1+···+λksk},任取A1,A2∈D.由于A1,A2这两个一般元是不可约三次曲线且无公共分支,由贝祖定理知A1与A2交点数为9.令这9个交点分别为p1,···,p9,由定义知p1,···,p9为D的基点.若再取A3∈D,则A1,A2与A3交点数≤9,结论得证.
下面对基点数目是8和9两种情况进行分类.
定理7若三次线性系D的基点数目为9,则该三次线性系一定有2个生成元即D=
{λ1s1+···+λksk}=<s1,···,sk>=<B1,B2>.
证明∀B1,B2∈D,B1,B2是一般元,且这两个一般元是不可约三次曲线且无公共分支,则<B1,B2>⊆<s1,···,sk>是显然的.下面证明<s1,···,sk>⊆<B1,B2>,即证所有si∈<B1,B2>.因为B1,B2的交点数目为9,即B1,B2都过这9个点.又因si过这9个点,由诺特“AF+BG”定理,∃a,b∈K,使si=aB1+bB2,从而si∈<B1,B2>.结论得证.
沙勒定理[17]告诉我们两条平面三次曲线交9个不同的点,如果另一条三次曲线过其中8个点,则一定过第9个点.因此我们有下列推论:
推论2当基点数目为8时没有对应的三次线性系.
我们从合冲的角度来对平面三次线性系{λ1s1+···+λksk}进行分类,I=<s1,···,sk>,基点集A=V(I)=V(s1,···,sk).由[12],[17]和定理1 关于点的合冲的分类,可以得出11个不同的三次线性系.

(4.3)给出的是11个不同的三次线性系对应的合冲,其中,的(1)与(2)是基点数目为1与2的时候对应的合冲;(3)与(4)是基点数目为3的时候对应的合冲,分别对应于3点位于一条直线上和3点不位于一条直线上.(5)与(6)是基点数目为4的时候对应的合冲,分别对应于3个点位于一条直线上和4个点位于不可约的二次曲线上.(7)是基点数目为5的时候对应的合冲,对应的情况为3个点位于一条直线上和5个点位于一条不可约的二次曲线上这两种.(8)与(9)是基点数目为6的时候对应的合冲,分别对应于6个点位于一条特殊的二次曲线上且没有大于3个点在一条直线上和6个点不位于二次曲线上且没有3个点在一条直线上.(10)是基点数目为7的时候对应的合冲,对应某3个点位于一条直线上,另4点在一条直线上;某3个点位于一条直线上,另4点不在一条直线上;6个点在一条不可约的二次曲线上;没有6个点位于不可约二次曲线上且没有3个点在一条直线上这四种情形.(11)是基点数目为9的时候对应的合冲,此种情况为完全交.
以上11个合冲对应11种不同的三次线性系,现在我们来对这些线性系进行分类,由于表述类似,以下选择基点数目为2,4和9的情形来进行说明:
1.当基点数目为2时,三次曲线对应的线性系Ch2,l1:=h2g1+l1g2=0,其中l1=a1x+b1y+c1z,h2=a2x2+b2y2+c2z2+d2xy+e2xz+f2yz,且a1,b1,c1,a2,b2,c2,d2,e2,f2是定义在K上的参数;g1,g2是对应的极小自由分解的一次生成元和二次生成元.
2.当基点数目为4时,有两种情形:
(1)有3个基点位于一条直线上.此时三次曲线对应的线性系Cl1,l2,k:=l1g2+l2g+kg3=0,这里li=aix+biy+ciz(i=1,2),且ai,bi,ci,k是定义在K上的参数;g2,g3是对应的极小自由分解的2个二次生成元和1个三次生成元.
(2)4个基点位于不可约的二次曲线上.此时三次曲线对应的线性系Cl1,l2:=l1g2+l2=0,这里li=aix+biy+ciz(i=1,2),且ai,bi,ci是定义在K上的参数;g2,是对应的极小自由分解的2个二次生成元.
3.当基点数目为9时,只有一种完全交情况,即生成元只有2个,且次数都为三.此时三次曲线对应的线性系Cλ,µ:=λg3+µ=0,这里λ,µ是两个定义在K上的参数,g3,是对应的极小自由分解中的三次生成元.
- 数学理论与应用的其它文章
- Peakon,Pseudo Peakon,Periodic Peakon and Compacton Determined by Exact Solutions of Singular Nonlinear Traveling Wave Systems
- On the Geodesic transitivity of Finite Graphs
- Extended Binding Number Results on Fractional(g,f,n,m) critical Deleted Graphs
- Higher Accuracy Shape-preserving Modeling Based on the Two-level Fitting Method
- A Note on the Minimal Nonnegative Solution for Regular M matrix Algebraic Riccati Equations
- p2维融合范畴的扩张及应用

