考虑冻胀力和冻结力作用的梯形渠道衬砌冻胀破坏弹性地基梁模型

何鹏飞，马巍，穆彦虎，董建华，黄永庭

(1. 兰州理工大学理学院，甘肃兰州，730050；2. 中国科学院西北生态环境资源研究院冻土工程国家重点实验室，甘肃兰州，730000；3. 兰州理工大学土木工程学院，甘肃兰州，730050；4. 中国科学院大学，北京，100049)

全年地表温度持续低于0 ℃或最冷季节气温低于0 ℃的地区称为冻土区，地球上陆地面积约50%区域属于冻土区[1]。在土体冻结过程中，孔隙水冻结后体积会增大9%引起冻胀，同时，在温度梯度作用下未冻土内水分通过毛细作用向冻结缘迁移，形成分凝冰，也会引起冻胀[2]。因此，冻土地区的工程建筑经常遭受冻胀作用的危害。

在中国，约有52%陆地属于冻土区，其中在中国西北部的新疆维吾尔自治区，地处中温带干旱区，冬季寒冷干旱，分布有大面积的季节性冻土[3]。该地区日最高气温低于0 ℃的持续时间可达130 d，并且昼夜温差较大。由于降水稀少并且水资源分布极其不均匀，为满足城市生产生活及农田灌溉需求，这些地区修建了大量水库和长距离引水渠道，西北地区农田超过90%灌溉用水依赖引水渠道供给[4−5]。为降低渗漏，输水渠道通常在渠坡和渠底铺设混凝土衬砌，以提高渠系水利用效率[6−7]。但在多年运行过程中，由于反复的冻融及水力冲刷等外部荷载作用，不可避免地造成衬砌和接缝破裂引起渗漏。在输水期渗漏可使基土流失、渠坡垮塌及衬砌架空失稳。在冬季停水期，由于降雨、渗漏及地下水的迁移，在渠道停水后渠基土含水率往往较高。如果土体冻结前水分没有排干，那么，冻结期将会有充分的水分产生冻胀。此外，季节冻土区温度下降缓慢，冻结速率相对较小，水分有充足的时间迁移至衬砌附近土体，从而引起显著的冻胀作用[8]，有些地区渠道基土的冻胀变形可达15 cm[3]。由于坡板衬砌与底板衬砌和上部马道相互约束，冻胀变形无法释放，引起的冻胀力在极端情况下会使衬砌断裂，进一步加剧输水期渠道渗漏，导致输水渠道处于“冻胀—衬砌破坏—渗漏—更严重冻胀”的恶性循环中。如肖旻[9]调查发现新疆塔里木灌区输水渠道衬砌存在严重的冻胀问题，尤其是刚性衬砌渠道。QIN等[4]发现新疆地区水库的混凝土面板在冻胀力和冰压力作用下，在冬季水位线附近易出现裂缝。孙江岷等[10]的调查表明黑龙江地区水库和输水渠道也存在严重的衬砌面板冻害问题。TIAN 等[11]研究表明青藏铁路路基排水沟渠的混凝土衬砌在横向发生破坏的主要原因是水平冻胀力，在纵向发生破坏的主要原因是不均匀冻胀位移。在其他的高寒区水利工程中也存在由于冻胀作用导致的衬砌破坏问题[12−14]。此外，在春季土体逐渐融化的过程中，由于孔隙冰和分凝冰融化使基土含水率升高，导致基土强度和承载力下降，引起过大的变形甚至渠坡的滑塌[15]。

为提高寒区输水渠道的使用效率，推进渠道抗冻胀设计方法和防冻胀措施的深入研究，人们对冻土地区混凝土衬砌冻胀破坏机理进行了大量的理论计算和试验研究，为存在严重冻害的渠道修复和病害处置提供参考。LI等[16−17]对衬砌渠道的冻胀破坏机理进行了数值模拟，较全面地反映了渠道冻结过程中温度场、水分场和变形场的变化过程。但模拟过程中考虑的影响因素较多，计算过程复杂、繁琐，限制了其在工程实践中的应用。因此，通过简单、方便的理论计算方法分析冻胀作用下衬砌的受力特征和破坏机理仍然十分必要。王正中[18]对高寒区输水渠道衬砌的破坏形式进行了调查，发现不均匀冻胀变形是引起衬砌断裂的主要原因。他通过构建力学模型，将衬砌板简化为简支梁结构，使用材料力学方法对冻胀力和冻结力同时作用下的不同断面形状的混凝土衬砌进行了受力分析。计算结果与现场试验基本吻合，但模型中对冻胀力和冻结力的简化较多。此后，人们使用这一模型对不同条件下衬砌在冻胀作用下的受力和变形特征进行了分析，对破坏位置和引起破坏的条件进行了预测[19−21]。

由于寒区渠道衬砌特殊的板壳结构形式，在冬季经受冻胀变形及春季融沉后具有一定的复位能力。在渠系工程抗冻胀设计规范中规定：寒区渠道衬砌允许产生一定的冻胀位移，以达到消减冻胀、降低成本的目的，并以不产生残余位移和累积冻胀变形为依据给出了冻胀位移允许值。规范中推荐了不同的地区、土质、地下水位和渠道走向时基土的冻胀变形计算方法，但没有说明衬砌变形的计算方法。衬砌的变形过程和基土的冻胀过程总是同步进行和相互作用的，以往的力学模型根据材料力学理论建立，无法反映衬砌与冻土的相互作用关系。为克服这一缺陷，肖旻等[22−23]基于Winkler弹性地基梁理论，构建了以衬砌冻胀位移计算为基础的衬砌冻胀内力计算方法和冻胀破坏判断准则，计算结果与现场监测数据基本吻合。但在肖旻等[22−23]建立的模型中，忽略了衬砌与冻土界面切向冻结力对衬砌变形和内力的影响，衬砌作为一种薄板结构，切向冻结力的作用易使其发生偏心弯压，其作用不可忽略。

为此，本文作者以高寒地区输水渠道衬砌在非均匀冻胀作用下的变形为研究对象，基于弹性地基梁模型建立考虑非均匀法向冻胀力和切向冻结力作用下的力学模型，得到现浇梯形渠道衬砌底板和坡板挠度微分方程的解析解，结合典型工程案例对衬砌的变形和受力特性，以及切向冻结力的影响进行分析。

1 衬砌力学模型的建立和求解

1.1 基本假设和约定

冻土的冻胀过程和衬砌的变形过程是相互作用的。冻土的冻胀作用产生的冻胀力会引起衬砌变形，而衬砌的变形释放了冻胀力，削弱了冻胀力对衬砌的作用力。在渠道的冻结过程中，冻胀力和冻胀变形最终达到平衡，此时衬砌的变形曲线为渠道衬砌冻胀变形的实际曲线，由此可以得到渠道衬砌冻胀位移的分布规律。在渠道基土发生冻结的过程中，由于冻胀变形的作用，坡板衬砌与基土之间出现相对滑动，使界面产生冻结力(剪切力)，这个冻结力的最大值通常称为冻结强度。

以工程中常见的开放系统梯形混凝土衬砌渠道为例，基于弹性地基梁理论，将衬砌板简化为梁，如图1 所示。图1 中，A点和B点分别为坡板衬砌的底端和顶端，梁厚度为h，宽为b，长度为l，梁与地基间的相互作用通过一系列的弹簧构件实现，梁上各点的冻胀力仅由各点对应的冻胀变形(弹簧变形)决定。

图1 衬砌板弹性地基梁计算模型Fig.1 Elastic foundation beam model of canal lining

结合已有的研究成果和工程实践经验，补充以下假设和约定[18,22−24]：

1)衬砌纵向长度远比横向长度大，渠道衬砌力学模型简化为二维平面应变问题。

2)由于冬季冻结过程缓慢，将衬砌变形过程视为准静态过程。冻胀发生过程中冻土与衬砌的变形总是相互协调的，结构破坏时衬砌处于极限平衡状态。

3)渠道衬砌变形处于线弹性范围内，仅考虑衬砌的小变形，忽略微元体的转动作用。

4) 冻胀计算仅考虑冻深范围内冻土的变形，不考虑冻结深度以外冻土的固结变形。

5)渠道建成后衬砌自重与基础反作用力相互平衡，受力分析时不考虑衬砌自重的影响。

1.2 模型的建立和求解

取衬砌板上某一微段进行受力分析(图2)。

图2 衬砌微段受力分析Fig.2 Force analysis of lining freebody

对微元体右侧中点取矩，由∑M= 0，有

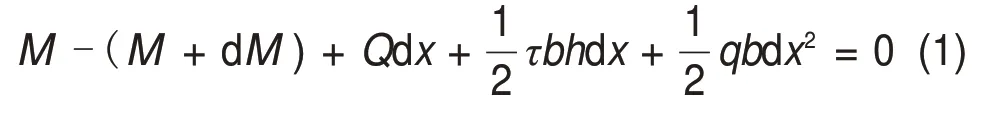
式中：M，Q和P分别为截面弯矩、剪力和轴力；dM，dQ和dP分别为截面弯矩、剪力和轴力的微量；q为地基反力(冻胀力)；τ为摩阻力(切向冻结力)；dx为微段的长度。

忽略式(1)中高阶微分项，可得

对微元体y方向取力平衡方程，由∑Fy= 0，可得

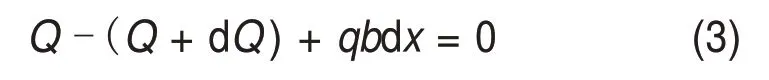
化简可得

对于特定的地区，其土质、气候等因素相似，地下水的补给强度是决定断面各点冻胀强度(冻胀率)的主要因素[22]。研究表明[22,25−26]，冻土的冻胀强度与地下水埋深关系可表示为

式中：η0为冻胀率，%；z为与地下水位距离；a1和b1为与气象和地质条件有关的经验参数。

由式(6)可以计算得到渠道断面各点对应的基土自由冻胀变形w0( )

x为

式中：H为基土的冻结深度。

在土体冻胀过程中，当冻胀变形完全释放时，不会产生冻胀力，当自由冻胀变形被完全约束时，即被约束的冻胀变形为w0时，将产生最大的冻胀力，可表示为[22,25,27]

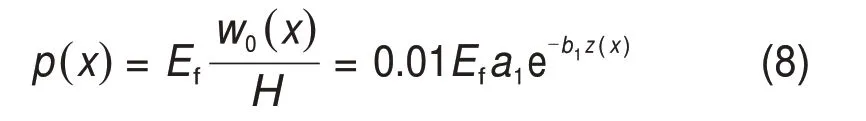
式中：Ef为冻土弹性模量。

但在实际的冻胀变形过程中，冻胀变形既不可能被完全约束，也不可能完全释放，被约束的冻胀变形可表示为w0(x)-w(x)，w(x)为衬砌各点实际的冻胀变形，则衬砌各点实际的冻胀力为

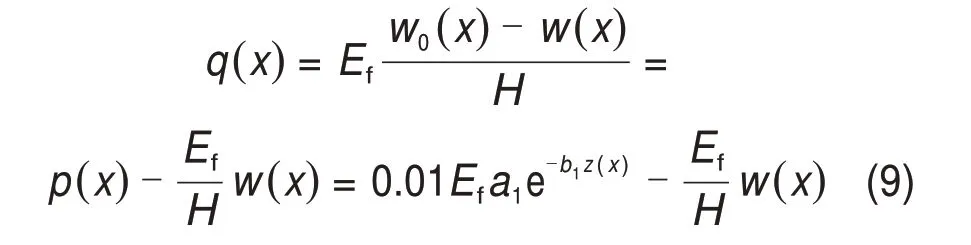
在冻胀力作用下，衬砌板会发生一定的弯曲变形，使衬砌与土体接触的界面发生一定的横向位移，同时由于底部衬砌的上抬作用，坡板衬砌会产生一定的切向位移。但是，相对于冻胀作用下衬砌的切向位移，弯曲变形引起的界面横向位移可忽略不计。梁与基土之间的冻结力(摩阻力)主要由衬砌的相对切向位移引起。通常构筑物与冻土界面的冻结力与土体的温度、含水率、剪切速率和法向压力(本文中的冻胀力)等多因素相关[6,28]。在极限状态下，根据界面的摩尔−库仑剪切强度准则，切向冻结力与法向力的关系可表示为[29−30]

式中：c为界面的黏聚力；f为界面的摩擦因数。将式(9)代入式(10)可得

对式(11)求导，可得

将式(9)和式(12)代入式(5)，可得

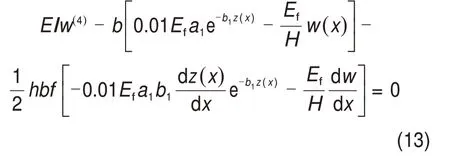
整理式(13)后可得衬砌板在冻胀力和冻结力作用下的挠曲线微分方程为

式(14)为四阶常系数非齐次微分方程，其解由通解和特解组合构成，其特征方程可表示为

根据计算模型中的参数，式(15)存在一对共轭形式的负根，因此，式(14)对应的齐次方程的通解为

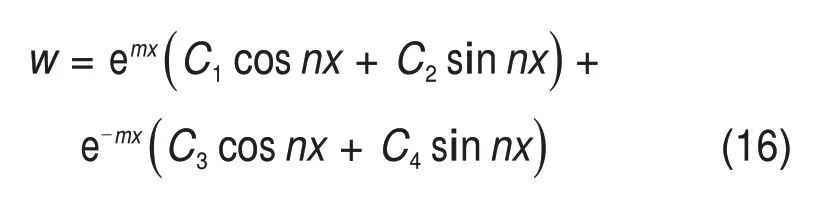
式中：C1，C2，C3和C4为任意系数；m和n为特征方程的特征系数。

根据式(14)中非齐次项的形式，式(14)的特解形式可由下式给出[31]：

式中：Q(x)为与非齐次项形式有关的多项式；t和s为与非齐次项形式有关的系数。

对于底板，衬砌各点与地下水位的距离为常数，因此，非齐次项为常数，令w*=A0，并代入式(14)，可得

则底板衬砌挠曲线微分方程的特解为

对于坡板衬砌，不同计算位置与地下水位距离不同，非齐次项为x的函数，因此，令w*=e-b1(z0+xsinθ)，并代入式(14)，可得

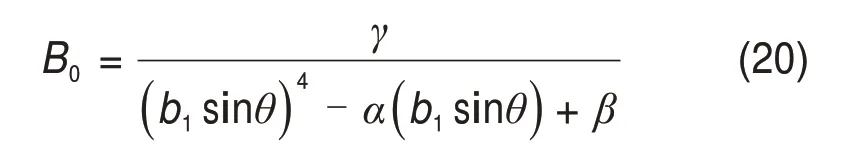
则坡板衬砌挠曲线微分方程的特解为

受渠道结构形式的影响，在渠基土冻胀变形过程中，冻结初期渠道顶部先冻结产生冻胀变形，底部尚未发生冻胀变形。随温度降低，渠道顶部的冻胀变形逐渐放缓或停止，底部的冻胀变形逐渐增大。由于渠道底部距离地下水位较近，因此，最终底部的冻胀变形比顶部的变形大。根据以上的衬砌的变形过程和工程实践经验及已有的研究成果，假设渠坡和渠底为简支梁[4,18,20−22]。因此，对于渠道坡板和底板，其边界条件都可表示为

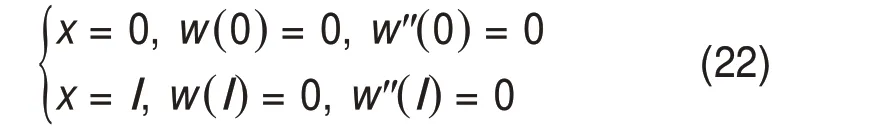
通过上述边界条件，可以分别计算得到渠道坡板和底板挠曲线微分方程所对应的解的4个系数C1，C2，C3和C4。

渠道坡板和底板任意横截面的弯矩和剪力可通过下式计算：

2 工程案例

肖旻[9]对新疆塔里木灌区一处梯形混凝土衬砌渠道进行了现场试验，监测了渠道现场的气温、地温、冻深、降水量及衬砌板的冻胀变形。同时肖旻等[22]采用不考虑切向冻结力时的弹性地基梁模型对此渠道衬砌的变形进行了分析，本文以此渠道为工程案例进行分析计算，并与肖旻等[22]的研究结果进行比较，以验证本文解析解的正确性。

2.1 工程概况

新疆塔里木灌区以阿拉尔市为中心，年最低气温为−29.3～−24.0 ℃，目前已修建成各类灌溉渠道长度约为2 300 km，灌区地表水丰富，地下水为河流两岸嵌入式淡水体，地下水埋深较浅，渠道衬砌存在严重的冻胀破坏[9]。由于此类寒旱地区降雨量较小且地下水埋深较浅，引发基土冻胀的主要水分来源为地下水补给。

灌区一典型梯形混凝土衬砌渠道断面尺寸如图3所示。该渠道为现浇C15混凝土衬砌，渠坡和渠底的冻土层冬季最低温度分别为−14.7 ℃和−9.4 ℃。本例中冻土弹性模量按冬季冻土层最低温度取值，渠底冻土层弹性模量约为2.35 MPa，渠坡冻土弹性模量约为2.61 MPa[22]。渠道基土的冻结深度约为1 m，地下水位距离渠底约为1 m。

图3 原型渠道断面示意Fig.3 Schematic diagram of canal section

2.2 计算结果与对比分析

选取坡板和底板宽度为1 m，根据已有研究选取a1和b1分别为15和1[25]，对衬砌各点冻胀位移进行计算和对比分析。图4 所示为不考虑摩阻力时，按本文解析解法得到的底板和坡板衬砌的变形曲线与现场实测数据[9]和肖旻等[22]计算得到的变形曲线的对比图。由图4可以看到：本文的计算结果与实测值和肖旻等[22]所得计算值均有较好的一致性，验证了本文解析解的正确性。渠道坡板和底板两端的观测值并不为0，而衬砌板计算模型中两端挠度假设为0，这与实际观测值存在一定误差，但偏差较小，仍可满足工程需求。

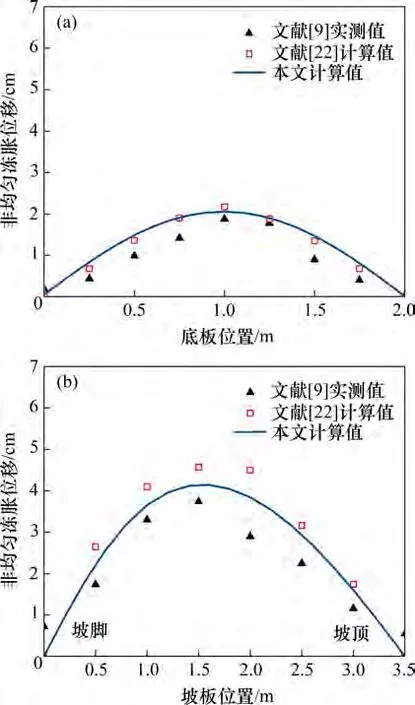
图4 本文计算值与实测值和已有计算值对比Fig.4 Comparisons of results in this study with existing experiment and calculation

对于开放系统渠道，不同的地下水位埋深对渠道的冻胀位移影响显著，因此，假定地下水位分别为0.5，1.0，1.5 和2.0 m，对渠道底板和坡板的冻胀变形和内力进行计算分析，此外，在分析底板衬砌的变形和内力时不考虑界面冻结力(摩阻力)的影响。图5 所示为不同地下水位埋深时底板的冻胀位移、弯矩和剪力。从图5可以看出：随地下水埋深增加，最大冻胀变形、最大弯矩和最大剪力明显下降。当地下水埋深由0.5 m 增至2.0 m时，底板衬砌最大冻胀变形由3.4 cm 降至0.7 cm，降低了79%，表明控制地下水位是防治渠道冻胀破坏的有效手段之一，在实际工程中也经常在渠道底部设置排水暗渠和排水井以降低渠道的局部地下水位[6]。由于未考虑渠道两侧渠坡的阴阳坡效应，底板渠道的变形和内力都是对称分布的。

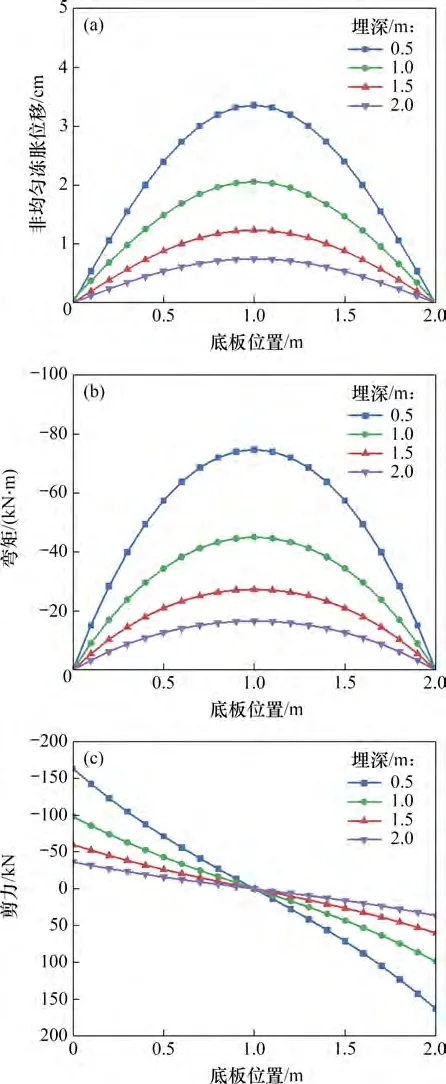
图5 不同地下水埋深时底板衬砌的计算结果Fig.5 Calculation results of bottom lining with different groundwater depths

图6 所示为不同地下水位时坡板的冻胀位移、弯矩和剪力的变化。从图6可以看出：随地下水埋深增加，最大冻胀位移、最大弯矩和最大剪力均明显下降。当地下水埋深相同时，由于坡板不同位置与地下水位的距离不同，使作用于坡板不同位置的冻胀力不同，因此，冻胀位移、弯矩和剪力沿坡板均呈非对称分布。最大冻胀位移发生在距离坡脚43%坡板长度处，最大弯矩发生在距离坡脚25%坡板长度处，这与已有的研究成果中梯形渠道衬砌破坏主要发生在距离渠坡坡脚25%～45%坡板长度处的结果吻合[22]。

图6 不同地下水埋深时坡板衬砌的计算结果Fig.6 Calculation results of slope lining with different groundwater depths

图7所示为考虑不同界面摩擦因数时坡板衬砌的冻胀变形、弯矩和剪力的变化。从图7 可以看出：不同摩擦因数对冻胀变形和剪力的影响较小，但对弯矩有一定影响，随摩擦因数由0 增至0.7，最大弯矩由36.3 kN·m 增至40.8 kN·m，增大了12.4%。这是因为水平摩阻力的作用相当于在衬砌板上增加了偏心拉压荷载，其弯矩有叠加作用[32]。因此，在设计高寒区渠道衬砌时，只考虑衬砌的刚度的情况下，可不考虑界面冻结力的影响。但当要重点考虑衬砌的强度时，应该考虑界面冻结力的影响。

图7 不同界面摩擦因数时坡板衬砌的计算结果Fig.7 Calculation results of slope lining with different interface friction coefficients

2.3 渠道衬砌冻胀破坏判断准则

导致渠道混凝土衬砌结构发生冻胀破坏的原因包括法向冻胀位移过大导致衬砌板发生鼓胀和隆起，衬砌板局部弯矩过大而导致强度破坏使衬砌板产生裂缝甚至折断，以及衬砌结构法向冻胀位移过大引起衬砌稳定性降低，导致衬砌板架空乃至滑塌。由于构成渠道衬砌结构的混凝土类材料抗拉强度较低，渠道衬砌板经常因为局部弯矩过大而导致开裂，这一方面降低了渠道衬砌板的抗弯刚度，另一方面导致水分渗漏的增强而使衬砌板的冻胀破坏加剧，使衬砌板陷入“冻胀开裂—渗漏—更严重的冻胀开裂”的恶性循环中，最终造成衬砌结构的彻底破坏。由此可见，渠道衬砌板内界面拉应力达到极限抗拉强度使衬砌板开裂是渠道衬砌结构破坏的触发标志。因此，可以通过控制衬砌板中裂缝的产生来避免渠道结构发生冻胀破坏，即通过对衬砌板中最容易发生冻胀破坏的界面进行抗裂验算来建立渠道衬砌结构的冻胀破坏判断准则[22]，计算公式如下：

式中：σmax为界面最大拉应力；E为衬砌板弹性模量；[ε]为许用拉应变。

按照图4所示实际变形特征，取横截面最大弯矩为40 kN•m，计算得到的应变为0.001 7，比普通混凝土的许用拉应变(0.000 15)大，衬砌板会在最大弯矩处会出现裂缝。而根据现场观察，原型渠道在坡板下部有部分渠道出现冻胀破坏，产生不规则纵向裂缝[9]。纵向裂缝的产生可释放部分内力，使衬砌板在当年冬季不会产生较大的破坏。但在多年运行后，裂缝逐渐累积，最终会导致衬砌发生破坏。

为避免渠道衬砌冻胀位移过大导致的膨胀、隆起甚至架空、滑塌，SL 23—2006“渠系工程抗冻胀设计规范”[33]中以衬砌许用法向位移作为衬砌冻胀变形和抗冻胀稳定性的控制标准，即

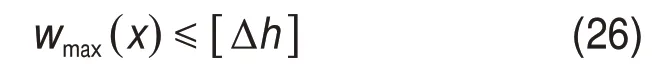
式中：wmax为最大变形量；[Δh]为许用冻胀变形。

从图5和图6可以看出：对于坡板，地下水埋深大于2 m 的坡板冻胀变形比许用变形(2 cm)小，对于底板衬砌，地下水埋深大于1 m的底板冻胀变形比许用变形小。通过渠道的刚度特征综合判断，此处渠道的下水埋深需控制在2 m以上可保证渠道冻胀变形处于安全范围内。

在本文所建立的衬砌冻胀破坏力学模型中，仅考虑了衬砌和基土的弹性变形，并未考虑其塑性变形及衬砌微裂纹发展过程等因素对冻胀力的消减作用，因此，计算得到的内力偏大。此外，实际工程中衬砌的两端仍有冻胀发生，将衬砌两端假设为铰支座与实际工程有差异，但考虑梁顶和梁底冻胀变形的产生不同步的特征，根据工程实践经验，两端简化为铰支座形式仍然能够满足分析要求。

3 结论

1)考虑衬砌与基土界面的冻结力与作用于衬砌板的冻胀力的相互关系，建立考虑界面冻结力作用的弹性地基梁模型，并得到了模型的解析解。

2)坡板最大冻胀位移发生在距离坡脚43%坡板长度处，最大弯矩发生在距离坡脚25%坡板长度处，这与已有的研究成果中梯形渠道衬砌破坏主要发生在距离渠坡坡脚25%～45%坡板长度处的结论吻合。

3)当考虑界面冻结力时，冻结力对挠度和剪力影响很小，而对弯矩的影响较大。在摩擦因数由0 增至0.7 时，最大弯矩增大了12.4%。界面的冻结力相当于作用于梁上有偏心拉压荷载，其弯矩有正叠加作用。因此，在衬砌设计过程中，当仅考虑衬砌的刚度时，可不考虑冻结力的影响；但当重点考虑衬砌的强度时，应考虑界面冻结力的影响。