爆破载荷下岩石的拉压损伤模型

王卫华，张恒根，李夕兵

(1.中南大学资源与安全工程学院，湖南长沙，410083 2.中国海洋大学环境科学与工程学院，山东青岛，266100)

岩石在爆破载荷下的损伤与断裂是一个复杂的动态演化过程，为了探究这一过程，学者们基于不同的理论相继建立了有关的爆破损伤模型。如GRADY 等[1]假定岩石中均匀分布的内在裂纹在拉应力下被激活，且被激活的裂纹数目服从双参数的韦伯分布，由单位体积被激活的裂纹数目定义损伤变量进而描述岩石刚度的降低量，提出了岩石各向同性拉伸损伤的GK 模型。TAYLOR 等[2]在GK 模型的基础上，引用BUDIANSKY 等[3]使用自洽法得到的岩石弹性参数表达式，结合GRADY等[1]给出的岩石动态断裂块度的计算公式，将损伤定义为由裂纹发展导致的失去承载能力的岩石体积分数，建立了损伤变量与裂纹密度、有效泊松比及有效体积模量之间的关系式，并将其耦合到岩石的通用线弹性本构中，得到了TCK 模型。KUSZMAUL[4]保留了GK模型中关于裂纹激活率和裂纹平均尺寸的研究成果，同时考虑了高密度微裂纹周围应力释放区的材料重叠，在裂纹的激活率中考虑损伤减小，对裂纹密度的表达式进行了修正，通过沿用TCK 模型中对岩石参数的处理关系，提出了KUS 模型。THORNE 等[5]在模拟过程中注意到材料随时间逐渐劣化的过程和模型在大裂纹密度条件下的适应性，通过不同的损伤变量定义方法，在上述3 种模型的基础上提出了THORNE模型。YANG等[6]将岩石单元点上的总拉伸应变定义为3个对数主拉伸应变的总和，同时假定岩石的脆性破坏由总拉伸应变控制，以经验巴黎定律的形式模拟裂纹密度的增长，提出了包含损伤累积和荷载率依赖性的YANG 模型。LIU 等[7]在YANG 模型的基础上，以体积拉伸应变确定裂纹是否发展和激活，将损伤定义为给定裂纹密度下的断裂概率，考虑动能与表面能之间的平衡、加载率和材料刚度损伤的影响给出了爆破块度的计算公式，提出了LIU模型。YANG和LIU模型均假定岩石损伤过程中泊松比不变，且分别给出了总拉伸应变和体积拉伸应变的临界值，用于区分岩石的脆性破坏和压缩屈服模式。

上述模型为经典的岩石爆破损伤模型，其他学者或在经典模型的基础上，或基于分形、逾渗等理论，或借助有限元分析软件对岩石的爆破损伤模型进行了进一步研究，如：胡英国等[8]将5 种经典的爆破损伤模型导入LS-DYNA中进行了比较与改进；陈俊桦等[9]考虑了岩石完整程度对爆破效果的影响，对YANG模型进行了改进；谢福君等[10]结合经典岩石冲击损伤模型和统计损伤力学理论，提出了岩石的拉、压统计损伤本构模型；杨仁树等[11]根据盒维数的计算原理，建立了分形维数与爆破损伤度之间的对应关系；张我华等[12]通过定义损伤张量，建立了各向异性的岩石损伤模型；梁瑞等[13]将TCK模型导入LS-DYNA中对边坡台阶爆破进行了数值模拟。爆破损伤理论问题一直是爆破理论发展的前沿问题，以往学者对于爆破损伤模型的研究极大地促进了爆破理论与技术的发展和完善。

现有的爆破损伤模型多将爆破前的岩石视为无损状态，忽略了岩石存在的初始损伤的影响，而初始损伤在很大程上控制着岩石的破碎过程[14]。其次，现有模型大都仅考虑了岩石在体积拉伸条件下的损伤响应，而在体积压缩时多采用未考虑损伤的理想化弹塑性本构，这与实际情况不符，且现有模型多将岩石中微裂纹的分布理想化，忽略了微裂纹引起的各项异性损伤，较少考虑爆生气体对岩石的损伤和破坏作用。为了更完整地描述岩石在爆破载荷下的损伤演化过程，本文从现有模型的不足之处入手，根据岩石在动态拉压应力下不同的响应特征，考虑岩石的初始损伤，提出了基于LIU 模型改进的动态拉损伤模型和基于MOGI-COULOMB 屈服准则的动态压损伤模型。利用提出的模型对爆破损伤进行数值模拟，并将模拟结果与其他爆破损伤模型的模拟结果和现场实测结果进行对比分析，以验证所提出模型的合理性。

1 拉压损伤模型的建立

1.1 基于LIU模型改进的拉损伤模型

LIU 等[7]假定岩石的脆性破坏由体积拉伸应变引发和控制，认为只有当体积拉伸应变大于临界拉伸应变时，岩石中的裂纹才会生长和成核，进而降低岩石的刚度。LIU 模型相较于TCK 模型可以更全面地解释岩石的脆性破坏模式，因此，选取LIU模型作为拉损伤的拟改进模型。

未考虑初始损伤时，在给定的应力水平和应力持续时间内，岩石单位体积的裂纹密度Cd1可以表示为[7]

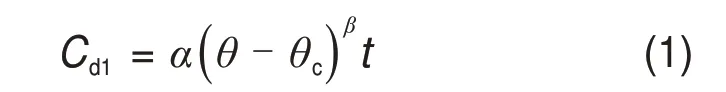
式中：α和β为岩石材料常数；t为时间；θ为体积应变；θc为临界拉伸体积应变。体积应变θ计算式为

式中：εi为i方向主应变；体积应变θ>0表示体积拉伸，θ<0表示体积压缩。

式(1)可以用微分形式写成

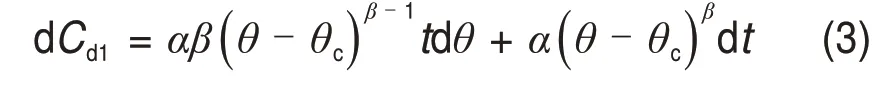
对式(3)积分可得增量形式的裂纹密度表达式为

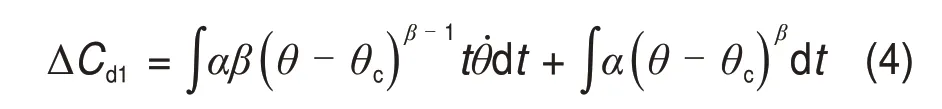
式(4)反映了裂纹密度增量不仅与给定时间dt内的应变有关，而且与给定应变水平下的体积应变率̇有关。

考虑岩石内存在的初始损伤，假定当初始损伤存在时，LIU 模型中裂纹密度的表达式形式不变，有

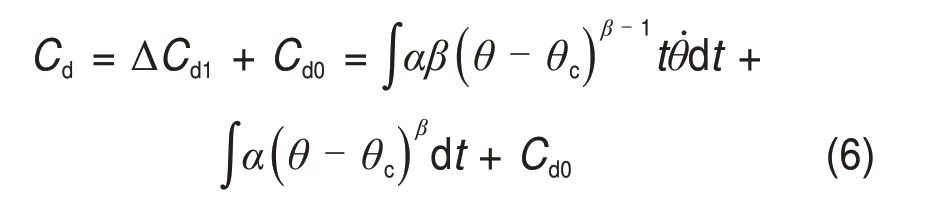
式中：Cd0为单位体积岩石的初始裂纹密度；Cd为考虑初始损伤时岩石单位体积的总裂纹密度。

假定岩石为连续、均匀的各向同性材料，根据统计断裂力学，岩石的拉伸损伤变量Dt为给定裂纹密度下的断裂概率[7]：

当ΔCd1=0 即Cd=Cd0时，单位体积岩石的初始损伤D0计算式为

需要指出的是，无损岩石在自然界中几乎不存在。在工程应用中，通常将完整性高的岩块视为无损岩石，岩体的初始损伤D0可以由爆破前松散岩体较完整岩块的声速变化得出[15−16]：

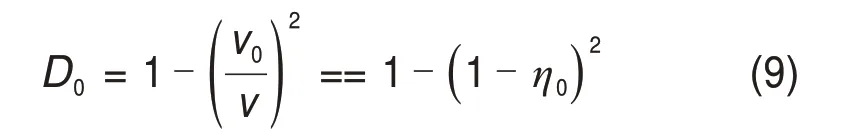
式中：v为岩块中的声速；v0为岩体中的声速；η0=(v-v0)/v，为爆破前岩体较岩块的初始声速降低率。

根据LEE等[17]提出的应变余能等效假说，假定岩石为各向同性材料且处于弹性阶段时，损伤导致的岩石单元刚度劣化的关系式为

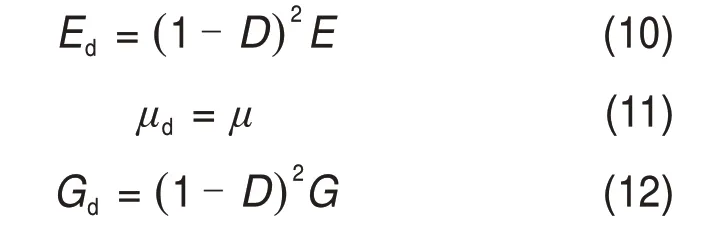
式中：Ed，μd和Gd分别为损伤岩石的有效弹性模量、有效泊松比及有效剪切模量；E，μ和G分别为无损岩石的弹性模量、泊松比以及剪切模量；D为相较于无损岩石的损伤变量。

从式(10)～(12)可以看出，在应变余能等效的假设下，损伤岩石的有效弹性模量和有效剪切模量均为无损岩石的(1−D)2倍，这与基于LEMAITRE等效应变假说所得的结论不同。损伤岩石的泊松比没有改变，根据JAEGER等[18]的结论，泊松比的变化取决于裂纹的形状，若材料中包含平整开放的裂纹或等尺寸的空腔，则其有效泊松比小于其固有泊松比，若材料中的裂纹为闭合裂纹，则其有效泊松比大于固有泊松比；假定在拉伸损伤期间，每一种类型的裂纹均等产生，由此可以认为损伤岩石的泊松比不变。根据YANG 等[6]的结论，若泊松比不变，则损伤岩石弹性参数之间的关系不会改变。

由式(10)和(12)可得岩石单元的初始弹性模量E0和初始剪切模量G0计算式为

由式(10)，(12)～(14)可得由初始弹性模量和初始剪切模量表示的弹性模量和剪切模量拉伸损伤劣化的公式为

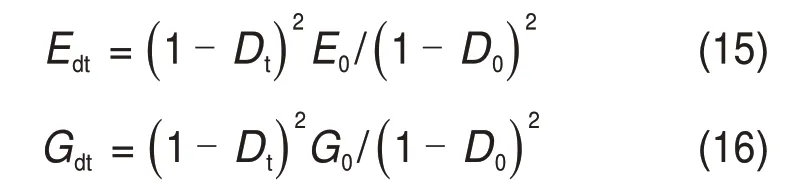
式中：Edt和Gdt分别为受拉伸损伤后岩石的有效弹性模量和有效剪切模量。

岩石的宏观弹性常数满足下式[12]

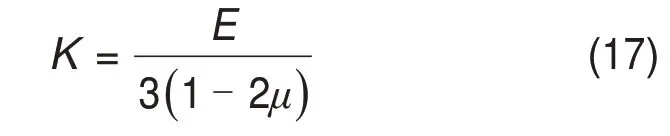
式中：K为无损岩石的体积模量。

由于假定损伤岩石弹性参数间的关系不变，由式(15)和(17)可得由初始体积模量K0表示的岩石体积模量拉伸损伤劣化的表达式为

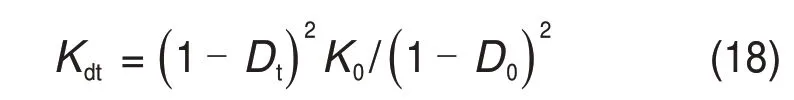
式中：Kdt为受拉伸损伤后岩石的有效弹性模量。

由于岩石为脆性材料，其抗拉强度远小于抗压强度，因此，可以认为岩石在受拉损伤直至破坏的整个阶段内均处于弹性阶段。将拉伸损伤劣化的弹性模量和剪切模量耦合到由广义胡克定律得到的岩石线弹性应力−应变关系中，可得岩石拉伸损伤的应力−应变本构为

式中：σij为应力张量；εij为应变张量；εkk=ε11+ε22+ε33；δij为Kronecker 符号；λdt为拉伸损伤后的拉梅常数，其计算式为[6]

将应力和应变张量分解为偏量形式，上述拉伸损伤本构可以表示为

式中：θ>θc；P为体应力；Sij为偏应力张量；eij为偏应变张量。

1.2 基于MOGI-COULOMB准则的压损伤模型

当θ>θc时，岩石材料的破坏在微观上表现为岩石中均匀分布的微裂纹在拉应力作用下的成核、扩展，在宏观上表现为弹脆性破坏。在拉伸损伤开始直至破坏的整个阶段内，岩石微元满足由式(21)定义的包含初始损伤和拉伸损伤的线弹性本构关系。当θ≤θc时，若岩石材料未发生屈服(等效塑性应变εˉp=0)，则此时岩石微元满足只包含初始损伤即D=D0的线弹性本构关系，该关系以应力和应变的偏量形式表示为

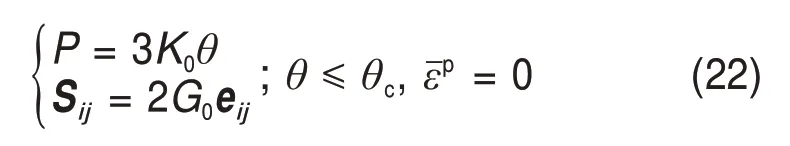
若岩石材料发生屈服乃至破坏，则该破坏在宏观上表现为岩石在压应力作用下的塑性流动破坏，此时，岩石微元满足包含初始损伤和压缩损伤的弹塑性本构关系。从主应力空间看，当θ≤θc时，岩石中1点的应力状态经过不同的压缩加载路径，到达屈服面后，岩石材料产生塑性流动。当塑性流动产生时，压缩损伤即开始产生，并且伴随塑性流动而增长，压缩损伤的增长也将反过来影响岩石材料的塑性流动。

岩石材料发生屈服后，其应力与应变的关系不再一一对应，作为内变量的塑性应变，可以较好地反映其加载历史和加载路径，采用等效塑性应变εˉp表征岩石材料压缩损伤变量的演化过程。压缩损伤变量Dc被定义为等效塑性应变的指数函数，等效塑性应变计算式[19]为

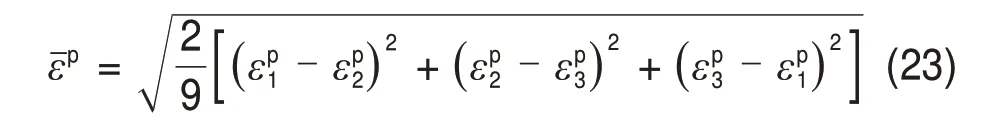
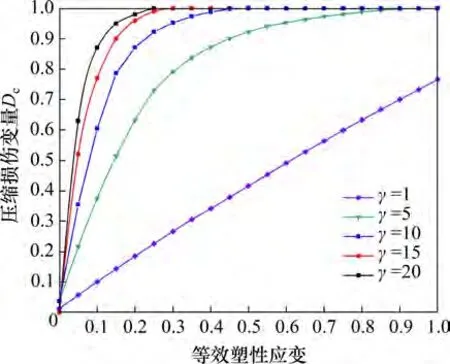
图1 压缩损伤变量与等效塑性应变的演化关系[19]Fig.1 Evolution relationship between compressive damage variable and equivalent plastic strain[19]

以往学者对岩土等材料基于应力空间中的屈服问题进行了大量研究[20−22]，提出了各种不同的屈服准则，目前应用较广的屈服准则有MOHRCOULOMB 屈服准则、HOEK-BROWN 屈服准则和DRUCKER-PRAGER 屈服准则等。文献[23]基于大量实验数据对MOGI准则进行了修正，将其与COULOMB 准则相结合，提出了以岩石抗剪强度参数(黏聚力c和内摩擦角φ)表示的MOGICOULOMB屈服准则。该准则在π平面上的投影为外接MOHR-COULOMB 强度准则的曲边六边形[20]，如图2所示，在轴对称的三轴拉伸和压缩状态时二者重合。MOGI-COULOMB 准则考虑了中间主应力Σ2对岩石强度的影响，且其参数物理意义明确，便于实验确定，可以更好地描述真三轴条件下岩石材料破坏的强度特征，得到了国际岩石力学协会的推荐[24]。

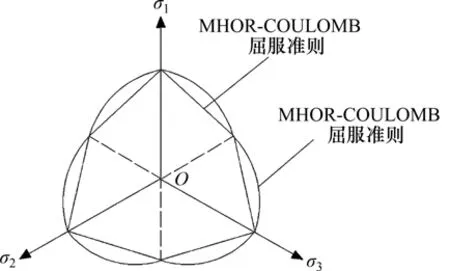
图2 π平面上MOGI-COULOMB屈服准则曲线Fig.2 MOGI-COULOMB yield criterion curve in π plane

本文基于MOGI-COULOMB 屈服准则建立岩石的弹塑性压缩损伤本构模型。 MOGICOULOMB强度准则表示为[20]

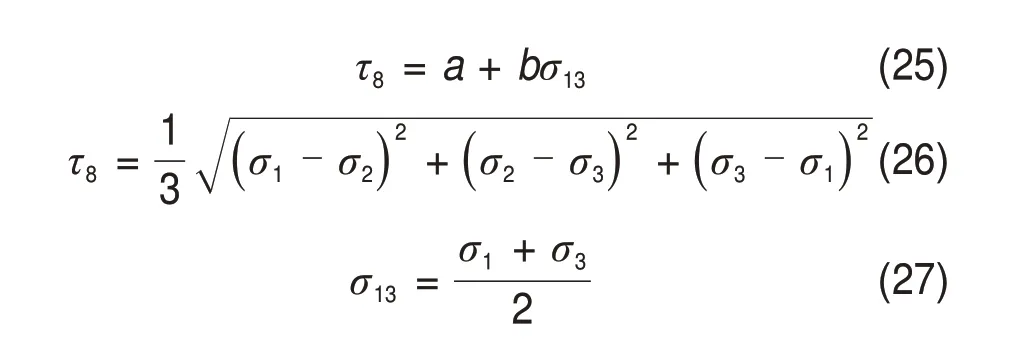
式中：τ8为八面体剪应力；σ1，σ2和σ3为第一，第二和第三主应力，σ1>σ2>σ3；σ13为作用在剪切面上的平均有效正应力；a和b为与岩石力学性质有关的材料常数，可在常规三轴下由MOGI-COULOMB准则与MOHR-COULOMB准则联合得出[20]。

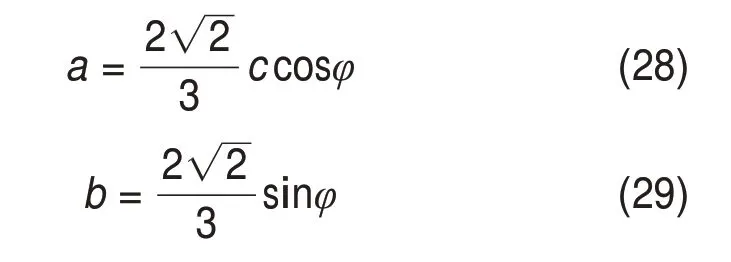
将压缩损伤引入屈服准则中，则基于MOGICOULOMB 屈服准则，考虑压缩损伤效应的弹塑性屈服函数和塑性位势函数可以表示为

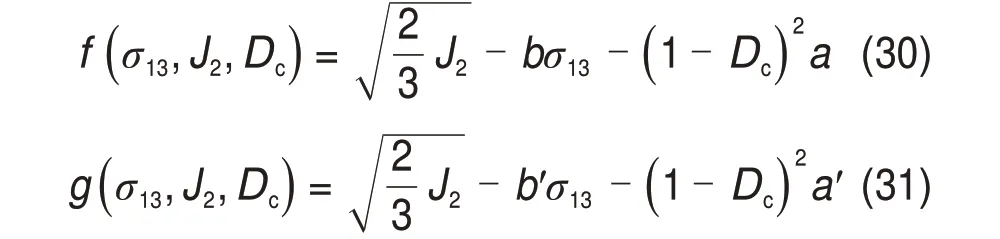
式中：a'和b'均为材料常数；J2偏应力的第二不变量。a'，b'和J2的计算公式为[20]

式中：ψ为岩石的膨胀角。由式(10)，(12)～(14)和(17)可得由初始弹性模量、初始剪切模量和初始体积模量表示的弹性模量、剪切模量和体积模量压缩损伤劣化的关系式为

式中：Edc，Gdc和Kdc分别为受压缩损伤后岩石的有效弹性模量、有效剪切模量和有效体积模量。

岩石材料产生塑性变形时的应变增量dεij可以分解为塑性应变增量和弹性应变增量个部分，即[21]

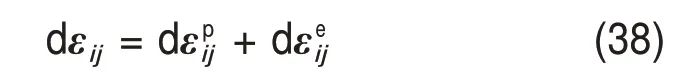
其中，弹性应变增量满足包含初始损伤和压缩损伤的胡克定律，为

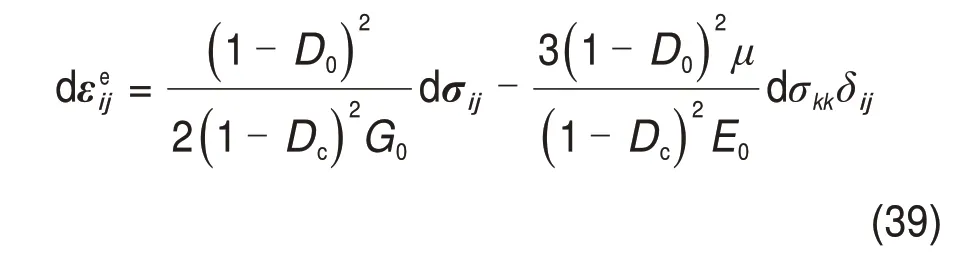
式中：dσij为应力增量；dσkk=dσ11+dσ22+dσ33。

塑性应变增量由与加载条件相关联的流动法则给出。当φ=ψ，即f(σ13，J2，Dc)=g(σ13，J2，Dc)，此时为关联的流动法则。塑性应变增量计算式为

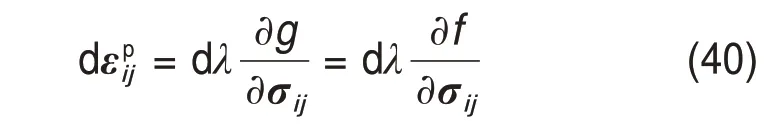
式中：dλ为非负的塑性因子，其值由一致性条件确定。根据上述推导，总应变增量为

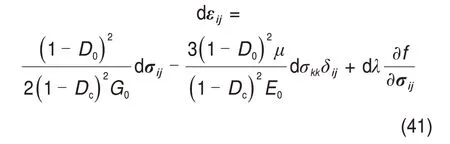
假定岩石材料满足如下加卸载准则[20]：

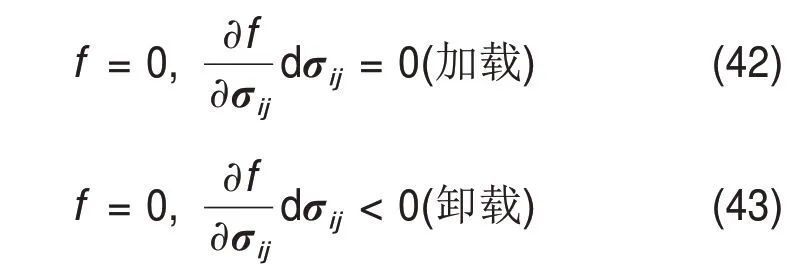
理想弹塑性材料满足一致性条件，当产生塑性变形时，应力点一直处于屈服面上，即[20]

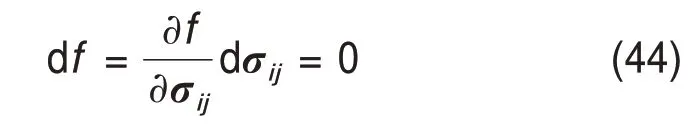
将式(44)代入式(41)即可解出dλ。本文将岩石视为理想弹塑性材料，暂不考虑应变硬化的影响。

考虑到塑性应变的球张量为0，理想弹塑性材料增量形式的本构可以写为

1.3 损伤阀值的确定

由于工程应用目的和对损伤变量的定义方式不同，用以确定爆破损伤影响范围的判据即损伤阀值Df的取值也不尽相同，如GRADY 等[1−2,4]基于各自定义的损伤模型，均将Df取为0.2。YI 等[25]和LIU 等[26]基于RHT 模型进行数值模拟时，将Df分别取为0.60 和0.22。胡英国等[8,27]基于爆破前后岩石声速的衰减特征，将Df取0.19。李新平等[28]采用爆破质点振动速度作为损伤判据，Df取0.18。以上研究均将Df的取值确定为一定值，但在实际工程爆破中，Df的取值与岩石初始的物理性质参数有关。

损伤变量和声波波速的关系如下[15−16]：

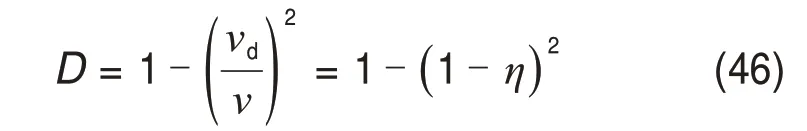
式中：vd为爆破后受损岩体中的声速，vd≤v0≤v；η为vd相较于爆前无损岩块中声速v的降低率。

根据PL/T 5389—2007“水工建筑物岩石基础开挖工程施工技术规范”的规定，采用钻孔声波观测法判断工程岩体是否受爆破影响。当同部位岩体的爆后声速相较于爆前无损岩块中声速的降低率η大于15%时，即认为爆破对该处岩石有影响。采用η≥15%作为岩体受爆破损伤影响的判据，由式(9)和式(46)可得以初始损伤表示的损伤阀值的表达式为

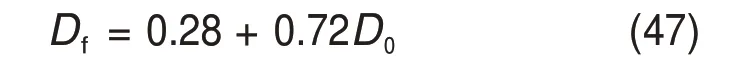
由式(47)确定的损伤阀值与岩石的初始损伤值有关，这与LIU 等[7,9]得出的结论相符。当岩石的损伤值满足D≥Df或D≥D0时，可分别判定岩石受爆破影响或产生损伤[9]。

1.4 模型参数确定

在拉伸损伤模型的构建过程中，确立了3个材料常数α，β和θc。在进行岩石材料的单轴静态拉伸实验时，在拉伸应力未达到岩石的静态强度之前，岩石一直处于弹性阶段，不会产生损伤与破坏；当拉伸应力达到岩石的静态强度时，随着应力增加，岩石的损伤不断累积并伴随刚度劣化直至破坏。因此，岩石的临界体积拉伸应变θc可以由岩石的静态强度衡量，当岩石包含初始损伤时，θc计算式为[7]

式中：Sc为岩石的静态强度。

岩石在爆破载荷下处于三维的应力状态，当1个应力主方向上表现为压应力时，另外2个应力主方向上通常表现为拉应力；当1个应力主方向表现为拉应力时，另外2个应力主方向上则表现为压应力。式(2)为3个主应变的计算式，计算时，2个符号相反的应变分量会部分抵消，因而，其描述了3个主应变方向上的平均体积变化。

定义岩石断裂时的应力，体积应变和裂纹密度分别为σf，θf和Cdf。由式(48)可得

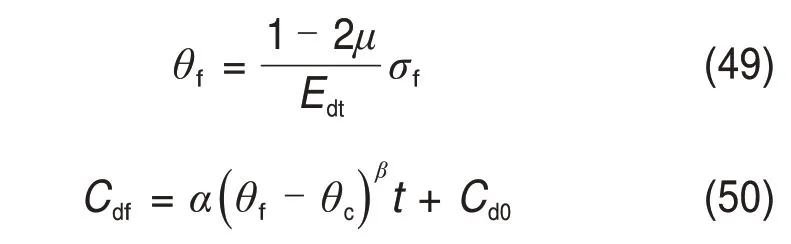
假定应变率θ̇恒定，则达到临界体积应变θc所需的临界时间tc为[7]

将关系式θf=̇(tc+t)和式(51)代入式(50)，求解时间t，可得

将式(15)，(51)～(52)和(48)以及关系式θf=θ̇(tc+t)代入式(49)，可得断裂应力σf与应变率θ̇的关系为

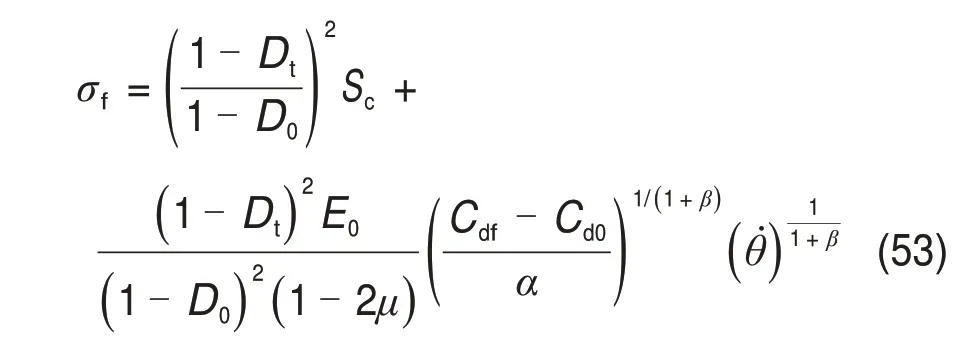
由式(53)可知参数β为确定断裂应力的应变率依赖性的材料常数。以往研究表明，对于岩石等脆性材料，动态断裂应力高于其静态强度并取决于应变率的立方根，为满足这一点，将β取2。在裂纹密度函数中，参数α以描述在特定应变水平下微裂纹的成核过程，当岩石的初始损伤D0以及在给定应变率θ̇下的断裂应力σf已知时，将式(7)～(8)和式(47)代入式(53)可得参数α的计算公式为

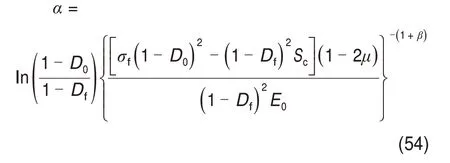
2 模型验证

文献[9]考虑岩体的完整程度对YANG 等[6]的爆破损伤模型进行了改进，将改进后的模型引入LS-DYNA 数值软件中，对溪洛渡水电站地下开挖工程实例进行数值模拟，并将数值模拟结果与现场实测结果和基于常用的TCK 损伤模型的模拟结果进行对比，取得了较好的效果。本文采用文献[9]中的工程应用实例，按照其给出的岩石力学参数、几何尺寸和炸药参数等进行建模，将本文所建立的拉压损伤模型导入数值模型进行爆破加载，以验证本文所建立模型的适用性。

2.1 材料模型及参数

2.1.1 炸药材料模型及参数

采用LS-DYNA 中内置的*MAT_HIGH_EXPLOSIVE_BURN高能炸药模型模拟工程中使用的2 号岩石乳化炸药，采用JWL 状态方程描述爆轰产物体积与压力的关系[29]，JWL状态方程为

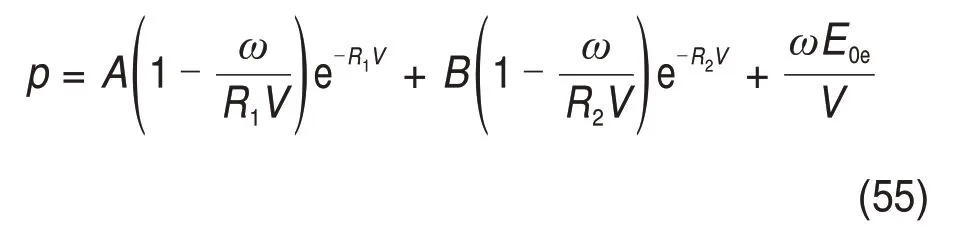
式中：A，B，R1，R2和ω均为材料常数；p为爆轰压力；V为爆轰产物体积与未爆轰炸药体积之比；E0e为单位体积炸药介质的初始内能。

2 号岩石乳化炸药的材料参数如表1 所示[9]，其中，ρe为炸药密度，u为爆速。

表1 炸药材料参数Table 1 Eplosive material parameters

2.1.2 空气材料模型及参数

采用关键字为*MAT_NULL的空物质材料模型模拟空气，空气材料的热动力学性质使用*EOS_LINEAR_POLYNOMIAI 状态方程表征[29]，其线性多项式的状态方程为

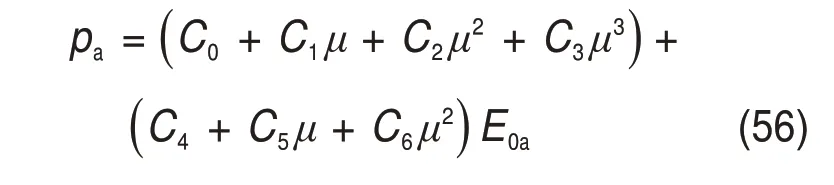
式中：pa为空气压力；μ为比体积；C0～C6为材料常数；E0a为单位体积空气介质的初始内能。

空气的材料参数如表2所示[9,30]，其中，ρa为空气密度。

表2 空气材料参数Table 2 Air material parameters

2.1.3 岩石材料模型及参数

工程实测地的开挖基岩为坚硬玄武岩，对于岩石单元，采用本文确定的拉压损伤本构关系。岩石材料的力学参数取值如表3 所示[7,9,30]，其中，ρc为岩石密度。

表3 岩石材料参数Table 3 Rock material parameters

2.2 数值计算模型

考虑模型的对称性，采用文献[9]中的几何尺寸，建立外观为1/4圆柱体的三维计算模型，模型的几何尺寸如图3所示。图中圆柱高为10.0 m，半径为10.0 m，采用径向不耦合，轴向耦合装药。药卷半径为35.0 mm，炮孔半径为45.0 mm，装药长度为2.5 m，堵塞长度为2.0 m。为方便计算，堵塞段定义为岩石。采用流固耦合算法，孔底起爆，圆柱上底面设置为自由边界，长方形的两侧面设置为对称边界，圆弧侧面和下底面设置为无反射边界。

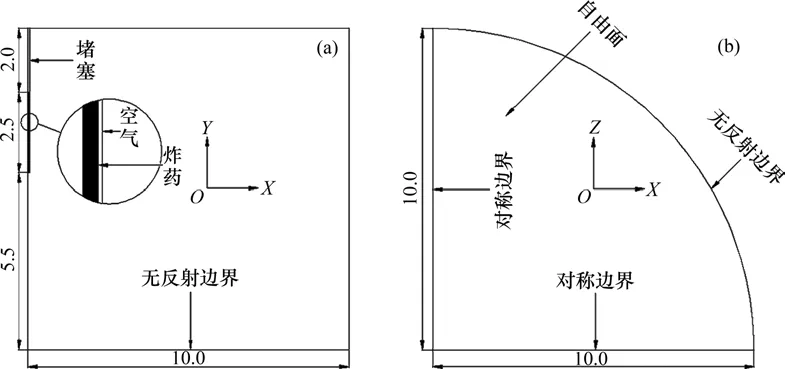
图3 计算模型示意图Fig.3 Calculation model diagrams

2.3 结果及分析

2.3.1 基于拉压损伤模型的数值计算结果分析

本次计算所需设置的初始损伤由现场测试的孔口自由面到孔底岩石的平均声波波速确定，现场实测得到的初始损伤D0为0.4。设置初始损伤D0为0.4 时的爆破损伤分布如图4 所示，其中，损伤满足D0≤D≤1。从图4 可以看出：损伤区域主要沿炮孔的径向扩展，与装药段平行的围岩中，随着深度增加，损伤区的影响半径变化不大，平均约2.41 m，体现出轴向耦合装药均匀爆轰的特点；在装药段的两端即炮孔的底部和堵塞段的底部，损伤区的影响半径较小，但在接近地表时，随着深度减小，损伤区的影响半径不断扩大，并在地表处达到最大值，约为3.93 m；在炮孔底部，随深度增加，损伤区的影响半径不断减小，并在孔底下方2.12 m处减小为0 m，此处即为损伤区影响的最大深度，约为6.62 m。

图4 基于本文提出模型的数值计算损伤分布云图Fig.4 Numerical calculation of damage distribution nephogram based on the proposed model in this paper

分析图4可知：炸药自孔底起爆以后，爆轰波以半球面波的形式猛烈地撞击药卷周围的空气，并在交界面处向空气中透射，形成空气冲击波；空气冲击波在炮孔内的空气层中传播时，随传播距离增加呈指数衰减[30]，直至传播至孔壁时，向孔壁岩石中透射，形成在岩石中传播的冲击波；由于岩石的波阻抗很大，该冲击波很快衰减为应力波，应力波继续在岩石中以指数形式衰减传播；冲击波和应力波在岩石中传播时，波阵面上的压力很大，且环向表现为拉应力，径向表现为压应力；冲击波和应力波的波阵面传播过后，岩石即出现初次损伤；在与装药段平行的围岩中，沿炮孔径向主要发生拉伸损伤，压缩损伤范围较小，集中在孔壁附近且远小于拉伸损伤范围内；伴随着应力波传播衰减，其波阵面上的压力、波速和质点移动速度不断降低，在炮孔径向上对岩石造成的损伤不断减小，直至损伤消失，在较远区域内只产生对岩石的扰动；当应力波传播到地表时，由于岩石的波阻抗远大于空气的波阻抗，应力波在地表与空气的交界面处反射，产生向岩体内传播的拉伸波；拉伸波传播之后，即对岩石造成二次拉伸损伤。由于拉伸波携带的能量在爆破总能量中占比较小，且衰减很快，因而其影响的范围有限，主要集中在地表面附近，导致自由面附近岩体在一定深度上损伤半径增大。在炮孔的底部和堵塞段的底部，药卷直接接触岩石，爆轰波直接透射入岩石，对炮孔底部和堵塞段底部岩石造成冲击压缩损伤，但压缩损伤的损伤半径较小，轴向影响范围有限。

2.3.2 与其他模型及实测结果的对比分析

由式(47)得出当初始损伤D0为0.4 时的爆破损伤阀值Df为0.57。将本文建立的拉压损伤模型、文献[9]所提出的模型以及TCK 模型分别导入三维模型中，计算损伤阀值Df为0.57 时的爆破损伤影响范围，得出：在与装药段平行的围岩中，由3种爆破损伤模型数值计算得到的爆破损伤影响范围相差不大，与实测范围都基本吻合；在与堵塞段平行的围岩中，基于本文所提出模型的计算范围与实测范围最接近，TCK 模型次之，文献[9]所提出的模型吻合度最低；在炮孔底部，文献[9]所提模型与本文所提模型数值计算结果相差较小，TCK 模型的计算范围比两者都小且与现场实测范围吻合度最差。

以孔口中心为原点，定义损伤影响的最大半径为Rx，最大深度为Ry，基于不同模型进行数值计算得到的损伤影响的最大半径和最大深度分别见表4和表5。

从表4和表5可以看出：由本文建立的拉压损伤模型、文献[9]所提出的模型和TCK 模型进行数值计算得到的最大损伤影响半径Rm分别为3.48，2.80和2.56 m，相较于实测值3.20 m的误差分别为0.28，0.40和0.64 m；最大损伤影响深度Hm分别为6.44，6.32 和5.80 m，相较于实测值6.20 m的误差分别为0.24，0.12和0.40 m。基于本文所提出的损伤模型进行数值计算得到的最大损伤影响半径与实测值最接近，且最大损伤影响深度与实测值的误差也比较小，总体上看，本文所提出的模型数值计算结果要优于文献[9]所提模型和TCK 模型的数值计算结果，其原因是后两者均忽视了压缩损伤，因而使装药段两端计算的损伤影响范围较小。

表4 最大损伤影响半径RmTable 4 The maximum damage radius Rm

表5 最大损伤影响深度HmTable 5 The maximum damage influence depth Hm

3 结论

1)本文所提出的爆破损伤模型包含了岩石的拉伸损伤和压缩损伤，可以反映岩石材料拉、压损伤不同的特性。模型中拉伸损伤变量被定义为给定裂纹密度下的断裂概率，压缩损伤变量被定义为等效塑性应变的指数函数，并由应变余能等效假说分别建立了压缩损伤和拉伸损伤造成的岩石刚度劣化的表达式。

2)通过分析岩石的单轴拉伸试验，阐明了拉伸损伤模型中定义裂纹密度函数的3 个材料常数(α，β和θc)的物理意义，并给出了3 个常数的取值方法。相比于其他模型，本文所提出的模型参数较少且物理意义明确，应用较方便。

3)本文所提出的拉、压损伤模型考虑了初始损伤的影响，且初始损伤可由工程现场声波测试得出，克服了现有模型较少考虑初始损伤的不足。

4)与其他模型相比，本文所提出的模型爆破损伤范围数值计算结果与现场实测结果最接近，证明了本文所提出的模型的合理性，适用于实际爆破分析。

5)在本文模型的构建过程中，将岩石材料简化为各向同性的理想弹塑性材料，存在一定局限性。岩石在爆破载荷下的损伤演化过程较复杂，需要开展更深入的研究工作方能对其进行更完整且合理描述。现有模型在很多方面尚需不断地修改与完善，以满足工程实际需要。