强风作用下树木周围流场的数值模拟研究

李正农，余世斌，吴红华，周利芬

(湖南大学建筑安全与节能教育部重点试验室，湖南长沙，410082)

我国是风灾频发的国家之一，不论是沿海地区的台风还是西北内陆地区的强风都可能对森林生态系统造成灾害性影响，也会带来巨大的经济损失。在强风作用下，树木可能会发生树枝折断甚至整体倒伏；树木也会对风速产生遮蔽和削弱效应，改变树木周围流场，如降低树后风速、增加树后湍流度等。研究树木对风场的影响对于改善近地面风环境，减轻强风对行人、建筑物或邻近树木的破坏等都具有十分重要的意义。目前，对于树木周围流场的研究，国内外学者主要采用现场实测、风洞实验及数值模拟3种方法。在现场实测与风洞实验方面，GUAN 等[1]通过风洞实验，得出了气动孔隙率、光学孔隙率以及树木阻力系数之间的关系。CAO等[2]对不同风速下3种乔木的阻力与倾覆力矩进行了研究，并同时分析了树木孔隙率、树木迎风面积、树顶位移、挠度、湍流度与风速之间的关系。MANICKATHAN 等[3]通过对比风洞实验中的人造模型树与小型天然树木之间的流场以及阻力系数的差异，发现只有当模型树和天然树具有相似的孔隙率，且模型树与天然树在风速不同情况下具备相同的空气动力特性时，模型树和天然树的阻力系数才具有相似性。

在数值模拟方面，SVENSSON等[4]将树冠简化为高为2.5 m、阻力系数为0.3、叶面积密度为2.1 m−1的长方形来研究二维树冠内外的流场分布；2004—2010 年，OHASHI 等[5−7]借用附加源项法的模拟方法，将树冠模型简化为简单的几何体并等效为多孔介质，最后以风速为指标深入分析了二维树木周围的流场。ROSENFELD 等[8]通过数值模拟并将柏树模型简化为三维圆锥形，以两排(每排3 颗树)组成三维防风林研究了树木之间的流场干扰作用。徐志[9]通过修正REALIZABLEk-ε模型算法，将树冠简化为高为5.8 m、宽为2.0 m的长方形，通过改变树冠层疏透性、树冠层高度、树冠层形状分析相应位置风场的变化规律。

以往的树木周围流场的数值模拟研究结果大多未与实测或风洞实验结果进行详细对比分析，且由于模拟技术的局限性对树木模型进行了一定简化，例如简化为长方体、圆锥体、棱台等。本文根据本课题组所完成的树木风洞实验，严格依据风洞试验时的树木模型外轮廓建立数值模拟模型。另外，以往对树木进行数值模拟时，孔隙率不变，而风洞实验结果表明，树木随着风速的增加，其孔隙率有所增大，阻力系数有所减小。此外，许多学者对树后流场进行分析时多只以风速为评价指标，对流场的湍流度分析较少。为此，在不同风速下，本文作者采用附加源项法改变阻力系数，研究孔隙率变化对树木的影响，并对树木周围湍流度进行分析，以便为理解树木在强风作用下的破坏机理提供支持，并对树木的种植及防护提供参考。

1 多孔介质的数值模拟

为了研究多孔介质的流动控制机理并进行力学分析，需要对多孔介质模型进行简化，建立合理的计算模型。现阶段对于多孔介质的模拟研究方法主要有2种：直接模拟法和附加源项法。直接模拟法是直接按照多孔介质对树木模型进行一定数量的开孔，再对其进行网格划分，这种方法因模型过于复杂较难实现，开孔区域模型的复杂性导致网格在该区域易发生畸变，从而影响数值计算效率与精度。附加源项法是基于实验测得气流流经多孔介质区域后速度、湍流度等一系列物理参数的变化情况，通过编译UDF(user define function)的形式，对多孔介质流域的动量、湍动能以及湍动能耗散率方程进行修正，通过在动量守恒方程、湍动能和湍动能耗散率方程中添加附加源项，对气流流经树木后的流动状况进行模拟。

对于厚度不是很大的多孔介质如很薄的挡风板，气流流过该区域后一般不会发生很复杂的流动，因而只对其动量方程添加附加源项即可。动量方程修正后的表达方式如下：

式中：Si为量方程的附加源项，定义为气流流经多孔介质域损失量；Dij为阻力系数矩阵；Cij为阻力系数矩阵；μ为气流的黏性系数；vi为气流在i方向上的速度；ρ为气流的密度，取1.225 kg/m³。

由于实际上气流雷诺数偏大，相较于其惯性阻力系数，其黏性阻力系数可以忽略不计。同时，为了简化计算，只需考虑气流在流动方向上的速度，Si简化为

式中：Cf为单位长度的阻力系数；Cd为树冠层阻力系数；η为树冠层叶面积指数(一般树种取2～4 m−1)，即单位土地面积上植物叶片总面积占土地面积的倍数[9]；D为多孔介质区域厚度，m；F为树冠层所受的阻力，N；Uref为参考风速，m/s；A为树木静止时迎风面的投影面积，m2。

树冠对湍流的影响由标准的k-ε模型修改。修改的基础是在树冠层内部的湍动能方程和湍动能耗散率方程中加入源项，可进行如下表达：

式中：μτ为湍流黏性系数；Gk为平均速度梯度引起的湍动能；常数C1ε=1.44，C2ε=1.92；σk为湍动能的湍流普朗特数；Sk为湍动能附加源项表达式；Sε为湍动能耗散率附加源项表达式。对于模拟近地面气流流经树木后的湍动能和湍动能耗散率附加源项模型Sk和Sε，国外学者进行了相关研究，国内对这方面的研究较少。数值模型大概可分为4种类型，见表1。

根据MOCHIDA等[10]简化的树木模型，并在前人研究的基础上，发现上述模型的第4 组(见表1)更能有效地模拟树木对湍流的影响，可将Sk和Sε分别表示为：

表1 湍动能和湍动能耗散率附加源项Table 1 Additional source terms for turbulent kinetic energy and turbulent kinetic energy dissipation rate

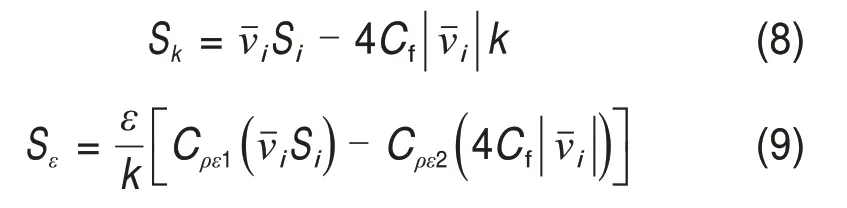
式中：Cρε1和Cρε2为附加源项系数，用于控制多孔介质中能量耗散过程的时间尺度。根据MOCHIDA等[10]算例中附加源项法各项系数的取值，建议将Cρε1和Cρε2分别取为1.8和1.5。

2 计算模型与数值方法

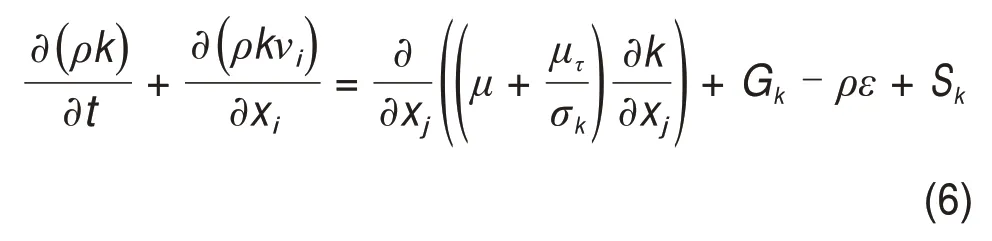
2.1 计算模型与网格划分

本文在计算时，树木模型取自风洞试验所用的豆瓣黄杨幼苗，该树木具有与实际树木相似的树冠形态、分支结构的材料构成，且树干与树枝、树枝与树叶之间的连接构造与真实树木的相同，因而，可以较好地模拟树木在风场中的反映。具体树木模型见图1。

图1 风洞实验树木模型Fig.1 Wind tunnel experiments with tree models

本文的树木模型高度H为50.0 cm，树干高度为10.0 cm，树冠最大厚度为25.4 cm，各截面半径见表2。

表2 树木各截面半径Table 2 Radius of each section of tree

该树木由于近似呈现中心对称图形，因此，在SolidWorks 利用相关点坐标，将1/2 纵截面通过旋转360°形成3D模型，见图2。

图2 数值风洞树木模型Fig.2 Model of numerical wind tunnel tree

计算域长×宽×高为750 cm×500 cm×250 cm，阻塞率为0.7%(<3%)，采用Icem 软件生成树木整体网格。由于树木形状不规则，因此，采用内外两部分，内部带有树木的网格采用非结构网格，其区域长×宽×高为20 cm×20 cm×60 cm；外部网格采用结构网格；总网格数目为202.7万个。具体网格分布见图3。

图3 网格分布Fig.3 Distribution of mesh

2.2 边界条件

计算域及边界条件见图4。计算域左边界设置成入口(inlet)，右边设置成自由出口(outflow)，外网格四周设置为无滑移的静止壁面(wall)，内外网格交界面设置为两流域交界面(interface)，树冠设置为内部面(interior)。

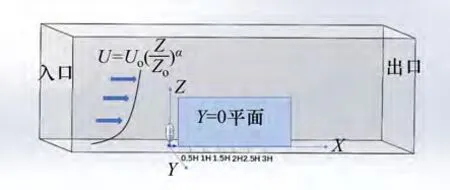
图4 计算域及边界条件Fig.4 Computational domain and boundary conditions

入口与风洞实验一致的B类地貌下的风场，其粗糙度系数α=0.15，缩尺比为1∶40，风剖面采用指数率分布，具体风剖面公式以及湍动能、湍动能耗散率公式见式(10)，(11)和(12)。风场的平均风速剖面和湍流度剖面见图5和图6。从图5和图6可以看出：模拟风场与实际风场较吻合，并且模拟湍流度与实际湍流度也较匹配，这在一定程度上验证了风场的稳定性。

图5 左边界速度进口模拟风速与实测风速对比Fig.5 Comparison of simulated wind speed and measured wind speed at the inlet of left boundary speed

图6 左边界速度进口模拟湍流度与实测湍流度对比Fig.6 Comparison of simulated turbulivity and measured turbulivity at the inlet of left boundary speed

式中：z为高度；z0为标准参考高度；U0为标准参考高度下的平均风速；U为该高度处的平均风速；k为湍动能；Iu为湍流强度；Cμ为常数；ε为湍动能耗散率；l为湍流积分尺度。

根据何定颖[11]的实验，分别以控制风速8，10，12和14 m/s，表示不同风速下的B类风场。具体控制风速对应实际离地高度10 m 处(风洞25cm高度处)的风速见表3。

表3 控制风速Ucon与树冠风速U10对应关系Table 3 Control wind speed and corresponding canopy wind speed

2.3 网格无关性的验证

现有模型的所有要素如冠层的多孔模型、湍流模型(包括修正的源项)和计算模型的范围都在以往的研究中得到了检验和验证[12−14]，特别是Fluent CFD 软件包的准确性和适用性得到广泛测试。由于本研究中使用的几何形状为树木的外轮廓，为了验证模型网格，本文对网格的独立性进行研究。

为了对比网格数目对计算结果的影响，采用202.7 万、411.5 万和963.1 万个网格(见图7)进行计算。网格总数调整通过改变整体网格数目实现。

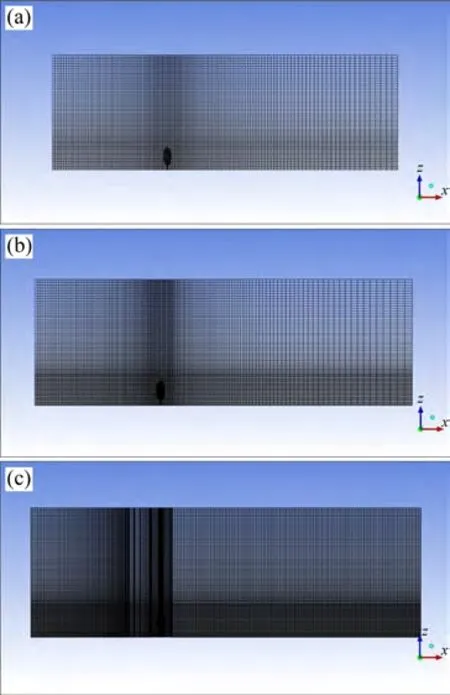
图7 顺风向网格布置Fig.7 Distribution of chord mesh

由实测风洞实验控制风速为10 m/s，阻力系数Cd为0.794，利用式(4)求得单位长度的阻力系数Cf为10.8，利用UDF导入Fluent中得到不同网格在高度1/2H处的轴向速度分布，见图8。

由图8可知：为了使数据变化更明显，以高度0.25 m(即1/2H)处沿顺风向取点，该点处于树冠影响最大的位置。虽然网格呈倍数增大，但对应求得的数值解并没有较大差别，最大相对误差为0.8%，说明模拟结果对网格数量的灵敏度较低，数值解较准确。

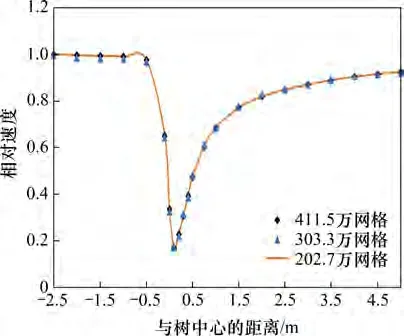
图8 不同网格在高度1/2H轴向速度分布Fig.8 Axial velocity profiles of different grids at height of 1/2H

2.4 流场计算方法

采用Fluent作为计算工具，求解流动控制方程获得树木流场的数值解。

通过稳态计算求解平均风速时，湍流模型选用具有比标准的k-ε模型精度高和稳定性强的RNGk-ε模型，并使用标准壁面函数(standard wall functions)对近壁面进行处理。流体材料选用理想不可压缩气体，材料参数使用默认值。采用SIMPLEC 方法对速度压力方程组进行解耦，SIMPLIC算法与SIMPLE算法相比，计算的收敛速度加快。离散格式使用二阶迎风格式(second order upwind)。稳态模拟计算的收敛标准为各项残差下降至10−4以下。

通过瞬态计算求解脉动风速，湍流模型采用可精确求解湍流尺度的大涡模拟(LES)。在稳态计算收敛后，以稳态计算结果作为初始流场，从而加快大涡模拟的收敛速度。进行大涡模拟计算时，使用WALE 模型，时间步长设置为Δt=0.005 s，时间步数为4 000步，子步迭代数为20。

冬季和冻融期生物过程对N2O排放具有重要影响的报道最早出现在1998年[36]。在寒冷冬季，深层土壤仍存在微生物活动，且积雪覆盖维持了雪下土壤相对温暖和稳定的环境，导致冬季土壤呼吸及CO2的持续排放[20，37]。Fahnestock et al.发现亚北极苔原在非生长季有土壤CO2排放[38]，并由此可以估算出亚北极苔原冬季CO2总排放量在全年占一定地位。更进一步分析，如果将这些地区冬季温室气体的排放量纳入其全年的C收支，将使亚苔原生态系统、高纬度地区生态系统的年C通量有不同程度的增加，甚至使其由温室气体的“汇”转变为“源”[39，40]。

3 计算结果与分析

3.1 10 m/s 控制风速下树后风剖面的模拟结果与实验结果对比

首先根据模型的树冠参数，将树冠直径10～50 cm按照所取坐标点分成10部分，利用面积法求解树冠的平均厚度；根据实验结果，利用式(4)得知10 m/s 控制风速下黄杨树苗的试验参数，见表4。

表4 黄杨数值模拟的参数Table 4 Numerical parameters of Boxwood

利用上述附加源项法将多孔介质相关系数添加入Fluent 的UDF 中。为了更好地分析模拟结果与实验结果的拟合程度，将树后不同距离的剖面与实验结果进行对比，见图9和图10。

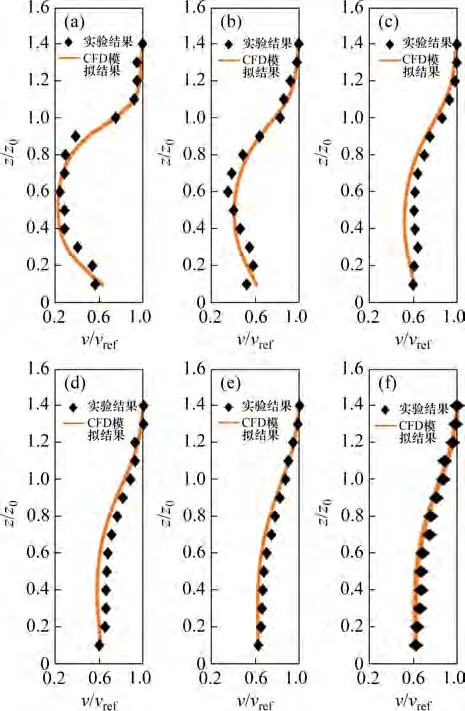
图9 树后不同距离剖面相对参考点风速νi/νref模拟结果与实验结果对比Fig.9 Simulation and experimental comparison of relative reference point wind speed in different distance profiles behind trees

为了方便比较，将模拟结果进行归一化处理，即将各测点的平均风速除以参考点处的平均风速，各测点的湍流度除以参考点处的湍流度，即

其中：vi为测点i处的平均风速；vref为参考点高度处的平均风速；Ii为测点i处的湍流度；Iref为参考点高度处的湍流度；σ为顺风向脉动风速均方根；uˉ为顺风向平均风速。

根据图像观察，0.2H～H是树后风场降低幅度最大的区间，这也是树冠所在的区间，与实验结果一致，说明实验与模拟的树后整体趋势一致。模拟中相对参考点风速最小值在最靠近树木的X=0.6H处的树冠中心位置，其值为0.223，而实验中相对参考点风速最小值为0.245，同样在树冠中心的位置，说明模拟结果与实测结果在数值上差别不大，而且在2H处，树后风速恢复了60%，这与实验结果相符。

从图9 和图10 可知，0.2H～H是树后湍流度影响幅度最大的区间，这也是树冠所在的区间，与实验结果一致，说明实验与模拟的树后风场整体趋势一致。模拟中相对参考点湍流度最大值在最靠近树木的X=0.6H处的树冠中心位置，其值为1.76，而实验中相对参考点湍流度最大值为1.65，同样在树冠中心位置，说明模拟结果与实测结果差别不大，而且在2H处，树后湍流度恢复到树前湍流度的80%，这与实验结果相符。

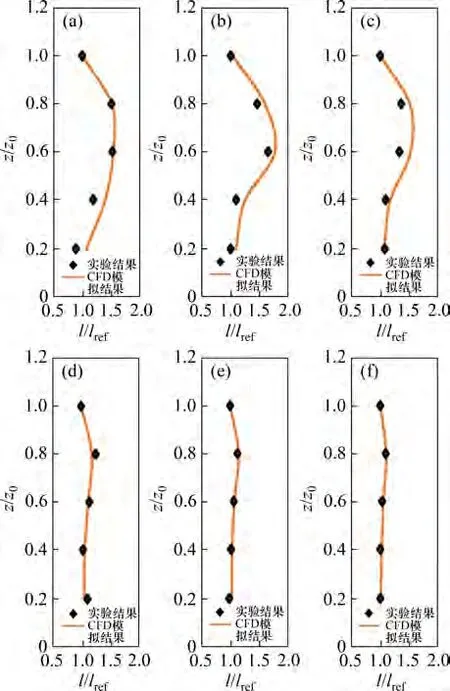
图10 树后不同距离剖面相对参考点湍流度Ii/Iref模拟结果与实验结果对比Fig.10 Simulation and experimental comparison of turbulence degree relative to reference point in different distance profiles behind trees

3.2 10 m/s控制风速下树后特定平面流场分析

为便于分析，以下结果均采用相对风速和相对湍流度进行分析，即将各测点处的平均风速和湍流度值除以无树时流场中相对应高度处平均风速νrel和湍流度Irel，计算公式如下：

其中：vi为测点i处平均风速；v0i为无树时流场中测点i处的平均风速；Ii为测点i处湍流度；I0i为无树时流场中测点i处湍流度。

3.2.1 横风向平面相对风速和相对湍流度分析

X=H时单棵树相对风速等值线见图11。从图11 可见：在X=H的横风向平面内，树木的相对速度以树冠中心(Y/D=0，Z/H=0.6)呈放射状向四周逐次增大，在树冠中心达到最小值0.5，数值结果与风洞实验结果一致；在水平方向上，当−0.5DH(树高)时，相对速度也大于0.9，因而可以忽略树木对于风速的影响；当Z<0.2H时，由于树叶在树冠位置，而在0.2H之下能影响流场的只有树干，因而，相比于0.2H～H处稠密度大、叶面积密度大的树冠区域影响要小得多。以上结果与风洞试验结果相符。

图11 X=H时单棵树相对风速等值线图Fig.11 Relative wind speed contour map of a single tree when X=H

用相对来流风速减少20%即相对风速为0.8所对应的距离d20描述树木的遮蔽效应[18]。Y/D=±0.5为树木的外轮廓范围，可发现d20的形状大致与树冠的轮廓线一致，但在靠近地面的区域，由于树干的宽度远小于树冠的宽度，对风速的减弱效果不明显，即树冠的形状决定了树木树后横风向平面的有效遮蔽范围，在风洞实验中也得出了类似结论。

X=H处单棵树相对湍流度等值线见图12。从图12 可以发现：在X=H的横风向平面内，树木的相对湍流度以树冠中心(Y/D=0，Z/H=0.6)呈放射状向四周逐渐减小，在树冠中心达到最大值2.49，且等值线的形状与树冠外轮廓线相似，这与风洞实验结果相一致；在水平方向上，当距离达到±0.75D时，相对湍流度达到1.42 且在这个范围之外，相对湍流度是逐渐接近于1；在高度方向，当Z>H(树高)时，向上则相对湍流度接近于1，可以认为在树高范围外树木对树后流场的影响可以忽略不计；当Z<0.2H时，向下则相对湍流度逐渐减小，在0.2H位置，由于其下仅有树干存在，对风场湍流度影响较小，相对湍流度接近于1.0，模拟中树木对湍流度的影响与风洞实验结果相一致。

图12 X=H时单棵树相对湍流度等值线图Fig.12 Relative turbulence contour map of a single tree when X=H

3.2.2 顺风面、水平面相对速度和湍流度分析

单棵树水平剖面风速云图见图13。由图13 可知：在水平剖面，风速减弱范围为椭圆形区域，越靠近树木，树木对风速的削弱作用越大，且在树冠中心相对风速达到最小值。结合图14，在垂直剖面中，3H处树后速度恢复树前速度80%，相当于树木的遮蔽区域d20在X=3H以内；此外，随着顺风向的距离增加，相邻两等值线之间的距离也逐渐增大，即在距离树木越远之处，降低同样的风速所需要的距离也越长；在高度方向上，可以明显地观察到在树冠高度以内，风速减弱效果明显，在树冠高度以外，相对风速接近于1，即对风速的影响较小。

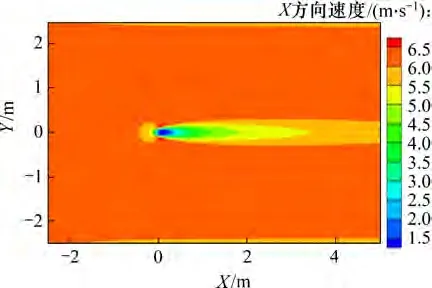
图13 单棵树水平剖面风速云图Fig.13 Nephogram of single tree horizontal profile wind speed

图14 树后Y=0平面相对风速等值线图Fig.14 Relative wind speed contour map behind tree in Y=0 plane

树后Y=0 平面相对湍流度等值线见图15。由图15 可知：在Y=0 的顺风向平面内，树木的相对湍流度以树冠中心呈半椭圆线向外逐渐减小，且在X=0.5H的树冠为中心处相对湍流度达到最大值2.67，越靠近树木，树木对湍流度的影响越大，在树冠中心相对湍流度达到最小值，这与风洞实验结果相同；在2H处，树后湍流度恢复树前湍流度的80%，且随着顺风向的距离增加，相邻两等值线之间的距离也逐渐增大，即距离树木越远，降低同样的湍流度所需要的距离越长；在高度方向上，可以明显地观察到在树冠高度以内，湍流度增强效果明显。

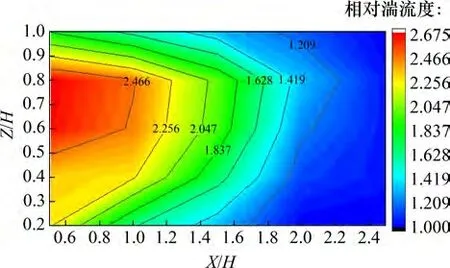
图15 树后Y=0平面相对湍流度等值线图Fig.15 Relative turbulence contour map in the plane Y=0 behind tree

3.3 不同控制风速下树后剖面分析

该风洞实验通过测量风速为8，10，12 和14 m/s时的流场，研究风速对树木形态的影响。利用何定颖等[12]实验结果，得到光学孔隙率β以及实验所测的阻力系数见表5，光学孔隙率β与单位长度的阻力系数Cf之间的关系见图16。

表5 实测光学孔隙率和阻力系数Table 5 Measured optical porosity and resistance coefficient

图16 光学孔隙率与阻力系数的关系Fig.16 Relationship between optical porosity and resistance coefficient

拟合的公式以及相关系数为

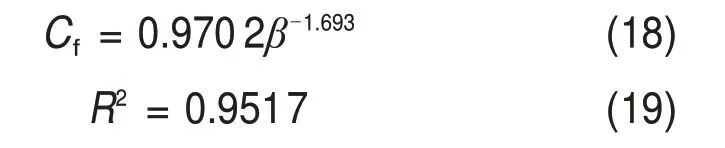
采用指幂指数的形式拟合光学孔隙率与阻力系数之间的关系，发现拟合的相关系数R2接近于1，说明拟合优度较高，再根据表2 以及图16，发现在同一树种下，随着风速增大，树木孔隙率逐渐增大，同时，阻力系数随着孔隙率增大而减小。

在不同控制风速下，利用不同阻力系数得到对应的相对参考点风速剖面以及相对参考点湍流度剖面，分别见图17和图18。

图17 不同风速下相对参考点风速剖面Fig.17 Relative reference point wind speed profile at different wind speeds

由图17 可知：在各个控制风速下，数值模拟和风洞实验得到的树后相对参考点风速剖面趋势基本一致，即在相对高度为(0～0.6)H时，随着高度增加，相对参考点风速呈减小趋势，在相对高度为(0.6～1.4)H时，随着高度增加，相对参考点风速呈增大趋势，并且在0.6H左右达到最小值。0.6H为树冠中心对应的高度，说明树冠中心对风速的减弱效果最明显；此外，在树冠高度范围内，随着控制风速增大，相对参考点风速剖面逐渐向右偏移，相对参考点风速最大值由8 m/s 时的0.39 增大到14 m/s时的0.47。这是因为随着风速增大，树冠较灵活的树叶和柔软的树枝受风速影响，沿着风向树叶和树枝进行了重新定向，树冠的变形会影响流经树木的气流流量以及由此产生的阻力系数。这种现象在成熟的树木现场测量中也有类似发现[15−17]。

不同风速下相对参考点湍流度剖面见图18。由图18 可知：在相对高度处于(0～0.6)H时，随着高度增加，相对参考点湍流度呈现增大趋势，在相对高度为(0.6～1.4)H时，随着高度增加，相对参考点湍流度呈减小趋势，并且在树冠中心处(0.6H)达到最大值；与风速分析结果相似，随着控制风速增大，树冠收缩变形，气流在通过树冠时受到树枝和树叶的扰动相对减弱，体现在树冠高度范围内相对参考点随着风速的增大而逐渐向左偏移。相对参考点湍流度的最大值由8 m/s 时的3.53 减小到14 m/s 时的2.79。同理，也是因为随着风速增加，树木树冠形状发生了改变，使得孔隙率增大，对湍流度的影响也逐渐减小。

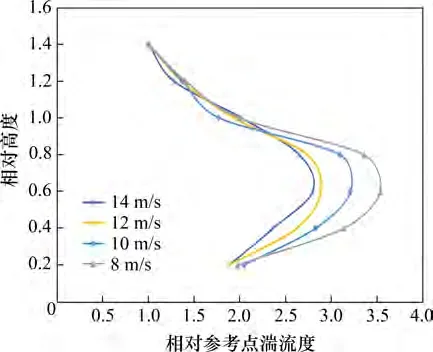
图18 不同风速下相对参考点湍流度剖面Fig.18 Relative reference point turbulence profile at different wind speeds

4 结论

1)利用Fluent可以有效模拟树木对风场的干扰效果，而且可以通过定量阻力系数模拟不同风速对树木周围风场的影响效果。

2)树木对树后流场的影响主要以树冠为中心，以椭圆形呈辐射状想四周扩展，距离树冠中心越远，树木对风速的削弱效果越小，对湍流度的影响也越小。在树后横风向平面(X=H)内，树木的遮蔽区域与树冠的区域相重合，与风洞试验结果一致。

3)对于同一种树木，随着风速增加，树木孔隙率逐渐增大，阻力系数相应减小；距离树木1倍树高处，风剖面的相对参考点风速最小值由0.39增大到0.47，相对参考点湍流度最大值由3.53减小至2.79；考虑因风速增大而导致树木阻力系数减小的情况，模拟的风场与风洞试验测量的风场仍然类似，说明附加源项法可以较好地模拟树后风场。