波形钢腹板部分斜拉桥施工阶段剪力滞效应分析

袁帅华，段文强，周聪，陈宁

(湖南科技大学土木工程学院，湖南湘潭，411201)

波形钢腹板部分斜拉桥是由波形钢腹板PC 组合箱梁桥与部分斜拉桥组合的新桥型[1−3]，目前人们对于这种新桥型剪力滞效应问题的研究尚少。国内外学者多研究波形钢腹板连续箱梁及普通混凝土箱梁的剪力滞问题，并在理论分析、有限元模拟、模型试验和工程实践中取得了一系列有价值的分析结果[4−20]，如：SA-NGUANMANASAK 等[9]通过建立不同网格尺寸及不同箱梁几何参数的有限元模型，对连续箱梁的剪力滞效应进行了计算分析，对剪力滞效应的影响因素进行了研究；GARA等[10]对求解剪力滞效应的有效宽度法进行了简化，对不同荷载作用下的双肋Π 型截面梁混凝土板中正应力分布情况进行了公式推导，并通过实桥对计算结果的准确性进行了验证；李立峰等[11−13]基于能量变分法、三杆比拟法对波形钢腹板PC组合箱梁桥的剪力滞效应计算公式进行了推导，并结合2根模型试验梁和有限元分析模型，对大跨径的波形钢腹板组合梁桥在施工阶段的剪力滞效应进行了系统研究；郭增伟等[14]针对传统比拟杆法分析等截面箱梁剪力滞效应的不足，重新推导变截面箱梁加劲杆等效面积及剪力滞效应微分方程，通过有机玻璃悬臂模型的试验结果检验了计算方程的正确性；陈千书等[15]建立了实体有限元分析模型，对某大翼缘宽箱梁矮塔斜拉桥施工阶段的剪力滞效应进行了计算分析，并通过对实桥应力监测，验证了理论分析的正确性；朱世峰等[16]建立了波形钢腹板PC组合箱梁桥的有限元分析模型，分析了不同箱梁承托长度、顶板厚度、悬翼比以及横隔板的设置对箱梁剪力滞效应的影响。随着波形钢腹板部分斜拉桥的建设数量逐渐增多，有必要对该种桥型的剪力滞效应特别是在施工阶段剪力滞效应的变化规律进行深入研究，以保障施工安全。本文以某单箱四室波形钢腹板部分斜拉桥为工程背景，通过数值方法与现场实测研究其在不同施工阶段剪力滞效应的分布规律。

1 工程背景

1.1 桥跨布置

以某跨径布置为(57.50+93.80+40.50)m，桥长为191.80 m的波形钢腹板部分斜拉桥为工程背景，其总体布置如图1 所示。主桥梁宽为24.50 m，主梁采用单箱四室波形钢腹板变截面箱梁，箱室宽度为5.60 m，悬臂长度为1.05 m，主梁跨中截面中心梁高为2.20 m，P11 中支点梁高为5.00 m，P12中支点梁高为4.40 m，边支点处梁高均为2.20 m。桥梁典型断面如图2所示。P11索塔总高度(包含与主梁结合部分)为24.95 m，其中，桥面以上塔柱高18.60 m；P12索塔总高度(包含与主梁结合部分)为21.70 m，其中桥面以上塔柱高为16.10 m。主梁、主塔采用C55 混凝土，波形钢腹板采用Q345qC钢，钢腹板厚度在14～22 mm 之间变化。图3 所示为波形钢腹板的节段示意和单位波长标准构造。

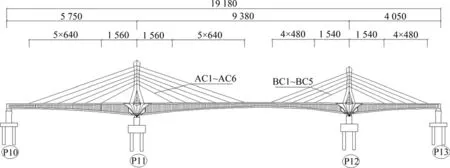
图1 主桥总体布置图Fig.1 General arrangement of main bridge

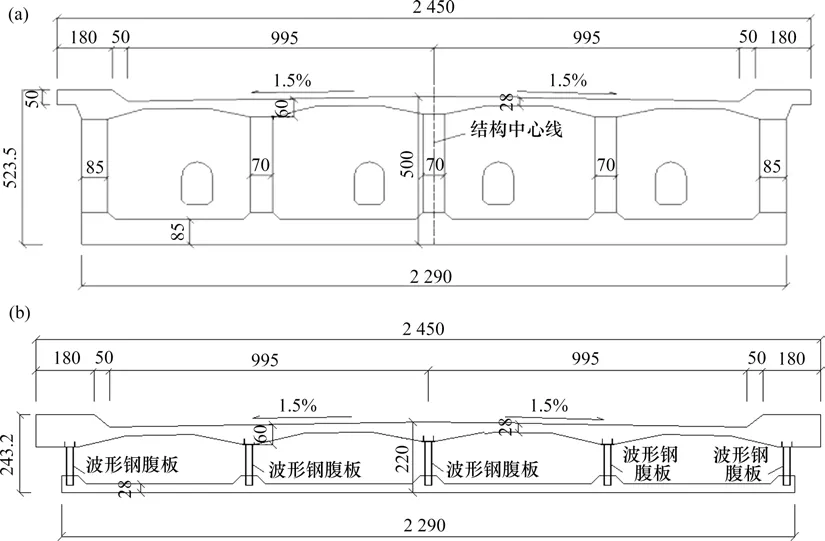
图2 典型截面示意图Fig.2 Typical cross sections

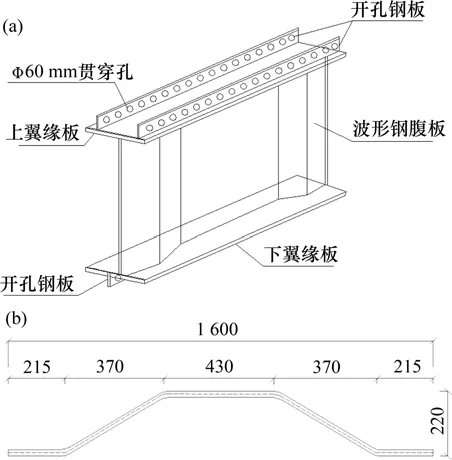
图3 波形钢腹板构造示意图Fig.3 Details of corrugated steel web

1.2 节段划分及控制截面的选取

a0 和b0 号节段采用支架现浇，悬臂现浇段采用挂篮施工[21]。主梁根据施工顺序共分为47 个节段，如图4 所示。选取a0 节段、a2 节段、a7 节段的端部断面作为有限元模型及现场应力监测的控制断面即图4中截面Ⅰ，Ⅱ和Ⅲ。

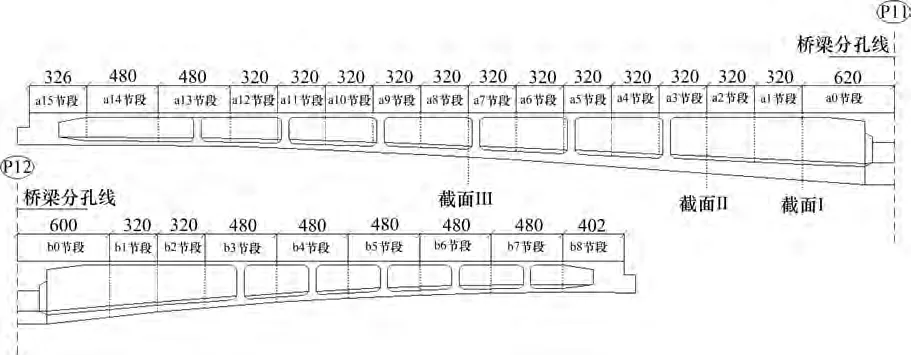
图4 施工节段划分示意图Fig.4 Arrangement of constructional segments

2 有限元模型的建立及验证

采用Midas Civil 对桥梁上部结构进行建模分析，其空间杆系有限元模型如图5所示。主梁、主塔采用梁单元模拟，斜拉索、预应力束采用桁架单元模拟，支座处采用一般支撑约束模拟，斜拉索与主梁、主塔连接采用刚性连接。全桥共划分为211个节点，182个单元，共建立48个施工阶段对全桥进行整体仿真分析。采用Midas FEA建立全桥1/2模型，混凝土顶、底板及横隔板采用实体单元，斜拉索采用桁架单元，波形钢腹板采用板单元，预应力钢束采用植入式钢筋模拟，见图6。

图5 空间杆系有限元模型Fig.5 Spatial frame finite element model

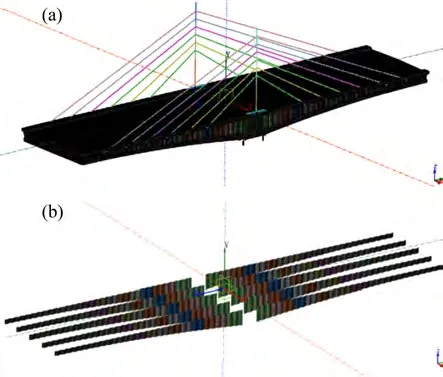
图6 空间实体有限元模型Fig.6 Spatial solid finite element model

为验证有限元模型的正确性，将最大悬臂阶段的有限元计算应力与现场实测应力进行对比，实测应力测点如图7 所示，对比结果见表1 和表2(其中，应力正值表示拉应力，负值表示压应力)。经对比可知，有限元应力与实测应力较吻合，两者最大z 相对误差为9.75%，表明有限元计算结果比较精确。

图7 主梁应变监测断面应变计布置图Fig.7 Gages arrangement of strain monitoring sections

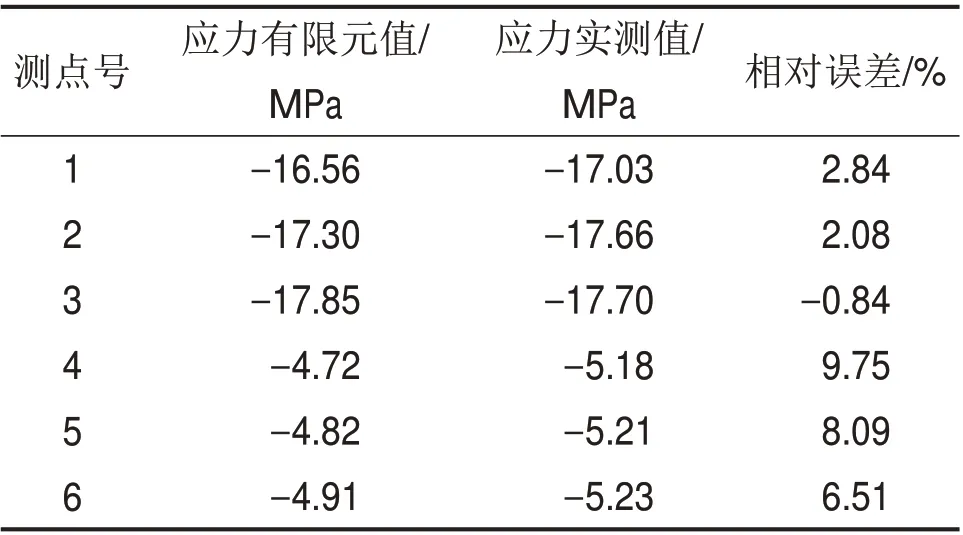
表1 截面Ⅰ应力有限元值与实测值对比结果Table 1 Stress comparison of numerical values and field values in section Ⅰ

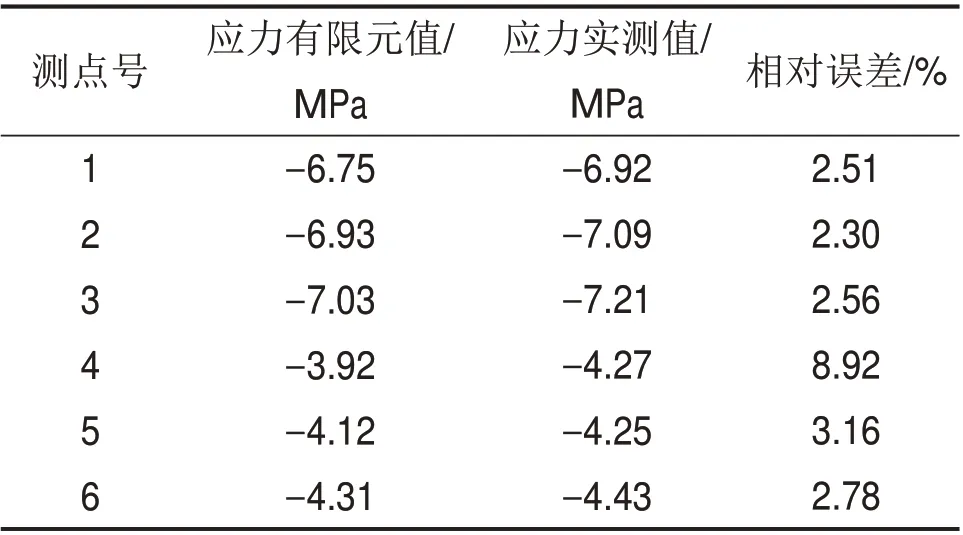
表2 截面Ⅲ应力有限元值与实测值对比结果Table 2 Stress comparison of numerical values and field values in section Ⅲ

3 最大悬臂阶段剪力滞效应分析

a14 和a14`节段预应力张拉后，桥梁处于最大悬臂状态，为整个悬臂施工过程中最不利状态。以箱梁横向为x方向，横截面中心点为坐标原点，控制截面的顶、底板纵向正应力分布情况如图8所示。

由图8可知：在最大悬臂状态下，控制截面Ⅰ，Ⅱ和Ⅲ的实体模型顶、底板纵向正应力沿梁宽方向不均匀分布，应力峰值位于腹板与顶、底板连接处位置；实体模型在连接处位置的纵向正应力比杆系模型的大，远离连接处位置的纵向正应力则逐渐减小，3个控制截面的顶、底板呈明显的正剪力滞效应。

用剪力滞系数λ表征剪力滞效应的变化规律[22]，与图8 相对应的剪力滞系数分布情况如图9所示。由图9 可知：最大剪力滞系数位于截面顶、底板横向中心点位置，3个控制截面顶板的最大剪力滞系数分别为1.32，1.21和1.09，底板截面的剪力滞系数峰值分别为1.11，1.10和1.08，顶板剪力滞系数明显比底板的大；截面顶板的剪力滞系数沿悬臂方向逐渐减小，而底板的剪力滞系数的变化幅度则不明显。

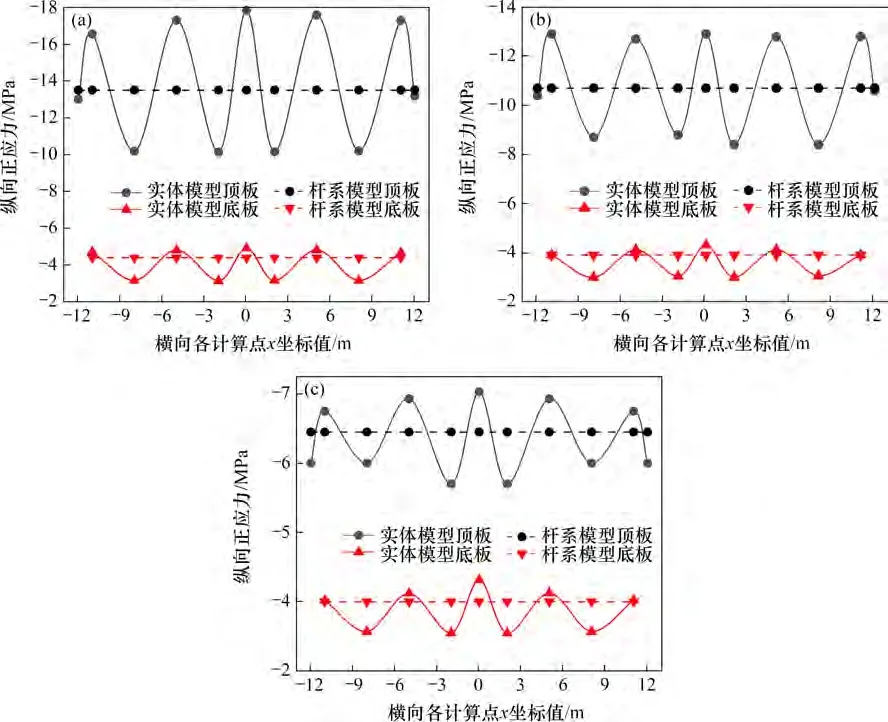
图8 控制截面顶、底板纵向正应力分布Fig.8 Distribution of normal stress on top and bottom flanges of control sections

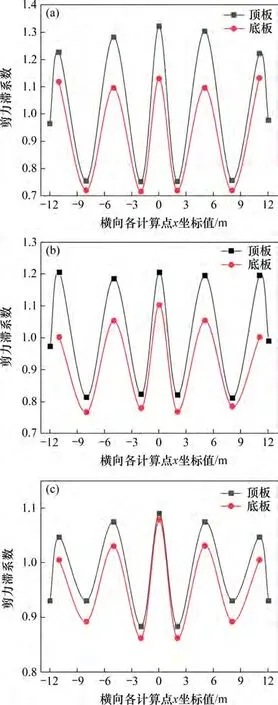
图9 最大悬臂状态时控制截面剪力滞系数Fig.9 Shear lag coefficient distribution of control sections at the maximum cantilever state

4 施工全过程剪力滞系数分析

图10所示为施工全过程中截面Ⅰ及截面Ⅲ腹板与顶板连接处3个应力测点的实测值与有限元值的对比结果。由图10可知：3个测点的应力实测值与有限元值总体变化趋势一致，实测值略大于有限元值；3号测点的应力最大，2号测点的应力次之，1号测点的应力最小。

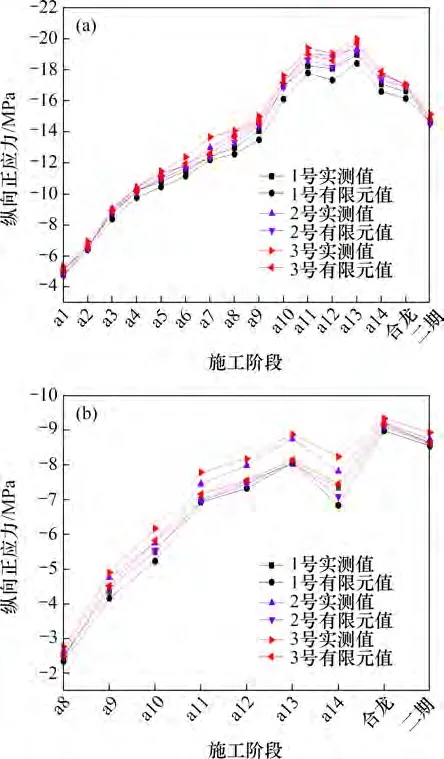
图10 截面I和Ⅲ顶板实测应力与有限元应力对比Fig.10 Stress comparison of field results and numerical values at top flanges of typical sections

图11所示为截面Ⅰ及截面Ⅲ腹板与顶板连接处3 个测点的剪力滞系数在施工全过程中的变化规律，实测剪力滞系数稍大于有限元剪力滞系数，但两者的总体变化趋势一致。

由图11(a)可知：悬臂施工节段由a1 节段向a9节段推进时，靠近主梁零号块的截面Ⅰ剪力滞系数呈增大趋势；在施工a10～a12节段时，剪力滞系数有所减小，但变化趋势不大；在a12节段施工完成后剪力滞系数继续增大，其主要原因是a12 和a14节段为无斜拉索张拉节段，a13～a14节段长度大于先前节段长度，节段自重更大，从而引起剪力系数继续增加；在a14 节段完成后即最大悬臂状态，剪力滞系数达到最大值，在全桥合龙后剪力滞系数呈下降趋势，且下降幅度比较明显。3个测点的最大剪力滞系数均出现在最大悬臂状态，3号测点的剪力滞系数变化趋势最明显。

由图11(b)可知：位于边跨L/2处的截面Ⅲ的剪力滞系数变化趋势与截面Ⅰ的剪力滞系数变化趋势有所不同，在悬臂施工阶段呈下降趋势，在全桥合龙后剪力滞系数变化趋于平缓，3个测点的最大剪力滞系数均出现在a8节段施工完成后。

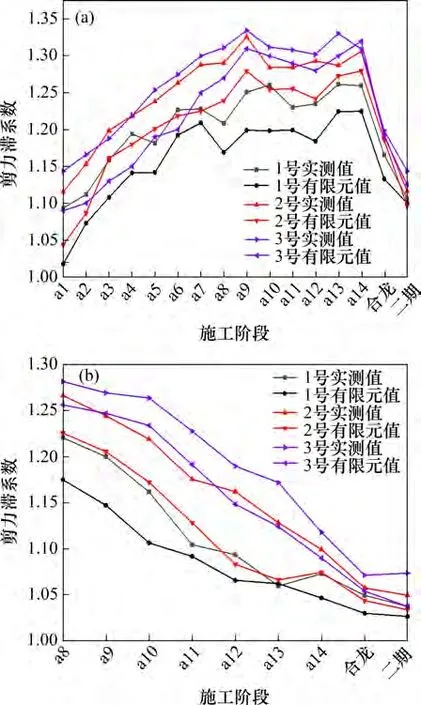
图11 施工全过程顶板剪力滞系数变化曲线Fig.11 Change curves of shear lag coefficients of top flanges during the whole construction

综合上述分析，波形钢腹板部分斜拉桥悬臂施工时，需对靠近主梁零号块的箱梁截面应力变化情况重点关注，特别是在悬臂施工后期，在施工无索区节段时，避免应力超限，影响结构安全。而对远离零号块的箱梁截面，则需关注随后施工节段对其应力变化的影响。

5 结论

1)悬臂施工过程中波形钢腹板部分斜拉桥主梁控制截面呈明显的正剪力滞效应，截面剪力滞系数峰值位于腹板与顶、底板连接处。控制截面的顶板剪力滞效应相比于底板更显著。

2)控制截面的剪力滞效应在悬臂阶段初期增长趋势较明显，全桥合龙后呈下降趋势。在施工全过程中，靠近零号块截面的顶、底板剪力滞系数最大，分别达1.32和1.19，因此，在波形钢腹板部分斜拉桥悬臂施工时，需对该截面的应力变化情况进行重点监测。