带分片光滑约束函数优化问题的区域分割方法

王柳婷， 刘庆怀， 商玉凤， 刘傲多

(1.长春工业大学 数学与统计学院， 吉林 长春 130012;2.长春财经学院经济学院， 吉林 长春 130122；3.长春建筑学院 基础教学部， 吉林 长春 130607)

0 引 言

许多实际问题中的优化问题常常是非凸优化问题，因此解决非凸优化问题的理论和算法始终是优化领域的热点问题。近年来，文献[1-5]给出了非凸优化问题在满足法锥条件、拟法锥条件或伪锥条件下的组合同伦方程。文献[6]提出动约束组合同伦方法。文献[7]给出了一类带洞非凸域上函数极值的动约束同伦算法。对于非凸非光滑优化问题学者们也提出了很多办法，如凝聚同伦方法[8-10]、迫近束方法[11]、拟牛顿型束方法[12]、近似凸差分解方法[13]、不可行迫近束方法[14]、邻近增量聚合梯度方法[15]、邻近滤子束方法[16]等。文献[17]针对单洞非凸优化问题首次提出区域分割方法，在原问题的约束函数为光滑函数的条件下，证明了子问题与原问题KKT解的关系。文中将区域分割方法应用于求解非凸非光滑优化问题，并且证明了子问题KKT解与原问题KKT解的关系。

1 预备知识

考虑非凸非光滑优化问题

(1)

其中,f:Rn→R，gi:Rn→R(i=1,2,…,m+1)，f,gi(i=1,2,…,m+1)是连续可微的，x∈Rn。令

该函数是分片光滑函数，从而问题(1)也称为带分片光滑约束函数的优化问题。

文中设

gm+1(x)=‖x‖2-r2，

其中,ai=(ai1,ai2,…,ain)T∈Rn，bi∈R，1≤i≤m，r∈R++，m>n(文中取m=n+1)。

记号如下：

Ω={x|h(x)≤0,gm+1(x)≤0}为可行域，Ω0={x|h(x)<0,gm+1(x)<0}为严格可行域，∂Ω=ΩΩ0为可行域边界，

D1={x|h(x)≥0}，

D2={x|gm+1(x)≤0}，

M={1,2,…,m}，

I(x)={i|gi(x)=0,i=1,2，…,m}，

b=(b1,b2,…,bm)T∈Rm。

假设条件1:

1)D1有界，即存在一个常数d，对任意x∈D1满足‖x‖≤d。

2)∂Ω是正则的，即∀x∈∂Ω，∇gi(x)(i∈I(x))正线性独立，若I(x)=∅，则∇gm+1(x)≠0。

对问题(1)中的约束函数作如下假设。

假设条件2:

1)令B=(A,b)，满足|B|≠0，其中A=(a1,a2,…,am)T。

2)A满足ai×aj≠0，其中i,j=1,2,…,m，且i≠j。

3)对∀x∈∂D1，有

gi(x)>0,i∈MI(x)。

(2)

在上面假设条件下可行域如图1所示(R2情形)。

图1 R2上的可行域

由于问题(1)中的约束函数h(x)是非光滑函数，所以在讨论最优性一阶必要条件时需要如下非光滑分析结论。

引理1[18]如果f:Rn→R在Ω上是局部Lipschitz连续的，且在x∈Ω处达到局部极小，则

0∈∂f(x)+NΩ(x)，

这里∂f(x)是f(x)在x处的Clarke广义梯度，NΩ(x)是Ω在x∈Ω处的法锥。

引理2[18]如果f(x)在x处是连续可微函数，则

∂f(x)={∇f(x)}。

推论1[18]若f(x)是连续可微的，且在Ω上于x∈Ω处达到局部极小，则

-∇f(x)∈NΩ(x)。

针对问题(1)，在满足假设条件1和假设条件2的条件下，对∀x∈∂Ω，在x处的法锥分为如下两种情况：

1)当I(x)≠∅时，则

2)当I(x)=∅时，则

NΩ(x)={ym+1∇gm+1(x)|ym+1≥0}。

若问题(1)在x∈∂Ω处达到局部极小时，由引理1和引理2可知，

-∇f(x)∈NΩ(x)。

即当I(x)≠∅时，存在yi≥0,i∈I(x)，使得

当I(x)=∅时，存在ym+1≥0，使得

∇f(x)+ym+1∇gm+1(x)=0。

综上，问题(1)在x∈∂Ω处达到局部极小时，一阶最优性必要条件(也称为KKT系统)可写成

(3)

或

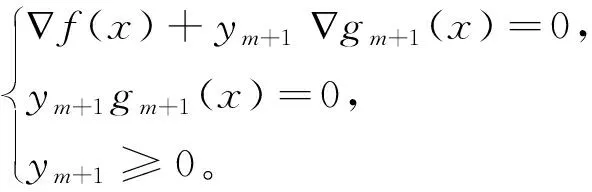
(4)

2 主要结论

引理3

2)若r>d成立，则Ω0非空。

令

证毕。

由于问题(1)是一类带洞非凸非光滑优化问题，因此根据文献[17]提出的区域分割方法，将可行域Ω用g1(x)=0分割成Ω1和Ω2两个区域，记

Ω1={x|g1(x)≥0,h1(x)≤0,gm+1(x)≤0}，

Ω2={x|g1(x)≤0,gm+1(x)≤0}，

从而问题(1)被分解为如下两个子问题。

(5)

s.t. minf(x),

g1(x)≤0,

gm+1(x)=‖x‖2-r2≤0。

(6)

I1(x)={i|gi(x)=0,i=1,2,…,m+1}，

I2(x)={i|gi(x)=0,i=1,m+1}，

I3(x)={i|gi(x)=0,i=2,…,m}。

引理4对∀x∈∂Ω1，有∇gi(x)(i∈I(x)),∇gm+1(x)正线性独立。

证明 由假设条件1和2可知，只需证明以下两种情况。

1)当I1(x)={1,m+1}时，{∇gi(x)|i∈I1(x)}正线性独立。

2)当1≤#I3(x)≤m-2时，∇g1(x)，∇gi(x)(i∈I3(x))正线性独立。

下面证明第一种情况。

由已知得

∇g1(x)=a1，

∇gm+1(x)=2x，

假设∇g1(x),∇gm+1(x)正线性相关，则存在λ∈R+，使得

a1+2λx=0,

那么

由于λ≠0，将上式代入g1(x)=0，gm+1(x)=0联立可得

即

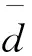
下面证明第二种情况。

由假设条件2中|B|≠0可知，

所以(a1,a2,…,am-1)构成一组基底，即向量组(a1,a2,…,am-1)线性无关，∇g1(x),…,∇gm-1(x)正线性独立。

那么当1≤#I3(x)≤m-2时，∇g1(x)，∇gi(x)(i∈I3(x))正线性独立。

证毕。

由引理1类似于问题(1)的KKT系统的讨论，得问题(5)的KKT系统为

(7)

引理5对∀x∈∂Ω2，有∇gi(x)(i∈I2(x))正线性独立。

证明 由引理4即可得到。

问题(6)的KKT系统为

(8)

令S={x*∈Ω|x*为问题(1)的KKT解}，S1={x*∈Ω1|x*为问题(5)的KKT解}，S2={x*∈Ω2|x*为问题(6)的KKT解}。为求解该非光滑非凸域上优化问题(1)的KKT解，给出以下定理。

定理1若x∈S1且g1(x)>0，则x∈S。

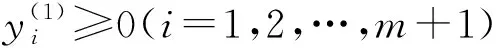
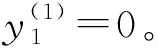
1)若m+1∈I1(x)，则式(9.1)可写为

2)若m+1∉I1(x)，则式(9.1)可写为

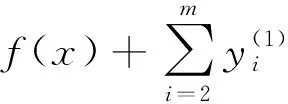
综上所述，若x∈S1且g1(x)>0，则x∈S。

证毕。

定理2若x∈S2，但x∉Ω1，则x∈S。

1)若m+1∈I1(x)，x∉Ω1，则式(10.1)可写为

2)若m+1∉I1(x)，x∉Ω1，则式(10.1)可写为

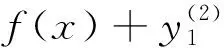
综上所述，若x∈S2，但x∉Ω1，则x∈S。

证毕。

定理3若S1∩S2≠∅且x∈S1∩S2，则x∈S。

分两种情况讨论:

1)若m+1∈I1(x)，由式(11.1)和式(12.1)相减得

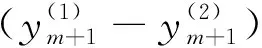
再由引理4和引理5可知，∂Ω1,∂Ω2是正则的,则

那么

又因为

所以

2)若m+1∉I1(x)，由式(11.1)和式(12.1)相减得

则同1)可得

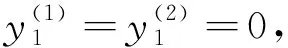
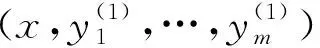
综上所述，若S1∩S2≠∅且x∈S1∩S2，则x∈S。

证毕。

为了证明下面定理，先给出引理6，且以下讨论的S、S1和S2分别是问题(1)、问题(5)和问题(6)是局部极小解。

引理6若x∈S，则x∈S1且x∈S2。

定理4设x∈S1，若x∈Ω2，x∉S2且g1(x)=0，则x∉S。

证明 假设x∈S，

根据引理6可得x∈S1且x∈S2。

与x∉S2矛盾，故x∉S。

证毕。

定理5设x∈S2，若x∈Ω1，x∉S1且g1(x)=0，则x∉S。

证明 假设x∈S，

根据引理6可得x∈S1且x∈S2。

与x∉S1矛盾，故x∉S。

证毕。

3 结 语

讨论的可行域为带分片线性约束的非凸可行域，针对上述区域，给出一种区域分割方法，并证明了在一定条件下可以通过求子问题的解得到原问题的解。区域分割方法能够解决更加复杂的非凸优化问题。将区域分割方法应用于实际问题和更多复杂的可行域是接下来的研究工作。