全球定位/惯性导航组合导航改进UKF算法

韩 博， 胡黄水， 曹学瑶， 王宏志

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

0 引 言

目前，单一的导航系统在应对不同的场景如市区或者大型商城，其可靠性大大降低，因此导航的方式也从单一导航演变到组合导航。GPS定位精度虽然高，但其信息不够全面，频带窄，易受干扰。而惯性导航系统(INS)虽然不受外界环境干扰，但其误差会随时间不断累计，长期精度差。GPS/INS的组合方式则互相弥补了对方缺点，是组合导航中最常用的组合方式[1-3]。

GPS/INS的组合方式分为松组合、紧组合以及深组合。松组合结构简单，因此操作起来不复杂，其GPS和INS可独立工作，组合方式表现在用GPS修正INS数据；紧组合中GPS和INS相互辅助，其基本模式是伪距及伪距率的组合，工程难以实施且计算量大；深组合又叫超紧组合，其将INS的测量值反馈给GPS，并通过GPS和INS组合滤波后的导航信息修正INS[4]。同样其结构复杂且计算量大。因此，文中采用松组合方式[5]。

由于标准的卡尔曼滤波(KF)不能处理非线性系统[6]，因此学者们在KF的基础上又提出了扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)、粒子滤波(PF)等。但相比之下，UKF因其精度高且计算量小的特点，被广泛应用在各个领域。但随着系统维数和非线性度的增加，其滤波效果也会变差[7]。系统中的不确定性干扰以及自身对误差模型较敏感，也会导致UKF的滤波精度产生影响[8]。

为了进一步提高组合导航精度，学者们提出一些与其他算法结合的方式，如文献[9]提出基于粒子群优化的UKF算法，文献[10]提出神经网络辅助的GPS/INS组合导航自适应UKF算法等。由于算法涉及训练及学习，虽然提高了滤波的精度，但大大增加了滤波的计算量。文献[11]提出基于GPS/INS的自适应无迹卡尔曼滤波算法，采用自适应窗口对系统噪声和测量噪声进行修正，同时改进次优渐消因子，使得状态预测协方差次优渐消因子不需要计算雅克比矩阵求取，最后引入统计量，从而确定模型不确定性检测阈值。该算法一定程度上提高了滤波精度和收敛性，但对于优渐消因子求取过程复杂，同时加窗的检测也一定程度上延长了滤波时间。文献[12]提出一种改进的无迹卡尔曼滤波在SINS/GPS组合导航中的应用，该算法加入了对观测量的判断，并引入抗差因子对异常的观测量进行修正，从而提高系统的滤波精度和鲁棒性，但其引入的多个参数都需要经验取值。文献[13]提出一种改进的UKF在GPS/INS组合导航中的应用，在传统UKF算法上引入最小偏度单形采样策略,降低了UKF计算量，但其Simga的权值则需要经验取值。同时引入自适应因子调整过程噪声，从而降低动态异常干扰误差对UKF精度与稳定性的影响,未考虑系统噪声Q以及测量噪声R。文献[14]提出一种基于UKF的INS/GPS组合导航系统仿真，通过引入自适应因子仅对系统噪声Q以及测量噪声R进行修正，一定程度上提高滤波精度和收敛速度。

针对以上问题，在UKF的基础上引入自适应因子，根据系统状态确认自适应因子的值，从而选择对系统参数进行修正，使得滤波系统具有自我调节能力。仿真实验表明，文中提出的改进UKF算法滤波效果优于UKF和文献[14]提出的UKF算法。

1 组合导航

GPS/INS松组合结构框图如图1所示。

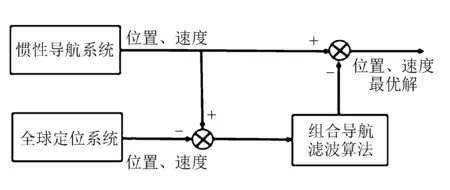
图1 GPS/INS松组合结构框图

将INS与GPS输出的速度及位置进行做差后，将做差的数据传输到组合导航滤波算法中作为输入量进行数据融合，经过滤波处理后得到的数据对INS输出的速度及位置进行修正[15]。

松组合状态方程：

Xk=Fk-1*Xk-1+Wk-1,

(1)

Xk-1=[σL，σλ，σh,σve，σvn，σvu,φe，φn，φu,

εbx，εby，εbz,∇ax，∇ay，∇az]，

式中：σL，σλ，σh----位置误差;

σve，σvn，σvu----速度误差;

φe,φn,φu----姿态角误差;

εbx，εby，εbz----陀螺仪常值漂移;

∇ax，∇ay，∇az----加速度计的零偏;

Fk-1----状态转移矩阵;

Wk-1----系统噪声[16]。

松组合测量方程

Zk=Hk*Xk+Vk,

(2)

式中：Hk----测量转移矩阵;

Vk----测量白噪声。

选取GPS与INS速度、位置差值为测量方程的观测值。

2 改进算法设计

2.1 UKF算法

1)选定滤波初值：

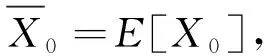
(3)

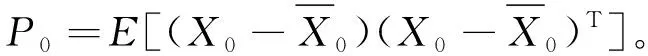
(4)

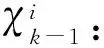
(5)

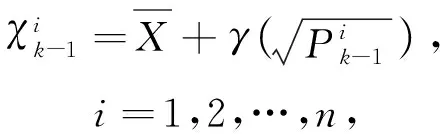
(6)

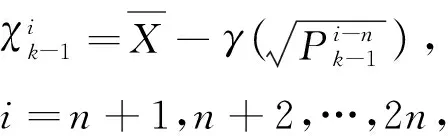
(7)

(8)

λ----比例因子,λ=α2(n+k)-n。

Sigma点的分布状态由α值决定，通常取0≤α≤1，文中取α为0.001。

3)确定Sigma点的权值大小：

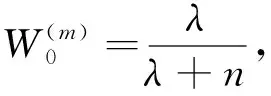
(9)

(10)

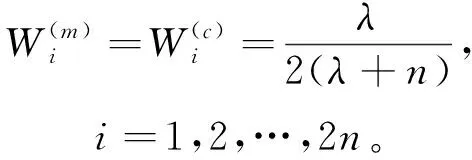
(11)

式(10)中的β为状态分布参数，β≥0，调节β值可以提高方差的精度，文中取β=2。

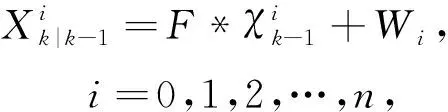
(12)

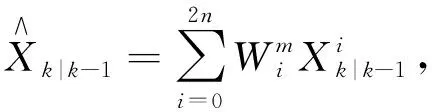
(13)

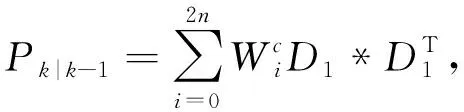
(14)

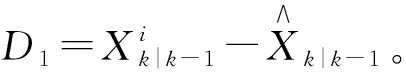
(15)

(16)

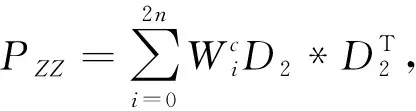
(17)

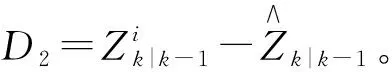
6)更新状态。计算状态预测与测量估计的协方差

(18)

计算滤波增益

(19)

状态和方差更新：

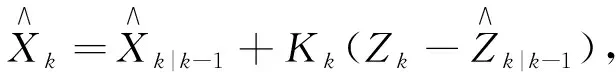
(20)

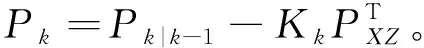
(21)

2.2 改进UKF算法(IUKF)

IUKF算法通过监测系统滤波是否处于正常状态，并自发地进行相应的调节，从而达到降低系统不确定性对滤波产生的影响。

1)修正滤波参数Pk|k-1，PZZ,PXZ。

求残差系数

ek=Zk-Zk|k-1。

(22)

求自适应因子

(23)

修正参数Pk|k-1，PZZ,PXZ：

(24)

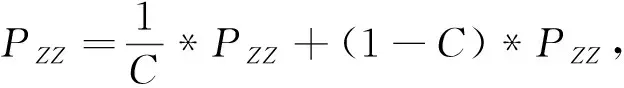
(25)

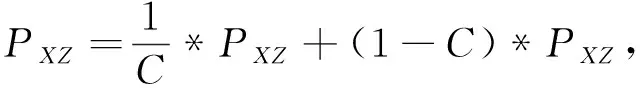
(26)

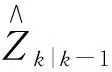
2)修正滤波参数系统噪声Q和测量噪声R。

求加权系数

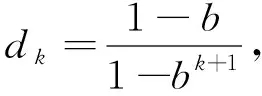
(27)

式中：b----遗忘因子，其取值一般为[0.95，0.99]，文中取0.95[17]。

修正参数Q,R:

Qk=C*((1-dk)Qk-1+

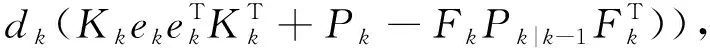
(28)

Rk=C*((1-dk)Rk-1+

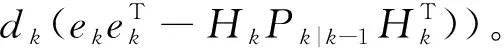
(29)

Q,R在系统中是实时变化的，同时由于理论与实际的噪声数值存在偏差，当系统的不确定性干扰影响正常滤波过程时，也会导致参数Q,R出现误差，若不进行修正，误差则会随时间不断累加。当C不为1时，则通过式(28)、式(29)修正Q,R，减小由于系统不确定性干扰导致Q,R偏大而导致滤波精度下降的问题；当C为1时，则正常对Q,R进行修正。

3 仿真测试

通过Matlab对文中提出的IUKF算法以及对比算法UKF、文献[14]提出的UKF算法进行仿真；仿真中将文献[14]提出的方法记为14-IUKF。

初始滤波参数见表1。

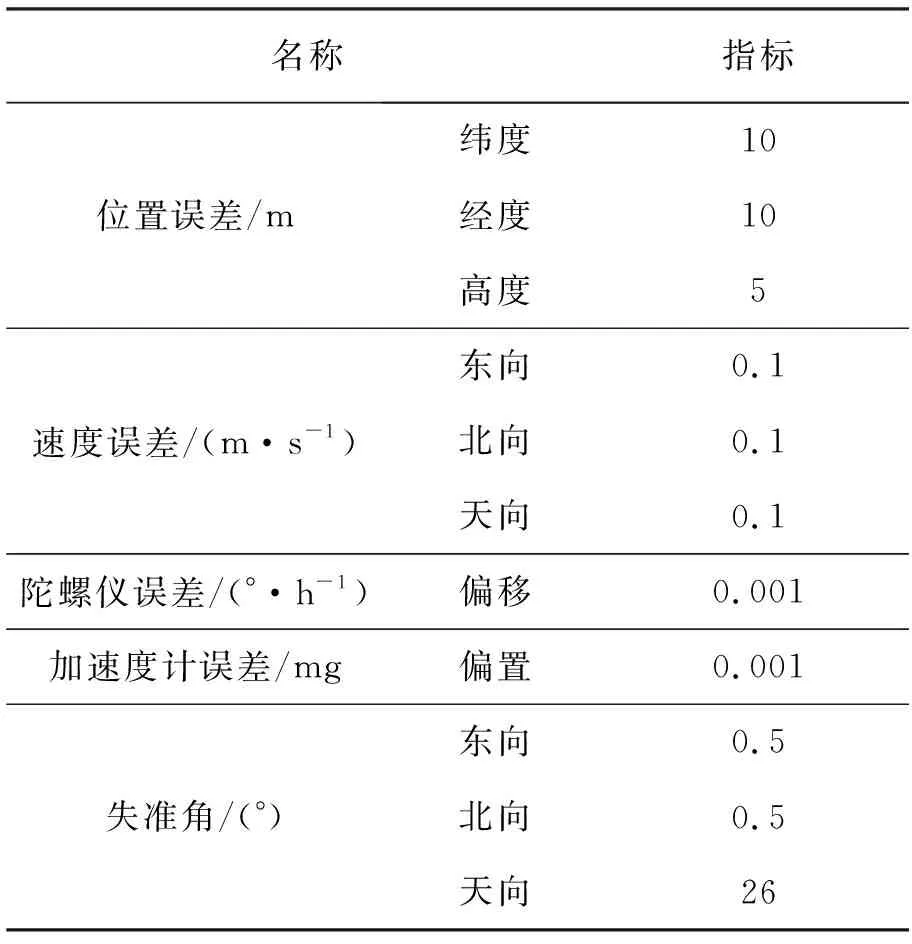
表1 滤波参数

仿真总时常为500 s,载体初始位置为东经125.39°，北纬44.01°，初始速度为0。

位置误差东-北-天方向的对比仿真和速度误差东-北-天方向的对比仿真分别如图2和图3所示。

从图2可以看出，在东向、天向，IUKF算法相比UKF及14-IUKF算法，其仿真曲线更加集中分布在虚线内，曲线波动幅度小于另外两种对比算法。在北向，IUKF算法与14-IUKF算法仿真曲线基本都集中分布在虚线内，但IUKF算法的波动幅度略小于14-IUKF算法。

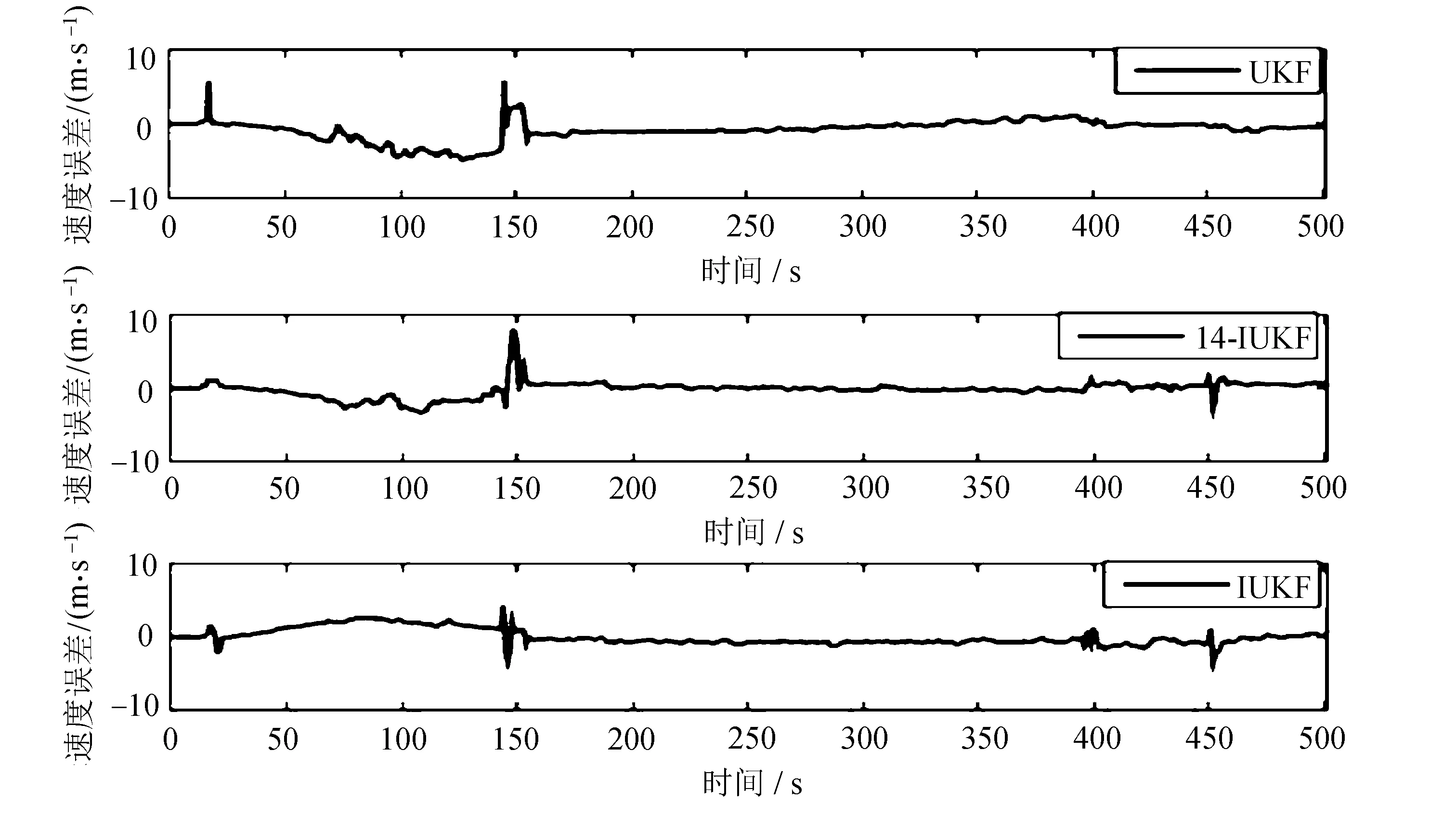
从图3同样可以看出，在速度误差的三个方向对比中，IUKF算法曲线波动范围均小于对比算法14-IUKF和UKF。

最大误差对比和最小误差对比分别见表2和表3。

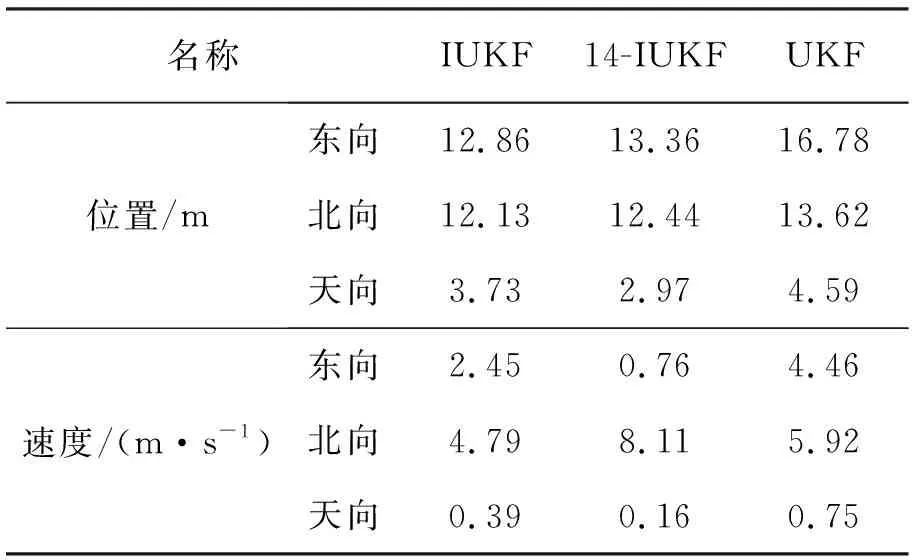
表2 最大误差对比

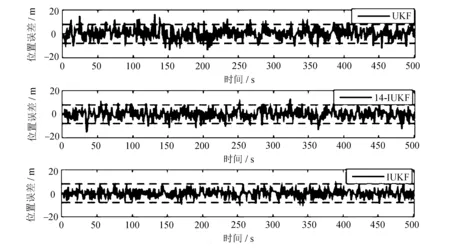
(a) 东向

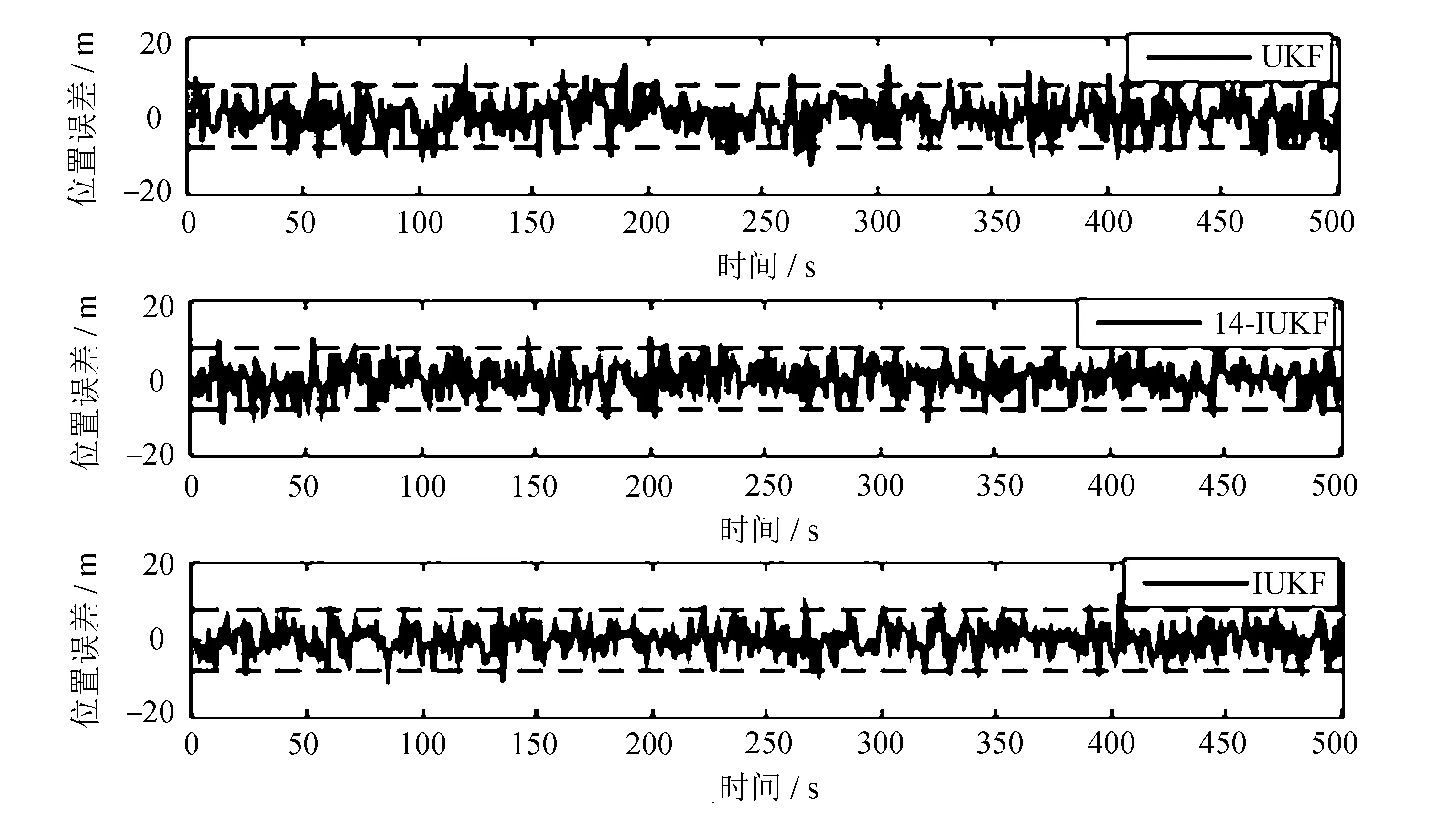
(b) 北向

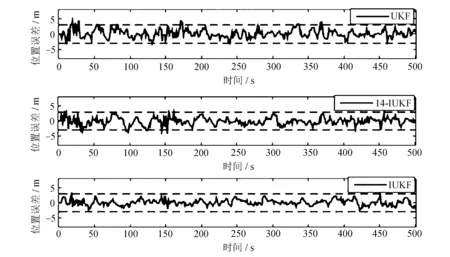
(c) 天向图2 东-北-天位置误差对比

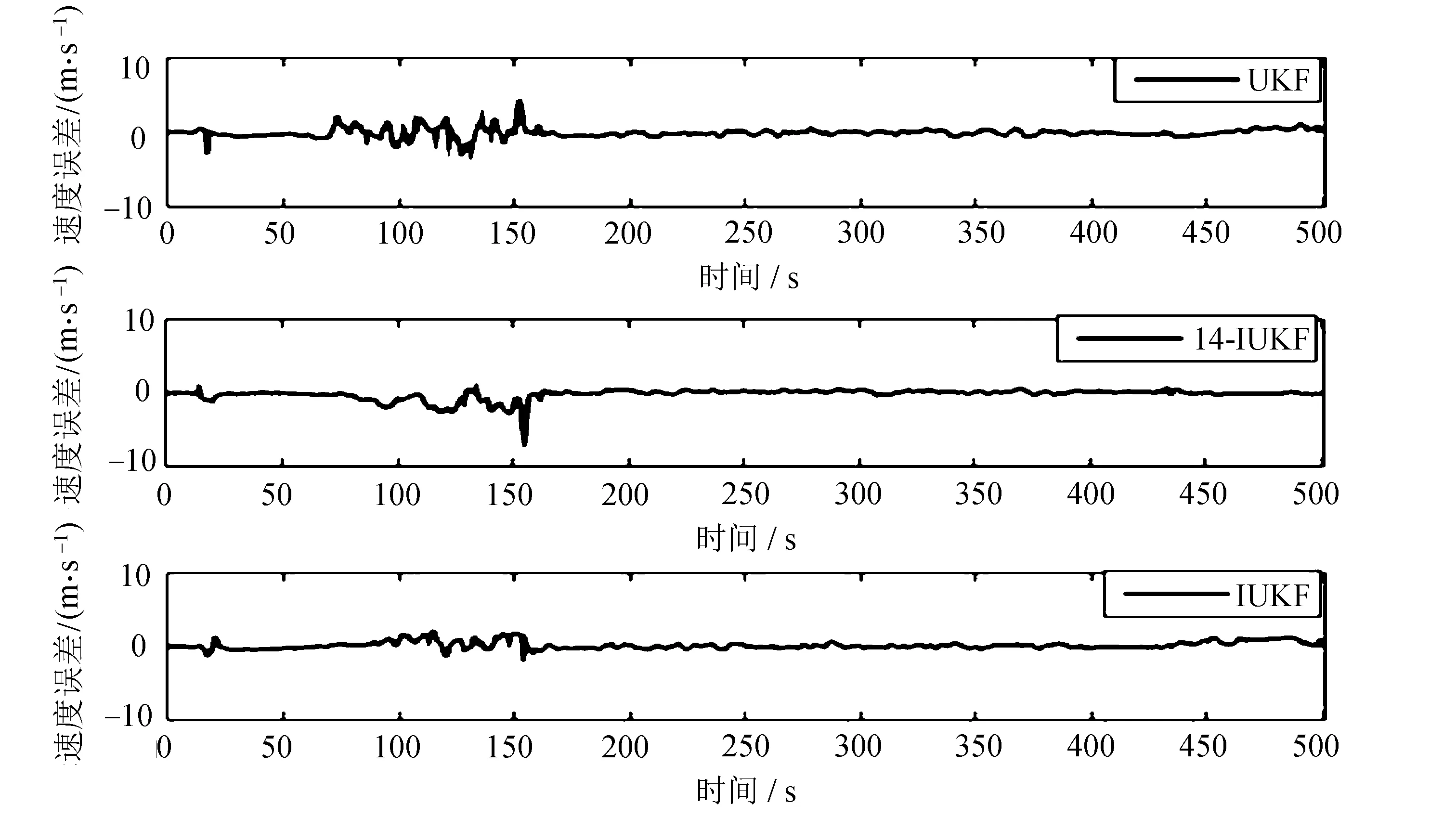
(a) 东向

(b) 北向

(c) 天向图3 东-北-天速度误差对比

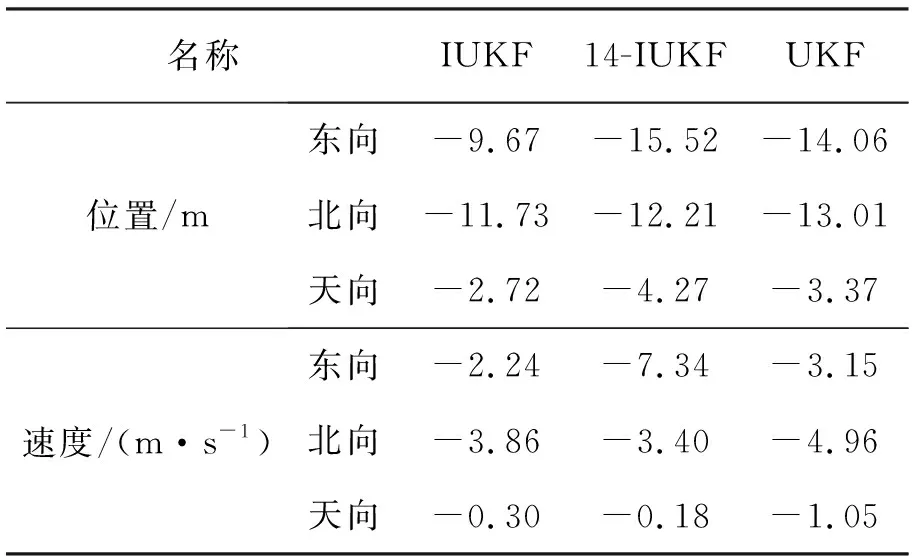
表3 最小误差对比

从表2和表3最大误差、最小误差的数值对比可以看出，IUKF在速度方面三个方向的误差波动范围分别为2.45～-2.24、4.79～-3.86、0.39～-0.30。对比算法UKF在速度方面三个方向的误差波动范围分别为4.46～-3.15、5.92～-4.96、0.75～-1.05。对比算法14-IUKF在速度方面三个方向的误差波动范围分别为0.76～-7.34、8.11～-3.40、0.16～-0.18。

IUKF在位置方面三个方向的误差波动范围分别为12.86～-9.67、12.13～-11.73、3.73～-2.72。对比算法UKF在速度方面三个方向的误差波动范围分别为16.78～-14.06、13.62～-13.01、4.59～-3.37。对比算法14-IUKF在速度方面三个方向的误差波动范围分别为13.36～-15.52、12.44～-12.21、2.97～-4.27。

均值误差对比见表4。

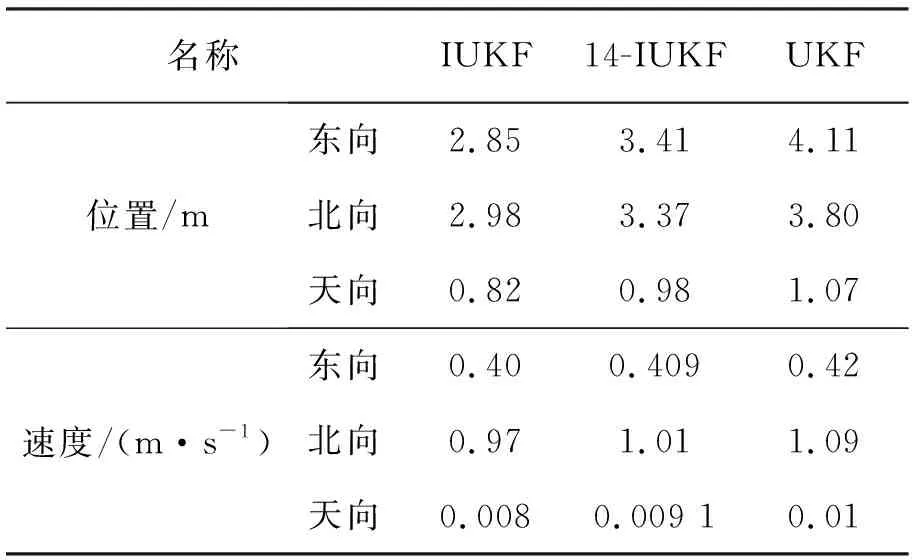
表4 均值误差对比

从表4三种算法的均值误差对比可以得到，文中提出的IUKF相比UKF，在位置的三个方向上，均值误差分别降低了30.66%、21.58%、23.36%；在速度的三个方向上，均值误差分别降低了4.76%、11.01%、20%。提出的IUKF相比14-IUKF在位置的三个方向上，均值误差分别降低了16.42%、11.57%、16.33%；在速度的三个方向上，均值误差分别降低了2.25%、3.96%、11.09%。由最大、最小值误差以及均值误差进一步证实了文中提出的IUKF整体滤波效果更优于UKF以及14-IUKF。

仿真时间对比见表5。

表5 仿真时间对比

从表5三种算法的仿真时间上看，IUKF相比UKF仅增加了0.193 s，相比14-IUKF仅增加了0.137 s。

4 结 语

提出面向GPS/INS组合导航的IUKF算法研究，通过实验仿真对比IUKF、UKF及14-IUKF的位置误差、速度误差可看出，IUKF算法可以有效改善因系统不确定性干扰导致的整体滤波的精度下降及发散问题。其仿真时间相比对比算法也并未明显增加，从而也保障了滤波的实时性。因此，文中提出的IUKF应用于GPS/INS组合导航中具有一定的研究意义。