基于带缺失PISA数据对中国学生科学素养的诊断分析

张笑笑， 单 娜

(1.长春工业大学 数学与统计学院， 吉林 长春 130012；2.东北师范大学 心理学院， 吉林 长春 130024)

0 引 言

立德树人是中国教育的根本任务，而发展核心素养是进行“立德树人”这一任务的重要举措，以核心素养为基础的教学与测评是中国素质教育深化改革面临的重要问题[1]。 科学素养是学生核心素养的关键成分，是培养高素质国民和促进社会高质量发展的重要基础[2]。科学素养的概念随着时代的发展而不断发生变化，为了对科学素养进行客观地测量与评价，国际学生评估项目(Programme for International Student Assessment,PISA)在《PISA2015科学框架草案》中指出,科学素养指作为一个有反思意识的公民能够参与讨论与科学有关的问题，提出科学见解的能力,包括三种主要的科学能力：1)科学地解释现象；2)评价和设计科学探究；3)科学地解释数据和证据。 PISA是经济合作与发展组织(简称OECD)举办的国际大规模测验，其测评设计十分严谨，对试题编制、测评框架都做了详细论证和考察，可以保证测评结果的科学性，是当前最主要的国际教育评价项目之一。

近年来，很多学者研究了PISA对学生科学素养的测评问题。刘克文等[3]从PISA2015科学素养测试内容及特点进行分析，梳理了科学素养这一概念的发展，指出PISA2015更加注重科学知识的建立过程和认知上的评价;黄鸣春等[2]对2000-2018年PISA科学素养测评体系设计进行分析，发现试题整合了知识、能力和情景三方面，在测评方面具有先进性，能够为参与国教育改革提供参考;李川[4]从PISA2015科学素养测试公开试题的特点进行分析，建议在实际的科学教学中，应该加强学生对科学本质的理解。针对PISA数据的统计分析，目前采用的研究方法主要包括经典测量理论[5]和项目反应理论[6]，并且对数据中的缺失值没有进行有效处理。因此，需在PISA科学素养的测评框架下发展新的数据分析方法来实现对科学素养准确而全面的评估。

1 理论和模型

1.1 理论介绍

基于经典测量理论和项目反应理论对学生科学素养的评估，主要关心学生宏观层次的能力水平，而没有对学生内部知识结构和加工技能进行评估，具有相同能力的学生可能具有不同的认知结构和加工技能[7]。为了解学生知识结构和加工技能的掌握状态，认知诊断模型应运而生。目前，已经有100多种认知诊断模型，例如线性Logistic模型、规则空间模型、融合模型和DINA模型等。其中，DINA模型主要用于0-1评分数据，因其具有较高的诊断率，模型易于理解以及操作简单被广泛使用。例如韩乐艳[8]使用DINA模型对初中物理教学设计和应用进行研究，发现DINA模型不仅提高了补救教学的针对性，而且提升了学生的学习效率；张焕[9]在高中“氧化还原反应”学习中利用DINA模型进行了诊断分析，从而更好地了解学生的知识掌握状态，并据此给出补救性的建议。

因此，本研究使用DINA模型对PISA2015数据所反映的中国学生科学素养进行诊断分析，为中国学生科学素养的评估和提升提供参考。

1.2 DINA模型

在进行DINA模型介绍时,需要了解以下两个定义。

1.2.1Q矩阵

学生内部的认知属性是无法观察到的，Q矩阵描述了测验题目和认知属性之间的关系。Q矩阵由I行K列组成，行表示测验题目，列表示认知属性，矩阵的元素是0或1。qik表示Q矩阵的第i行第k列元素，qik=1表示题目i考察了属性k;反之，qik=0。

1.2.2 属性掌握模式

若考察K个独立属性，则有2K种属性掌握模式。例如3个独立属性，即K=3，则共有8种属性掌握模式，分别记为(000, 100, 010, 001, 110, 101, 011, 111)，其中“000”表示3个属性均未掌握，“100”表示只掌握第1个属性，其他类似。

令Yni为学生n(n=1,2,…,N)在题目i上的作答反应，其中Yni=1表示学生n正确作答题目i，Yni=0表示学生n错误作答题目i。在DINA模型中，属性掌握状态和观察到的题目之间的关系可以表示为

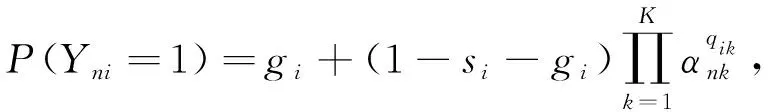
(1)

式中：P(Yni=1)----学生n在题目i上的正确作答概率;

si----失误参数;

gi----猜测参数;

αnk----学生n在属性k上的掌握状态，αnk=1表示学生n掌握属性k，αnk=0表示学生n不掌握属性k;

qik----Q矩阵的元素。

在DINA模型中，由学生的属性掌握状态αk和Q矩阵可以得到一个潜在的反应向量ηni，表示为

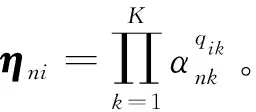
(2)

ηni=1表示学生n掌握了正确回答题目i所需的所有属性，否则,ηni=0。

但在现实情况下，学生作答时可能会遇到两种情况:

1)由于外界干扰，即使学生掌握了作答题目的所需属性，也可能因为失误而答错题目；

2)尽管学生没有掌握作答题目所需属性，仍可能因为猜测而答对题目。

在DINA模型中，题目i的失误参数si定义为

si=P(Yni=0|ηni=1)，

(3)

表示学生n掌握了题目i所需的属性而答错题目i的失误概率。

题目i的猜测参数gi定义为

gi=P(Yni=1|ηni=0)，

(4)

表示学生n未掌握题目i所有必需属性而猜对该题的猜测概率。

DINA模型只涉及“失误”参数和“猜测”参数，操作简单，易于理解，在实际应用中十分广泛。虽然DINA模型可以通过边际最大似然估计法得到参数的无偏估计，但是该方法无法解决数据中的缺失值问题[10]。文中采用贝叶斯MCMC算法实现对DINA模型的参数估计，因此可以有效地解决数据中的缺失问题[11]，并使用R软件中的R2jags包调取JAGS软件来实现贝叶斯MCMC参数估计[12]。

2 实证分析

2.1 数据描述

PISA于2000年开始实施，每三年进行一次，测试对象年龄为15～16岁，必须是接受学校教育的学生，以便了解完成义务教育之后的学生是否具备适应未来生活的能力。测试从三个方面进行，每次测试以阅读素养、数学素养和科学素养其中的一个领域为主，实施的第一年以阅读素养为主，2006年和2015年都以科学素养为主。

PISA2015科学素养示意图如图1所示。

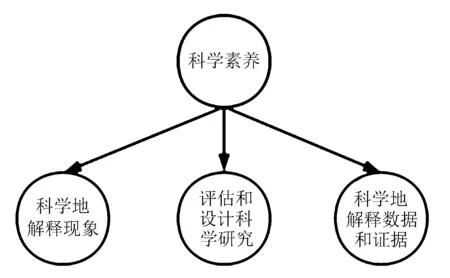
图1 PISA2015科学素养示意图

《PISA2015技术报告》[13]把科学素养解读为三种主要的科学能力：

1)科学地解释现象；

2)评估和设计科学研究；

3)科学地解释数据和证据。

使用文献[13]题池分类(2015 field trial and main survey cluster)中S02所包含的18道测试题目中的中国样本，共有957名学生，将数据中“not reached”和“no response”设定为缺失值NA，因为在实际作答时，往往会出现数据缺失的情况，如果直接删除缺失数据，会导致评估结果不准，而全贝叶斯MCMC算法可以根据其他参数的估计值计算出缺失值的后验分布，这是一种“自动填补”过程，无需做其他设定。此外，在这18道题目中，有一个三级评分题目，即DS498Q04，将它转化为二级评分数据，即0→0，1→0，2→1。最终得到学生n=957在i=18个题目上的二级评分数据。属性与题目之间的对应关系(即Q矩阵)见表1。

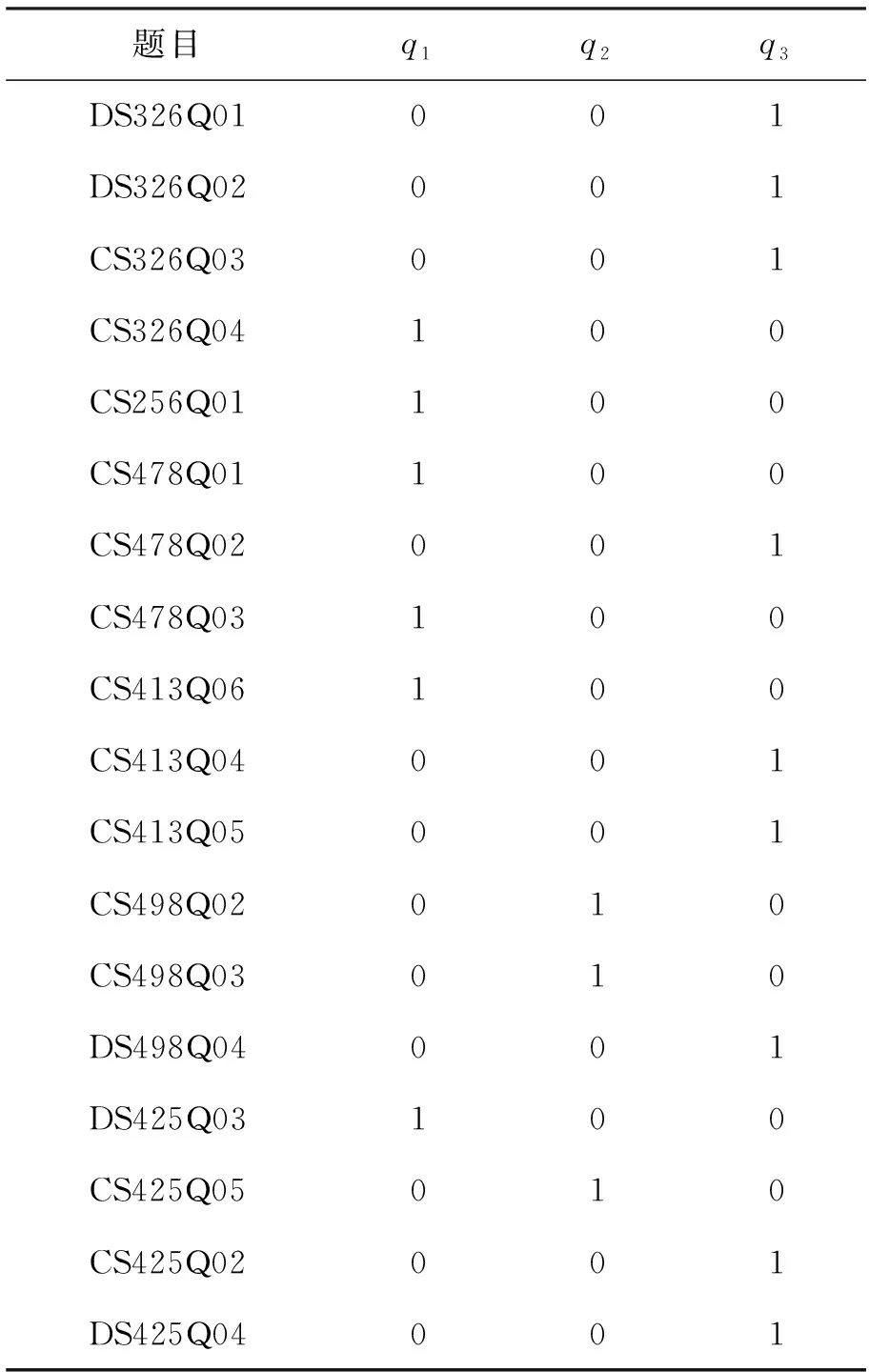
表1 PISA2015题目的Q矩阵

2.2 结果分析

全体学生各题目得分率见表2。

表2 全体学生各题目得分率 %

首先计算全体学生在每个题目上的得分率，可从整体把握每个题目的作答情况。由表2可以得知学生在题目CS256Q01的得分率为89.8%，表明大部分学生都答对了该题目，DS326Q01、DS326Q02、CS326Q03、CS478Q02、CS478Q03、CS413Q06、CS413Q05、DS498Q04、CS425Q05和CS425Q02的得分率分别为67.3%、72.0%、51.0%、51.8%、70.6%、52.1%、76.8%、65.5%、66.9%和62.4%，表明一半以上学生在这几个题目上都能答对，CS478Q01、CS413Q04、CS498Q02、CS498Q03和DS425Q03的得分率在40%～50%，表明答对这几个题目的学生人数不足一半，CS326Q04和DS425Q04的得分率分别为19.2%和27.4%，表明大部分学生不能正确作答这两个题目。由此可见，学生在题目CS326Q04和DS425Q04所测试的内容上存在困难。

使用DINA模型对PISA2015科学素养数据进行拟合的过程如下，使用两条马尔可夫链，每条链包含10 000次迭代，其中预热5 000次迭代，稀疏值1，最终剩余10 000次迭代用于参数估计。使用Brooks S P等[14]提出的潜在量尺缩减因子(PSRF)进行参数估计收敛性判断，文中所有参数的PSRF值均小于1.2，表示参数估计已收敛。模型-数据拟合值见表3。

表3 模型-数据拟合值

表3中ppp为0.4，说明模型拟合数据较好。

后验预测概率ppp越接近0.5,表明模型拟合数据效果越好;ppp<0.05或ppp>0.95,表明模型拟合数据效果不好。

使用DINA模型对PISA2015数据进行分析后得到的参数估计值见表4。

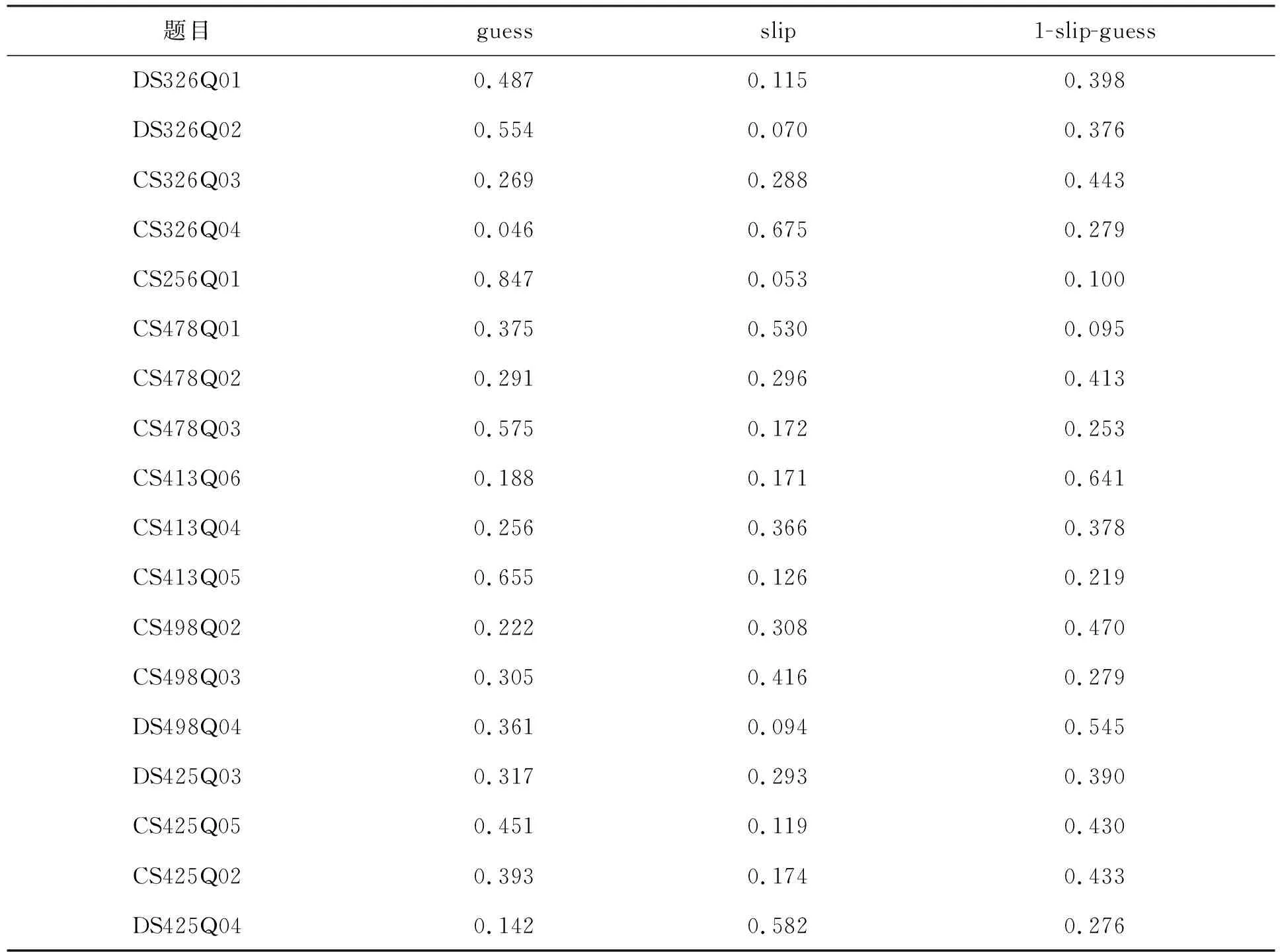
表4 测试题目的参数估计值

一般认为猜测参数和失误参数小于0.4，1-slip-guess>0说明DINA模型的诊断是有效的。从表4可以看出，1-slip-guess均大于0，失误参数和猜测参数大部分都小于0.4，失误参数的平均值为0.269，猜测参数的平均值为0.374，说明DINA模型拟合效果较好。从表中可以看到，CS256Q01和CS413Q05的猜测值分别为0.847和0.655，说明学生在这两个题目上的猜测参数过大，学生可能没有掌握这两个题目所需的属性；CS326Q04和DS425Q04的失误参数分别为0.675和0.582，学生在这两个题目上的失误参数大，有可能学生掌握了这两个题目所需的属性,但是由于受到干扰，导致这种情况产生。

认知诊断可以对学生的属性掌握状态提供详细的诊断报告，使学生了解自己的薄弱之处, 从而进行有针对性的补救。比如两个学生281和611的总分相同，都是12分，但他们的属性掌握模式不同，总分相同的两个学生的属性掌握模式见表5。

表5 总分相同两个学生的属性掌握模式

由表5可以看出，两个学生的总分相同，但是他们在每个题目上的作答反应不尽相同。两个学生的属性掌握模式也不同，学生281掌握了属性q2和q3，没有掌握属性q1，所以要针对属性q1进行加强学习；学生611掌握了属性q1和q2，没有掌握属性q3，所以要加强属性q3的学习。

3 结 语

基于DINA模型分析PISA2015中国学生科学素养数据，能够为参与这一测评学生的科学素养状态提供详细的诊断分析，从而可以根据每一名学生的科学素养掌握情况进行针对性地训练，为中国学生科学素养的提高和素质教育改革提供参考。