贝叶斯项目反应模型及nimble实现

于铃玉， 曹 蕾， 张婉婷， 李佳伟

(长春工业大学 数学与统计学院， 吉林 长春 130012)

0 引 言

对于项目反应模型，从连接函数角度来看，常用的连接函数有logistic和probit；从参数角度来看，有单参数、双参数和三参数的项目反应模型，并且它们均可以用logistic和probit连接函数。Leventhal Brian C等[1]、张雪[2]、张国红[3]、Bolsinova M等[4]项目反应模型的连接函数为logistic连接函数。Lu J等[5]、Bolsinova M等[6]项目反应模型是probit连接函数。

文中首先介绍了单参数、双参数和三参数的项目反应模型。其次，分别采用连接函数logistic和probit对单参数、双参数和三参数的项目反应模型进行计算并比较。应用了DIC和LPML两个模型方法，DIC小说明模型好，LPML大说明模型好。最后，在实证研究部分，通过计算每个模型的DIC值和LPML值得出结论，当连接函数为logistic的双参数模型最好，因为DIC值最小，同时LPML值最大。由于贝叶斯计算项目反应模型存在一定困难，链特别长，所以针对实证研究的程序是由nimble包编写的，nimble包的语法结构类似于WinBUGS和JAGS，但是比WinBUGS和JAGS更灵活，因为编程时用C++代码，所以运算速度快[7]。

1 模型分析

1.1 模型的建立

被试者用i(i=1,2,…,N)表示，题目用j(j=1,2,…,J)表示。Yij表示第i个人对第j道题目的回答，Yij=1表示回答正确;Yij=0表示回答错误。假定θi为第i个人的能力参数，用单参数的logistic连接函数表示第i个人答对第j个题目的概率为[8]

用双参数的logistic连接函数表示第i个人答对第j个题目的概率为

pij=P(Yij=1|θi,aj,bj)=

用三参数的logistic连接函数表示第i个人答对第j个题目的概率为

pij=P(Yij=1|θi,aj,bj,cj)=

式中：aj、bj、cj----分别表示项目j的区分度参数、难度参数和伪猜测参数。

假定aj(j=1,2,…,J)相互独立，bj(j=1,2,…,J)，cj(j=1,2,…,J)相互独立，且假设它们的先验logaj～N(0,1),bj～N(0,1),cj～Beta(4,12)。

此外，还可用单参数的probit连接函数表示第i个人答对第j个题目的概率为[9]

pij=P(Yij=1|θi,bj)=Φ(θi-bj)，

用双参数的probit连接函数表示第i个人答对第j个题目的概率为

pij=P(Yij=1|θi,aj,bj)=

Φ(ajθi-bj)，

用三参数的probit连接函数来表示第i个人答对第j个题目的概率为

pij=P(Yij=1|θi,aj,bj,cj)=

cj+(1-cj)Φ(ajθi-bj),

式中：Φ----正态累积分布函数。

1.2 模型参数的贝叶斯估计

对于单参数的连接函数logistic模型，假设yi=(yi,1,yi,2,…,yi,J)′，第i个人反应部分的似然函数为

双参数的连接函数logistic模型的似然函数为

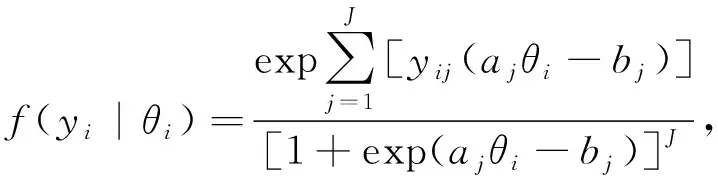
(1)

三参数的连接函数logistic模型的似然函数为

f(yi|θi)=cj+

当单参数的连接函数为probit模型时，第i个人反应部分的似然函数为

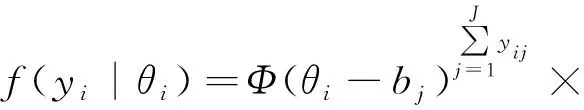
双参数的连接函数为probit模型的似然函数

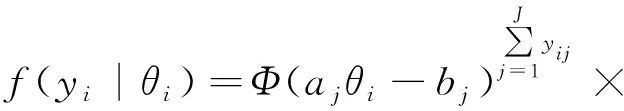
三参数的连接函数为probit模型的似然函数

f(yi|θi)=cj+

根据Linden W[10]的思想进行局部独立性假设,令

γ=(a1,a2,…,aJ;b1,b2,…,bJ;θ1,θ2,…,θN)′。

我们以连接函数为logistic的双参数项目反应模型为例进行计算，利用式(1)得到N个人的联合似然函数为

γ的后验分布为

(2)

式中：m(y)----正则化常数(normalizing constant)，

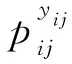
π(aj)----aj的先验;

π(bj)----bj的先验;

π(θi)----θi的先验。

它们具体的先验在前面部分已给出。

1.3 模型选择方法

文中用到的模型选择方法为DIC准则和LPML。由于DIC可以在多元模型的固定或随机部分不同的模型之间进行选择，而不必指定模型参数的数量。DIC是由Spiegelhalter D J等[11]提出的,它是一种可以用来模型拟合以及模型复杂性测量的方法，DIC准则是在偏差的后验分布基础上建立的，其函数表达式为：

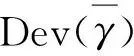
PD----有效参数的个数;

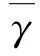
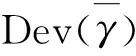
另一个评估模型相对拟合效果的方法是基于Chen M H等[13]、Gelfand A E等[14]的思想，通过采用条件预测纵坐标(Conditional Predictive Ordinate, CPO)指标计算LPML，设

则CPO的蒙特卡罗估计为如下形式

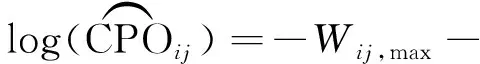
式中：r----MCMC算法的第r次迭代，r=1,2,…,R;

R----总迭代次数。

LPML值越大，表明所选择的模型效果越好。

2 实证研究

2.1 数据结构

采用国际学生评估项目2015年数据(PISA)。数据中有548(N=548)个学生，每个人回答16(J=16)道题的考试，计算机会自动记录并存储被试者答题正确与否。基于单参数、双参数和三参数的项目反应模型，进行30 000次迭代，烧掉前25 000次。被试者答对题目正确与否的部分数据见表1。

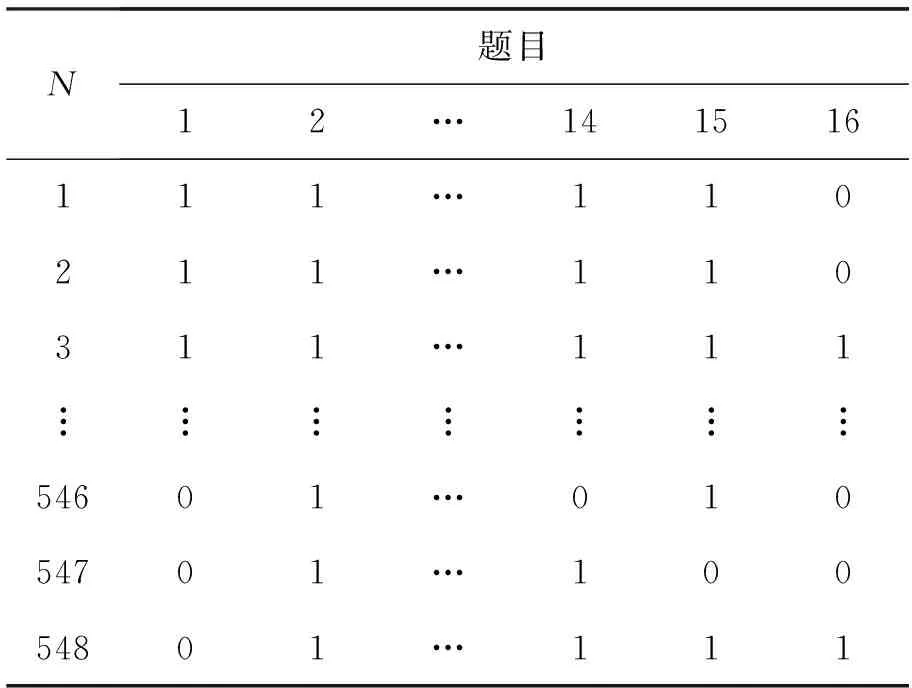
表1 被试者答对题目正确与否的数据

2.2 项目反应模型的nimble实现(以三参数logistic模型为例)

res6 <- read.csv("res61.csv", header=FALSE)

res6=as.matrix(res6)

N=length(res6[,1])

J=length(res6[1,])

nitem=rep(J,N)

cuni=cumsum(nitem)

id=cuni-nitem

item_index=matrix(,N,J)

for (i in 1:J)

{item_index[,i]=i}

y=rep(0,J*N)

for (i in 1:N){

y[((i-1)*J+1):(i*J)]=res6[i,]

}

velocity=rep(1,N*J)

irt<-nimbleCode({

for (j in 1:J){

for(i in 1:N){

y[id[i]+j]～dbern(prob[id[i]+j])

prob[id[i]+j]<-c[j]*velocity[id[i]+j]+(1-c[j]*velocity[id[i]+j])*(exp(a[j]*velocity[id[i]+j]*theta[i]-b[j]*velocity[id[i]+j])/(1+exp(a[j]*velocity[id[i]+j]*theta[i]-b[j]*velocity[id[i]+j])))

}

a[j]～dlnorm(0, sdlog=1)

b[j]～dnorm(0, sd=1)

c[j]～dbeta(4,shape1 = 12)

}

for (i in 1:N){

theta[i]～dnorm(0,1)

}

})

data <- list( y =y)

constants <- list(J=J,N = N,id=id,nitem=nitem,velocity=velocity)

inits <- list(theta=rep(0,N),a=rep(0.5,J),b=rep(0,J),c=rep(0.1,J))

jointmodel <- nimbleModel(irt,

data = data,

constants = constants,

inits = inits,

check = FALSE)

mcmc.out2<- nimbleMCMC(model = jointmodel,

niter = 30000, nchains = 1, nburnin =25000,thin=1,monitors = c('a','b','c','theta'), summary = TRUE,WAIC = TRUE,setSeed = 10)

第一部分程序中的N表示考生人数，J表示题目数量，为了让模型的维度一致，方便编程，所以引入了velocity[id[i]+j]，应用nimble包，先写出三参数logistic模型，然后给出参数服从的分布以及初值，其中，项目区分度参数logaj～N(0,1)，猜测参数bj～N(0,1)，迭代了30 000次，烧掉了前25 000次。

linsam=read.csv(file='res_only_logistic_sam_lin1.csv')[,-1]

loglisampler=rep(0,nusample)

prob<- cij+(1-cij)*(exp(aijtheta-bij)/(1+exp(aijtheta-bij)))

coran=which(y==1)

loglikelir= sum(log(prob[coran]))+sum(log(1-prob)[-coran])

loglikelir=(-2)*loglikelir

bigtheta3= bigzeta3=rep(0,cuni[N])

cpoi=matrix(rep(0,N*5000),5000)

probb=matrix(rep(0,nusample*cuni[N]),nusample)

loglisampler=rep(0,nusample)

for (k in 1:5000){

aj<-as.numeric(linsam[k,1:16])

bj<-as.numeric(linsam[k,17:32])

cj<-as.numeric(linsam[k,33:48])

theta<- as.numeric(linsam[k,49:(49+N-1)])

bij=rep(bj,N)

aijtheta=c(t(outer(theta,aj,FUN="*")))

cij=rep(cj,N)

for (qq in 1:(N-1)){

beg1=cuni[qq]+1

end1=cuni[qq+1]

bigtheta3[beg1:end1]=rep(theta[qq+1],nitem[qq+1])

}

beg1=1

end1=nitem[1]

bigtheta3[beg1:end1]=rep(theta[1],nitem[1])

probb[k,]<- cij+(1-cij)*(exp(aijtheta-bij)/(1+exp(aijtheta-bij)))

for (i in 1:(N-1))

{ beg1=cuni[i]+1

end1=cuni[i+1]

aa=which(y[beg1:end1]==1)

bb=probb[k,beg1:end1]

cpoi[k,i+1]=1/(prod(bb[aa])*prod(1-bb[-aa]))

}

beg1=1

end1=nitem[1]

aa=which(y[beg1:end1]==1)

bb=probb[k,beg1:end1]

cpoi[k,1]=1/(prod(bb[aa])*prod(1-bb[-aa]))

loglisampler[k]= sum(log(probb[k,][coran]))+sum(log(1-probb[k,])[-coran]) }#k

loglisampler=(-2)*loglisampler

EDEr1=mean(loglisampler);

PDICr1=EDEr1-loglikelir

DICr1=loglikelir+2*PDICr1

LPML<- sum(log(1/apply(cpoi,2,mean)))

第二部分程序是为了计算三参数logistic模型的DIC、PD和LPML值，linsam是读取第一部分产生的项目反应模型的MCMC，loglikelir是计算这个模型的似然函数，最后通过for循环计算DIC、PD和LPML值。

2.3 结果分析

不同情况下的DIC、PD和LPML值见表2。

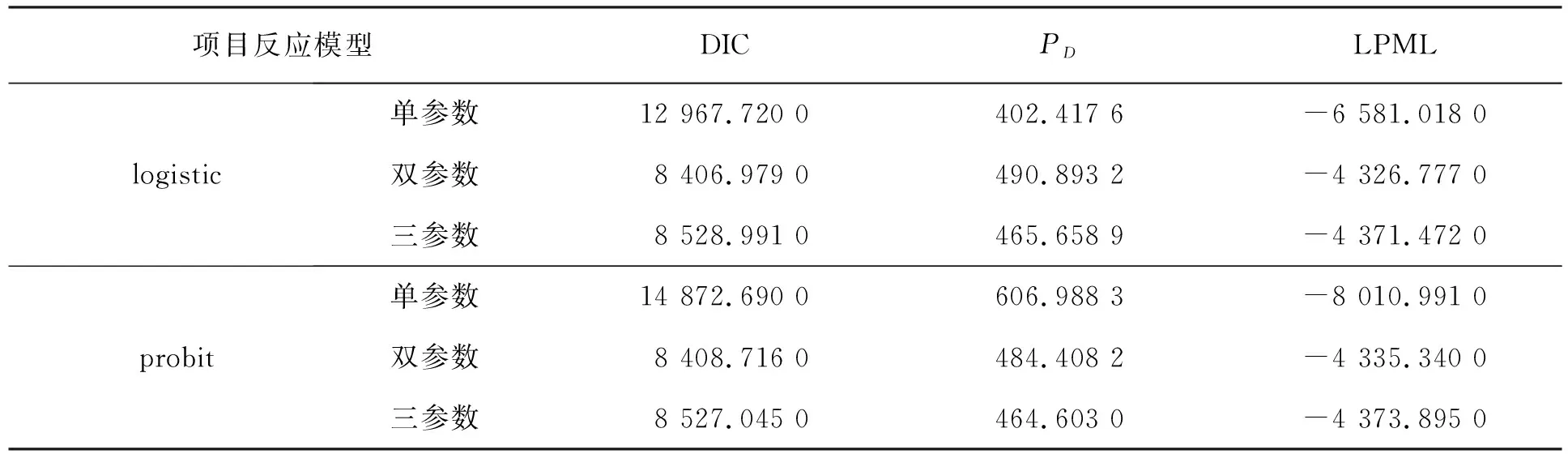
表2 不同情况下的DIC、PD和LPML值

表中通过比较这几种情况的DIC值和LPML值发现，连接函数为logistic的双参数项目反应模型的DIC值最小，LPML值最大，模型表现最好。单参数的项目反应模型的DIC值都较大，模型表现不好。三参数的项目反应模型比双参数项目反应模型增加了伪猜测参数，正常情况下，DIC值应该增加32左右，但结果增加了100多，所以增加伪猜测参数的项目反应模型表现也不好。

3 结 语

基于国际学生评估项目2015年数据(PISA)，采用单参数、双参数和三参数的项目反应模型分别进行建模，同时在单参数模型、双参数模型和三参数模型下，分别考虑logistic连接函数和probit连接函数，通过计算6种模型的DIC值和LPML值得出结论，连接函数为logistic双参数项目反应模型的DIC值最小，并且LPML值最大，此模型表现最好。