塔脚板结构强度与底板接触应力分析
蒋童,徐海潮,张树林,肖奉英,黄模佳,晏洪
(1.南昌大学工程力学系,江西 南昌 330031;2.中国能源建设集团安徽省电力设计院有限公司,安徽 合肥 230601)
随着特高压输电线路的迅速发展,对输电铁塔塔脚板的安全性要求越来越高[1]。塔脚板为铁塔底部角钢与基础间的连接节点,塔脚板的可靠性对铁塔结构整体的安全性至关重要。塔脚板由底板、靴板等板件焊接而成,铁塔底部角钢通过螺栓与塔脚板靴板连接,底板通过地脚螺栓与基础连接。陈勇等[2]对特高压导线和塔结构的设计进行了综述,陈绍番等[3]研究了钢结构的螺栓连接,沈国辉等[4]利用接触单元对螺栓的挤压、剪切及其预紧力的作用进行了有限元模拟仿真;《架空输电线路杆结构设计规范规定》[5]中给出了塔脚板受拉和受压时的弯曲应力和结构尺寸计算式;张元良等[6]认为利用规范得到的弯曲应力进行厚度设计过于保守,材料潜力不能充分发挥。刘俊卿等[7]对八地脚螺栓塔脚板进行理论及有限元分析,给出了塔脚板底板的厚度表达式;杨攀等[8]对八地脚螺栓塔脚板的传力机制进行了研究,给出了该塔脚板底板厚度设计的计算式;殷黎明等[9]开展了塔脚板的有限元分析计算,对文献[5]厚度设计的计算式进行了修正,解决了规范[5]中厚度设计过于保守的问题。肖奉英[10]等基于里兹法对塔脚板进行内力计算给出了塔脚板最大弯矩的解析解。塔脚板底板受到的压力往往大于拉力,压载荷工况下塔脚板底板与基础间的接触应力并非均匀,离靴板近的底板接触应力大,离靴板远的底板接触应力小,底板与基础接触应力的这种分布极不均匀是文献[5]中所给出的受压底板厚度设计偏于保守的原因。
本文对四地脚螺柱塔脚板的受压工况进行了强度分析:首先分析铁塔底部角钢与靴板间螺栓的连接强度,研究了群排螺栓的每个螺栓载荷分配规律,并对群排螺栓位置布置提出了合理建议;考虑底板与基础接触应力的不均匀性,利用里兹法[11-12]给出塔脚板底板的弯曲应力表达式,并将该表达式应用于底板的强度校核和厚度设计。有限元仿真计算结果与里兹法给出的弯曲应力表达式计算结果一致。本文的结果可作为塔脚板底板厚度设计的依据。
1 寻找塔脚板结构强度的关键点
1.1 塔脚板的构件组成及网格划分
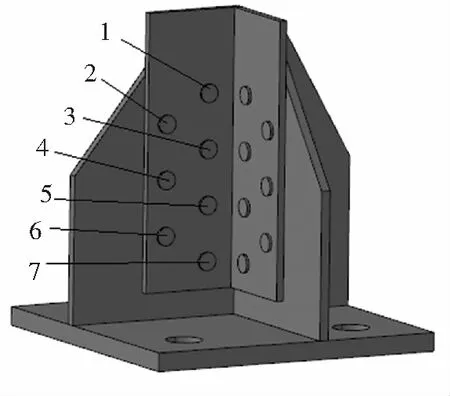
塔脚板由底板、靴板、角钢、螺栓组成,选取(如图1所示)四地脚螺栓塔脚板作为有限元仿真计算对象,采用C3D20R单元对塔脚板模型进行网格划分,钢材的泊松比ν为0.3,弹性模量E为2.06×105MPa,在角钢上方施加330 kN的压荷载,塔脚板底板与基础间采用接触元,靴板与角钢间的螺栓连接也采用接触元[4]处理。
1.2 塔脚板的应力强度分析
通过有限元仿真计算,可得塔脚板各区域的等效应力云图如图2所示。在压工况下,角钢、靴板通过连接螺栓连接,螺栓与孔的挤压应力大。
塔脚板各部分等效应力见表1,可知:
(1) 角钢处的挤压应力达569 MPa,但接触力属于压力,对塔脚板破坏的影响有限;
(2) 螺栓处的最大等效应力达到373 MPa,但螺栓的强度高,螺栓不会发生断裂破坏;
(3) 螺栓连接处的应力相对偏大,需要找出角钢和靴板群排螺栓连接的各螺栓载荷分配规律,这对了解塔脚板连接螺栓的安全性至关重要;
(4) 底板承受的弯曲应力偏小,底板钢材的潜力没有充分发挥,修正塔脚板底板的厚度设计公式势在必行。
2 角钢和靴板间群排连接螺栓的载荷分配
2.1 各螺栓载荷分配比的理论分析
由图3和表1的结果可知,角钢与靴板间群排连接螺栓工作应力大,对结构整体安全性影响也大,螺栓受剪模型如图3所示。
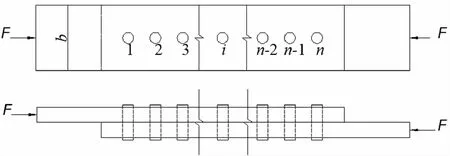
图3 螺栓受剪简化模型Fig.3 Simplified model of bolt shear
简化模型由上盖板、下盖板和螺栓连接组成,连接盖板厚度为t,螺栓半径为r,每两螺栓间距为l(其中l>r),连接盖板的宽度为b,盖板两端作用的荷载为F,对应螺栓所受剪力为Q1,Q2,…,Qn,如图4所示。
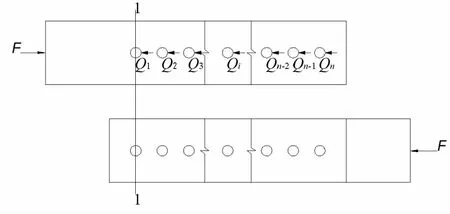
图4 螺栓受力分析模型Fig.4 Bolt stress analysis model
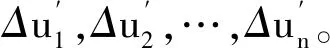
(1)
式中:L为板的长度;A1为板的横截面面积。
根据弹性力学中对小孔进行极坐标平面求解问题[13],杨昌对螺栓群力的分布研究[14]可得圆孔局部变形表达式为
(2)

(3)
由式(3)可得上盖板螺栓群的相对变形为
(4)
下盖板螺栓相对变形为
(5)
(6)
通过式(6)可得:当两螺栓之间的距离及螺栓半径一定时,其盖板的宽度越大,螺栓所受到的剪力大小就越趋于均匀;当盖板的宽度及螺栓半径一定时,两个螺栓之间的距离越小,螺栓所受到的剪力大小就越均匀;当盖板宽度及两螺栓间距一定时,螺栓半径越小其所受剪力越趋于均匀,螺栓半径越大则中间部位螺栓所受剪力越小;第1个与最后1个螺栓所受到的剪力相同。
2.2 螺栓群排布对螺栓受力影响的有限元数值分析
对常规塔脚板模型的螺栓群进行编号,如图5(a)所示。角钢两边总共14个螺栓,对该模型进行有限元分析,结果如图5(b)所示,每个螺栓所受剪力均不相同,最大与最小值相差较大,需探究合理排布螺栓个数与位置使得螺栓所受剪力趋于均匀。

(a) 塔脚板整体应力图

(a) 应变片编号 (b) 试验模型
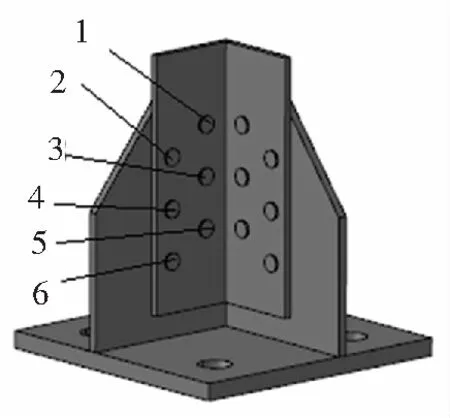
(a) 模型1
(a) 螺栓群编号图
通过计算结果分析可知,塔脚板在受压时,第1个螺栓与最后1个螺栓所受到的剪力最大,且剪力不相等,与式(6)的结果稍有不同,该原因主要由靴板上方宽度较小而下方宽度较大引起;处于中间的螺栓所受剪力较小,且剪力值比较接近,印证了解析解式(6)的合理性。
基于式(6)得到的结论,考虑螺栓可以并排式及错开式两种布置,在常规塔脚板尺寸相同的情况下,对螺栓不同位置排布进行建模分析,3种模型图如图6所示。
通过有限元仿真计算提取各模型的螺栓剪力,结果如图7所示。
由图7可以得到模型2比模型1的螺栓所受最大剪力小,即第1个螺栓靠近外端时优于第1个螺栓靠近内侧。模型3与模型1、模型2比较可知,当每排螺栓对称排布时,螺栓所受的剪力更加均匀。通过图7与图5比较可知,当螺栓个数减少时,螺栓所承受的最大剪力变化不大,且最大与最小剪力的差值减小,使得螺栓所受应力趋于均匀。
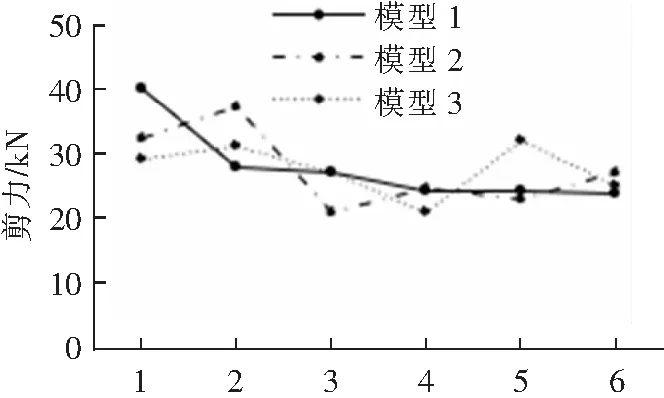
螺栓编号图7 6孔螺栓剪力Fig.7 6-hole bolt shear
2.3 试验数据对比
为验证理论分析及有限元计算的可靠性,因此对螺栓受力情况进行真实试验。如图8所示为塔脚板真实模型。

图8 塔脚板试验模型Fig.8 Tower foot test model
螺栓实际受力大小并不能直接测出,所以在通过测取连接螺栓附近变形大小从而得到螺栓的真实受力情况。图9所示为所贴应变片位置,为保证试验的可靠性,所以对两侧连接螺栓附近都贴有应变片,每侧都贴有9个应变片。
提取在330 kN作用下所产生的应变数据,将试验结果与有限元计算结果对比如图10所示。
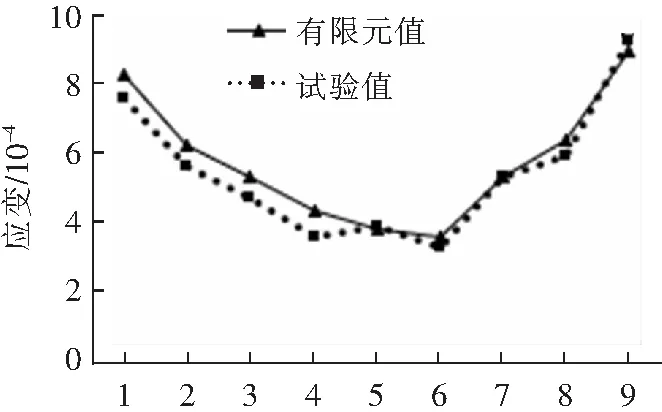
应变片编号图10 试验值与有限元值对比Fig.10 Test value is compared with the finite value
通过对比可知,试验值与有限元计算结果较为吻合,由图10可知,连接螺栓两端变形较大,而中间连接螺栓变形较小。
3 塔脚板底板弯曲强度分析
3.1 底板厚度理论解析解的推导
以常规四地脚螺栓塔脚板的压工况为例,进行大量有限元仿真计算,结果表明:塔脚板在受压时,其底板受到的大部分压力位于靴板附近,即受力范围主要为底板长度的1/3,如图11所画实线部分。
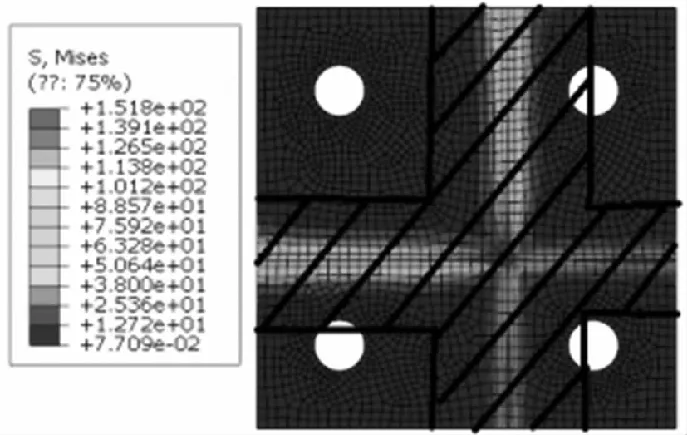
图11 底板应力云图Fig.11 Base plate stress cloud chart
基于规范公式的推导思路,不考虑底板上地脚螺栓的布置影响,且不以塔脚板的最大区格作为计算区格,将整个底板平均分为4部分,即每个区隔板宽为底板宽的一半,取底板的1/4进行研究。假设塔脚板受到的压力为N,其底板的板宽为2a,即取1/4底板后,其边长为a,模型的相邻两端固定,主要受力区间的均布荷载为q,得到的简化受压模型如图12所示。

图12 压工况方型塔脚板简化受力模型Fig.12 Simplified force model of square bottom plate under pressure condition
在工程中,塔脚板底板的板厚一般远小于底板的宽度,故可将塔脚板底板厚度设计视为薄板问题,利用里兹法对其进行求解。薄板底部所受的均布荷载为q(x,y),定义其变形位移为w,因此其薄板的微分方程为
(7)

以《2018年普通高中英语课程标准(实验)》和《2018年普通高等学校招生全国统一考试大纲的说明》的相关考查要求为导向;以教材为基础;以学生学情、2018年全国一卷试题特点和趋势以及学生在2018年高考全国I卷试题中所表现出来的突出问题为依据;以解决学生的实际问题、夯实学生的基础知识、提高学生运用英语知识的能力、加强学生学科核心素养的培养为目标,密切关注高考动态,制定实实在在的,行之有效的复习计划和方案,切实搞好高三英语一轮的复习工作,以适应新高考形势和要求。
由图12的边界条件可知该模型两相邻端为自由,另外两相邻端为固定,通过里兹法建立符合位移边界条件的位移w方程表达式
w=a1η1(x,y)+a2η2(x,y)+…+anηn(x,y)
(8)
式中:a1,…,an为所需求解的常数;η1(x,y),…,ηn(x,y)为已知的位移函数。为了使得到的工程解较为精确,选取10个位移函数进行求解并将方程进行无量纲化,使方程适用于不同尺寸的方形底板,方程可用矩阵的形式表示
w=aHTB
(9)
式中:H=[a1,a2,…,a10]T;B=[x2y2,x3y2,…,x2y5]T。
薄板受到的外力势能V为
(10)
薄板的形变势能为
(11)
薄板的系统总势能U满足
U=U1-V
(12)
由最小势能原理可知,在求解底板的真实位移w时,系统总势能U应为最小值,即对U的一阶变分为零,其方程为
δU=0
(13)
为了求得H矩阵,引进R、S矩阵,其计算方法为
(14)
其中
H=R-1S
(15)
利用式(15)对ai进行求导,通过Maple软件计算及理论推导。在求解最大弯矩M时,式(9)中只有矩阵B含有自变量,所以在此处对矩阵B进行求导,故最大弯矩求解公式为
(16)
通过计算推导,四地脚螺栓塔脚板在均匀受压情况下的工程解为
M=0.059qa2
(17)
根据理论公式M/W≤f(其中W为截面抗弯模量,f为材料抗压设计值)可求出底板厚度设计解析解
(18)
3.2 四地脚螺栓塔脚板模型的有限元数值计算
利用Abaqus软件对塔脚板进行有限元仿真计算,基于塔脚板底板为薄板这一理论,假定塔脚板使用材料为理想的弹性材料,选用三维壳元建模,所有模型均采用STRI65网格单元进行网格划分,材料的泊松比为0.3,弹性模量为2.06×105MPa,为了比较方便,此处将荷载q单位面积化为q1赋予特殊值进行计算,建立6个有限元模型,模型信息如表2所示。

表2 塔脚板模型信息Tab.2 Bottom plate model information
将有限元仿真计算所得到的应力值绘制成曲线,通过曲线图来比较塔脚板的应力分布状态和规律,曲线图如图13所示。
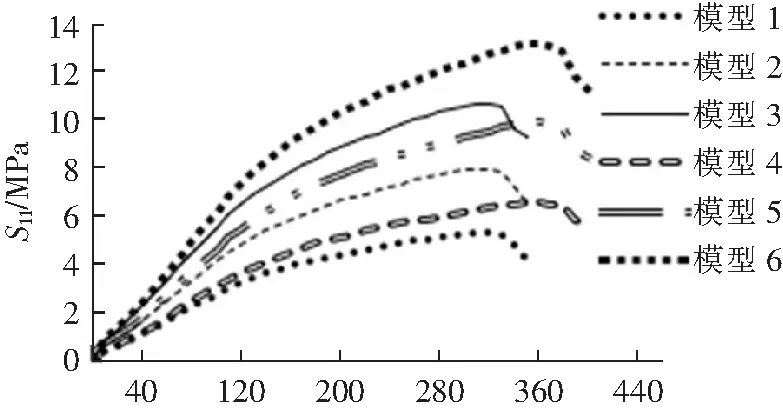
x/mm图13 压工况应力曲线图Fig.13 Stress graph for pressurized conditions
通过图13的应力比较可得,当塔脚板在受压时,随着荷载越来越大,其应力也会逐渐变大;由模型1、模型4的应力曲线可以得到,当塔脚板受到相同大小的压荷载时,底板面积越大,其所受到的应力也就越大,产生的变形也越大。通过应力图整体结果分析可得,在塔脚板底板受压时,底板受到的最大弯曲应力在其板的最边上即角钢与底板交界处,当底板长度越来越大,其所受的最大弯曲应力的位置也会随着板长增加向板外侧偏移。
3.3 四地脚螺栓塔脚板理论值与有限元数值计算值比较
通过前面分析,现将由里兹法推导的工程解所计算的理论值M0与有限元计算值进行比较,其计算结果如表3所示。
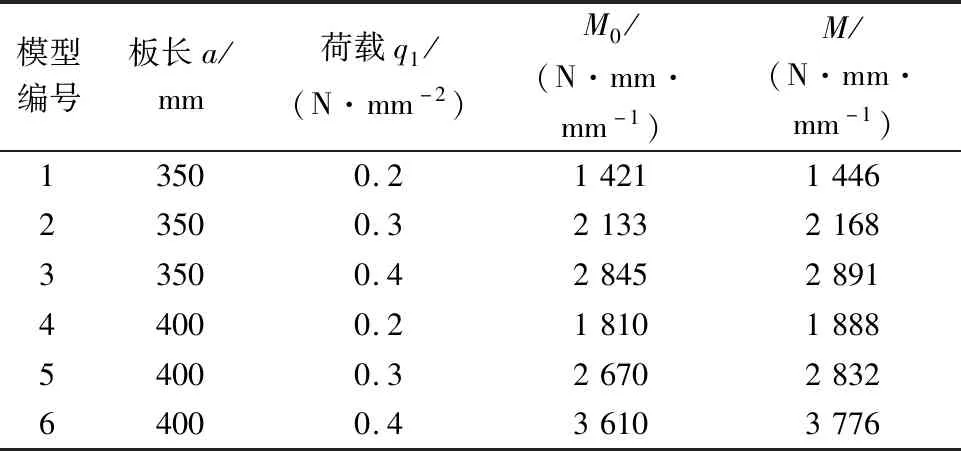
表3 有限元值与理论值比较Tab.3 Finite value is compared with the theoretical value
通过表3可得,当四地脚螺栓塔脚板处于压工况时,有限元计算结果与里兹法推导得到的理论值比较吻合,从而验证了解析解式(18)的合理性,式(18)对工程中有靴板塔脚板厚度设计具有一定的指导意义。
4 结论
(1)由理论分析发现当两个螺栓之间的距离一定时,其盖板的宽度越大,螺栓所受到的剪力大小就越趋于均匀;当盖板的宽度一定时,两个螺栓之间的距离越小,螺栓所受到的剪力大小就越均匀。
(2) 本文通过对螺栓有限元计算及试验分析,得到连接螺栓第1个和最后1个受到的剪力最大,且这两个螺栓所受的剪力较为接近,所以更加验证理论工程解及结论(1)的合理性。并且当靴板宽度一定时,可对螺栓群进行并排放置可使所受剪力趋于均匀。
(3) 本文通过里兹法理论推导,提出其底板厚度设计表达式,并且建立了6个有限元模型进行有限元模拟计算。本文所提出的解析解计算的结果与有限元计算结果基本吻合,从而验证了本文所提出的解析解的合理性,给目前工程中有靴板塔脚板底板厚度设计提供参考。
(4) 通过理论解析解及有限元计算发现,塔脚板在压工况时,底板面积越大,其所受到的应力也就越大,产生的变形也越大,故在满足承载力前提下,设计塔脚板底板时,建议将底板面积适当减小,而底板厚适当加大。

