钢芯铝绞线在张力与温度共同作用下的分层应力

豆云龙，包华，邵汉杰，兰志文，张盛强

(1.南昌大学工程力学系,江西 南昌 330031；2.中国能源建设集团安徽省电力设计院有限公司，安徽 合肥 230092)

钢芯铝绞线是架空导线的主要产品之一，钢芯和铝股共同承担导线张力[1]。实际工作中钢芯主要起增加强度的作用，铝绞线主要起传送电能的作用[2]。实际运行时，钢芯铝绞线在张力和温度共同作用下，截面应力会出现明显的分层效应。现有工程中均按照平均应力进行施工和设计计算，忽略了钢芯和铝股的自身性质不同、导线几何形状、挤压摩擦等的影响。分析导线在热力共同作用下应力分层效应，对钢芯铝绞线的安全设计与选用及抗疲劳性能研究具有重要参考价值[3]。

郑黎阳等[4]研究了铝绞线和钢芯铝绞线在受张拉时的理论模型，给出了在张力作用下绞线应力的计算方法。林建华等[5]通过有限元分析，模拟导线在运行过程中所受张拉应力后的应力分布规律。秦力等[6]考虑碳纤维复合芯导线的结构、材料特性,通过有限元分析,模拟分析了导线在实际运行过程中受到拉力、剪力和弯矩以及线夹的挤压力时外层股线与线夹接触部位的应力分布情况。张秋桦[7]采用理论计算方法、有限元仿真方法以及试验测量方法，对张拉载荷下导线的应力及刚度进行研究。芮晓明等[8]提出了一种新型有效的建模分析方法，并利用Abaqus软件对所提出的方法进行研究。Raoof等[9]通过研究多层绞线的拉伸-扭转计算不同股线刚度的方法。Kumar等[10]忽略摩擦情况下研究多层电缆的轴向与弯曲响应，推导出了多层绞线拉伸和扭转刚度的表达式。Burks等[11]对铝导线复合芯M(ACCC)进行了数值研究，得到了导线在受热和载荷时的应力分布情况。Xiang等[12]提出了一种描述多股钢丝绳受轴向张力和轴向扭转响应的新模型，为钢绞线的疲劳和失效行为提供了新的见解。

国内外研究关于导线在张力作用下的导线分层应力分布较多，而在温度和张力共同作用下导线分层应力分布的研究较为缺乏。

本文通过理论推导得到钢芯铝绞线在温度和张力共同作用下，分层应力计算公式；以某实际工程为例，运用数值仿真方法，模拟分析了JL/G1A-400/35的各层股线的轴向应力并与理论结果进行对比分析。

1 温度和张力共同作用下分层应力理论

在张力和温度共同作用下，架空导线产生轴向伸长，为保证导线变形协调，做出以下3个假设：

(1) 导线在变形过程中满足平面假设，即各线股的轴心线在同一个圆截面内，同一层线股受力状态相同;

(2) 钢芯铝绞线在变形过程中始终处于弹性阶段;

(3) 忽略线股间的挤压和摩擦。

(a) 导线结构图 (b) 股线展开图 (c) 股线在温度和张力作用下变形图图1 股线在张力和温度共同作用下变形示意图Fig.1 Deformation diagram of strands under the joint action of tension and temperature

股线在张力和温度共同作用下变形示意图见图1。第n层股线中心线的参数方程为

(1)

式中：Rn为第n股层的半径；Rn=Dn-dn；Dn为第n层股线外径；dn为第n层股线直径；Pn为第n层股线节距；θn为第n层股线缠绕时该层圆上的圆心角。

由几何关系知：

(2)

式中：βn为捻角(扭角)，即线股沿内层芯线轴缠绕与轴线方向所称的夹角。

由股线参数方程知，第n层股线微弧长为

(3)

式(3)积分可得，第n层股线长度(弧长)为

(4)

对式(4)中Sn，Rn，Pn，θn微分有

(5)

由式(5)、式(4)可得

(6)

第n层股线轴向应变：

(7)

第n层股线径向应变为

(8)

由式(2)、式(6)、式(7)和式(8)联立可得：

(9)

第n层股线股向应变：

(10)

式中：βn为捻角(扭角)，即线股沿内层芯线轴缠绕与轴线方向所称的夹角；μn为第n层的股线的泊松比。

钢芯铝绞线导线在温度和张力作用下，导线轴向方向满足变形协调，即各股线具有相同的轴向伸长率：

(11)

式中：T为导线张力；E为导线综合弹性模量；A为导线截面面积；α为导线轴向综合热膨胀系数；ti为导线某一状态温度；t0为导线制造温度，一般取20 ℃。

综合弹性模量计算公式[13]：

(12)

式中：En为第n层的股线的弹性模量；βn为第n层线股扭角；An为第n层线股截面总面积。

导线的轴向综合温度线膨胀系数计算公式[13]：

(13)

式中：αn为第n层的股线的温度膨胀系数；En为第n层的股线弹性模量；An为第n层线股截面总面积。

温度只引起导线股向伸长，不产生温度应力，故导线仅在张力作用下各层股向应变为

(14)

第n层股线的股向应力为

(15)

第n层股线的轴向应力为

(16)

第n层导线轴向张力为

(17)

导线轴向总张力为

(18)

已知t1温度下导线的平均应力σ01，根据不等高悬点架空线状态方程[14]式(19)，得到t2温度下导线的平均应力σ02：

(19)

式中：σ01，σ02分别为两种状态下架空线弧垂最低点处的应力；γ1，γ2分别为两种状态下架空线的比载；t1，t2分别为两种状态下架空线的温度；l，β分别为该档的档距和高差角；α，E分别为架空线的轴向综合温度膨胀系数和综合弹性模量。

在t2温度下导线总张力为

(20)

取t1=20 ℃为导线制造温度，σ01为导线的年平均运行应力；同时将实际工程数据代入导线状态方程式(19)得到某一温度下导线张力T如式(20)，再根据式(11)得到导线轴向应变ε，代入式(14)得到张力作用下各层股向应变，再将各层股线股向应变代入式(16)和式(17)中得到导线各层股线轴向应力和张力。

2 导线建模及工程实例

2.1 导线几何模型及材料参数

选用导线型号为JL/G1A-400/35，钢芯的弹性模量为190 GPa，泊松比为0.3，热膨胀系数为11.5×10-6℃-1；铝股的弹性模量为55 GPa，泊松比为0.3，热膨胀系数为23×10-6℃-1；导线的几何参数见1。

表1 钢芯铝绞线JL/G1A-400/35几何建模参数Tab.1 Geometric parameters of steel-cored aluminum stranded wire JL/G1A-400/35

2.2 网格划分及边界条件

在Solid Works中完成导线JL/G1A-400/35的几何模型，导入到ANSYS中进行有限元分析。取导线长度为100 mm，并划分网格如图2所示。

图2 JL/G1A-400/35导线轴向网格划分及截面网格划分Fig.2 Axial mesh division and section mesh division of JL/G1A-400/35 conductor

边界条件：接触设置为绑定约束；约束导线端部x=0 mm截面上设置固定端，约束X、Y、Z3个方向上的全部自由度；仅考虑导线对称轴向(x方向)受拉，忽略重力影响。在导线另一端x=100 mm截面建立刚性域，保证x=100 mm截面上节点沿轴向位移相同；最后在x=100 mm截面上施加集中力。研究在张力作用下导线应力分层效应时，所加集中力为20%额定拉断力(RTS)。

2.3 工程实例

某不等高悬点的架空导线，档距为l=400 m，高差为h=50 m，选用导线型号为JL/G1A-400/35，导线的基本参数和力学指标如表2。

表2 JL/G1A-400/35导线各项参数表Tab.2 JL/G1A-400/35 wire parameters table

计算温度场中导线分层应力时，首先根据导线状态方程以20 ℃为年平均运行张力为起点，计算出各温度下导线张力如表3所示。

表3不同温度下导线张力值Tab.3 Conductor tension values at different temperatures

由表3可知：导线运行张力随着温度的升高而减小，随着温度的下降而增大。

3 计算结果及分析

3.1 仅在张力作用下钢芯铝绞线分层应力分布

由图3可知：钢芯铝绞线中钢芯层承担的应力明显大于铝股层，约为铝股的3～4倍；这符合钢芯铝绞线的实际工作情况：钢芯承担主要张力，铝股主要传输电能[13]。

图3 JL/G1A-400/35导线中间截面(x=50 mm)20%RTS下轴向应力云图Fig.3 Cloud diagram of axial stress under 20%RTS of JL/G1A-400/35 conductor middle section (x=50 mm)

在有限元仿真软件中提取导线各层轴向应力的平均值，与理论进行对比得到表4如下。

表4 JL/G1A-400/35导线在20%RTS下各层股线轴向应力有限元值与理论值Tab.4 Finite element and theoretical values of axial stress in each layer of JL/G1A-400/35 conductor under 20%RTS

由表4可知：钢芯铝绞线的分层应力有限元仿真值和理论值之间的误差在3%以内，满足工程实际要求，进一步说明了有限元仿真的正确性和准确性。钢芯铝绞线中钢芯层承担的应力明显大于铝股层，约为铝股的3～4倍；股线张力钢芯大于铝股，这符合钢芯铝绞线的实际工作情况。有限元仿真值和理论值之间的误差产生的原因为：理论推导忽略了摩擦挤压效应，有限元仿真考虑了挤压以及绞线的拉扭耦合效应。

3.2 钢芯铝绞线在温度场中分层应力分析

我国设计规范规定普通钢芯铝绞线的允许运行温度为-40 ℃到70 ℃之间[15]。故在实例分析时，取-40 ℃到70 ℃之间每隔10 ℃进行验算。通过理论计算和有限元分析结果如表5所示。

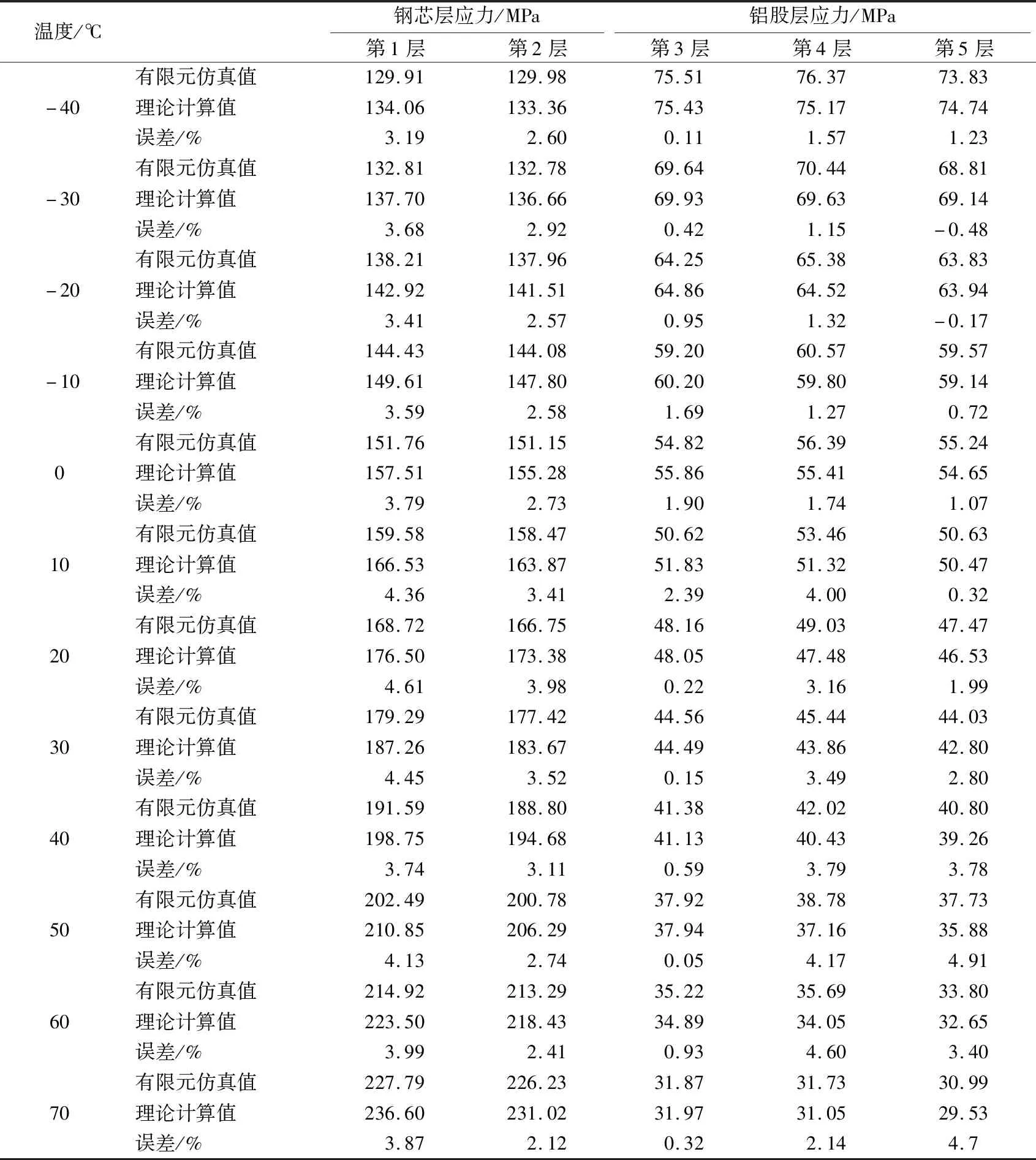
表5 JL/G1A-400/35股线在不同温度及对应张力下轴向分层应力表Tab.5 Axial delamination stress table of JL/G1A-400/35 strand at different temperatures and corresponding tensions

可知：不同温度下钢芯铝绞线的分层应力有限元仿真值和理论值之间的误差在5%以内，满足工程实际要求，进一步说明了有限元仿真的正确性和准确性。由图5可知，随着温度升高钢芯层应力在增大，铝股层应力在减小。产生上述现象的原因为：铝股的热膨胀系数约为钢芯的2倍，在温度作用下铝股膨胀的快，钢芯膨胀的慢，钢芯和铝股之间为保持变形协调，钢芯层施加给铝股层压力，而铝股层给钢芯层拉力；从而导致钢芯层的应力随着温度的上升而增加，铝股层应力随着温度的上升而减小。

4 结论

(1) 不同温度下钢芯铝绞线的分层应力有限元仿真值和理论值之间的误差在5%以内，满足工程实际要求，进一步说明了有限元仿真和理论推导的正确性和准确性。

(2) 在仅在张力作用下，钢芯铝绞线轴向应力会出现明显的分层效应。钢芯铝绞线中钢芯层承担的应力明显大于铝股层，约为铝股的3～4倍；股线张力钢芯大于铝股，符合钢芯铝绞线的实际工作情况。

(3) 在张力和温度共同作用下，导线运行张力随着温度的升高而减小；同时随着温度升高钢芯层应力在增大，铝股层应力在减小。当温度超过某一值(拐点温度)时，铝股将不受力，钢芯承担全部张力。