基于里兹法的输电铁塔塔脚板内力计算及其应用
肖奉英,杨垂玮,李响,张雷,黄模佳
(1.南昌大学工程力学系,江西 南昌 330031;2.中国能源建设集团安徽省电力设计院有限公司,安徽 合肥 230601)
近年来,随着电力需求的猛增,输电线路向高电压、大容量、多回路发展,铁塔承受的荷载持续增加[1-2],从而对塔脚板的承载力提出了更高的要求,直接导致了塔脚板的设计厚度越来越大。其中,较为常用的一种塔脚板为格构式方型塔脚板,该塔脚板主要由靴板与底板焊接而成,当塔脚板处于拉工况时,在拉力作用下,塔架上部结构所承受的荷载通过塔脚板的地脚螺栓传递给基础,在传递过程中,靴板与底板连接处的应力最大,故研究靴板与底板连接处的内力分布是设计塔脚板厚度的重要依据,塔脚板设计的安全性、可靠性和经济性[3]已经引起了输电线路工程设计人员的广泛重视。现行工程设计人员均是按照《架空输电线路杆塔结构设计技术规定》[4]给出的方法进行塔脚板的结构设计,由于现行规范[4]中给出的方法过于保守,从而导致塔脚板设计厚度过大的问题迟迟无法解决。因此,输电铁塔(尤其是特高压输电铁塔)塔脚板厚度的合理取值问题是电力工程中亟需解决的一个关键问题。
国内学者对于输电铁塔塔脚板的结构设计做了大量的研究工作。张小兵等[5]基于连续介质力学及有限变形理论,将板转换为壳元进行模拟计算,为塔脚板转换为壳元计算提供了理论依据。刘俊卿等[6]通过有限元模拟了塔脚板的应力分布情况,并结合“塑性分析,弹性设计”的思想,提出了一种基于屈服线理论的四地脚螺栓塔脚板抗拉承载力计算公式。殷黎明等[7]在现行规范[4]的计算分析基础上,以工程实际中的方形塔脚板为例,针对塔脚板不同支承形式的矩形区隔板进行仿真计算,根据仿真计算结果对现行规范[4]中的方形塔脚板底板厚度计算公式进行了修正。张丽娟等[8]利用ANSYS有限元软件对处于拉工况的加劲四地脚螺栓塔脚板进行了研究,并将有限元仿真计算结果与现行规范进行比较,发现现行规范的结果偏大,并根据有限元计算结果给出了塔脚板结构设计和材料选用的一些方法和建议供工程中参考使用。可以看出,国内学者主要从数值仿真和试验研究两个方面,结合现行规范中给出的设计方法,提出塔脚板厚度的修正表达式,但相对来讲,直接从板的理论上给出板的求解表达式,不仅相对简单可靠,而且可以更好地反映塔脚板内力分布的具体情况。
基于上述研究背景,本文将从理论上以无加劲的四地脚螺栓方型塔脚板为对象展开研究计算,考虑角钢所在的区隔块上靴板与底板连接处的应力最大,取塔脚板所含角钢的四分之一作为研究对象,将其转换为力学模型,假设靴板与底板连接处的两端为固定端,其余两端自由,螺栓处任意作用一个集中荷载,利用最小势能原理的里兹法[9]对该力学模型开展理论研究工作。首先通过里兹法建立符合塔脚板边界条件的位移函数w,并对该函数进行无量纲化,使其满足任意尺寸的塔脚板,同时利用Maple编程软件进行计算,从而给出四地脚螺栓塔脚板在拉工况下单位长度最大弯矩的理论表达式,并最终对该理论表达式进行简化,从而达到工程中可以采用的形式,并给出相应的厚度计算表达式为塔脚板厚度的合理设计提供参考依据。
1 无加劲方型塔脚板的现行规范
方型塔脚板主要分为无加劲塔脚板和有加劲塔脚板两种。本文主要研究无加劲方型塔脚板(图1),塔脚板的厚度主要取决于板底的最大弯矩,我国现行规范中,对于受拉工况的无加劲方型塔脚板,板底单位长度的弯矩计算方法如下:
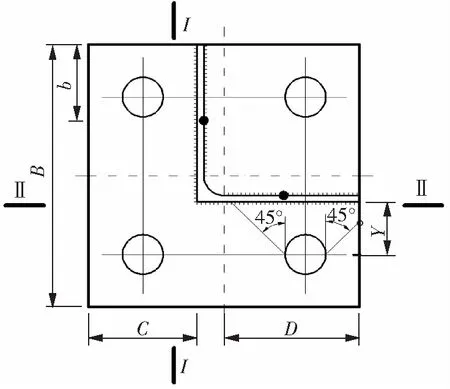
图1 无加劲方型塔脚板Fig.1 Square tower base without stiffener
(1)
式中:T为基础作用的上拔力;F为单个地脚螺栓承受的上拔力;Y为地脚螺栓中心至主角钢边的距离;D为地脚螺栓中心对应的Ⅱ-Ⅱ断面的计算宽度。
根据塔脚板的弯矩表达式,现行规范的塔脚板厚度计算表达式如下:
(2)
式中:t为塔脚板厚度;f为钢材的抗拉强度设计值。
式(1)表明,塔脚板现行规范中给出的塔脚板弯矩计算方法主要是基于以下假设得出的:受拉工况下,地脚螺栓均匀受力;假定角钢主材作为塔脚板的有效支承边,各区隔板均视为悬挑板。然而在实际工程中,塔脚板的应力场和位移场极为复杂,仅仅按照弹性假定理论进行简单的弯矩求解无法反映工程实际,且在前期已有的塔脚板有限元仿真计算基础上,其计算结果表明塔脚板设计规范弯矩值是有限元计算结果的两倍,用式(2)进行计算可以得到,塔脚板实际的厚度设计值要比规范设计值小将近30%,因此本文在现行规范的基础上提出新的假设,并基于里兹法给出塔脚板最大弯矩的合理表达式,并利用式(2)得到新的厚度设计表达式,使工程中能更加合理地设计塔脚板厚度。
2 塔脚板的弯矩解析解的推导
对于现行规范[4]中的给出的弯矩求解表达式,力学分析模型过于简单,无法贴近工程实际,工程中真实的塔脚板如图2所示,塔脚板通过连接螺栓与上部结构连接,当塔脚板处于拉工况时,上部结构受到的拉力通过连接螺栓传递给靴板,再通过靴板往下传递至与底板连接的地脚螺栓,地脚螺栓通过螺杆将荷载传递给基础。整个传递过程中,主要是通过4个地脚螺栓传递拉荷载,故计算时,地脚螺栓的位置可等同于在板上作用一个集中荷载。

图2 铁塔角钢塔脚板Fig.2 Tower angle steel tower foot plate
一般角钢所在的区隔板弯矩最大,故取该区隔块作为研究对象,假设该区隔板是一块两相邻边固定、两相邻边自由的板,靴板与底板连接的部分即为固定端,边长为a,对于拉工况作用下的塔脚板,主要是螺栓起作用,因此在螺栓的位置用载荷P取代螺栓,简化模型如图3所示。

图3 塔脚板简化计算模型Fig.3 Simplified calculation model of tower foot
基于上述假设,将塔脚板问题转换为矩形薄板求解问题,采用里兹法求解矩形薄板的弯曲问题,首先假设板受到的荷载为q(x,y),则矩形薄板的弯曲方程可表示为:
D∇2∇2w(x,y)=q(x,y)
(3)
其中:
(4)
式中:ν为泊松比;D为挠曲刚度;E为弹性模量;t为板的厚度。
对于两端固定、两端自由的塔脚板,其固定端的位移和转角为零,边界条件为:
(5)
(6)
采用一种利用边界条件求出位移函数的方法,即里兹法。里兹法是基于最小势能原理得到位移w的一种近似方法,可以将位移函数w表示为:
w=a1φ1(x,y)+a2φ2(x,y)+…+anφn(x,y)
(7)
位移函数中φ1(x,y),φ2(x,y),…,φn(x,y)均为已知函数,满足板的位移边界条件,a1,a2,…,an都是待定常数。利用式(5)~式(7)建立含10个系数的位移方程可得:
w=x2y2(a1+a2x+a3y+a4x2+a5xy+a6y2+a7x3+a8x2y+a9xy2+a10y3)
(8)
这里采用了10个函数去计算近似位移,其中:
φ1(x,y)=x2y2,φ2(x,y)=x3y2,…,φ10(x,y)=y5
(9)
上式中任一函数均满足塔脚板的边界条件,为了使该方程适用于任何尺寸的方型塔脚板,所以要对x、y进行无量纲化,同时,将位移方程用含矩阵变量的方式表示出来:
w=ahTb
(10)
式中:
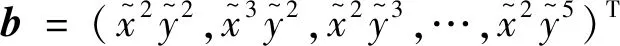
(11)

当塔脚板受到外力作用时,板对于整个系统的形变势能为:
U=U1-V
(12)
受拉时,主要靠螺栓锚杆处受力,将螺栓锚杆处假设成一个加载点(x1,y1),且受到的集中荷载为P,则:
U1=∬udxdy,V=Pw(x1,y1)
(13)
其中:
(14)
式中:U1表示板的变形能;V为集中荷载P作用的外力势能;U为系统的总势能。
根据最小势能原理,板的真实位移w应使U取极值,w应使得U的一阶变分等于零,则有:
δU=0
(15)
利用式(15)对ai依次进行求导,引出A、H矩阵,这里引出A、H矩阵,主要是为了求出h矩阵,进而得到h的转置矩阵,具体计算步骤如下:
(16)

(17)
且A、H矩阵满足:
h=A-1H
(18)
式(10)只有b矩阵里面含变量,求弯矩M1只对b矩阵求导:
(19)
薄板的内力可以用挠度函数表示为:
桐庐县2018年“7.27”廊桥桥顶垮塌突发事件气象服务与应急处置浅析 陈斌 詹平华 江涛 张燕艳 江敏超(4∶17)
(20)
(21)

3 弯矩解析解的数值验证
为了验证式(21)的可靠性,利用ABAQUS软件进行有限元仿真模拟计算。由于塔脚板的厚度与边宽的比值小于1/8,所以塔脚板属于薄板,主要采用STRI65即六节点三角形薄壳网格单元计算,同时也用C3D20R即二十节点二次六面体网格单元进行辅助验证。本次共建了8个有限元模型,模型可分为两大类:第1类是塔脚板简化模型,该模型仅为塔脚板的1/4,即假设是两端固定、两端自由的板;第2类是塔脚板原模型,该模型与工程中的塔脚板一致。有限元模型网格划分如图4所示。

图4 塔脚板网格划分模型Fig.4 Tower foot plate meshing model
塔脚板和靴板在装配过程中用合并实例命令将两个部件变为一个整体,角钢与靴板设定为绑定连接,螺栓处的表现形式为在塔脚板上约束4个点即为螺栓的位置,采用的约束方式是完全固定。第1类模型采用STRI65和C3D20R两种网格单元进行计算,上拔力T直接加在螺栓的位置;第2类模型只采用STRI65网格单元进行计算,上拔力T施加在角钢主材上。假定材料是理想弹性材料,钢的弹性模量取E=206 kN·mm-2,泊松比取ν=0.3。
计算过程中,通过改变螺栓的布置位置,力的大小以及板厚等变量,对有限元模型进行计算,从而验证理论值是否接近有限元值,并找出规范值与有限元值之间的差距。通过对8个有限元模型进行计算,可以得出一系列的有限元计算结果,其中塔脚板的Mises应力云图分布如图5~图7所示。
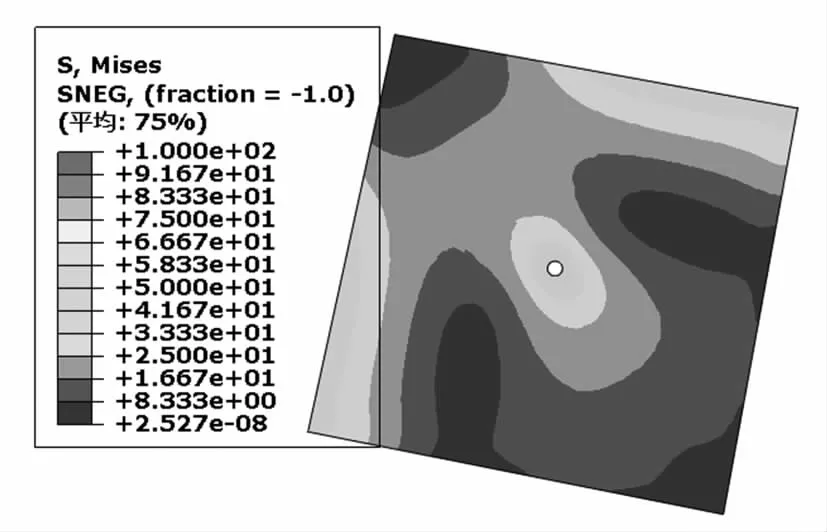
图5 简化壳元四地脚螺栓塔脚板Fig.5 Simplified shell element four anchor bolt tower foot plate

图6 简化20节点单元四地脚螺栓塔脚板Fig.6 Simplified 20-node element four anchor bolt tower foot plate

图7 壳元四地脚螺栓塔脚板Fig.7 Shell element four anchor bolt tower foot plate
由图5、图6可以得到,用STRI65单元和C3D20R单元计算出来的塔脚板应力值和应力分布很接近,证明塔脚板除了可以用壳元计算之外,还可以采用三维实体C3D20R单元计算,尤其是需要设置螺栓与塔脚板的连接时,采用三维实体能更好地设置接触关系。由图5、图7可以得到,简化的塔脚板和原模型塔脚板的应力分布和位移趋势一样,说明将塔脚板简化成两端固定、两端自由的板和螺栓处视为作用一个集中力P符合实际情况。
由表1可以看出,用里兹法计算出来的数值接近有限元值,进一步印证了式(21)的可靠性。对于四地脚螺栓塔脚板来说,通过与规范值的比对,能量法计算的理论值和有限元值比规范值都要小,规范值大约是有限元值的两倍,而设计的理论值不仅比规范值小很多,与有限元值也比较接近,因而也相对安全可靠;由模型3~模型5的计算结果可得,弯矩值与上拔力T成正比,对于4地脚螺栓塔脚板来说,通过提取支反力RF3所得到的P可知,4个地脚螺栓承受的拉力实际上不对称,而最大的应力则发生在区隔板面积最大的那一块;由模型5、7、8的有限元值可以得出,在塔脚板厚度、上拔力一样的情况下,螺栓布置越靠近板端,弯矩值就越大,越靠近角钢,弯矩值就越小,可见力的传递距离变小时,弯矩也会减小;对于模型3、6的有限元计算结果,在厚度不一样其他条件一样的情况下,应力值不一样,板越薄,应力值越大,但弯矩值比较接近。
得到弯矩大小之后,塔脚板也应满足强度条件,强度校核由以下表达式确定
(22)
式中:W为塔脚板的单位抗弯模量;M1为靴板与塔脚板连接处的最大单位长度弯矩;f为钢材的抗拉强度设计值,同样的,如果已知力的大小,可通过式(22)反推塔脚板的厚度。
4 试验数据对比
为了进一步有效验证本文提出的弯矩表达式的可靠性,借助于我们课题组曾经做过的塔脚板节点承载力真型试验结果,从试验研究的角度进行验证。
图8所示为四地脚螺栓塔脚板应变花的粘贴位置标示图,图9所示为塔脚板节点承载力真型试验加载图,整个试验过程中,塔脚板应变片布置位置是根据前期有限元仿真计算得出的应变较大处[10-12],在塔脚板上共布置13个应变花,每个应变花有3个应变,共39个测点,加载工况为拉工况。
试验的应变花位置主要是布置在靴板与塔脚板的连接处附近的位置,该试验所得到的数据正好是我们所需要的数值。该塔脚板的主区隔尺寸为400 mm×400 mm,螺栓布置在距离靴板200 mm的位置,每一个螺栓承受的上拔力为100 kN。经分析,试验所得的单位长度弯矩值为25.357 kN,用式(21)计算得出的单位长度弯矩值为26.300 kN,用式(1)计算得出的规范值为50.0 kN。由此可见,试验所得的数值与解析解比较接近,进一步验证了本文假设的力学模型与真实的塔脚板模型相吻合。其次,规范值是试验值的两倍,可见按照现行规范给出的方法进行塔脚板的厚度设计显然过于保守,不经济。

(a) 塔脚板试验模型
5 结论
1) 在理论研究方面,基于里兹法,给出了四地脚螺栓塔脚板在拉工况作用下塔脚板的最大单位长度弯矩的解析解;在数值研究方面,利用有限元软件ABAQUS建立了8个塔脚板求解,将有限元结果与本文提出的塔脚板弯矩求解结果进行了对比,二者结果吻合较好;在试验研究方面,借助于塔脚板承载力真型试验的结果,进一步验证了本文给出的弯矩表达式的可靠性。
2) 基于里兹法推导出来的弯矩表达式表明,单位长度弯矩的大小与塔脚板的厚度无关,但是塔脚板的极限承载力与板厚息息相关;因此,为了满足承载力的要求,建议在实际工程中,在满足构造条件的前提下,塔脚板尽量做小一点且厚一点。
3) 有限元对比分析结果表明,按照现行行业规范的方法求解出的弯矩值将近是有限元值的两倍;相比之下,通过里兹法计算出来的表达式得到的弯矩值要小很多,很大程度上可以降低塔脚板的厚度设计值,节省材料30%左右,还可以保证材料性能的充分发挥。
4)对于复杂的方程,可以采用最小二乘法、多项式拟合等拟合方法将复杂的方程简化成简单的方程,从而使计算变得简单方便,便于指导实际工程应用,为今后类似问题的求解提供借鉴。

