考虑负荷波动与电压偏移的城市充电桩分类优化配置

曹佳佳，王淳，霍崇辉，陶多才，罗晨煜，吴潇翔

(南昌大学能源与电气工程系，江西 南昌 330031)

随着化石能源的逐渐枯竭与环境污染的日益加剧，世界各国对发展以电动汽车(electric vehicle,EV)为代表的清洁能源交通工具给予了足够重视，具有绿色、高效特点的EV将成为未来汽车行业的最新发展方向[1-2]。充电桩的不合理配置会对电网运行的经济性、稳定性以及用户充电的方便可靠性等带来严重影响[3]。

近年来，国内外学者对EV充电设施优化选址定容问题进行了深入研究。在EV充电站的优化规划方面，文献[4]将充电设施分类，考虑不同充电设施间的相互影响，基于改进的P中心定位模型建立了一个以总投资成本、运维成本、电量成本和充电站用户成本最小为目标的整数线性规划模型。文献[5]以充电站投资收益为上层目标函数，以充电用户满意度为下层目标函数，建立了一种考虑充电站投资收益和充电用户效用耦合决策的EV充电站双层优化模型。文献[6]提出了计及全寿命周期成本的两阶段EV充电网络规划模型。文献[7-8]分别以充电站投资运行成本和用户成本之和最小化为目标函数，建立充电站选址定容模型。文献[9]提出了基于用户利益的充电设施优化规划方案。文献[10]提出利用多通道损失制排队论模型对充电站的充电桩数目进行配置。文献[11]构建了以电站投资运营者与汽车用户双方综合效益最大为目标的高速公路充电站优化规划模型。文献[12-14]分别对分布式电源与充电站联合选址定容问题进行了研究。文献[15-16]在对充电站进行规划同时，考虑了分布式电源的配置和配电网的扩展规划。在EV充电桩选址定容方面，文献[17]以整个电动出租车充电站服务系统的总费用最低为目标函数，建立了电动出租车充电桩的优化配置模型。文献[18]从计及EV分布不平衡的充电需求确定、考虑充电距离最小的公共充电桩位置规划和计及EV多日一充的充电桩容量确定三方面依次对社会公共充电桩规划进行分析。

综上所述，现有EV充电设施规划文献大多数是对充电站选址定容问题进行研究，对城市充电桩数量确定和容量分配进行研究的文献很少。本文考虑不同区域用户的充电行为对充电桩进行分类，提出一种考虑负荷波动和电压偏移的城市充电桩分类优化配置方法，采用遗传算法求解，并通过算例分析，验证了所提方法可以合理选择出对配电网影响较小的充电桩优化配置方案。

1 充电桩分类

目前我国电动汽车充电桩按充电方式主要分为交流充电桩和直流充电桩。根据GB/T 20234.2—2015《电动汽车传导充电用连接装置 第2部分：交流充电接口》和GB/T 20234.3—2015《电动汽车传导充电用连接装置 第3部分：直流充电接口》的规定，我国充电桩充电模式如表1所示[4]。

根据用途不同，城市EV主要分为公交车、私家车、出租车和公务车4种类型。停车场所对充电桩的建设有一定的影响，由于公交车停车点较集中，可直接在公交专用停车场内建设相配套的充电桩来进行充电，不需要进行充电桩规划[4]。本文仅考虑私家车、出租车和公务车的充电需求来进行充电桩优化配置。

由于充电行为直接影响到EV的电池寿命，根据充电时间是否充足，不同停车点的EV用户的充电行为不同。停车点在办公区时，停车时间相对充足，EV用户通常会选择交流常规充电桩来进行充电。停车点在商业区时，停车时间比较短，电动汽车用户通常会选择直流快速充电桩来进行充电。停车点在居民区时，停车时间比较充足，多数用户会安装私人充电桩,如交流慢速充电桩来充电，此外，部分居民区停车用户没有安装私人充电桩，则会选择附近公共直流快速充电桩进行快速充电。

城市充电桩建设时，应根据不同区域停车点EV用户的充电行为来选择该停车点需要建设的充电桩类型。本文根据不同区域停车点用户的充电行为特点，将充电桩分为4类：建设在居民区的慢速私人充电桩(L1)、建设在居民区的快速公共充电桩(Lr3)、建设在商业区的快速公共充电桩(Lc3)和建设在办公区的常规公共充电桩(L2)。

2 优化规划模型

2.1 充电需求

1) EV日行驶距离不确定性。

EV用户的出行在时间和空间上都具有随机性。根据NHTS统计分析，电动出租车日行驶距离满足正态分布[5]，如式(1)所示:

(1)

式中：μ1和σ1分别为电动出租车的日行驶距离期望和标准差。μ1=155.02；σ1=41.53[5]。

私家车和公务车的日行驶距离满足对数正态分布[6]，如式(2)所示。

(2)

式中：μ2和σ2分别为电动私家车、公务车的的日行驶距离期望和标准差。μ2=3.2；σ2=0.88[6]。

2) 不同类型EV日充电需求。

充电桩配置首先需要满足各种类型EV的充电需求。由EV的日行驶距离概率密度函数，采用Monte Carlo抽样得到EV的日总行驶距离。EV的日充电需求如式(3)所示。

(3)

式中：EV类型集合B={私家车,出租车,公务车}；Wb为类型为b的EV日总充电需求；Lb为类型为b的EV的日总行驶距离；Sb为b类型EV的百公里耗电量。

3) 不同类型充电桩的日总充电需求。

根据私家车、出租车和公务车在不同类型充电桩的充电需求比例，将私家车、出租车和公务车的充电需求分配到4种类型充电桩上，如式(4)所示。

(4)

式中：a为充电桩类型；A为充电桩类型集合，A={L1,L2,Lr3,Lc3}；Qa为a类型充电桩的日总充电需求；λab为b类型EV在a类型充电桩的充电需求比例。

2.2 充电桩数量确定

EV到达公共充电桩进行充电的过程符合排队论模型。排队论中顾客的排队方式有等待制、损失制和混合制。通常用户在商业区逗留时间较短，当用户到达充电桩时，若所有充电桩都被占用，则会选择直接离去，排队方式属于损失制(M/M/S/S)。在居民区和办公区，当用户到达充电桩时，若所有充电桩都被占用，一般会进入排队状态，排队方式属于等待制(M/M/S)。

假设用户一定时间到达充电桩的过程满足泊松分布，强度为λ；充电桩的数量为n，充电桩之间互相独立[10]。用户在每个充电桩的充电时间服从参数为μ的负指数分布，1/μ即为用户的充电时长。

根据排队论中关于损失制排队系统的相关理论，可得系统损失概率如式(5)所示[10]。

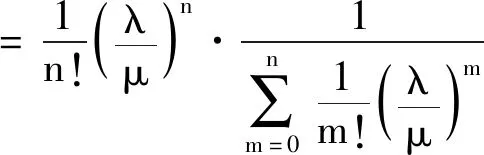
(5)

一个良好的充电服务系统，要保证绝大部分用户可以充电，即需要保证较低的系统损失概率[10]。建立以系统损失概率和充电需求为约束的商业区充电桩数量模型如式(6)所示。

(6)

式中：P损max为最大系统损失概率，设置为0.05[10]；PC、PT、PCmax分别为商业区最大充电负荷、充电桩总功率和充电桩功率上限；Z为正整数集合。

根据等待制排队系统的相关理论，充电桩全部空闲的概率如式(7)所示[2]。

(7)

式中：ρ=λ/nμ表示系统服务强度。

等待制排队模型的两个重要数量指标如式(8)所示[7]。

(8)

式中：Lq为平均排队长度；Wq为用户排队平均等待时间；以用户平均排队时间和充电需求为约束的居民区和办公区充电桩数量模型如式(9)所示。

(9)

式中：ni为充电桩类型为i的充电桩数量；Wq max为充电桩服务系统的最大用户排队平均等待时间，设置为0.16 h；PDi、PEi、PDimax分别为类型为i的充电桩服务系统的充电需求、充电桩总功率和充电桩功率上限。

平均每小时到达充电车辆数即为λ，根据各类型充电桩1 d内集中充电的5个时段内电动汽车的数量，λ取值可由式(10)取得。

(10)

式中：ceil为向上取整函数；λa为a类型充电桩平均每小时到达车辆数；Nat为a类型充电桩第t时刻服务车辆数，可根据t时刻a类型充电桩的总充电功率和a类型充电桩单位容量估计得到。

2.3 充电桩容量分配模型

城市充电桩基本都是建设在各区域的停车点，所以只需确定各区域充电桩的待建数量，然后根据建设考虑的因素将充电桩分配到各待建停车点即可。建立以配电网网损均值最小，负荷波动率均值最小和电压偏移之和最小的充电桩容量分配模型，如式(11)所示。

F=αminfloss+βminfload+γminfVdiff

(11)

式中：α、β、γ分别为网损均值floss、负荷波动率均值fload、电压偏移之和fVdiff的权重系数，总和为1。

将各时段网损求和再除以时段总数得到网损均值，如式(12)所示。

(12)

式中：t为时段，T为时段总数；l为配电系统支路集合；Iij(t)为节点i、j之间的电流；Rij为节点i、j之间的电阻。

负荷的标准差与负荷的均值之比为负荷波动率，表示单位平均负荷时的负荷分散程度。当负荷分散程度越大，标准差越大，负荷波动率也越大，即负荷波动性越大。负荷波动率均值如式(13)所示。

(13)

将系统所有节点电压偏移求和如式(14)所示。

(14)

式中：ft为t时刻所有节点的电压偏移总和；Vi为节点i的电压幅值；V0为平衡节点电压。

节点电压偏移之和定义如式(15)所示。

fVdiff=max(ft1,ft2,ft3,…,ftT)

(15)

式中：ft1，ft2，ft3，…，ftT分别为T个时段中每个时段的所有节点电压偏移总和。

配电网系统潮流约束和节点电压及支路功率约束如式(16)～式(19)所示。

(16)

(17)

Vmin≤Vi≤Vmax，i∈N

(18)

SL≤SLmax，L∈l

(19)

式中：Pi、Qi分别为节点i的注入有功功率和无功功率；Vi、Vj分别为节点i、j的电压值；Gij和Bij分别为支路i、j之间的电导和电纳；θ为节点i、j之间的相角差；Vi为节点i的电压；Vmin、Vmax分别为节点的电压上下限；SL为第L条线路的传输功率；SLmax为第L条线路传输功率的上限；l为线路集合。

2.4 评价指标

1) 经济性指标。

充电桩建设经济性包括充电桩的投资建设成本、土地成本和运维成本。运维成本按照初期投资成本百分比计算。

(20)

式中：Cec为充电桩年均投资建设成本；r0为回收率；t0为运行年限；η为运维成本所占比例；na为a类型充电桩的数量；pa为a类型充电桩的单价；S为单个充电桩的平均占地面积；Cg为区域类型为g的土地价格，g∈(居民区，商业区，办公区)。

2) 用户满意度指标。

在城市出行环境中，时间通常比较紧迫，考虑用户充电所消耗的时间成本和充电成本，建立用户满意度指标如式(21)所示。

(21)

式中：a表示充电桩类型；Causer为用户满意度指标，即用户出行日均成本；Ka为EV充电时长；Na为每天服务的EV数量；Rt为用户时间成本；Wqa为EV的排队时长；Qa为日总充电需求；Rg为区域类型为g的充电电价。

3 模型求解

3.1 遗传算法简介

遗传算法优化求解原理源自于自然遗传学和计算机科学，采用遗传算法求解实际问题时，首先需要将实际问题进行编码，形成便于计算机计算的具体的或者有固定结构字符串，称为染色体。染色体中字符的总个数成为染色体长度，染色体中由一个字符或者几个字符组成的基本信息单位称为基因。为了便于计算，一般情况下，染色体由0和1组成。适应函数是用来衡量染色体优劣的重要指标，其决定着种群进化的方向，可在优化目标的基础上确定，一般适应函数为能反映实际问题的目标函数。

借鉴于生物进化现象，遗传算法的遗传操作包括生殖、交叉和变异。

1) 生殖：根据适应度函数进行选择操作，适应度较大，即适应能力较强的染色体有较大的概率被选中并被保留，被选择保留的较为优化的染色体可进行后续遗传操作。

2) 交叉：将交叉算子作用于选择操作保留的染色体群，选取两个染色体，再根据给定的交叉率确定是否进行交叉操作。两点交叉是指在个体编码串中随机设置了两个交叉点，然后再进行部分基因交换。

3) 变异：根据给定的变异率确定是否进行变异，基本变异算子是指对群体中的个体码串随机挑选一个或多个基因座并对这些基因座的基因值以变异率做变动。

使用遗传算法求解，定义每个染色体基因对应为充电桩待建停车点的配电系统节点号，基因值为[0,m]之间的随机整数，m值可根据待建设点充电桩数量上限确定。假设某规划区待建点10个，每个待建设点充电桩数量上限为10，则该规划区的染色体长度为10，基因值为[0,10]之间的随机整数，如染色体[0 1 5 8 7 4 5 3 10 9]，基因值为0表示对应节点不建设充电桩，否则基因值即为对应节点建设充电桩的数量。

3.2 模型求解流程

分散式充电桩优化规划求解流程图如图1所示。详细步骤如下所示：

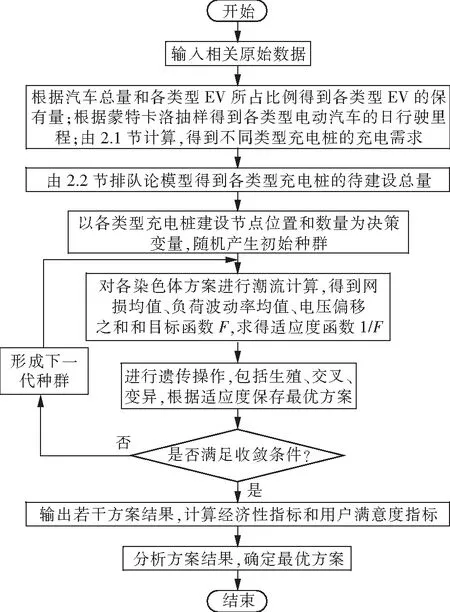
图1 模型求解流程图Fig.1 Flow chart of model solution

步骤1收集相关原始数据，根据汽车总量和各类型电动汽车所占比例计算各类型电动汽车保有量。

步骤2根据蒙特卡洛抽样得到各类型电动汽车的日行驶距离，由公式(3)得到各类型电动汽车的总的日充电需求。根据公式(4)计算不同类型充电桩的日总充电需求。

步骤3计算损失制充电桩排队论模型得到商业区待建设充电桩总数量；计算等待制充电桩排队论模型分别得出居民区、工业区的待建设充电桩总数量。

步骤4随机生成遗传算法初始种群。适应度函数计算：对种群中每个染色体方案进行潮流计算，得到各染色体的网损均值、负荷波动率均值、电压偏移之和和目标函数F，即得到适应度函数1/F。

步骤5进行遗传操作，包括生殖、交叉、变异，其中交叉率、变异率分别设置为0.8、0.1。生殖操作根据适应度进行选择操作。交叉操作：在相互配对的两个个体编码串中随机设置两个交叉点；交换两个个体在所设定的两个交叉点之间的部分染色体。变异操作：在染色体中随机挑选两个基因并对这些基因的基因值在约束内做变动。

步骤6根据适应度保存优良染色体，计算收敛条件和迭代次数。判断是否满足收敛条件或达到最大迭代次数，若是，输出保存的优良染色体，否则返回步骤5。

步骤7计算经济性指标和用户满意度指标，评价保存的优良方案，分析并确定最优方案。

4 算例分析

4.1 算例概况

以某城市开发区为例，规划年限为10年，将规划区分为居民区、商业区和办公区，如图2所示。假设汽车总量约为2万辆，其中电动公务车、电动出租车和电动私家车所占比例分别为0.48%、0.82%和4.0%[5]。假设EV百公里耗电量均为15 kW·h[6]。采用IEEE33节点测试系统，系统节点分布如图2所示，蓝色数字为节点号，蓝色实线为配电线路。

系统电压等级为12.66 kV，总有功负荷及无功负荷分别为3 715 kW、2 300 kVar。进行潮流计算时，将规划典型日等分为24个时段，每时段的长度均为1 h。充电负荷与基础负荷如图3、图4所示[19-20]。

各类型EV在不同类型充电桩上的充电需求比例如表2所示[4]。

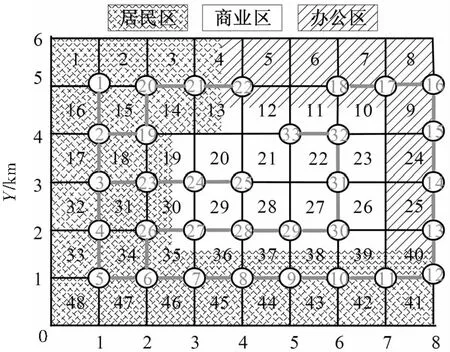
X/km图2 规划区示意图Fig.2 Graph of the planning area

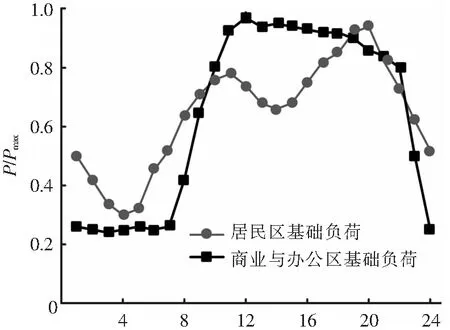
t/h图3 基础负荷曲线Fig.3 Load curve of charging load

t/h图4 充电负荷曲线Fig.4 Load curve of charging load

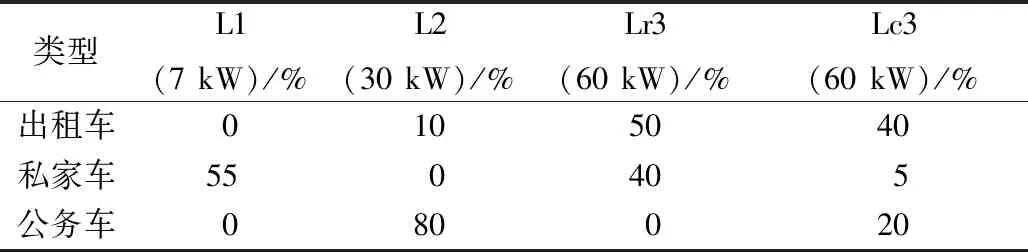
表2 充电需求分配比例Tab.2 Classification proportion of charging demands

不同区域土地价格[3]和充电价格如表3所示。

表3 各用地类型土地价格和充电价格Tab.3 Costs of different land and charging

模型中其他参数设置如表4所示。

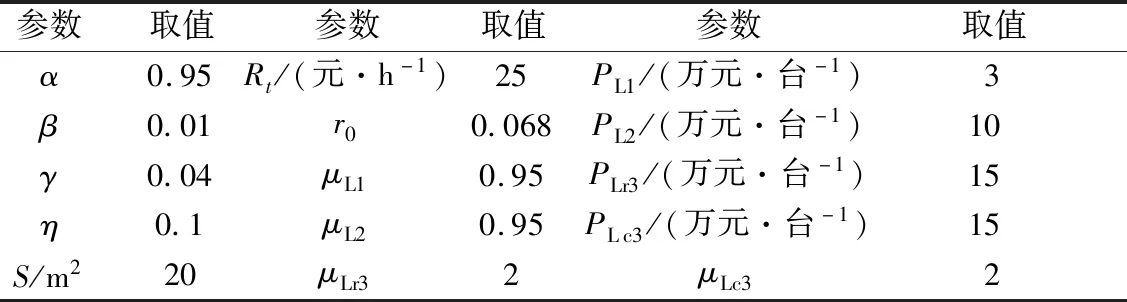
表4 模型参数设置Tab.4 Model parameter setting

4.2 结果分析

各类型充电桩的数量，充电时长和排队时长，如表5所示。

假设系统节点2到节点33附近均建有停车点，居民区快速充电停车点为3、5、7、10、20节点，其他充电桩可在规划区内各区相对应停车点建设。根据遗传算法，对各染色体方案进行潮流计算，得到各方案的网损均值、负荷波动率均值和电压偏移之和，然后求得各染色体方案的目标表函数F，根据适应度函数1/F保存4个优良方案，如表6所示。

从表6可以明显看出，方案1的负荷波动率为4个方案中最小，节点电压偏移之和在4个方案中仅比方案2大0.006，网损均值在4个方案中比方案2大0.8，但方案1的F值为4个方案中最小，因此方案1为4个方案中最优者。求解2.4节评价模型得到最优方案详情如表7所示。

表7 最优配置方案详情Tab.7 Results of optimal planning

5 结论

城市充电桩优化配置对EV的推广和配电系统的安全稳定具有至关重要的作用，合理地将充电桩进行分类建设有利于节省社会资源，提高设备利用率和提升用户满意度。本文考虑负荷波动和电压偏移对城市充电桩进行分类优化配置，得到以下结论：

1) 根据不同停车点EV用户的充电方式要求不同，将城市充电桩进行分类，可以更好地满足用户的充电需求。

2) 根据不同停车点EV用户的排队方式不同，采用不同的排队论来建立各类型充电桩的数量模型，能够更准确地得到各类型充电桩的最优数量。

3) 建立以配电网网损均值最小，负荷波动率均值最小和电压偏移之和最大者最小的目标函数，可以选择出对配电网影响较小的充电桩建设方案。