面向最大使用效益的充电站网络优化方法

孟祥福，杨 玉，张永库，张霄雁，陈柔冰，王 泽

辽宁工程技术大学 电子与信息工程学院，辽宁 葫芦岛125105

我国政府投入了大量资金建成了一定规模的充电站，目前完善充电基础设施体系是大规模运行电动汽车（electric vehicle，EV）的关键。根据2018 年中国电动汽车百人论坛发布的数据可知，我国的公共充电设施利用率不足15%，存在着大量闲置且冗余的充电站，局部地区充电站还发生了整体缺桩现象。目前，在充电站网络优化过程中一个不可缺少且研究不足的问题就是充电站的利用率不足和充电站的冗余问题。

以往大部分的研究工作集中在充电站选址优化过程，并未对现有的充电站布局合理性进行分析，忽略了电动汽车充电高峰期导致的充电站溢出问题、冗余充电站和充电站拥堵问题。如果不考虑现实充电站网络而直接对充电站进行优化，重新建设新的充电站网络，不仅需要大量的人力、物力，而且还会造成资源的浪费，不符合可持续发展的理念。另外，随着电动汽车渗透率迅速增长，电动汽车的需求分布也会随之发生变化，在充电站布局方面还应避免现实充电站间的无序竞争。针对以上问题，本文综合考虑了电动汽车充电高峰时期的溢出问题、充电站间的竞争、政府要求和电动汽车充电行为等多重因素对现实充电站网络优化的影响。利用广泛的传感数据感知电动汽车的充电行为，分析电动汽车充电行为规律。并且，分别为不同充电站单独建立队列系统，估计不同充电站的电动汽车到达率，分析电动汽车在不同充电站间的活跃程度，以识别城市充电热点。此外，基于全面挖掘电动汽车的充电行为特性、充电站之间竞争关系以及充电站的地理特征的相互作用，提出了一种新的方法来计算不同充电站之间在网络中的使用效益情况。最后，建立了充电站使用效益最大化优化模型，求解最佳充电站网络布局。

1 相关工作

针对电动汽车充电站选址优化问题，已经有许多学者对其进行了不同角度的研究。从电动汽车的充电需求出发，文献[2]提出了一个多类型纯电动汽车（battery electric vehicles，BEV）充电设施定位模型，以最小化公共社会成本为目标，满足不同类型BEV 的充电需求。Tu 等对电动出租车需求、电动出租车和充电站之间的交互进行建模，提出了一种时空需求覆盖方法，实现了电动出租车服务水平与充电服务之间的高质量权衡。为了优化充电站，一些研究也开始关注充电站的位置和大小。Ma 等建立了BASS 模型来预测不同年份电动汽车充电站的渗透率和数量。并根据排队理论，提出了电动汽车充电站选址优化模型，使电动汽车充电站的总成本最小，并采用枚举法求解该模型。为了提高充电站利用率，节约投资成本，Zhang 等提出了一种新充电点模型，即单输出多电缆充电点（single output multiple cables charging spots）。Bao 等针对交通网络拥挤的情况，提出了一种新的充电站定位问题，在有限的建设预算下，找到一组最优的充电站，使所有车辆都能通过沿途一个或多个充电站充电完成行程，最小化网络上的总旅行成本。文献[9]对电动汽车用户充电的搜索行为、导航行为和充电使用模式进行了分析和建模，提出了一种基于贝叶斯推理的充电需求评估方法。Luo 等研究了出行方式、电动汽车驾驶员行为、城市路网、电网与充电站布局之间的相互作用，提出了不同电动汽车渗透率下的多级充电站布局方法。葛少云等针对现有研究没有考虑车辆空间和时间变化的出行需求问题，提出了一种基于动态交通模拟的高速公路网电动汽车充电站优化规划技术。本文以武汉市中心区域的充电站网络为例，构建电动汽车队列系统，建立充电站最大使用效益模型，通过诊断并消除冗余充电站进行网络优化，同时识别网络中充电站拥堵区域，发现布局漏洞，为政府进一步的充电站规划提供有效建议。

2 电动汽车充电行为分析

2.1 影响充电站网络布局因素分析

（1）电动汽车充电行为规律

由于电动汽车的动力和续航能力较为中庸，在较长出行旅程中需反复多次进行充电。单个电动汽车充电行为在时空分布上具有较大的随机性，但是大规模电动汽车群的充电行为表现出了一定的规律性。通过对大型电动汽车群的充电行为进行分析，可以了解电动汽车在各个充电站间的活跃程度和移动方向。并且，基于以上分析，能够准确识别出电动汽车充电热点，挖掘电动汽车在城市充电站间的充电移动模式（如星形移动模式），有助于制定更好的充电站网络优化方案。电动汽车的空间充电热点，能够在很大程度上揭示城市电动汽车用户的充电偏好规律。通常，充电站需覆盖热点地区，特别是在人口稠密和交通需求相对较大的地区，然而供需之间不可避免地会存在大量矛盾。特别是在面临充电高峰时段的电动汽车充电需求量时，需尽可能使充电站网络布局与电动汽车充电需求分布一致，即布局与电动汽车充电偏好一致，最大限度地满足电动汽车的充电需求。电动汽车的移动模式则反映出了车流量的流动方式，为后续的优化扩展提供方向指导。

（2）充电站之间的关系

在电动汽车使用过程中，里程焦虑不可避免，它反映出司机对电动汽车是否有足够的电量到达目的地的一种担心。一旦电动汽车荷电状态处于较低水平，电动汽车用户将会选择在可接受充电距离范围D内的充电站进行充电。假设此时电动汽车与充电站间的距离为(→)，与充电站的距离为(→)，若式（1）与式（2）同时成立，则充电站与将会产生竞争关系。

虽然竞争力较强的充电站会吸引更多的电动汽车用户访问，但是一旦大部分用户选择同一时间段前往同一充电站充电（高峰期），将会导致充电站的溢出，电动汽车充电等待时间将直线上升。这种情况下，通常需要借助附近的充电站来缓解本地充电压力，从而形成充电站间依赖关系。由此可知，充电站间能够相互影响彼此。因此，在充电站网络优化过程中，充电站间的关系是网络优化过程中必须考虑的一个重要因素，无论是关闭还是新增充电站都将会对网络中其他充电站产生影响，同时还关系到电动汽车的用户体验。

（3）政府规划部门要求

图1 显示了武汉市中心地区一些充电站的局部视图。站点的大小表示电动汽车的平均到达率。从图1（a）可以看出，该区域内充电站分布非常密集，存在冗余充电站（绿色）。因此，政府可以考虑关闭其中的一些站点，以减少公共资源的浪费。相反，从图1（b）可知，大量电动汽车频繁访问该区域内的充电站，因此这些充电站的充电等待时间往往较长（红色），造成一定程度的充电站拥堵。政府可以考虑在附近新增一些充电站来缓解区域内的充电压力。这些现象显然反映了目前武汉市充电站网络布局并不合理。由此可见，需要设计一个基于真实充电站网络的交互式优化系统，用户可以根据实际需求设置不同的调优参数，从而诊断和消除网络中的冗余充电站获取最佳充电站网络方案，提高充电站利用率，同时识别网络中产生充电站拥堵（供不应求）的区域发现布局漏洞。

图1 充电站局部视图Fig.1 Local view of charging stations

2.2 电动汽车充电特性

在电动汽车用户选择充电服务过程中，考虑到首次抵达的充电站有可能发生溢出，因此有必要保留一部分电量作为安全储备，而不是首次抵达充电站后就完全耗尽电量。根据比亚迪E6 在城市区域性能可知，100%荷电状态下的最大行驶距离约为250 km。假设电动汽车具有相同的电池容量，满荷电状态记为′，电动汽车在满电荷状态下可行驶的最大距离表示为，则电动汽车在荷电状态为时，可继续行驶的距离为：

若电动汽车首次抵达充电站后，当前充电站发生溢出（当充电站高峰时期访问量和平均访问量与总体充电站的平均访问量偏差75%时，将该充电站视为溢出站点），电动汽车司机将会选择其附近其他充电站进行充电。由于过度的放电会缩短蓄电池的使用寿命，电动汽车再次选择充电的充电站与当前充电站距离不能大于D。值得注意的是，电动汽车用户在选择范围D内的充电站充电的偏好会有所差异。越受欢迎的充电站，电动汽车选择在该充电站充电的可能性也就越大。因此，给定不同充电站的平均访问频率(s)，可以将访问频率作为充电站的权重：

如图2 所示，空心圆圈代表充电站，当电动汽车首次抵达充电站时，会发生两种情况：（1）充电站没有发生溢出，电动汽车正常充电；（2）充电站发生溢出，电动汽车无法正常充电，转向附近其他充电站进行充电。本文主要探讨研究第二种情形。充电站的溢出状态分别用0 或1 表示，其中1 表示充电站溢出，0 表示充电站没有发生溢出。假设电动汽车司机在选择二次充电过程中会倾向选择距离充电站最近的充电站充电，降低充电访问成本，因此距离同样会影响司机对充电站的选择。 D为电动汽车首次抵达充电站后并未充电而再次改变充电站的最大可接受充电距离，l表示充电站到充电站s的距离，(s) 表示充电站s的权重。由图2 可知，当l＜D时，在充电站的电动汽车二次充电才有可能选择s作为充电点。当d＞D时，电动汽车剩余电量无法抵达充电站s，因此充电站s并不在司机考虑改变充电位置的范围内。

图2 充电站的选择Fig.2 Choice of charging station

2.3 电动汽车充电热点和移动模式

电动汽车进入充电站充电具有很大的随机性，文献[12]表明该过程符合M/M/排队论模型，第一个M 表示电动汽车一定时间内到达充电站充电过程满足泊松分布；第二个M 表示各个充电桩的服务时间服从负指数分布；代表充电站内充电桩的数量，则存在以下恒定等式：

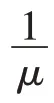
电动汽车访问充电站的次数越多，充电站越繁忙，在该区域越处于重要地位，可以有效服务更多电动汽车用户，进而形成电动汽车充电热点。图3 给出了某区域的充电热点，其位于一个比较受欢迎的购物中心内。进一步观察发现，电动汽车在热点完成充电后的出行模式呈现出星形移动模式，即电动汽车会从相同的起点出发，到达不同的目的地，如图3中的红色箭头所示。

图3 充电热点和星形移动模式Fig.3 Charging hot spot and star-shaped mobility pattern

3 使用效益评分函数

本文将优先被选入最佳网络的充电站视为父级充电站（parent charging station,PS），未扩展或后扩展的充电站称为子级充电站（child charging station,CS）。给定父级充电站，并基于充电站间的访问权重、距离关系和竞争关系计算充电站网络中其他未被选择的子级充电站使用效益分数，计算方法如下：

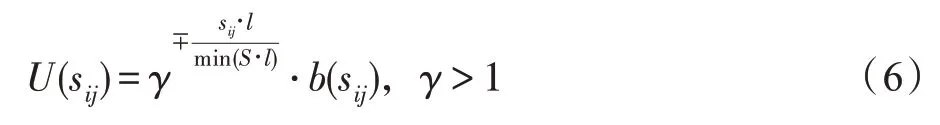
4 充电站网络优化方法

问题定义：给定一个具有溢出状态的充电站集合={,,…,s}，溢出状态集合，访问权重集合，充电站间最短路径距离矩阵∈R，个充电热点和调优参数。充电站网络优化目标是发现冗余充电站集合⊆和获得最佳充电站集合′⊆，目标遵循最大化充电站使用效益，函数形式如下：

其中，(s)表示充电站s的使用效益评分。

4.1 基于充电热点的网络扩展算法

充电站网络扩展算法的基本思想是以个电动汽车充电热点作为网络扩展的起始站点，并不断向最佳站点（即使用效益最高的充电站）扩展，形成一个新的充电站网络。实现算法分为初始化阶段、网络拓展阶段和终止阶段。算法1给出了相应的伪代码。

基于充电热点的网络扩展算法

输入：充电站集合，溢出状态集合，充电站访问权重集合，最短路径距离矩阵，充电热点，调优参数。

输出：最佳充电站网络′，冗余充电站集合。

初始化阶段：第1～4 行，算法首先选择个电动汽车充电热点插入结果集′中，成为父级充电站，并将与父级充电站对应的未被选择的子级充电站插入候选集合，通过-′更新充电站集合。

网络扩展阶段：在每次网络扩展迭代中，当!=∅时，遍历结果集′的父级充电站，判断是否存在溢出站点，对应两种情况的处理方法如下：

（1）如果结果集′中存在溢出充电站，把溢出站点相应的所有未被选择的子级充电站插入候选集′,并基于所有溢出的父级充电站计算集合′中的子级充电站的使用效益分数，计算方法为式（6），并把计算结果插入列表（第7～10 行）。遍历列表并将最佳子级充电站（即使用效益评分最高的站点）扩展到网络，接着将插入到结果集′，然后将未被选择的子级充电站插入候选集合（第8～13 行）。接着，算法将父级站点溢出部分用户和在的D范围内未被扩展的充电站充电的用户重新分配给新站点，并重新计算新站点的溢出状态。第14～17 行，若没有发生溢出，表示新站点能够覆盖其D范围内的未被选择的充电站，并解决其父级充电站的溢出问题。这表明了新站点的D范围内未被扩展的子级充电站皆为冗余充电站，这类充电站的产生往往是因为缺乏对电动汽车充电需求的合理的分析。因此，把这些可被覆盖的充电站插入冗余站点集合中，并更新父级充电站的溢出状态为0，通过--更新。第18～21行，若重新分配用户后，新站点发生溢出，则表明无法覆盖其D范围内未被选择的充电站，通过-更新。再次计算父级充电站溢出部分用户重新分配给新站点是否会导致的溢出。若新站点没有发生溢出，表明新站点能够解决其父级充电站的溢出问题，并将父级充电站溢出状态更新为0。

（2）如果结果集′中充电站不存在溢出，算法直接计算候选集合中的所有子级充电站的使用效益分数，并将最大使用效益的子级充电站扩展到网络中。然后，将新被扩展的充电站未被选择的子级充电站插入候选集中成为新的候选站点（第22～26 行）。算法将在新站点的D范围内未被选择的充电站充电的用户重新分配给新站点，并重新计算的溢出状态。第27～29 行，若没有发生溢出，表示新站点能够覆盖其D范围内未被选择的充电站，并把这些充电站插入冗余站点集合，通过--更新。第30～31 行，若重新分配用户后，发生溢出，则表明无法覆盖其D范围内的未被选择的充电站，通过-更新。

终止阶段：第33 行，当=∅时，即遍历完所有充电站时，算法终止扩展循环，返回包含溢出状态的最佳充电站网络方案′和冗余充电站集合。

4.2 初始化方法

算法1 的最终结果′的性能很大程度上取决于初始充电站的选择，因此如何选择有效的初始化方法成为网络扩展算法的关键。以下提出了两种不同的初始化方法：

（1）基于top-的初始化。网络扩展中最直接的初始化方法是top-初始化，其本质是选择电动汽车访问率最高的充电站（即充电热点）作为网络扩展的起始站点。因为优化方案中应该始终包含电动汽车充电热点，确保算法不会遗漏任何使用效益最高的充电站，方法的本质是为了覆盖更多的用户。然而，大部分访问率高的充电站在空间分布上非常接近，特别是当充电站的数量较少的时候会导致网络扩展过程中有可能遗漏一些重要的区域。

（2）基于聚类的初始化。为了在初始化阶段包含更多空间多样性的起始站点，以及在充电站数量较少时网络扩展更有效，提出了基于空间聚类的方法来选择网络扩展的起始站点。采用基于空间聚类的初始化方法的原因来自对电动汽车充电热图的观察（如图4 所示）。从热力图可以看出，在空间上电动汽车充电行为的分布已具有一些可视化的集群，本文采用的是基于层次聚类的聚类方法产生集群。最后，选择每个集群中访问率最高的充电站作为起始站点。

图4 电动汽车充电行为空间分布Fig.4 Spatial distribution of charging behavior of electric vehicles

5 实验及结果分析

实验数据采用武汉市中心区域的充电站网络，区域内共有156 个充电站（实心圆表示），充电站的空间分布如图5 所示。网络中充电站的平均使用效益约为61.04%，共有32 个溢出站点（红色实心圆表示）。将网络中充电站按照到达率大小进行排序，选择前20%的充电站作为城市电动汽车的充电热点。

图5 武汉市中心区域的充电站网络Fig.5 Charging stations network of central area of Wuhan

5.1 参数设置

（1）不同值的影响。实验将值分别设置为{5,10,15,20,25}来观察网络扩展算法起始站点个数的不同对充电站网络优化的影响。图6（a）为对充电站网络上进行不同值优化，采用top-方法和聚类法的用户覆盖率结果对比图。如图所示，两种初始化方法在5 ≤≤10 时，用户覆盖率相同。原因是在这个范围内两种初始化方法的起始站点是相同的，所得到的优化方案一致。然而，在大多数情况下top-方法具有更高的用户覆盖率和更低的充电站溢出率（如图6（b）所示）。实验结果表明，当5 ≤≤20时，两种初始化方法溢出率基本保持一致，但top-方法具有更高的用户覆盖率，提高约3 个百分点，并且随着值的增大，用户覆盖率持续上升。因此，本文将初始化方法的最佳值设置为25。

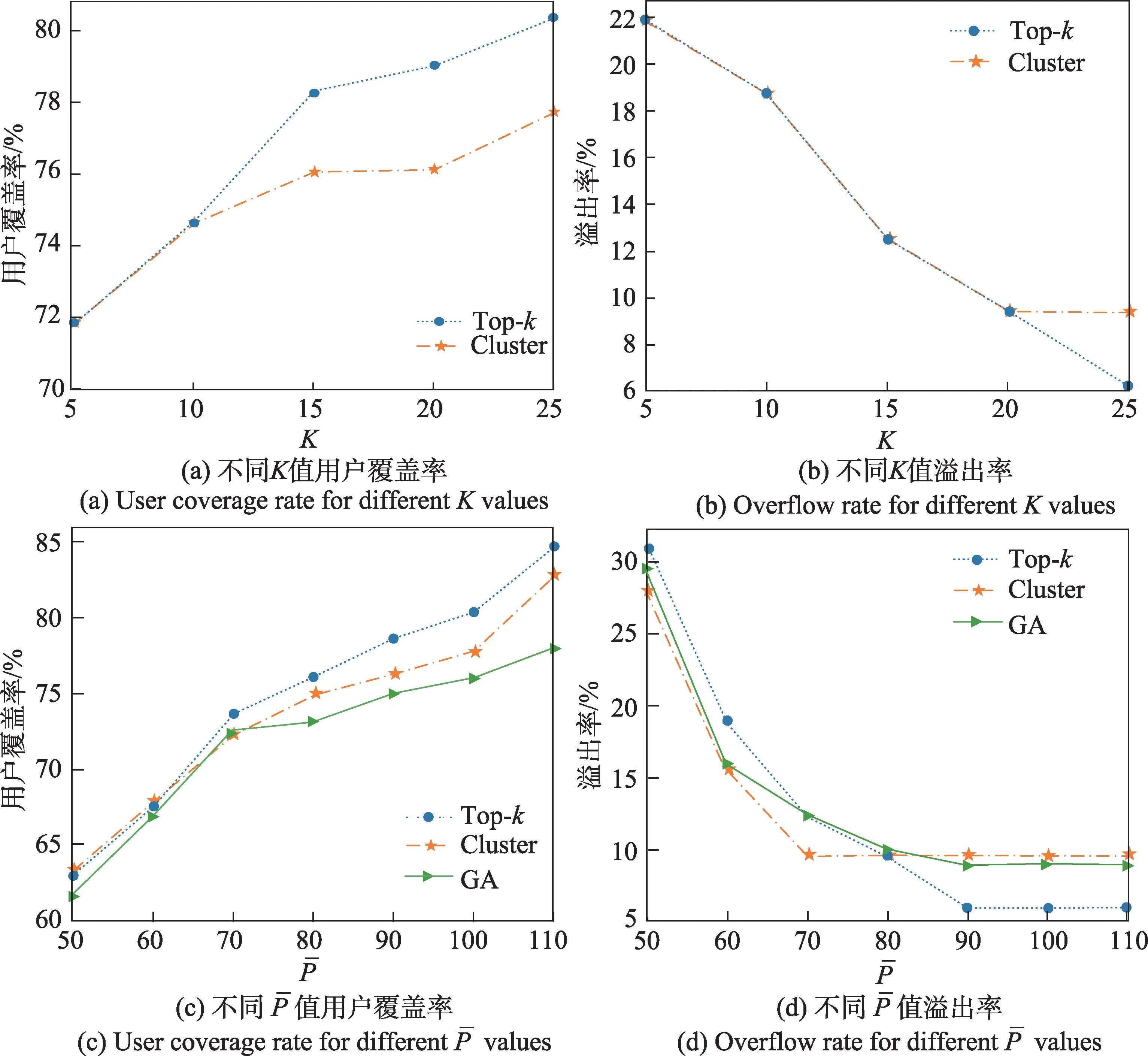
图6 效能评估Fig.6 Effectiveness evaluation

5.2 网络优化结果分析

充电站利用率是衡量整个充电站网络使用情况的直观指标。充电站一天内（24 h）平均利用率的计算公式如下：

如表1 所示，优化后得到的最佳充电站网络的充电站平均利用率比原网络提高了约7.72 个百分点，用户覆盖率高达97.63%，并且溢出站点数量减少了21，原因是网络中部分充电站的溢出主要由用户充电习惯所导致，并非真正的溢出，可以通过区域内其他充电站平衡充电压力。然而，在部分区域内充电站整体缺桩情况下，政府部门只能通过新增站点来缓解本地的充电压力（如图7 所示的C 区、D 区、E 区、G 区和F 区）。这些区域主要由大量高访问率的充电站和溢出充电站构成。从优化结果可知，原充电站网络存在大量冗余充电站（充电站ID 分别为15、62、81、82、84、93、100、109、131、139、144 和148），空间分布如图7 黑色实心圆所示。在网络优化过程中，逐一将冗余充电站从网络中移除来优化充电站网络，减少公共资源的浪费，并在一定程度上提高充电站利用率。

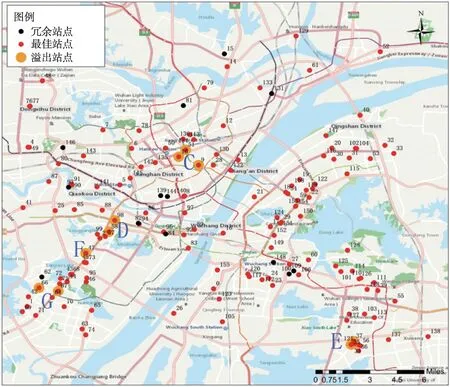
图7 武汉市中心区域最佳充电站网络Fig.7 Optimal charging station network for Wuhan central area

表1 优化结果Table 1 Optimization results

6 结束语

本文分析了影响充电站网络优化的相关因素，建立了以充电站使用效益最大化为目标函数的优化模型。在充电站网络优化过程中，兼顾充电站溢出、充电站相互作用和电动汽车偏好，并以最大使用效益为指标选择最佳充电站位置。最后，以武汉市中心区域充电站网络为例进行研究，发现武汉市中心区域的充电站网络出现了两种极端现象：充电站供不应求和供过于求。原因是因为充电站分布与电动汽车充电需求分布不一致，缺乏对现实充电站网络布局的合理性分析。实验结果表明，本文方法和模型不仅能够有效诊断并消除充电站网络中的冗余充电站，提高充电站的利用率，减少公共资源的浪费，还能识别网络中的充电站拥堵区域，发现布局漏洞，为政府进一步解决电动汽车充电难问题提供参考。后续研究中，将进一步考虑如何精确地在充电站拥堵区域新增站点，解决充电难问题。