高光谱协同稀疏与非局部低秩张量变化检测

詹天明，宋 博，孙 乐，万鸣华，杨国为

1.南京审计大学 信息工程学院，南京211815

2.南京审计大学 审计信息工程与技术协同创新中心，南京211815

3.南京信息工程大学 计算机学院，南京210094

变化检测是地球科学以及遥感领域研究最多的问题之一。它的任务是利用同一场景的两个或多个时间点的图像，以检测不同时间点内发生的变化。其应用范围包括自然灾害监测、城市和森林的长期跟踪、农作物的生长状态观测、土地资源开发利用审计等。变化检测从任务角度主要分为：判断是否发生变化、变化位置定位、变化发生的种类等。而变化检测过程主要包括预处理、变化检测算法和效果评估这三个步骤。其中，变化检测算法是其核心步骤。目前，常被用于变化检测的主要有合成孔径雷达图像、全色图像、多光谱图像以及高光谱图像。具有高光谱分辨率的高光谱图像可以提供比其他遥感图像更丰富的光谱信息，因此高光谱图像常被用于识别细微变化，反映出不同物体的详细成分等问题。近年来，基于高光谱图像的变化检测被很多学者广泛研究，但其较低的空间分辨率、光谱维冗余信息以及较少的数据集都给高光谱变化检测方法的发展带来了较大影响。

近年来，基于二分类的变化检测方法较为常见，它的目的是将多时相遥感影像划分为变化类和非变化类。Malila提出了变化向量分析（change vector analysis，CVA）方法，该方法计算两个时相的光谱变化向量，再根据变化幅度和变化方向判定每个像素点是否发生变化。在此基础上，Baisantry 等人提出了基于增强主成分分析（principal component analysis，PCA）和反三角函数阈值的变化矢量分析方法（PCA-CVA）。该方法核心思想是用两时相图像的主成分差分和反三角函数合理选择阈值，进而判定当前像素点是否发生变化。Nielsen 等人利用典型性相关分析的降维属性提出多元变化检测（multivariate alteration detection，MAD）方法，该方法通过求解多元变化值以判断各个像素是否在时间维上发生变化。此后，Nielsen 在多元变化检测方法基础上提出了迭代加权多元变化检测方法（iteratively reweighted MAD，IR-MAD），该方法在迭代步骤中对每个像素赋予的权重进行更新，迭代结束后以权重作为判断像素是否变化的标准。

基于监督的遥感影像的变化检测方法也被广泛研究。其中一类方法的主要思想是通过监督学习对各时相遥感图像进行分类，然后根据每个像素点在不同时间点上的类别信息进行变化检测。Bovolo 等人提出的变化检测框架中先对两时相的遥感影像分别进行逐像素分类，如果一个像素点在两时相的影像中分类不同，就可以认为这个像素点产生了变化。另一类方法是对差异图像进行监督分类，将差异图像分为变化和非变化两类，从而完成变化检测任务。Nemmour 等人提出了多支持向量机（multiple support vector machine，Multiple SVM）的变化检测方法，该方法先对变化图像进行二分类，再用模糊积分和吸引子动力学指标对分类结果进行优化。随着深度学习方法的发展，基于深度学习的高光谱变化检测方法也被广泛研究。Wang 等人提出端到端2D 卷积神经网络框架的高光谱变化检测方法。该方法利用两时相的光谱信息以及解混结果为每个像素点构建一个混合矩阵，再用卷积神经网络进行分类。

虽然遥感变化检测方法被广泛提出，但受限于高光谱图像的低空间分辨率和高光谱分辨率，直接应用于高光谱变化检测时其精度都不是太高。而现有基于深度学习方法的高光谱变化检测方法需要大量的训练样本才能保证较高的检测精度。此外，这些方法需要将三维高光谱图像转换为二维矩阵，一定程度上破坏了高光谱图像空间关联性。为解决该问题，将三维高光谱图像表示为一个张量的形式进行处理，在高光谱图像降维、解混、分类和融合中引起了广泛关注。张量模型利用多线性代数的强大框架，可以联合利用光谱和空间信息，有助于提升后续高光谱图像处理的性能。

目前，张量建模在高光谱图像融合以及分类领域已得到较为广泛的研究，但在高光谱变化检测问题中利用张量进行建模的方法较少。为充分利用张量模型中空谱联合特征以提高高光谱变化检测精度，本文提出一种基于协同稀疏与非局部低秩张量的高光谱变化检测方法。该方法首先求得两相位的高光谱差分图像，再根据差分图像中图像块非局部特点，提取不同的非局部相似张量簇。然后基于协同稀疏正则化和低秩正则化建立变化检测模型，利用极小化方法求解得到表示系数。最后根据表示系数求出张量在变化和非变化两类中的投影残差，由投影残差判断该张量是否发生变化。该方法主要有如下两个优点：（1）将非局部图像块组合在一起形成一系列低阶张量，可以深挖高光谱空谱联合信息，同时降低维度；（2）协同稀疏表示分类可以在较少的训练样本下保证一定的分类精度，且在高光谱图像稀疏分解方面比传统的低阶正则化分类器具有更好的性能，从而克服高光谱变化图像数据集不足的问题。在仿真和真实数据集中进行对比实验，结果表明本文方法可以取得较好的高光谱变化检测精度。

1 高光谱图像的张量表示

设χ ∈R为-阶张量，各个I表示模式，张量中的每个元素表示为x。阶张量的F 范数和范数定义为：

阶张量沿模展开表示为∈R，将还原成张量则可表示为χ=fold()，其中fold是张量沿模展开的逆操作。设∈R表示大小为J×I的矩阵，和χ 的阶积运算定义为：

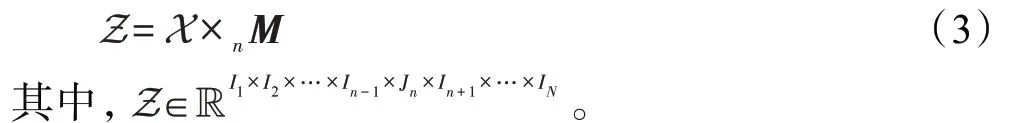
设J∈R表示高光谱图像，∈R是字典，S ∈R是系数张量，N∈R是噪声。它们之间的关系可以表示为：

其中，、表示高光谱图像的空间维的高和宽，表示高光谱图像的波段数，表示字典中的原子个数。

2 本文方法

本文方法首先将两时相图像J和J做差分取绝对值得到J=|J-J|∈R，然后对差异绝对值图建立字典={,}∈R，其中、分别表示变化和不变区域的子字典。建立基于协同稀疏与非局部低秩张量正则化模型，求出J 在字典中的表示系数，最后根据其在两个子空间的投影残差判断每个像素是否发生变化。总体流程图如图1 所示。

图1 本文方法总体流程图Fig.1 General flow chart of proposed method

2.1 协同稀疏模型

由式（4）高光谱图像在字典下的建模方式，两时相图像差异绝对值图像可建模为：

其中，S ∈R是未知的表示系数的张量形式，N∈R是残差。根据表示学习理论，通过求解如下优化问题即可求得表示系数S ：

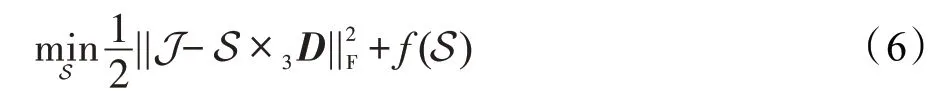
其中，(S)是S 的先验函数。在表示学习理论中，将系数的张量形式乘以字典，必然导致系数的张量形式在空间维上仅包含少量非零值，但在最近邻理论中，每个像素点与字典中的少数原子具有较强的相关性，因此每个像素点在字典下的表示系数应该具有稀疏性。为此，基于上述先验，建立如下协同稀疏模型：

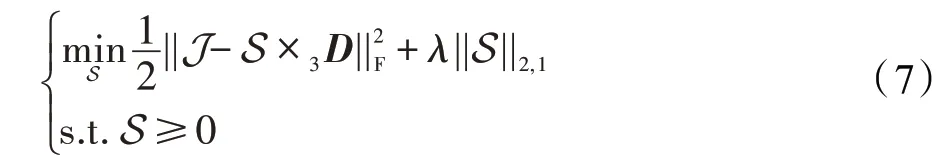
根据文献[15]，协同稀疏正则项||S||定义如下：

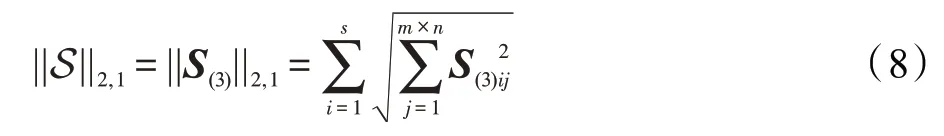
2.2 协同稀疏与非局部低秩张量分解模型

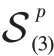
将上述局部张量块应用于整个图像域中，表示系数张量形式S 的核范数可表示为：

将式（9）与式（6）相结合，得到如下的协同稀疏与非局部低秩张量模型：

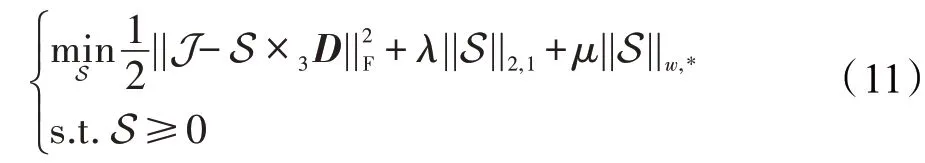
其中，是非负常数，第一项是求得J 在字典中的一个投影系数，而第二项则体现了该系数的协同稀疏先验，第三项S 的核范数即为图像的非局部低秩约束，体现了该系数的空间非局部相关性先验。对该模型极小化即可得到J在字典中最优表示系数。

2.3 优化算法

模型（10）无法直接求解，为此采用交替方向乘子法将目标函数转化为如下多个子问题分别求解：

其中，U、U、是引入变量。式（11）的拉格朗日方程可表示为：

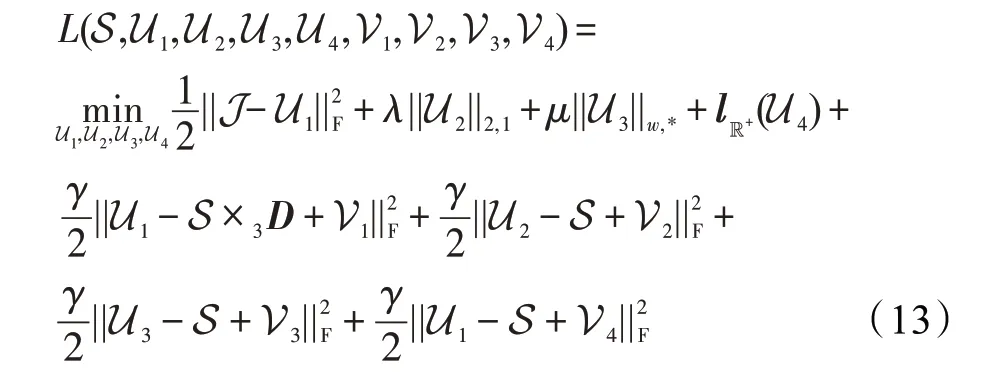
其中，是拉格朗日惩罚因子，V、V、V、V是拉格朗日乘子，是惩罚函数，当≥0 时，()=0，当＜0 时，()=+∞。

由交替方向乘子法，上述变量可通过交替迭代方式求解。求解变量S 的目标函数为：

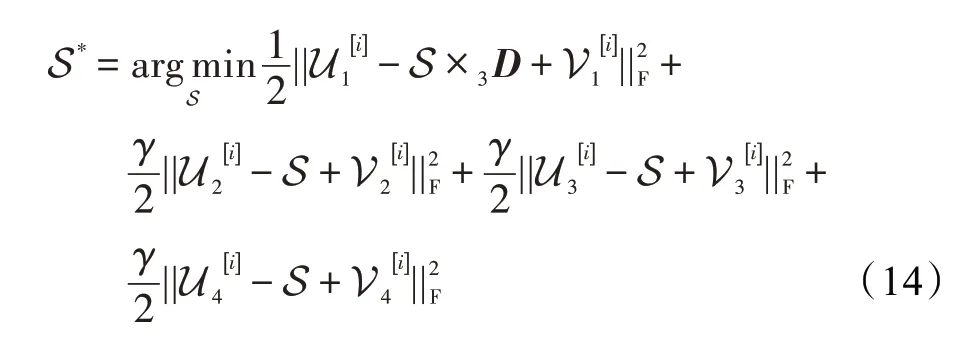
其迭代解为：

其中，是单位矩阵，是的转置。

求解变量U、U、U、U的目标函数为：

其中，函数表达式为：

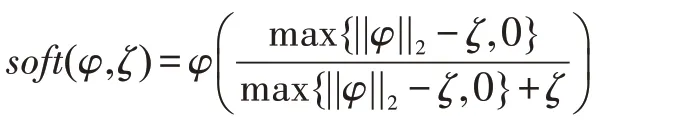
函数表达式为：

(,)=diag(max{()-,0})(·)表示奇异值分解。

拉格朗日乘子V、V、V、V更新步骤为：

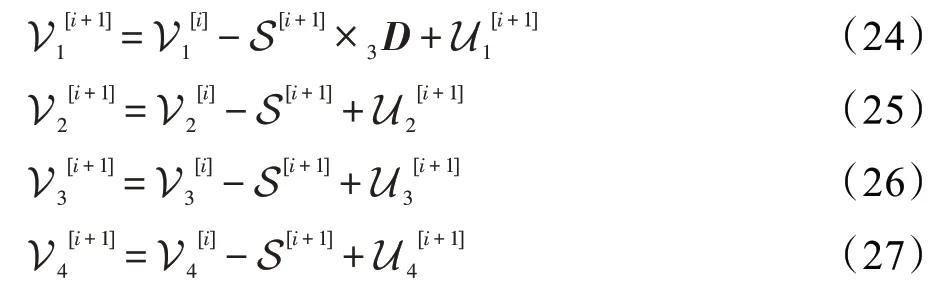
本文方法的总体算法步骤如下：

基于协同稀疏与非局部低秩张量的高光谱变化检测算法

输入：第一时相高光谱图像J，第二时相高光谱图像J。

3 实验结果与分析

3.1 数据集

实验采用了3 组数据，第一组是Farmland 数据集，第二组和第三组是UASFC（Urban area in San Francisco City）数据集。

Farmland数据集是由EO-1（Earth observing-1）Hyperion设备采集的2006年5月3 日 和2007 年4 月23 日江苏省盐城市一个农田的高光谱图像。其光谱范围为0.4～2.5 μm，光谱分辨率10 nm 左右，空间分辨率大约为30 m。该图像共包含155 个波段，空间大小为450×140 像素。两相位伪彩色图及真实变化图如图2 所示。

图2 Farmland 数据集Fig.2 Farmland dataset

UASFC 数据集是由无人机机载传感器采集的2009年9月18日和2015年5月11日旧金山市市区的高光谱图像。拍摄频率为1.26 GHz，光谱空间分辨率为1.66 m，方位分辨率为1 m，入射角为25°～65°。共两组数据：第一组数据（UASFC1）空间大小为200×200 像素，含138 波段；第二组数据空间（UASFC2）大小为100×100 像素，含138 波段。两相位伪彩色图及真实变化图如图3 和图4 所示。

图3 Urban area in San Francisco City 第一组数据集Fig.3 The first dataset of Urban area in San Francisco City

图4 Urban area in San Francisco City 第二组数据集Fig.4 The second dataset of Urban area in San Francisco City

3.2 模型评价指标

本文使用总体准确度（overall accuracy，OA）和Kappa 系数两个指标评估模型的变化检测效果。为了计算OA 和Kappa 值，需要统计模型对每个像素的预测情况：模型正确分类了变化的像素数量记为真阳性（true positive，TP）；模型正确分类了未变化的样本数量记为真阴性（true negative，TN）；模型错误地将未变化的像素分类为变化像素的数量记为假阳性（false positive，FP）；模型错误地将变化的像素分类为未变化像素的数量记为假阴性（false negative，FN）。记为像素总数，则有：

用于衡量模型正确的分类像素比例，计算公式为：

Kappa 系数衡量模型预测结果和地面真值图的一致性，计算公式为：

其中，p的计算公式为：

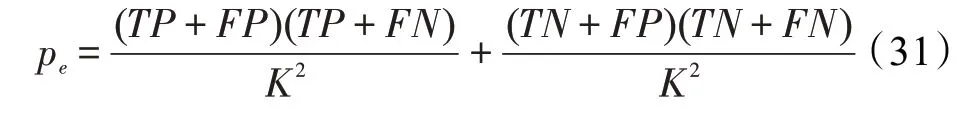
3.3 参数设置及分析

本文的迭代终止条件为=10，若迭代次数超过30 次尚未达到该条件则终止迭代。本文模型中的两个参数和分别控制联合稀疏约束项和非局部低秩约束项，其值较低时约束较小，空谱联合特征不明显，检测结果中噪声过多会导致精度下降；而当其值较高时约束较大，检测结果过多地受到空谱联合约束的影响，数据本身对变化检测的决策能力下降，变化检测精度也不高。为此，根据各项的数值量级关系取∈[0.000 5,0.003 0],∈[0.001 0,0.005 0] 进行实验。图5 显示了不同的和值下，本文方法的检测精度。从图中结果可以看出，本文方法在=0.001 0 和=0.002 5 时取得最优的检测精度，且在∈[0.001 0,0.002 5]，∈[0.001 0,0.005 0]的范围内都保持一个较高的检测精度。

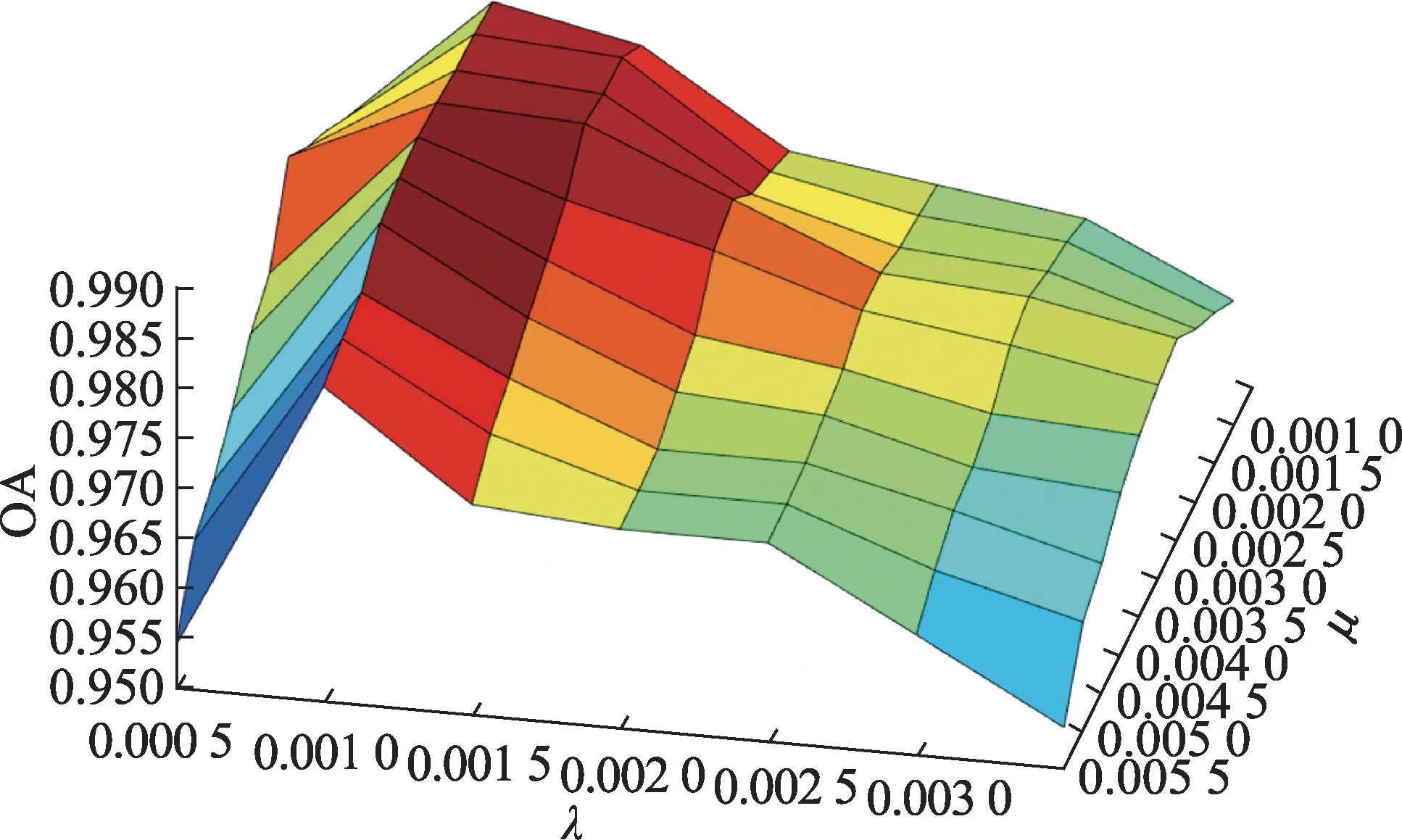
图5 选取不同参数时三组数据集的平均OA 值Fig.5 Average OA values of three datasets with different parameters

对于监督学习的方法，训练样本个数对变化检测精度的影响也是比较敏感的。为此，本文在每个数据集中的训练样本总数取1 000 到8 000 进行实验，其中正负样本个数各占50%。图6 显示了不同训练样本个数下本文方法的变化检测精度。从图中可以看出，本文方法在Farmland 数据集中选取2 000 个训练样本即可得到较高的检测精度，在Urban area in San Francisco City 两组数据集中选取4 000 个训练样本得到较高的检测精度。

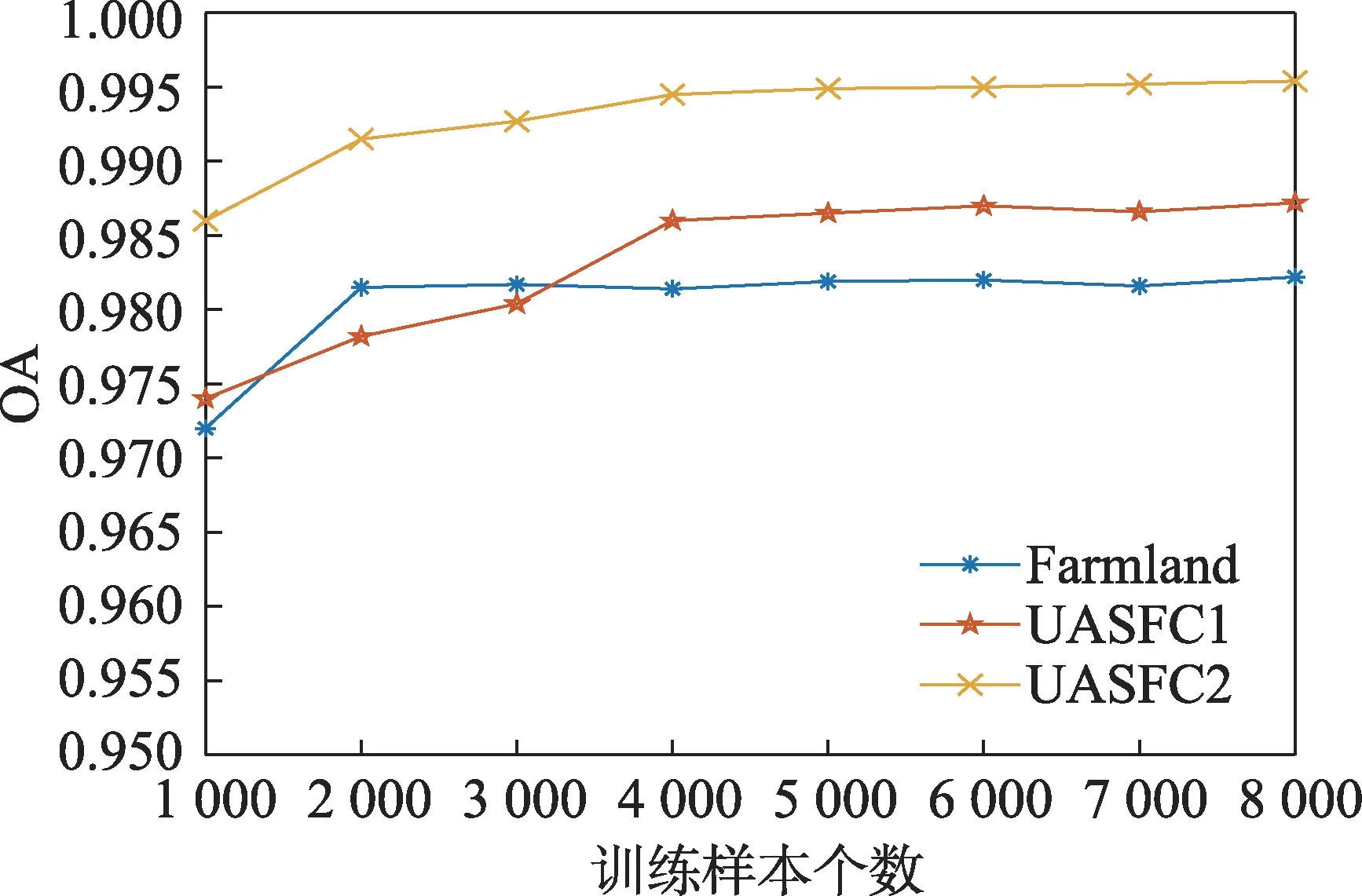
图6 三组数据集取不同训练样本数量时的OA 值Fig.6 OA values of three datasets with different number of training samples

本文方法需要选择图像块构造非局部张量，为选择最优尺度的图像块，分别选取3×3，5×5 和7×7 三种尺度在Farmland、UASFC1 和UASFC2 数据集上进行变化检测。对应的OA 值如表1 所示。从表中可以看出，图像块尺度为3×3 大小时，本文方法在3 个数据集上都能取得较好的OA 值。这是因为在高光谱变化检测问题中，变化区域包含有很多较小且不规则的图像块。若尺度较大，会对这些图像块进行平滑，从而影响变化检测的精度。在本文实验中，选取3×3 大小的图像块构造非局部张量进行变化检测。

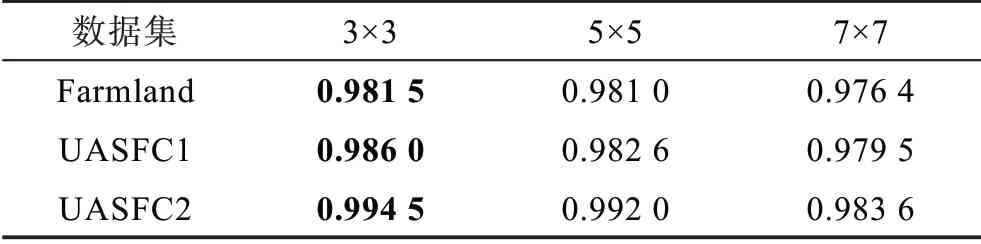
表1 不同尺度图像块在三组数据集上的OA 值Table 1 OA values of different scales image blocks on three datasets

3.4 对比实验

为定量分析本文方法的变化检测效果，选取基于SVM 的变化检测方法、基于卷积神经网络（convolutional neural network，CNN）的变化检测方法、基于解混和CNN 的变化检测方法（general end-to-end 2-D CNN，GETNET）、基于低秩约束的变化检测方法（non-local low-rank sparse unmixing，NLLRSU）、基于张量回归的变化检测方法（generalized tensor regression，GTR）以及本文方法去除非局部张量约束的变化检测方法（collaborative sparsity tensor，CST）与本文方法CSNLRT（collaborative sparsity non-local low-rank tensor）进行比较。图7～图9 分别显示了这些方法在Farmland 数据集和Urban area in San Francisco City（UASFC）两组数据集上的变化检测结果。从图中可以看出，基于SVM 的变化检测方法和基于CNN 的变化检测方法在空间上未进行任何约束，检测结果中噪声较多。而GETNET 方法、基于低秩空间约束方法NLLRSU 以及本文方法因使用了空谱联合的约束，检测结果具有较强的抗噪性。表2 给出了这些方法在各个数据集中的OA 值和Kappa 值，从结果中可以看出，本文方法在3 组数据集中都能取得最优的OA 值和Kappa 值。从OA 值和Kappa 值中可以看出，本文所提的张量表示方法可以有效地从两时相高光谱图像中准确检测出变化的部分。此外，本文所提CSNLRT 方法比CST 方法在OA 以及Kappa指标上都取得较好的结果，这说明本文所提变化检测模型中的非局部低秩的约束项在抑制噪声提高检测精度上起到了非常好的效果。由于本文方法利用了非局部张量低秩建模以及迭代求解，本文方法的运行时间较长。

图7 不同方法在Farmland 数据集上的检测结果Fig.7 Detection results of different methods on Farmland dataset

图8 不同方法在UASFC1 数据集上的检测结果Fig.8 Detection results of different methods on UASFC1 dataset

图9 不同方法在UASFC2 数据集上的检测结果Fig.9 Detection results of different methods on UASFC2 dataset

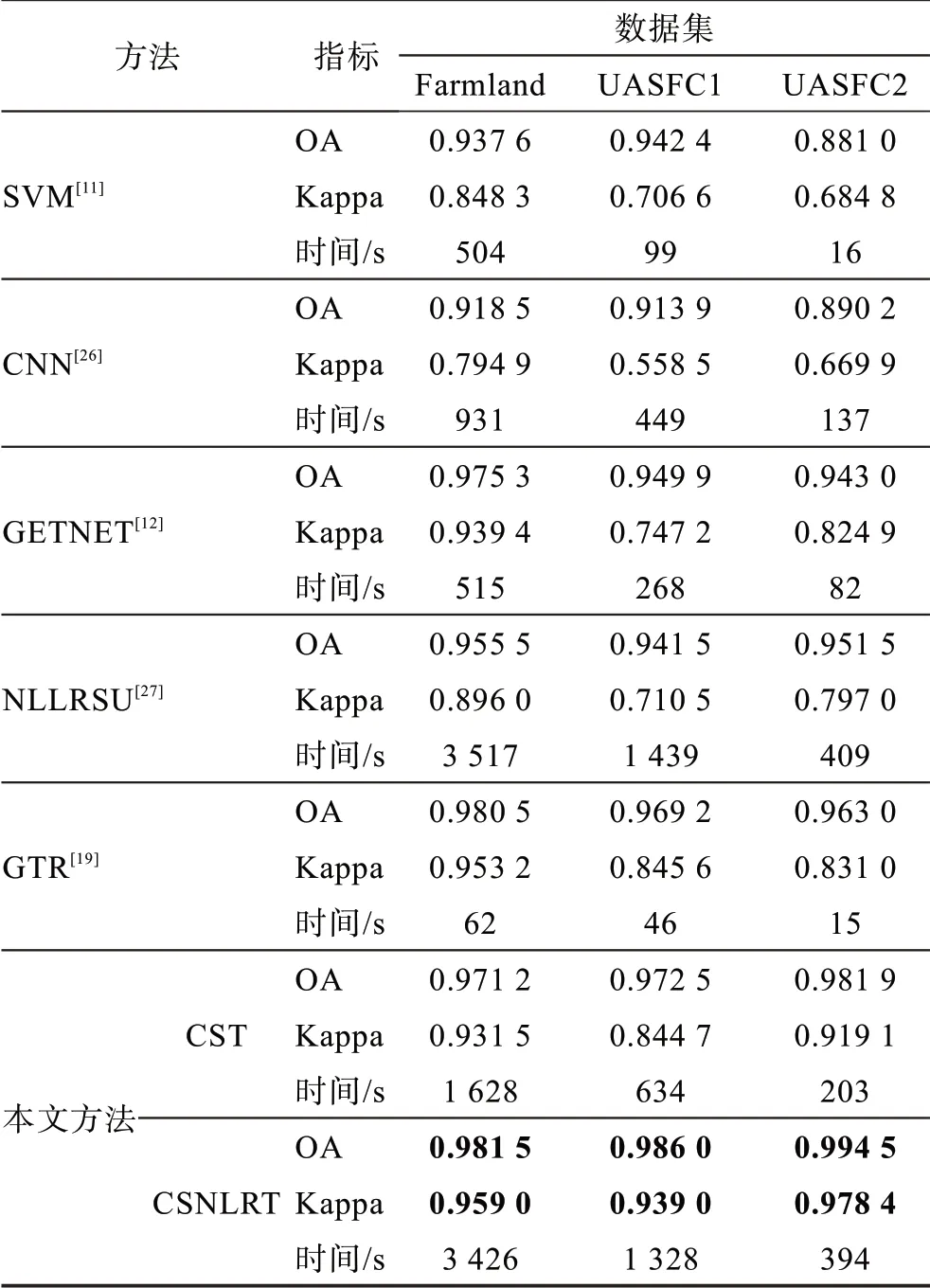
表2 不同方法在3 组数据集上的实验结果Table 2 Experimental results of different methods on 3 datasets

4 总结

本文针对高光谱变化检测问题，提出一种基于协同稀疏与非局部低秩张量的高光谱图像变化检测方法。该方法首先求得前后时间点的高光谱差分图像，再根据差分图像中图像块的非局部分布特点，提取不同的非局部相似张量簇。然后基于协同稀疏正则化和低秩正则化建立变化检测模型，利用极小化方法对模型求解得到表示系数。最后根据表示系数求得张量在不同类别中的投影残差，进而判断该张量是否发生变化。在Farmland 和UASFC 数据集中进行实验，本文方法的OA 和Kappa 值都优于其他方法所得结果，表明本文方法在两时相高光谱数据变化检测任务中可以取得较好的检测精度。