新颖的离散差分演化算法求解D{0-1}KP 问题

张发展，贺毅朝，刘雪静，王泽昆

河北地质大学 信息工程学院，石家庄050031

背包问题（knapsack problems，KP）是一类经典的NP 完全问题，也是重要的组合优化问题。KP 在资源分配、投资决策、经济金融和信息安全等诸多领域都具有重要的理论意义和实用价值。KP 有许多不同的扩展形式，例如：集合联盟背包问题（set-union knapsack problem，SUKP）、多维背包问题（multidimensional knapsack problem，MKP）、具有单连续变量背包问题（knapsack problem with a single continuous variable，KPC）和折扣{0-1}背包问题（discounted{0-1}knapsack problem，D{0-1}KP）等。

D{0-1}KP 是由Guldan于2007 年首次提出的0-1KP 的一种更复杂的扩展形式。由于D{0-1}KP 对项目（物品）的选择更加多样化，使得D{0-1}KP 比0-1背包问题（0-1 knapsack problem，0-1KP）具有更大的挑战性。目前，许多国内外学者对D{0-1}KP 问题的求解算法进行了研究，例如Guldan讨论了如何使用启发式和精确算法求解D{0-1}KP，并给出了一种求解D{0-1}KP 的动态规划法；Rong 等人于2012 年通过核问题将D{0-1}KP 划分为若干较容易的子问题，并给出了一种动态规划与核相结合求解D{0-1}KP的精确算法；2016 年，He 等人设计了一种新的基于动态规划的精确算法，并在此基础上提出了三种近似算法求解D{0-1}KP；贺毅朝等人于2016 年首先建立了D{0-1}KP 的两个新的数学模型，在提出了两种贪心修复与优化算法的基础上，给出了两种利用基于杰出者保留策略遗传算法（genetic algorithm with elitist reservation strategy，EGA）求解D{0-1}KP 的方法；吴聪聪等人首先采用双重编码解决D{0-1}KP的编码问题，在此基础上提出了一种变异的蝙蝠算法（mutated double binary bat algorithm，MDBBA）求解D{0-1}KP；2018 年，刘雪静等人针对D{0-1}KP 的两种数学模型，提出了自适应细菌觅食算法（adaptive bacterial foraging algorithm，ABFO）求解D{0-1}KP的两种算法，并比较了两种算法的优劣；随后，He等人先后提出了基于群论的优化算法（group theorybased optimization algorithm，GTOA）和基于环理论的演化算法（ring theory-based evolutionary algorithm，RTEA），并分别用于求解D{0-1}KP，取得了较好的效果；2020 年，Wu等人提出了一种离散混合教学优化算法（hybrid teaching-learning-based optimization algorithm，HTLBO），并利用它给出了一种求解D{0-1}KP的方法；Li等人在提出一种新V 型传递函数的基础上，提出了一种新的二进制鲸鱼优化算法（discrete whale optimization algorithm，DWOA），并应用于求解D{0-1}KP 问题。显然，目前求解D{0-1}KP 的算法主要分为两类：精确算法和非精确算法。精确算法具有伪多项式时间复杂度，不适用于求解大规模D{0-1}KP 实例。非精确算法特别是演化算法不仅求解速度快，而且计算结果能够满足实际应用的需求，因此探讨利用演化算法求解D{0-1}KP 的高效方法是一个值得研究与探讨的问题。

差分演化（differential evolution，DE）最初是由Storn 和Price提出的一种基于随机种群的元启发式算法，虽然在求解数值优化和电力系统等问题时表现出优异的性能，但是由于差分演化是基于实数运算实现的，不能直接应用于求解组合优化问题。为此，研究人员先后提出了不同版本的二进制差分演化算法，例如Engelbrecht等人于2007 年利用S 型转换函数提出了一种二进制差分演化算法（binary differential evolution，BinDE）。He 等人基于混合编码机制提出了一个二进制差分演化算法（binary differential evolution algorithm with hybrid encoding，HBDE），利用满射映射由个体的实向量得到一个0-1向量，从而使HBDE 适于求解以0-1 向量为可行解的组合优化问题。但是从相关文献中不难看出，BinDE利用S 型转换函数将DE 中个体的实向量编码转换为0-1 向量编码的概率与一个随机数进行比较，容易造成可行解中0 和1 分布的不确定性。与BinDE恰恰相反，HBDE 利用满射映射的方法容易造成可行解中0 和1 分布过于均匀。在大量实验的基础上发现，上述已有的二进制差分演化算法求解D{0-1}KP的实验结果较差，并不能令人满意。为此，本文给出了一种新V 型转换函数（novel V-shape transfer function，NV），并在此基础上提出了一种基于新V型转换函数的新离散差分演化算法（novel discrete differential evolution algorithm，NDDE），给出了求解D{0-1}KP的一个新的高效方法。

1 D{0-1}KP 的定义和模型

D{0-1}KP 问题是经典0-1KP 的一个更复杂的变体，它在0-1KP问题的基础上加入了“折扣”思想，当同时选择两个物品时就会得到折扣。这种思想来源于商业领域，商场和企业通常会通过“折扣”的方式吸引更多的消费者。D{0-1}KP问题在项目决策、资源投资和资本预算等诸多领域具有重要的应用理论意义。

下面给出D{0-1}KP问题的定义和已有数学模型。

D{0-1}KP 的定义一般描述为：给定个含有3个物品的物品集，物品集(0 ≤≤-1)中含有的3 个物品分别表示为3，3+1 和3+2，其中前两个物品3和3+1 的价值系数分别记为和，重量系数分别记为和；第三个物品3+2 为前两个物品的合并，它的价值系数为=+，它的折扣重量系数为，满足＜+，并且＜、＜。对于每一个物品集(0 ≤≤-1)，物品3、3+1 和3+2 中至多有一个可以被选择装入背包中。D{0-1}KP 问题的目的是如何选择物品装入背包，使得装入背包的所有物品的重量系数之和在不超过背包载重的前提下价值系数之和达到最大。

根据上述定义，Guldan给出了D{0-1}KP 的第一个数学模型，其描述如下：

其中，=[,,…,]∈{0,1}为一个3维二进制向量。仅仅表示D{0-1}KP 的一个潜在解，只有当它同时满足约束条件（2）和（3）时才是一个可行解；二元变量x(0 ≤≤3-1）表示物品是否装入背包，x=0 表示物品没有被装入背包，反之x=1 表示物品装入背包中。

He等人根据D{0-1}KP的定义，建立了D{0-1}KP的两个新的数学模型：模型二和模型三。本文仅研究如何基于D{0-1}KP 的第一数学模型进行高效求解，其他两个模型不再赘述，请参考有关文献[12]。

2 利用NDDE 求解D{0-1}KP

本章首先介绍了四种S 型转换函数和四种V 型转换函数，然后提出了一个新V 型转换函数（NV），接着基于NV 提出了一个新的离散差分演化算法（NDDE），并给出其算法原理和伪代码描述。最后，给出了利用NDDE 求解D{0-1}KP 的具体方法。

2.1 新V 型转换函数

目前，已有的演化算法多数都是基于实数运算实现进化的，因此不能直接用于求解二元优化问题。为此，相关研究人员提出一种映射的方法，通过转换函数将个体的实向量编码映射为一个0-1 向量编码，以适合直接用于求解二元优化问题。近年来，转换函数成为二进制演化算法研究的一个热点问题，已有的转换函数可以分为两类，即S 型转换函数和V 型转换函数。其中S 型转换函数分别命名为S1～S4，V 型转换函数分别命名为V1～V4。表1 给出了4 个S 型转换函数和4 个V 型转换函数。

表1 S 型转换函数和V 型转换函数Table 1 S-shaped and V-shaped families of transfer functions

本文受V 型函数的启发，在保留V 型转换函数特性的基础上，提出了一个计算简单的新V 型转换函数，命名为NV。转换函数NV 的计算公式如式（5）所示，其函数曲线如图1 所示。

图1 NVA 的函数曲线Fig.1 Function curve of NVA

从表1、图1 和式（5）可以看出：NV 型传递函数与S 型传递函数相比，两者之间差别巨大，它们明显具有不同的性质。且不难看出，由于S 型函数中涉及指数运算，NV 型传递函数的计算量远远小于S 型传递函数。NV 型传递函数与V 型传递函数相比，虽然两者的函数图像相似，都是关于轴对称的，但是两者之间依然存在较大差异：首先，NV 型传递函数为初等函数，而V 型传递函数中的V1 不是初等函数。其次，NV 型传递函数的计算复杂度明显比V 型传递函数的低。

2.2 NDDE

下面利用新V 型转换函数给出一个新的离散差分演化算法（NDDE）。在保持DE 原有进化模式不变的基础上，利用转换函数NV 将DE 中个体的实向量转化为0-1 向量，实现对D{0-1}KP 问题的求解。

设Y=[y,y,…,y]表示NDDE的当前种群中第个个体，其中y∈[-,]，=1,2,…,,=0,1,…,3-1，为种群规模，3为物品个数。NDDE利用转换函数NV将3维实向量Y=[y,y,…,y]转换为一个3维0-1向量X=[x,x,…,x]∈{0,1}，X为D{0-1}KP问题的一个可行解或潜在解。

在NDDE 的一次迭代中，首先对种群的每个个体Y依次进行DE 中的变异操作和交叉操作得到中间个体Z=[z,z,…,z]∈[-,]；然后利用式（6）求得中间个体Z对应的0-1向量U=[u,u,…,u]∈{0,1}；最后利用式（7）选择X和Z中适应度最好的个体作为新一代种群中的第个个体（仍记为Y）。重复上述过程，直到种群的所有个体都完成以上操作为止。

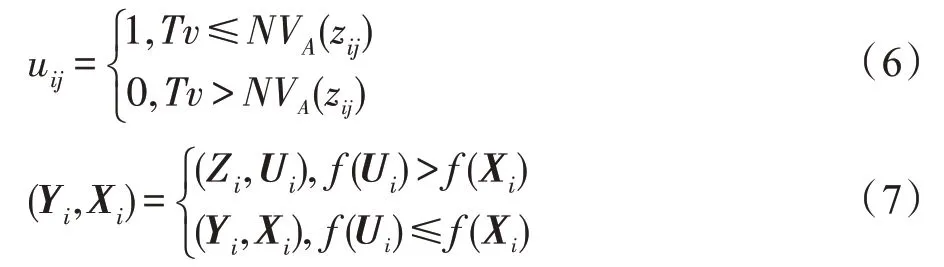
其中，NV(z)表示利用转换函数NV 将z∈[-,]转换为0 到1 之间的一个实数。∈(0,1)是一个预先设定的阈值，本文设为0.2。

2.3 利用NDDE 求解D{0-1}KP

记“[0,1,…,3-1]←（{p/w|p∈,w∈,0 ≤≤3-1}）”表示将3个物品的价值重量系数比p/w(0 ≤≤3-1)由大到小依次存入数组[0,1,…,3-1]中。记=(,,…,)∈{0,1}是种群()中最好个体对应的最好解，是算法NDDE 的迭代次数，为种群规模；∈(0,1) 为DE 交叉因子；∈(0,1)为DE 缩放因子；()是[1,]上的一个随机正整数。则基于NDDE 求解D{0-1}KP 的算法伪代码描述如算法1 所示。

NDDE for D{0-1}KP

输入：D{0-1}KP的一个实例；参数、、、、和。

输出：D{0-1}KP实例的最好解和最好值()。

1.[0,1,…,3-1]←QuickSort({p/w|p∈,w∈,0 ≤

≤3-1})；

2.随机产生初始种群(0)={Y=[y,y,…,y]|y∈[-,],1 ≤≤,0 ≤≤3-1}；

3.for←1 todo

4.for←0 to 3-1 do

5.if≤(y) then x←1 else x←0；

6.end for

7.(X(0),(X(0)))←GROA(X(0),[0,1,…,3-1])；

8.end for

9.根据(X(0))(1 ≤≤)确定种群(0)中当前最好解

10.for←1 todo

11.for←1 todo

12. for←0 to 3-1 do

13. if(＜or=())then z←y+*(y-y)else z←y；

14. if≤(z) then u←1 else u←0；

15. end for

16. (U,(U))←GROA(U(),[0,1,…,3-1])；

17. if(U)＜(X) then Y←Zand X←U；18.end for

19.根据(X)(1 ≤≤)确定当前最好解；

20.end for

21.return (,()).

在算法1 中，步骤1 利用快速排序QuickSort实现，其时间复杂度为(lb)；步骤2 的时间复杂度为(×(3-1))；步骤3～8的时间复杂度为(×(3-1))；步骤10～20 的时间复杂度为××(3-1)，因此NDDE求解D{0-1}KP的时间复杂度为(lb)+(×(3-1))+××(3-1)，当、是关于的多项式时，算法1为具有多项式时间复杂度的演化算法。

3 计算结果与分析

所有的计算均在配置为AMD Ryzen 3 2200G @3.50 GHz 和8 GB RAM 的微型计算机上进行。操作系统为Microsoft Windows 10（企业版）。利用C 语言进行编程，编译环境为Code:Blocks。使用Python 在编译环境JetBrains PyCharm 下绘制曲线图、折线图和直方图。

3.1 4 类D{0-1}KP 实例

所使用的4类D{0-1}KP实例分别为：第一类不相关D{0-1}KP 实例（uncorrelated instances of D{0-1}KP，UDKP），编号为UDKP1～UDKP10；第二类为弱相关D{0-1}KP 实例（weakly correlated instances of D{0-1}KP，WDKP），编号为WDKP1～WDKP10；第三类为强相关D{0-1}KP实例（strongly correlated instances ofD{0-1}KP，SDKP），编号为SDKP1～SDKP10；第四类为逆相关D{0-1}KP实例（inverse correlated instances of D{0-1}KP，IDKP），编号为IDKP1～IDKP10。所有D{0-1}KP实例的详细信息都可以在DOI获得（https://doi.org/10.11897/SP.J1016.02614）。

3.2 参数检验

在NDDE 中，∈(0,1)为一个预先设定的阈值，它与传递函数将算法中实向量个体转换为0 或1 的概率有关。为交叉因子，为缩放因子，[-,]为个体对应的实向量的取值空间。为了使算法NDDE 求解D{0-1}KP 问题的性能达到最佳，本文利用Kruskal-Wallis 秩和检验确定NDDE 中参数、和的合理取值。下面以参数为例，分别设置=0.1,0.2,0.3,0.4 和0.5，本文选择了40 个D{0-1}KP实例中=500（为项目个数）的4 个不同类型的代表实例UDKP5、WDKP5、SDKP5 和IDKP5。在秩和检验过程中对每个实例在取5 个不同值时独立计算30 次，种群大小设=50，迭代次数=3。

表2 中列出了Kruskal-Wallis 检验的结果，指标表示取值对计算结果的影响情况，当≥0.05 时表示取值对实验结果影响较小，否则表示取值对实验结果影响较大。秩和检验对应的盒图见图2，其中横坐标表示参数的五种不同取值，纵坐标表示NDDE 求得的最好值。

表2 秩和检验结果Table 2 Results of Kruskal-Wallis test

从表2 中可以看出：在利用NDDE 求解4 个实例时，的值远远小于0.05，这说明参数取值对于求解结果影响非常明显。从图2 中可以看出，当参数取值为0.2 时，NDDE 求解=500 的D{0-1}KP 实例的求解性能最好。

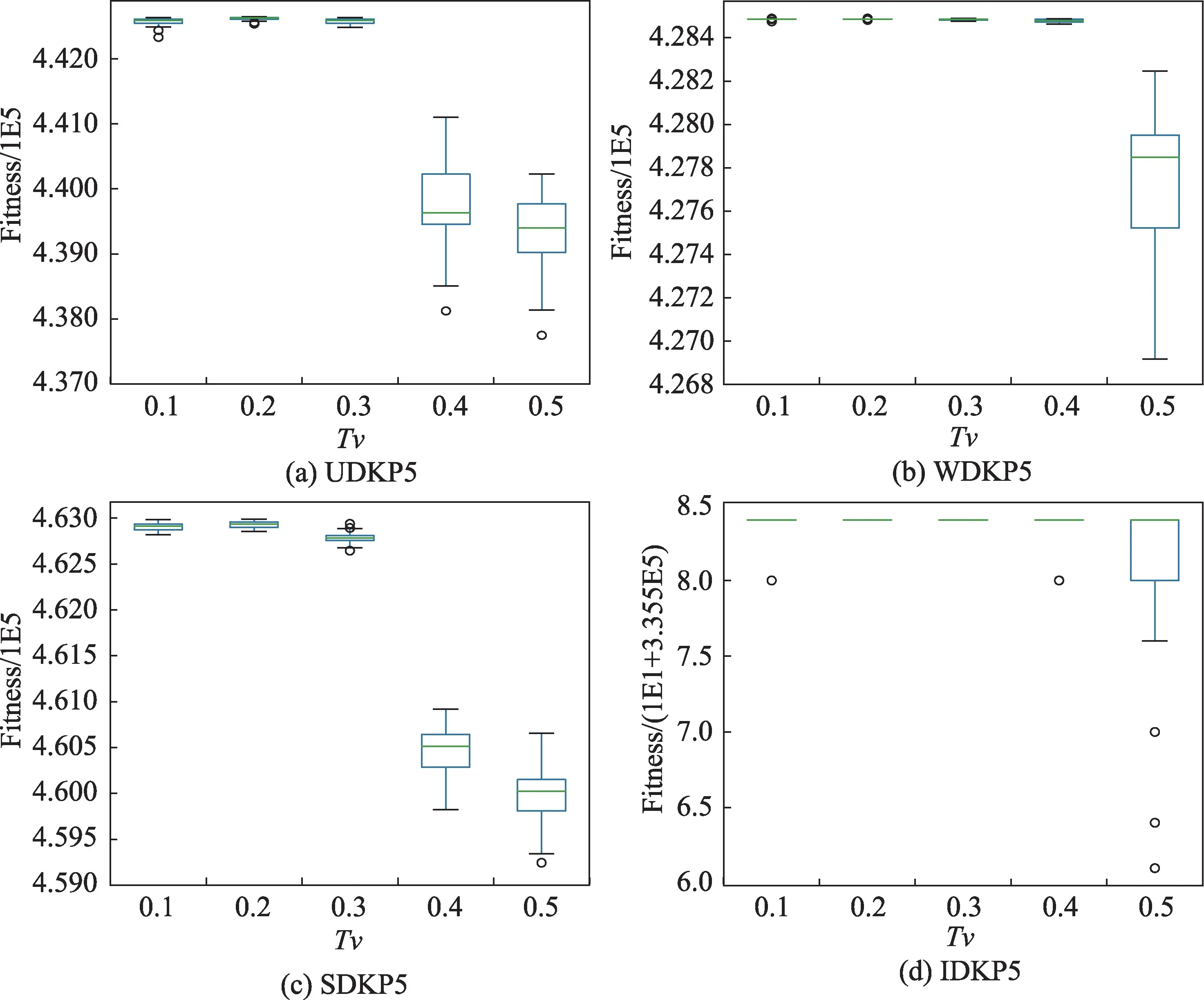
图2 UDKP5、WDKP5、SDKP5 和IDKP5 实例的盒图Fig.2 Boxplots of instances UDKP5,WDKP5,SDKP5 and IDKP5

综上，通过利用NDDE 求解D{0-1}KP 问题中4个不同类型的实例，根据Kruskal-Wallis 秩和检验结果可以确定，NDDE 中=0.5 是最佳的。NDDE 中交叉因子和缩放因子均类似于上述方法确定其最优取值。

3.3 计算结果与分析

本节中，对NDDE、GTOA、RTEA、HTLBO2、FirEGA和SecEGA求解D{0-1}KP 的计算结果进行比较和分析，在表3 中给出了上述7 个算法的具体参数设置。其中为种群规模；为迭代次数；为各算法对每个D{0-1}KP 实例独立计算次数。在NDDE 中，为交叉因子，为缩放因子，[-,]为个体对应的实向量的取值空间。在GTOA 和RTEA 中，为变异概率。在DWOA 中，是一个定义螺旋形状的常数。在HTLBO2 中，为保留因子，为影响因子。在FirEGA 和SecEGA 中，为交叉概率，为变异概率。

表3 算法的参数设置Table 3 Setting of algorithm parameters

记、、和分别为各算法在30次独立计算中得到的结果的最好值、最差值、平均值和标准差；表示实例可以求到的最优值。在表4～表7 中给出了各算法求解4 类D{0-1}KP 实例的计算结果，其中表现最好的算法用加粗标示，并根据表4～表7 中的计算结果比较了NDDE、GTOA、RTEA、HTLBO2、DWOA、FirEGA 和SecEGA 7 个算法求解D{0-1}KP 性能的优劣。

从表4 中可以看出：对于UDKP 类实例，NDDE对于6 个实例UDKP1～UDKP6 均能求得最优值，对于4 个大规模实例UDKP7～UDKP10 尽管不能求得最优值，但、和3 个指标均优于其他6 个算法。GTOA 和RTEA 的求解性能仅次于NDDE，可以求得3 个小规模实例UDKP1～UDKP3 的最优值，但是对于大规模实例的计算结果不尽人意。其他4 个算法对于UDKP 实例的计算结果较差，均不能求解任一实例的最优值。

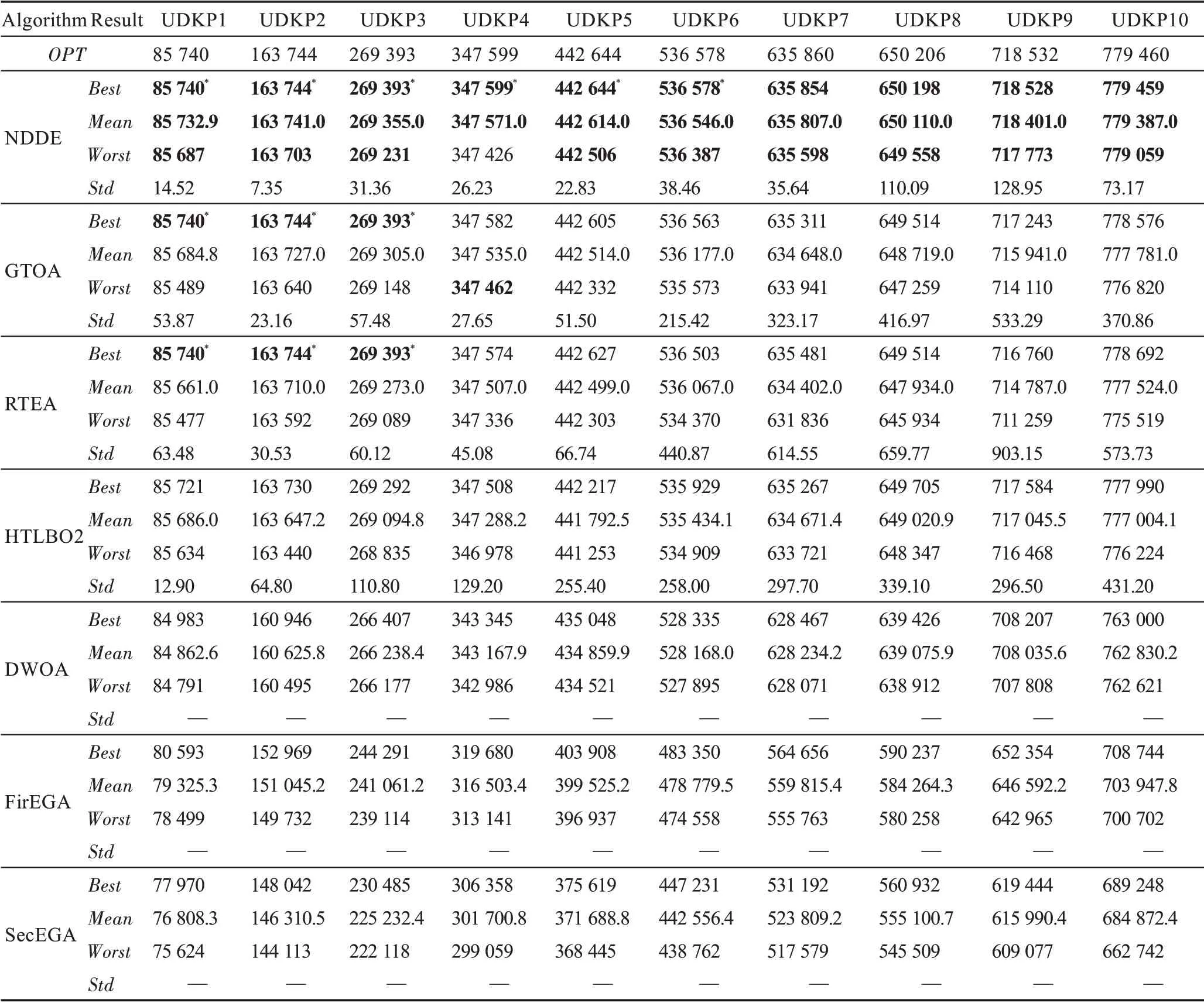
表4 NDDE 和其他算法求解UDKP 类实例的计算结果Table 4 Calculation results by NDDE and other algorithms for UDKP instances

从表5 中可以看出：对于WDKP 类实例，除实例WDKP8 以外，对于其他9 个实例均能求得最优值，求精精度远远高于其他6 个算法。GTOA 可以求得5 个实例的最优值，其求解性能仅次于NDDE。RTEA 对于小规模实例的计算结果较好，对于大规模实例的求解精度变差。4 个算法HTLBO2、DWOA、FirEGA和SecEGA 的求解性能依然和其他算法有一定差距。

表5 NDDE 和其他算法求解WDKP 类实例的计算结果Table 5 Calculation results by NDDE and other algorithms for WDKP instances

表5 （续）

从表6 中可以看出：对于SDKP 类实例，NDDE 对于实例SDKP1 和SDKP4 的计算结果较差，对于其他实例而言，等指标均优于其他算法。GTOA 对于小规模实例的计算结果具有一定竞争力，但是对于大规模实例的计算结果较差。RTEA、HTLBO2 和DWOA 等5 个算法对于SDKP 类实例的求解性能不能令人满意。

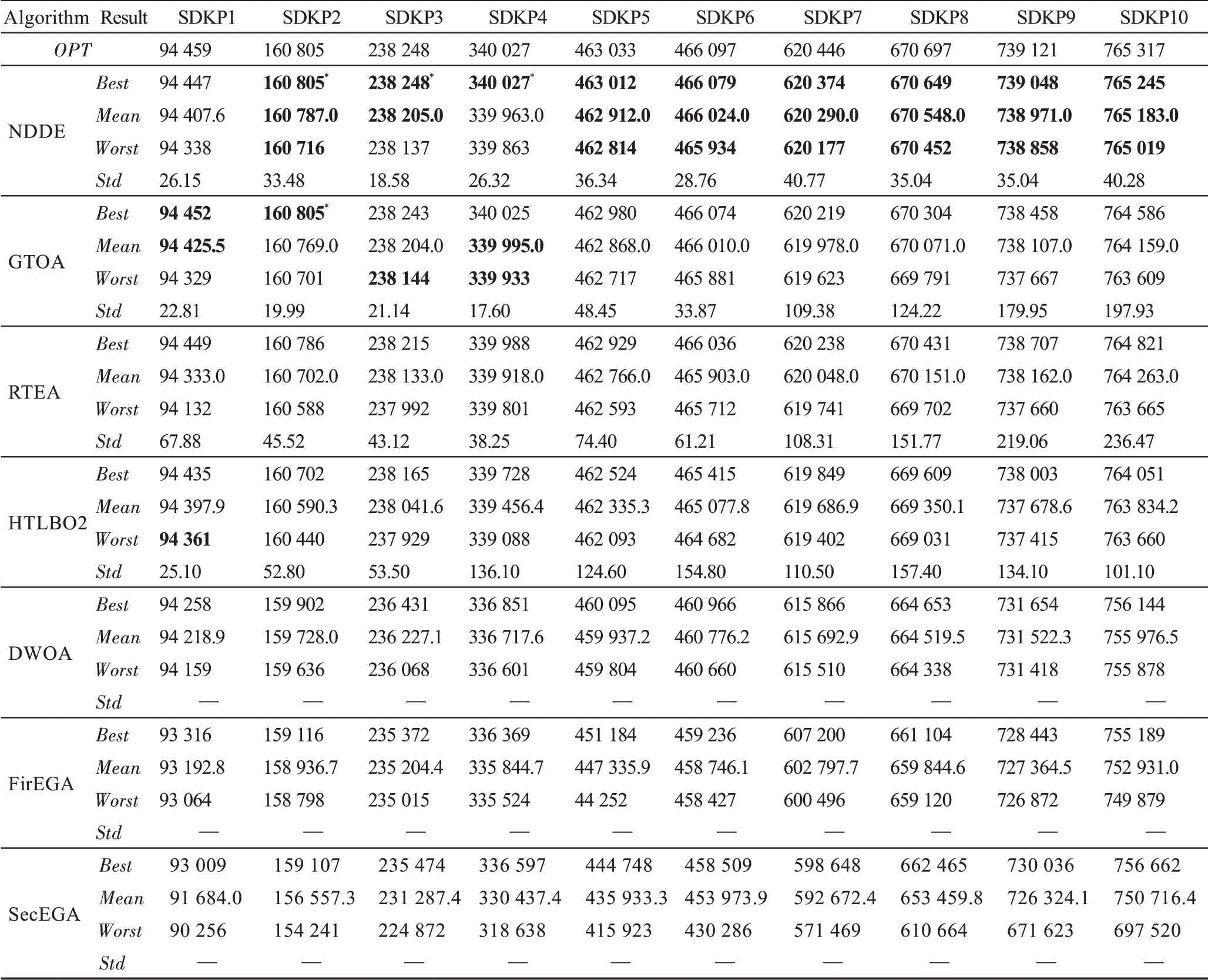
表6 NDDE 和其他算法求解SDKP 类实例的计算结果Table 6 Calculation results by NDDE and other algorithms for SDKP instances

从表7 中可以看出：对于IDKP 类实例，NDDE 不仅可以求得所有实例的最优值，而且其值远远高于其他算法，鲁棒性更佳。其次求解性能较好的是HTLBO2 和GTOA，分别有6 个和5 个实例可以求得最优值。RTEA 和DWOA 在求解小规模实例时也获得了较好的计算结果。FirEGA 和SecEGA 的总体求解性能最差。

表7 NDDE 和其他算法求解IDKP 类实例的计算结果Table 7 Calculation results by NDDE and other algorithms for IDKP instances

总体来说，对于40 个D{0-1}KP 实例，NDDE 有28 个实例可以求得最优值，求得最优值数量至少为其他算法的两倍。从来看，除SDKP1 实例外，NDDE 对于其他39 个D{0-1}KP 实例求得的均优于其他算法；从来看，除SDKP1 和SDKP4 实例外，NDDE求得的值更优。综上所述，从、和3 个指标可以说明，对于D{0-1}KP 问题，NDDE远比GTOA、RTEA、HTLBO2、DWOA、FirEGA 和SecEGA 的求解性能优，不仅求解精度更高，且稳定性更佳。

为了更直观地比较各算法的平均性能和稳定性，在图3 中给出了NDDE、GTOA、RTEA 和HTLBO2 的拟合曲线。在图4中给出了NDDE、GTOA、RTEA和HTLBO2 的对应的直方图。由于DWOA、FirEGA 和SecEGA 计算结果较差，在图3 和图4 中没有给出三种算法的拟合曲线和对应的直方图。其中为最优值与平均值之间的相对差值，见式（8）。拟合曲线越接近横轴，算法的平均性能越好。根据拟合曲线和直方图对NDDE、GTOA、RTEA 和HTLBO2 进一步进行比较。

图4 4 类D{0-1}KP 实例的Std 直方图Fig.4 Std histogram of 4 types of D{0-1}KP instances

从图3（a）可以看出：对于第一类UDKP 实例，NDDE 的拟合曲线始终是与轴趋于重合的，且不大于0.050，明显优于其他3 个算法。GTOA 在求解实例UDKP8、UDKP9 的结果较差，对于其他实例的计算结果优于RTEA 和HTLBO2；RTEA 在求解实例UDKP1，UDKP7～UDKP9 的结果较差，对其他实例的计算结果较好；HTLBO2 在求解实例UDKP1，UDKP7～UDKP9的结果较好，而对于其他实例的计算结果要差于其他算法。

从图3（b）可以看出：对于第二类WDKP 实例，NDDE 的值除实例WDKP1 的计算结果大于0.010 外，对于其他实例的值均小于0.005，明显优于其他3 个算法；其次是GTOA 和RTEA，对于第二类WDKP 实例的值均小于0.020；HTLBO2 的计算结果最差，除实例WDKP1 外，对于其他实例的值均大于0.020。

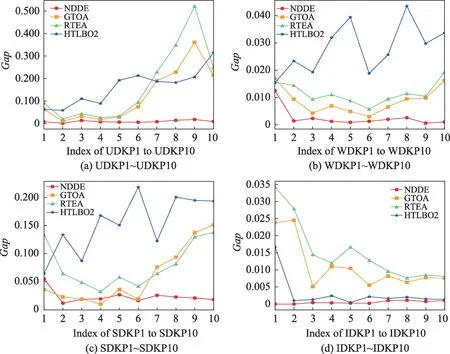
图3 4 类D{0-1}KP 实例的Gap 曲线Fig.3 Gap curves of 4 types of D{0-1}KP instances

从图3（c）可以看出：对于第三类SDKP 实例，NDDE 在求解实例SDKP1 和SDKP4 的结果较差，对于其他实例的计算结果均优于其他3个算法。GTOA在求解实例SDKP7～SDKP10 的结果较差，对于其他实例的计算结果均优于RTEA 和HTLBO2，由此可见，GTOA 不适合求解SDKP 类实例中的大规模实例。HTLBO2 求解实例SDKP1 的结果较好，而对于其他实例的计算结果较差。

从图3（d）可以看出：对于第四类IDKP实例，NDDE的拟合曲线始终是与轴趋于重合的，明显优于其他3 个算法。其次是HTLBO2，与前三类实例不同，HTLBO2 的计算结果较好，优于GTOA 和RTEA。RTEA在求解第四类IDKP实例的计算结果最差。

从图4 中可以看出，对于4 类D{0-1}KP 实例，NDDE 的算法稳定性总体来说比GTOA、RTEA、HTLBO2、FirEGA 和SecEGA 的均优；虽然对于实例SDKP1、SDKP2、SDKP4 和IDKP6，NDDE 的稳定性较差，但是对于其他36 个实例，NDDE 的稳定性明显要比其他算法的优。

综上所述，对于D{0-1}KP问题，NDDE比GTOA、RTEA、HTLBO2、FirEGA 和SecEGA 的求解结果更优，算法的稳定性更佳。因此，NDDE 是一种非常适于求解D{0-1}KP 的高效演化算法。

4 结束语

本文首先介绍了四种S 型转换函数和四种V 型转换函数，然后提出了一种新V 型转换函数（NV）。在此基础上，提出了一种基于NV 的离散差分演化算法（NDDE）。为了验证NDDE 的求解性能，本文通过求解4 类大规模D{0-1}KP 实例来证明算法的探索能力和开发能力，通过与已有算法的计算结果比较表明：NDDE 比GTOA、RTEA、HTLBO2、FirEGA 和SecEGA的求解结果更优，算法的稳定性更佳，是求解D{0-1}KP 的一个高效算法。

显而易见，本文提出的基于新V 型转换函数的离散差分演化算法求解D{0-1}KP 是非常成功的。因此在未来研究中，将探索新V 型转换函数对其他算法的影响，如灰狼优化算法（grey wolf optimizer，GWO）和鲸鱼优化算法（whale optimization algorithm，WOA）等。此外，由于设施选址问题（facility location problem，FLP）和集合覆盖问题（set coverage problem，SCP）等类似于D{0-1}KP，它们可行解中0 和1 概率分布也是不均匀的，因此将进一步考虑利用NDDE 求解FLP和SCP。