小学生数学解题心理障碍与矫正策略探析

童伟强

（华安县高车中心小学，福建 华安 363800）

小学数学具有工具性与育人性双重功能。然而，在解题素养、解题能力的培养过程中，许多教师都高度重视解题通用通法、奇招妙法的工具性研究，严重忽视影响解题内部因素、外部因素的育人性探索。这不但重踏各种知识型、记忆型的解题途径，而且阻碍创造型、开拓型的解题道路的开发，甚至诱发了许多解题心理障碍。解题是一种训练的手段，又是一种高级的活动，是蕴含多个环节的复杂过程。因此，站在心理学的角度对数学解题过程分析具有重要的价值。以下结合数学解题心理障碍的现状分析，提出一些典型的矫正策略。

一、解题心理障碍的内部影响因素

解题心理障碍，是指学生解题思维活动过程受到思维规律诸多因素（特别是思维的消极因素）的影响和各种心理因素的干扰，对促成自身身心发展正常因素的接收进行堵截，产生数学解题的误导、抑制和制约作用。解题心理障碍除外部因素影响外，更主要的是内部因素影响，主要表现为惰性心理诱发的情感过程障碍，惯性心理引起的意志过程障碍，断性心理导致的认知过程障碍。

（一）惰性心理诱发的情感过程障碍

惰性心理指的是因长期形成的松散、懒惰的坏习惯，害怕艰苦、需要毅力的脑力劳动，面对难于逾越的困难，丧失前进的勇气和信心，表现出一种情感薄弱的心理缺陷。情感过程是客观事物与认识主体之间的一种关系的态度的体验，是在认识基础上产生和形成的；反过来，它又影响着认识过程的发生发展。惰性心理来源于学生长期模仿教材例题的解题思路。由于常出现解题错误现象，久而久之，诱发对解答这种题型的厌恶、憎恨的情感，甚至产生畏惧感，严重阻碍分析与综合思维、逻辑推理思维的发展。

（二）惯性心理引起的意志过程障碍

惯性心理是指由于先前的活动而造成的心理准备状态，使人以比较固定的方式去认知事物或作出行为反应，即按固定的思路（思维顺序、固定方法、套用规律）去思考问题，对新环境的适应能力较差，表现出一种无法根据目标调节支配自己行动的意志心理缺陷。意志过程是自觉地确定目标，并根据目标支配自己的行动，克服各种内部和外部障碍、达到目标的过程。意志过程可分为采取决定阶段和执行决定阶段。惯性心理来源于长期采用固有的解题思维模式，不愿对现有的理论依据和逻辑关系进行精心推敲。久而久之，无法突破思维惯性，限制甚至阻碍思维的发展，引起意志过程障碍，无法执行决定解题阶段。

（三）断性心理导致的认知过程障碍

断性心理是指新知识与已有的经验相脱离，致使思维不能贯通，或者是已学的知识不能在大脑中再现，致使知识结构断层、思维断层，表现出一种束缚理解、难以迁移、盲目推广的认知心理缺陷。认知过程是人们认识事物的心理过程。这种认知按照由低级到高级、由简单到复杂的过程发展，可分为初级认知（感觉与知觉）、中级认知（记忆与表征）、高级认知（想象与思维）。断性心理来源于学生情绪过度的焦虑，冲淡学习的记忆，产生暂时的遗忘。学生在解题过程中，解题思维常受梗阻，久而久之，产生焦虑的情绪，无法发展高级认知（想象、推理）思维，从而导致严重的思维认知过程障碍。

二、基于解题心理障碍视角的心理矫正策略

数学解题是训练学生“基础知识和基本技能、抽象思维和推理能力、创新意识和实践能力、情感态度与价值观”的数学素养的综合体现。学生在解题的过程中，不仅会受知识想象力、逻辑思维能力和创造能力水平等智力因素的影响，而且会受到惰性、惯性、断性等心理因素的干扰。因此，关注影响学生数学解题过程中的各种心理干扰因素，培养学生稳定健全的心理品质，具有现实价值。教师可依据动态性原则、情境性原则、结构性原则，协助学生对自己的数学解题心理障碍进行矫正。

（一）动态性原则，克服惰性心理

动态性原则是指研究的对象正处于从不成熟到成熟的运动变化过程中，不能用静态的孤立的观念来对待。动态变化既是拓宽解题思维的重要途径，又是引起注意、培养兴趣的重要载体，有利于克服解题惰性心理。［1］小学教材的例题、练习题（条件、问题、关键句）中蕴含着丰富多彩的动态点，可依据动态性原则进行挖掘。

例题1 选择一个你喜欢的条件填在横线上，并解答（提示：先画出线段图、找出对应分率，再解答）

学校五月份用电600 千瓦/时，_______________，六月份用电多少千瓦/时？

A.六月份比五月份多用电20% B.六月份比五月份少用电20% C.五月份比六月份少用电20% D.五月份比六月份多用电20%

解题思维过程：如选择C.五月份比六月份少用电20%，把六月份看作“1”，通过画图（图略），可以找出“五月份用电量相当于六月份的（1-20%）”，已知五月份用电量600 千瓦时，可求六月用电量：600÷（1-20%）=625 千瓦/时。

这样设计习题，体现课程标准“重结果，更重过程”的理念，更重要的是引导学生经历解题的思维过程，避免不加思考，机械套用教材例题的解题思路。经常进行这样开放性、结构性、过程性的解题思维训练，有利于帮助学生逐渐矫正惰性心理，克服情感过程障碍，并养成良好的解题思维习惯。

（二）情境性原则，打破惯性心理

情境性原则是指人的心理活动往往会随着情境的不同而不断地发生变化。在研究主体的心理活动中，必须结合当时当地的实际情况加以分析，才能保证结果的客观性，不能用固定不变的一个模式去套一种心理现象。教师需引导学生打破固有的解题思维模式，设置具有认知冲突的挑战性题目，帮助学生获得成功体验，逐渐矫正惯性心理，克服意志过程障碍。

例题2 如图1，两个相同的直角三角形，部分重叠放在一起，求阴影部分的面积（单位：厘米）。

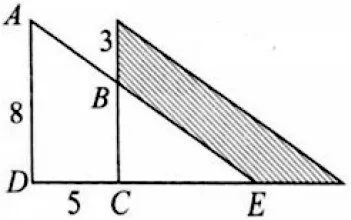
图1

解题思维过程：图中阴影部分是一块梯形，按照常规思维模式，求不出梯形面积，因为图中梯形的上底、下底与高都是未知量。必须激励学生打破思维惯性，另辟解题途径：因为阴影部分面积+三角形BCE=梯形ABCD+三角形BCE=两个相同直角三角形，所以阴影部分面积=梯形ABCD 面积，由此可求出梯形面积：［（8-3）+8）］×5÷2=32.5平方厘米。

（三）结构性原则，化解断性心理

结构性是指在寻找心理活动规律过程中，在探讨事物的因果关系时，不能认为一果只有一个因，或一个因只有一个果，而应该从一因多果、一果多因的角度去分析因变量与自变量之间的两种复杂的关系。［2］教师要帮助学生调整思维角度，转化解题思路，设置结论开放的题目，促进学生综合能力、逻辑推理能力的提升，化解断性心理，消除解题认知障碍。

例题3 ①小敏家8 月份用水27 立方米，比计划多用水1/8，__________________？（先补充问题，再列式计算）

②选择一个你喜欢的问题，并解答。

施工队修一段长2400 米的公路，第一个月修了全长的25%，第二个月修了全长的3/8，____________？

A.还剩下多少米未修？B.第二天比第一天多修多少米？C.两天共修多少米？D.第一天比第二天少修多少米？

解题思维过程：例①中，提出实际比计划多用水多少吨？此题“1”的量未知并且不是所求问题，则可先求“1”的量，再求所求问题。因此，计划用水：27÷（1+1/8）=24 吨，多用水：27-24=3 吨。例②中，若选择B.第二天比第一天多修多少米？依题意可知，公路全长为“1”，第二天比第一天多修的长度占全长的（3/8-25%）。已知公路全长2400 米，则第二天比第一天多修的长度：2400×（3/8-25%）=300 米。