回顾梳理 建构发现 深化应用
——“三度”提升复习课品质
林冰
(台江区教师进修学校,福建 福州 350004)
当前,许多教师对复习课的认识存在明显的“误区”:一是“炒冷饭”,简单罗列单元知识点后,开始重复性的讲解;二是囿于旧有的教学传统,复习面狭窄,就题讲题,缺乏新意;三是复习课变成练习讲评课,机械刷题,训练浅表性的应试技巧。这样的复习课,教师教得苦,学生学得累,教学效果差。针对以上误区,结合期末复习课例,笔者提出如下几点提升复习课品质的建议。
一、回顾梳理,提炼知识精度
杜威说过:“好的教学必须能唤起儿童的思维。”教学设计的突破口在于针对学习主题和学生学习特征创设问题情境,提出引发学生深度思考的关键问题,进而组织学生围绕关键问题进行深度探究。[1]复习课的设计,首先是对所学知识的回顾整理。在传统的复习课中,教师提问:“这个单元学习了哪些知识?”学生开始三三两两的罗列,大多泛泛而谈或蜻蜓点水,甚至南辕北辙,看上去是发挥了学生的主体性,但无法快速指向复习内容的本质,最终还是演变成教师的“一言谈”。究其原因,主要是小学生以形象思维为主,需要精准定位,教师要创设具体直观的问题情境,帮助学生归纳梳理零散知识,触及知识的核心。
以二年级上册“长度单元”“角的初步认识”“观察物体(一)”三个单元的总复习为例(简称“总复习一”)。这几个单元知识点比较零散,在教学设计中,教师以“1 个点的神奇之旅”引入,联结本学期“图形与几何”领域的所有核心内容。复习课伊始,用课件动画演示“点动成线”,学生直观感受,重温线段是“直直的”“可测量的”两个基本特征,同时渗透“两点确定一条线段”的思想。接着,在线段下面出示1 厘米的方形纸条,请学生估一估这条线段有多长,培养量感。学生用直尺验证时,移动直尺并思考:“为什么测量起点不同,得到的测量结果却相同?”突出测量的本质“含有几个1 厘米,就是几厘米”。在复习“角的初步认识”单元时,仍然从这个点出发,引出两条射线,呈现角的动态变化过程。学生基于观察到的表象,马上整理出关于角的特征、角的大小、角的分类等知识点。最后演示“线动成面”,呈现一个正方形,引发学生思考:“如果看到的立体图形的一个面是正方形,这个立体图形可能是学过的哪个图形?”在判断推理中,复习“三视图”的相关知识。通过“点-线-面-体”的情境串设置,紧扣复习内容的主线,在回顾梳理中,聚焦核心知识,实现少量主题的深度覆盖,达到举一反三的效果。
二、建构发现,拓宽知识“广度”
建构主义认为,学习是知识建构。教师要思考如何优化学习环境中蕴涵的丰富资源以便为学习者提供丰富的“给养”,支持学习者对知识的积极建构。[2]复习课除了归纳梳理,同样承担着对知识重组建构的任务,需要教师精心组织能引发学生深度探究的活动,设计具有挑战性和趣味性的学习任务,围绕探究活动中的关键性问题,给予学生足够的时间和空间去自主探索和操作,实现对知识广度的拓展,才能真正锻炼思维,发展能力。
以一年级上册“复习加减法”为例,教材中出现121 个格子,涵盖20 以内的加法所有算式(如图1)。本节总复习课的教学目标是引导学生发现表格中横行、竖行和斜行的排列规律,了解加法表的建构。为实现目标定位,教师首先出示一张被全部遮挡的表格,请学生“揭开”任意一个格子,显示如“4+8”。
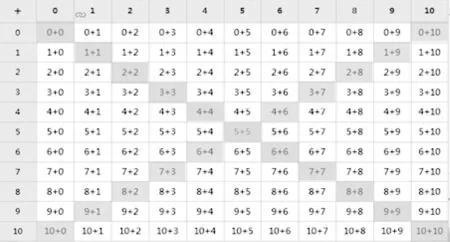
图1 20 以内加法算式建构表
师:我不用看,就知道在它左边的算式是多少?4+7。(说完后揭示答案)我还知道它上边的算式应该是3+8。(再次验证)那么,它下边的算式是——
生1:5+8。(点开检验)
生2:我知道右边算式是4+9。
师:能把这一行和这一列的算式都猜出来吗?(随着学生的回答,教师点开行与列下面隐藏的算式)
师:观察这一行(列),你发现了什么?
经过交流讨论,学生找到横行与竖列排列的规律,发现表格中第一行与第一列就是加法中两个加数所在的位置,了解了表格的“基本构造”。
师:能从表格中找到‘6+5’这个算式吗?
师:(指着任意一个格子)这个格子下面隐藏的应该是哪个算式?说说你的想法。
教师先从局部入手,从一个算式引出相关联的多个算式,再延伸到一组算式,巧妙地解构了加法表的排列规律。在若干个核心问题的引导下,学生边观察边思考,从部分到整体,探究了加法表的构造,顺藤摸瓜,运用规律,解决问题,最初的“直觉判断”转化成了“科学推理”。原本抽象枯燥的百格图,在教师的精心设计下,变得生动有趣,富有新意,激发了学生探究的欲望。因此,必须赋予复习课新的内涵,在知识的建构、发现中,培养学生数学核心素养。
三、深化应用,挖掘知识“深度”
落实数学核心素养的基本途径就是要建构深度学习的课堂。所谓深度学习就是指在教师引领下,学生围绕着具有挑战性的学习主题,全身心积极参与、体验成功、获得发展的有意义的学习过程。[3]复习课的设计要从学习任务出发,教师要提供必要的方法、工具、策略,激发学生学习的主动性,体现问题解决策略的多样性,渗透学习方法和过程的指导,在交流探讨、行动实践中,最终实现对问题的深入理解。
在上文提到的“复习加减法”一课中,当121 道20以内的加法算式全部显示出来后,引导学生进一步观察发现两个斜行的“秘密”,渗透“和的变化规律”与“加法交换律”。学生在观察比较中,读懂运算的“理”。在另一节“总复习一”课例中,设计了两道提升性的练习:一道是对复合线段的分解和组合(如图2),让学生初步具有拼组的眼光。另一道是教材原题的变式,在直角梯形中添一条线段增加2 个直角、3 个直角、4 个直角,最后对比呈现5 种位置的“辅助线”(如图3)。这样多角度的解题策略,有利于提升学生的发散性思维。在课的结尾用数学画板演示“点动成线、线动成面、面动成体”,不仅串起二年级上册分散在三个单元中“图形与几何”内容的知识,更重要的是在儿童的心里播下数学的种子,这才是包裹在外显的知识中最关键的内核。
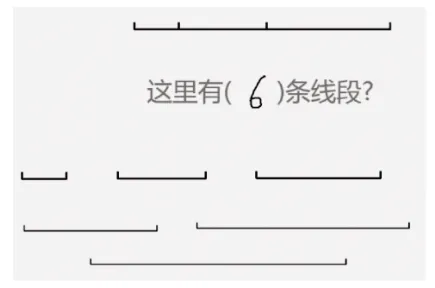
图2
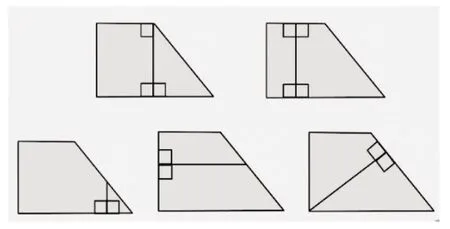
图3
复习课是挖掘知识深度的有力阵地,特别是在学生已经掌握了新知的情况下,有更加充足的时间与空间作进一步深入思考,教师要设计引发学生深度学习的问题情境,开展深度探究的学习活动,实现高阶思维的培养。

