基于天牛须搜索算法的多船避碰决策方法

刘 朝 黄立文 张 可 郝国柱

(武汉理工大学航运学院 武汉 430063)

0 引 言

在航海实践中，驾驶员通常是依靠自身经验来制定船舶的避碰决策，但当处于比较复杂的多船会遇局面时，驾驶员很难保证可以做出最优的避碰决策[1].因此，许多专家学者应用智能优化算法来研究船舶的避碰策略问题，并取得了很多的成果.文献[2]将社会情感优化算法应用到船舶转向避碰的决策中，以便求解出船舶最佳转向，但系数调节较为复杂.文献[3]基于改进的免疫粒子群算法，给出了一种求解多船会遇局面下计算最佳转向幅度的方案.文献[4]通过结合前景理论和多指标灰关联决策，建立了考虑驾驶员风险态度的避碰决策优化模型，结果表明：该模型可帮助驾驶员在不同风险偏好下选取最优避碰方案.文献[5]以船舶最近会遇距离和最近会遇时间建立碰撞危险度模型，综合考虑转向幅度和航行时间，构建了避碰决策模型，并提出了一种使用粒子群-遗传优化算法求解该决策模型的方案.然而，这些算法大多在于模拟动物的群体性活动，无法从个体中获取有效的决策，求解过程也较为繁琐.

天牛须搜索(beetle antennae search，BAS)是一种类似于遗传算法、粒子群算法、模拟退火等算法的智能优化算法[6].该算法不需要知道函数的具体形式，也不需要求解函数的梯度，就可以实现全局高效寻优.相比较粒子群算法，BAS算法仅需要一个个体，极大地降低了寻优过程的运算量.目前该算法已经被应用于机器故障诊断、电网优化调度、选址、图像修复及路径规划等多个领域，并表现出算法在解决优化问题中的有效性及优越性[7-10].本文利用船舶碰撞危险度并考虑船舶在进行避碰操作时的损失函数来确立符合航海实际的避碰决策目标函数，并利用BAS算法研究多船会遇局面下最优避碰转向幅度以及复航时间，并通过仿真实验验证该避碰决策方案.

1 船舶会遇态势的划分

海上实践表明，对会遇态势的认识不一致是造成船舶间避碰行动不协调乃至碰撞的重要原因之一[11].根据《国际海上避碰规则》对追越、对遇和交叉相遇的定义以及相关规定，以本船为中心，将他船相对于本船的方位划分为五个区域[12]，见图1.

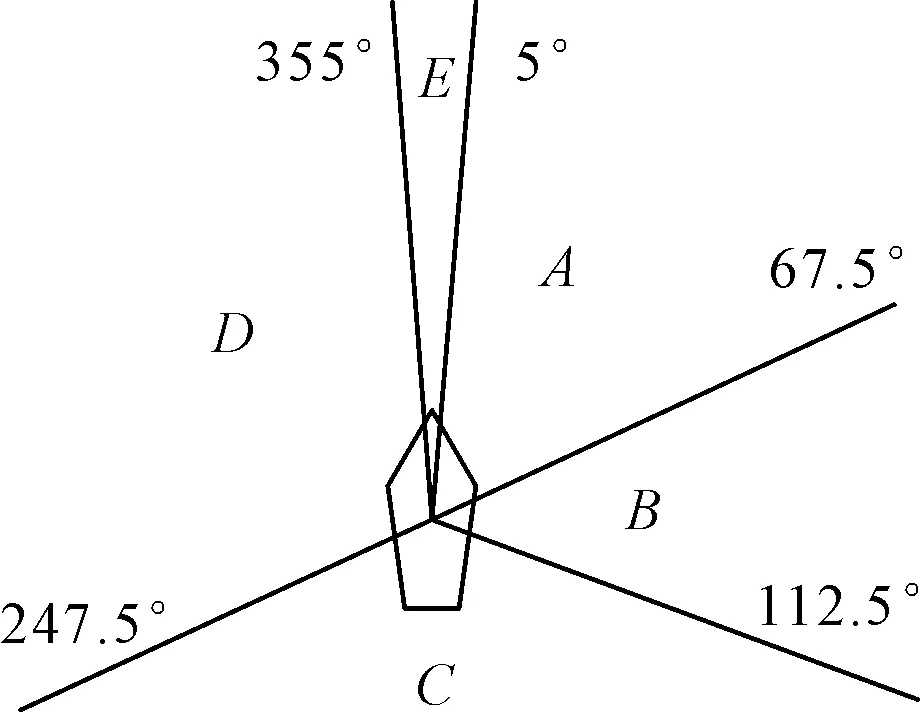
图1 船舶会遇态势划分

根据避碰规则，若互见中两船之间存在碰撞风险，对于E、A区域的来船，本船是让路船，需要进行相应的避碰操作，一般通常是进行右转向操作；若来船位于B区域，则本船为让路船，一般来说本船可以通过降低船速或者是进行左转向操作进行避碰；若来船处于C、D区域，那么本船为直航船，来船需要进行相应避碰操作.

2 船舶碰撞危险度

船舶碰撞危险度(collision risk index，ICR)是对船舶之间发生碰撞的可能大小的一个度量，其取值范围是[0,1].目前对于船舶碰撞危险度的计算模型有很多，文中以船舶之间距离(D)、船速比(K)、他船与本船之间相对方位(B)、最近会遇距离(DCPA)，以及最近会遇时间(TCPA)等五个指标为主要参数，并综合考虑航行水域状况、能见度情况、操船者技术、船舶操纵性能等因素，确定他船与本船之间的碰撞危险度[13].

设uDi、uKi、uBi、uDCPAi、uTCPAi分别为与本船会遇的目标船i各主要参数的危险隶属度，取值范围为[0,1]，i=1,2,…,n.那么本船与目标船i之间的碰撞危险度ICRi即为

ICRi=aDuDi+aKuKi+aBuBi+

aDCPAuDCPAi+aTCPAuTCPAi

(1)

式中：aD，aK，aB，aDCPA，aTCPA为五个主要参数的危险隶属度的权重，取值范围为[0,1]，且满足

aD+aK+aB+aDCPA+aTCPA=1

(2)

船舶之间的距离越小，碰撞危险度就越大.船舶之间距离的隶属度函数为

(3)

式中：D1为最晚避让距离；D2为可采取避让措施距离，由航行水域状况、能见度，以及人为因素等决定.取值为

D1=H1×H2×H3×DLA

(4)

D2=H1×H2×H3×Ri

(5)

Ri=1.7cos(Bi-19°)+

(6)

式中：H1取决于能见度；H2由航行水域状况决定；H3取决于操船者经验、技术、反应能力等人为因素，DLA为最晚施舵距离，通常取12倍的船舶长度.

(7)

式中：W为常数，这里取值为2；C为碰角(0°≤C≤180°).

(8)

(9)

式中：d1为船舶碰撞距离；d2为船舶注意距离.

(10)

d2=2d1

(11)

(12)

式中：t1为船舶碰撞时间；t2为船舶注意时间，并且

(13)

(14)

式中：vri为目标船i与本船之间相对速度.

3 基于天牛须搜索算法的多船避碰决策方法

3.1 天牛须搜索算法基本原理

天牛须搜索也被称为甲壳虫须搜索，搜索过程的简化模型见图2.

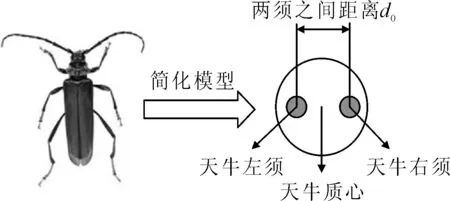
图2 天牛搜索过程简化模型

那么该简化模型的寻优策略即为

1) 天牛的左右两须应位于天牛质心的两边；

2) 天牛行动的步长step与左右两须之间的距离d0比值应该是一个固定的常数，即step=c·d0，其中c为常数.也可以理解为体型较大的天牛(两须之间的距离长)行走的步长较大，体型较小的天牛行走的步长较小.

3) 天牛每次行动之后，它的头部朝向应该是随机的.

3.2 BAS算法建模

假设要求解一个n维的空间中目标函数f的最小值，现设天牛的质心坐标为x，左须坐标为xl，右须坐标为xr，左右两须之间的距离为d0.由寻优策略(3)可知，天牛的头部朝向是随机的，所以由右须指向左须的向量的方向也是随机的，在此用随机向量dir=rands(n,1)来表示右须指向左须的向量.对其进行归一化处理，即

(15)

由此，可以得到

xl-xr=d0×dir

(16)

(17)

对于目标函数f，首先求取天牛当前位置左右两须的值，即fl=f(xl)，fr=f(xr).

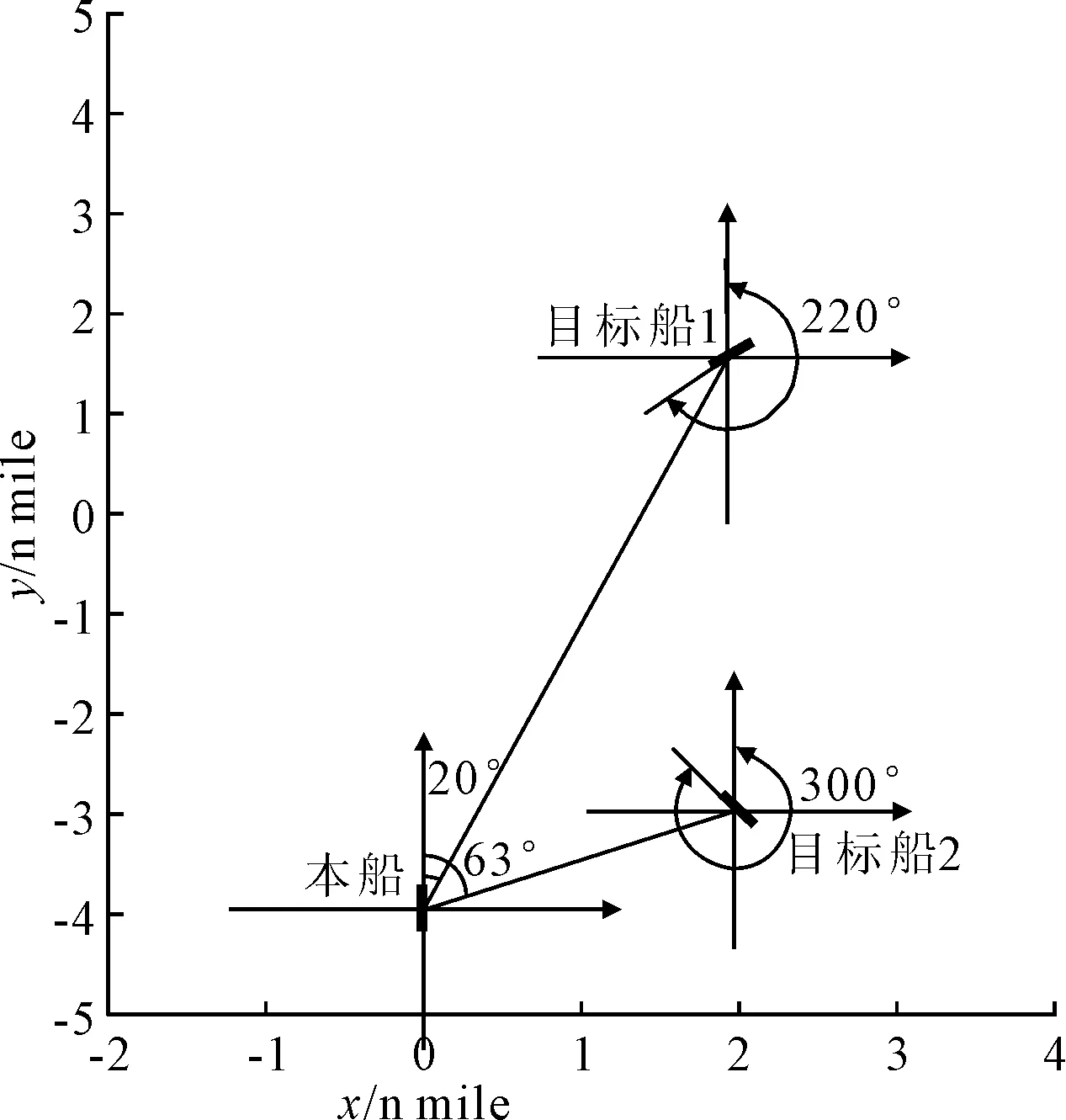
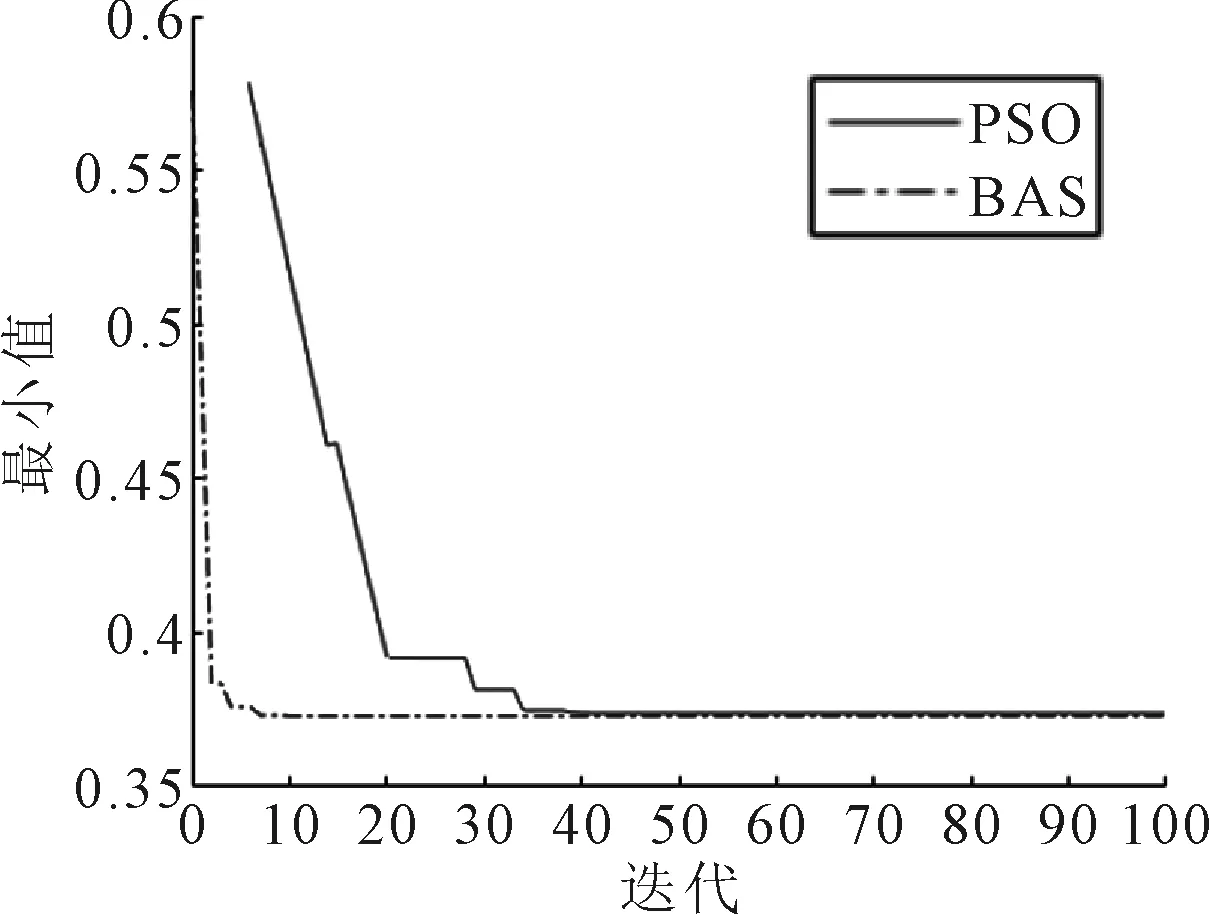
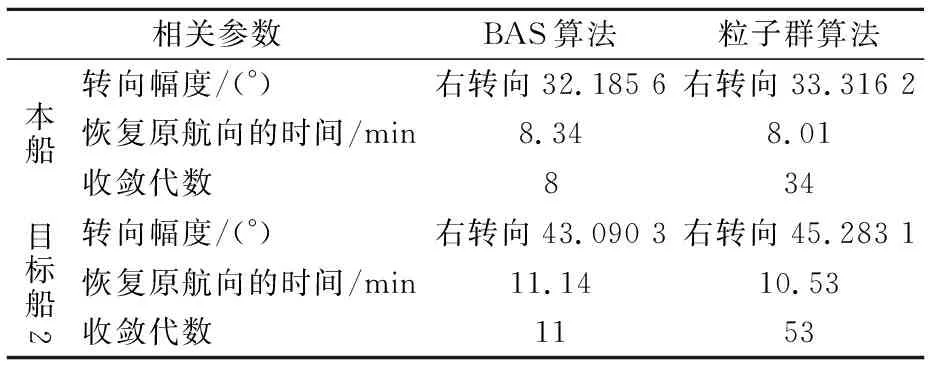
如果fl

x=x+step×dir

(18)

如果fl>fr，为了寻找目标函数的最小值，此时天牛应该朝着右须的方向飞行step的距离，即

x=x-step×dir

(19)

为了简化形式，使用符号函数sign对式(18)和(19)进行简写

x=x-step×dir×sign(fl-fr)

(20)

此外，对于天牛行动的步长，本文将使用变步长的方式代替固定步长.在每次的迭代过程中，将步长设置为step=eta·step，其中：eta∈[0,1]且接近于1，这里取eta=0.95.

3.3 避碰决策目标函数

当船舶之间存在碰撞危险时，一般来说，常用的避碰操作是采取变速、转向或者同时进行转向和变速等方式.由文献[13]可知，通常情况下，即使是处于多船避碰的局面，船舶也可以通过一次转向或者变速来实现避碰，并且转向避让是使用频率最高的一种方法，很少会同时进行转向和变速操作.所以，本文将主要研究船舶避碰操作中的转向避碰操作.

当会遇的船舶之间存在碰撞危险时，需要根据本船与他船之间的会遇态势，合理的选取转向幅度，此时应满足：

1) 转向后，应使得会遇船舶之间的碰撞危险度尽可能的减小.

2) 在满足避碰规则“大幅度”要求的前提下，转向幅度应尽可能的小，以减少资源的损耗.

3) 船舶转向后，在保证航行安全的前提下，在新航向上的航行时间要尽可能的短，以降低复航的难度.

基于以上三点，在多船会遇时，船舶的避碰决策目标函数为

minf(x)=w1f1(xi)+w2f2(xi)

(21)

式中：f1(xi)为目标船i与本船之间的碰撞危险目标函数，f2(xi)为航程损失的目标函数，w1、w2为权重系数，为了便于寻优计算，w1取0.7，w2取0.3.

碰撞危险目标函数为

(22)

式中：n为目标船个数.

航程损失的目标函数为

(23)

式中：xi为转向幅度，航程损失函数的取值范围为[0,1].同理，损失函数的值越小，转向幅度和复航时间应越短.

4 仿真分析

假设在开阔水域中能见度良好，驾驶者技术水平良好，船舶的操纵性能良好，即H1=1，H2=1，H3=1.本文以三船会遇局面为仿真对象，本船的初始位置为(0,-4)，航速为16 kn，航向为0°；目标船1的初始位置为(2,1.5)，航速为16 kn，航向为220°；目标船2的初始位置为(2,-3)，航速为17 kn，航向为300°.船舶间的初始会遇态势见图3.

图3 船舶间初始会遇态势

由船舶间的初始会遇态势，以及表1中船舶间的相关参数可知，本船与目标船1、目标船2之间的碰撞危险度都很大，存在很高的碰撞风险.根据避碰规则，此时两目标船为直航船，本船应及早采取合适的避碰行动，以降低本船与两目标船之间的碰撞风险.同时对于目标船2和目标船1来说，两船之间也存在碰撞风险，根据避碰责任，目标船2也要采取合适的避碰操作来降低与目标船1之间的碰撞风险.因此，对于图3的会遇局面，本船需要选取合适的转向幅度以降低与两目标船之间的碰撞风险；而目标船2也要找到最优的转向幅度.

表1 初始会遇船舶间相关数据

在图3的多船会遇局面中，使用BAS算法为本船规划一个合适的避碰方案，以降低碰撞风险.使用BAS算法对式(21)的目标函数进行寻优计算，同时为了避免计算结果的偶然性，对该寻优过程进行10次重复操作，每次的迭代次数均为100次，最终求得平均最优转向幅度为32.185 6°本船恢复原航向的时间约为8.34 min.即本船的最佳转向幅度是右转向32.185 6°，在该航向上航行大概8.34 min之后可以完成避碰操作.同时为了验证BAS算法的有效性，使用粒子群算法对避碰决策目标函数进行求解.算法的寻优过程见图4.

图4 本船的PSO和BAS算法迭代过程

使用BAS算法对目标船2的转向幅度进行寻优求解.在经过10次重复计算之后，得到的平均最优转向幅度为43.090 3°，恢复航向使用的时间为11.14 min.算法的迭代过程见图5.

图5 目标船2的PSO和BAS算法迭代过程

表2将BAS算法对多船会遇局面避碰策略的求解结果与粒子群算法进行了简单的对比.从表中可以看出，BAS算法的收敛速度快，求解出来的最优转向幅度比粒子群算法要小，但复航时间要稍微长一点，这与实际情况是相符合的.同时本文所用的碰撞危险度模型综合考虑了船舶的操纵性能、人为因素、航行环境等因素，使得BAS算法求得的结果也更符合航海实际.

表2 算法对比

5 结 束 语

本文通过分析船舶的会遇态势，结合避碰规则对避碰责任进行了划分，在综合考虑航行水域情况、能见度、操船者技术、船舶操纵性能等因素的基础上，使用船舶之间距离、船速比、方位角、最近会遇距离以及最近会遇时间等五个指标确定了比较符合航海实际的碰撞危险度模型，通过对避碰操作过程中转向幅度的分析，建立了避碰策略目标函数，利用BAS算法的全局搜索能力强、寻优速度快、鲁棒性强的特点，求得了多船会遇下最优避碰转向幅度以及复航时间.通过三船会遇的仿真实验，验证了算法的有效性.