城市区域交通信号控制与交通诱导协同模型研究

梅 朵 袁梦柯 郑黎黎 鄂 旭

(渤海大学信息科学与技术学院1) 锦州 121013) (吉林大学交通学院2) 长春 130012)

0 引 言

交通信号控制和交通诱导是解决城市交通拥堵的主要手段.然而单一的交通信号控制只能在时间上改变交通流的分布，单一的交通诱导只能在空间上均衡交通流，因此，交通信号控制与交通诱导协同运作才能有效缓解城市交通拥堵，保证城市交通顺畅.

Li等[1]采用仿真方法研究的VMS和交通信号控制系统协同问题.保丽霞等[2]提出的双目标协同模型.徐立群[3]提出的一体化协同模型.孙智源等[4]提出的双层规划模型.通过分析发现，交通信号控制与交通诱导的协同时机有两种情况：①通过预测交通流设计高峰时段的预先协同方案；②通过实时交通流设计拥堵发生中的协同方案[5-7].文中针对第一种情况，研究城市区域范围内的交通信号控制与交通诱导的预先协同优化，引入饱和度、有效绿灯时长、周期时长和相位差作为约束，构建了一种城市区域交通信号控制与诱导协同的一体化模型，提出了一种基于MapReduce的并行遗传算法对所提出的协同模型进行求解，并基于VISSIM仿真数据验证所提出的协同模型和求解算法的有效性和可行性.

1 问题描述

城市道路网是一个复杂的大系统，具有动态性、复杂性，也具有规律性.每天的早晚高峰时段，随着交通需求的不断增加，路网容量不能满足需求，一些脆弱的交叉口和路段首先发生交通拥堵，如果不能进行行之有效的处理，极易出现交通流量上溢，造成区域交通拥堵.为了避免发生区域交通拥堵，在日常交通信号控制的基础上，有效监控路网的实时交通流参数，如果发现某些交叉口或路段的流量变大、运行速度降低、排队长度增加，则说明该交叉口或路段发生交通拥挤，当即将形成区域交通拥堵时，启动交通控制与诱导协调方案，避免区域交通拥堵的发生.

文中所提出的交通控制与诱导协同方案的基本思想是：①从交通控制角度出发，通过不断优化拥堵路段上下游交叉口的信号配时参数，及时有效地降低路段上的交通量，避免路段上的排队长度增加；②从交通诱导角度出发，有效均衡整个路网的交通量，保证所有路段的总行程时间最小.

2 模型建立

在建模时，充分考虑了交通管理者和驾驶员的目标，以“准系统最优”的指导思想为原则，构建区域交通控制与诱导协同模型[8].文中所构建的区域交通控制与诱导协同模型的目标函数如下.

(1)

式中：a为某路段；A(i)为从某节点到以节点i的所有弧段总和；xa(t)为t时刻a上的流量；ta(t)为t时刻a上车辆的总行程时间.

一方面从交通管理者的角度出发，考虑整个交通网络的总行程时间最小，保证交通网络系统流量均衡；另一方面从驾驶员的角度出发，实时调整交通信号配时，迅速卸载路段上的流量.

2.1 行程时间的表达

行程时间由两部分构成：车辆在路段上的运行时间ta,r(t)和车辆通过交叉口的时间ta,s(t).

当路网处于畅通条件时，

ta,r(t)=Lj/ϑi

(2)

式中：Lj为路段j的长度；ϑi为时间段i内，路段j的平均速度的预测值.

当路网处于拥挤条件时，路段上会出现排队车辆，ta,r(t)等于自由流行驶时间ta,r,f(t)和拥挤行驶时间ta,r,c(t)的总和.假设驾驶员的反应时间和启动加速时间忽略不计，自由流行驶时间为

(3)

式中：Lj为路段j的长度；Lij为实时采集的排队长度；ϑi为平均速度的预测值.

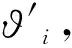
(4)

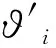
关于车辆通过交叉口的时间ta,s(t)，文中采用修正后的HCM2010进行计算求得.

2.2 约束条件

1) 饱和度 当区域路网的平均饱和度和饱和度方差都比较高的时候，表明路网中存在交通拥堵，因此路网的平均饱和度和饱和度方差应该都小于一定阈值.

(5)

(6)

(7)

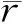
2) 有效绿灯时长 从行人过街的安全性方面考虑，交叉口所有相位的有效绿灯时长参数不得小于一个阈值e(一般e≤6 s)，交叉口所有相位的信号配时参数还应该满足以下条件.

e≤gi≤T-(m-1)e,i=1,2,…,m

(8)

式中：m为交叉口的相位数；T为路网协同区域的统一周期时长；gi为相位i的有效绿灯时长.

3) 周期时长 从驾驶员的心理承受能力方面考虑，在设计路网协同区域范围内的所有交叉口的统一周期时长时，需要满足以下条件[9].另一方面，因为频繁变换周期时长会造成交通混乱，所以路网协同区域范围内的所有交叉口的统一周期时长取各个交叉口周期时长的最大值[10].

30≤T≤200,C=max{T1,T2,…,Tn}

(9)

式中：n为协同区域内交叉口的个数；Ti为交叉口i的信号周期时长，Ti通过Webster方法获得，

(10)

(11)

式中：L为损失时间，s；Y为各个信号相位中的总流量比；yj为相位j的流量比；qd为设计交通量，pcu/h；Sd为设计饱和流量，pcu/h.

4) 相位差 在协同控制中，相位差是一个重要参数，交叉口i到j的上行相位差ψ上和交叉口j到i的下行相位差ψ下必须满足下列条件.

(12)

式中：T为协同区域范围内统一周期时长.

综上，本文构建的区域交通控制与诱导协同优化模型为

(13)

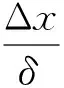
3 求解算法

3.1 染色体编码和解码

构建的协同模型包括流量[x1,…xn1]、绿灯时长[g1,…gn2]和相位差[ψ1,…ψn3]三个参数，n=n1+n2+n3为参数数目，采用二进制编码方法进行编码，其编码公式为[11]

(14)

采用二进制编码方法对参数x、g和ψ进行编码，设l1、l2和l3为编码长度，那么l1+l2+l3即为染色体的总长度，解码公式为

(15)

(16)

(17)

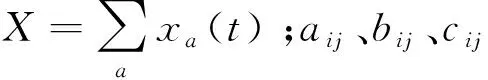
3.2 适应度函数确定

合理的适应度函数可以提高算法的效率和求解解的质量[12].基于“界限构建法”确定适应度函数为

(18)

该适应度函数可以保证遗传操作中的概率非负，也可以避免出现因函数值差距大引起的种群平均性能变弱的现象.

3.3 遗传操作算子

1) 选择操作算子 通过选择运算，选出适应度值高的个体，并遗传给下一代.文中的选择运算采用轮盘赌法，则适应度值为f(i)的个体被选择的概率为

(19)

2) 交叉和变异操作算子 交叉运算采用单点交叉法，即先确定交叉点区域，再确定交叉点，然后进行运算，生成新个体[13].变异操作尽可能地淘汰较差的个体，提高遗传算法的全局搜索能力.变异操作运算选择基本位变异法，先根据变异概率确定变异节点，然后进行基因变换，形成新个体.为尽量保存优秀个体，采用自适应交叉概率和变异概率函数确定变异点.具体函数分别为

(20)

(21)

3.4 协同模型求解

文中设计的基于MapReduce的并行遗传算法采用8台计算机搭建Hadoop并行计算平台.所设计的算法的详细步骤如下.

步骤1种群初始化 主机器对种群进行初始化，并设置相应的参数，即种群大小M、染色体长度n和进化代数N.主机器将相应的参数分配到从机器上去.

步骤2对染色体进行二进制编码 主机器在参数取值范围内随机生成种群大小的染色体，并均分成M个子种群，分配给M个从机器.

步骤3染色体解码 以子种群编号为键，以染色体为值，组成键值对.每个从机器分别调用Map函数，对所有染色体进行解码，从而得到x1,…,xn1的值.

步骤4计算信号周期 每个从机器分别调用Map函数，通过Webster法求得每个信号交叉口的周期时长.根据最大值原则，确定周期时长的最大值为公共信号周期时长T=max{T1,T2,…,Tn}.

步骤5染色体解码，得到T每个从机器分别调用Map函数，采用公式(16)和(17)对染色体的后几位进行解码，求得[g1,…,gn2]、[ψ1,…,ψn3]的值.

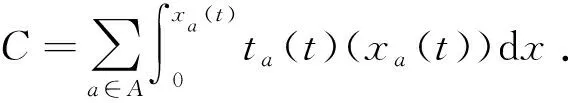
步骤7计算适应度值 每个从机器分别调用Map函数计算适应度值，并按照键的不同，对其值进行归约，得到各个小的数据集合，并将其保存到本地的HDFS中.

步骤8算法结束条件判断 通过设置最大进化代数N，来判断是否结束算法.如果达到最大进化代数，则输出最优值J,x,g,ψ,T；否则，跳到步骤10.

步骤9选择运算 主机器确定中间结果的位置，并通知Reduce函数.从机器调用Reduce函数，采用轮盘赌法从中间结果中选择适应度值较高的个体遗传给下一代.

步骤10交叉和变异运算 从机器调用Reduce函数，运用单点交叉法进行交叉运算，采用基本位变异法进行变异运算.最终得到的新一代个体存储到HDFS中，返回步骤4.

步骤11算法终止条件判断 当算法运行到最大进化代数N时，得到最优的J,x,g,ψ,T值，算法终止.

4 仿真模拟验证

以长春市新民大街-自由大路-人民大街-解放大路所构成的区域路网的交通参数数据为基础，通过VISSIM仿真软件搭建图1的区域路网.

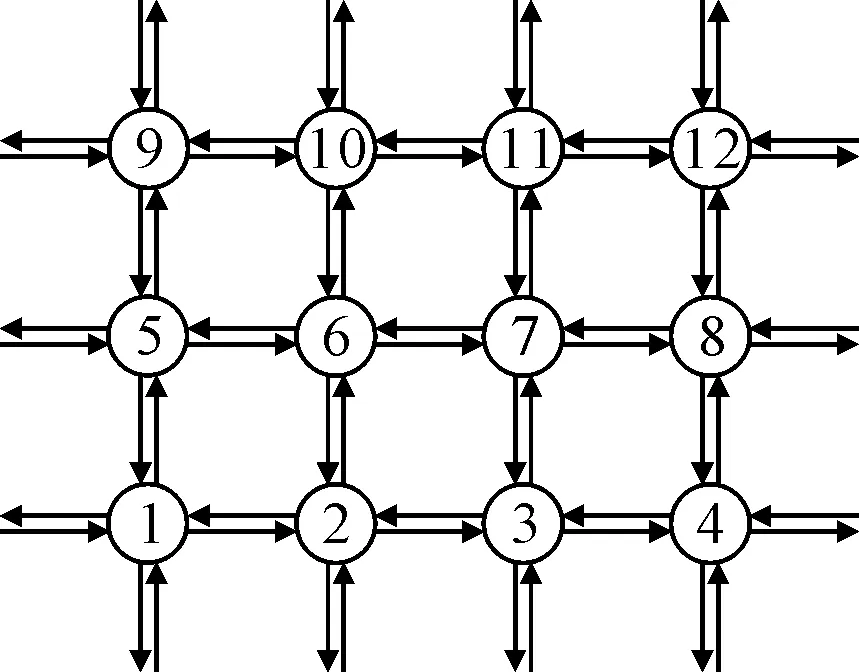
图1 试验路网

在区域路网中，交叉口6、8的信号配时参数为(C，g)=(80 s，37 s)，其余交叉口的信号配时参数为(C，g)=(90 s，42 s).仿真数据获取时间为10 800 s，通过流量不断增加，将仿真时间划分为6个时间段，并在交叉口入口道的上游30～40 m处设置检测器，每300 s完成一次交通参数数据的采集.

4.1 算法参数设置

在实验过程中，分别取Hadoop并行平台的2、4、6、8个节点进行实验.设置相同的串行算法和并行算法的参数：区域交通控制与诱导协同模型中涉及的参数有流量x1,…,x34、绿灯时长g1,…,g12、上行相位差ψ1,…,ψ12和下行相位差，其中，下行相位差可由周期和上行相位差做差得到.因此，算法的一条染色体包括58个变量，其长度为l=l1+l2+l3=12×34+6×12+7×12=564.种群规模：M=200；最大迭代代数：N=200；交叉概率Pc(i)和变异概率Pm(i)：通过自适应函数不断调整的自适应的概率.

4.2 实验结果与分析

运行VISSIM仿真软件，不断观测区域路网的交通流量变化情况.通过交通流量持续增加，路网中车辆的运行速度减慢，并出现排队长度.当VISSIM仿真进行到7 200 s时，区域路网中某些路段的排队长度比大于0.3，由此判断区域路网处于交通拥堵状态，实行区域交通控制与诱导协同.

1) 实施协同 通过VISSIM仿真软件采集7 200～7 500 s的路网交通参数数据，并将其作为串行遗传算法和并行遗传算法的输入，运行程序获得交通控制与诱导的参数值，见表1～2.由表1～2可知：两种算法在求解交通参数时得到的结果差异不大，但是在求解总行程时间时，明显看出并行算法的优势，因为并行算法弥补了遗传算法的缺陷，提高了最优解的质量.

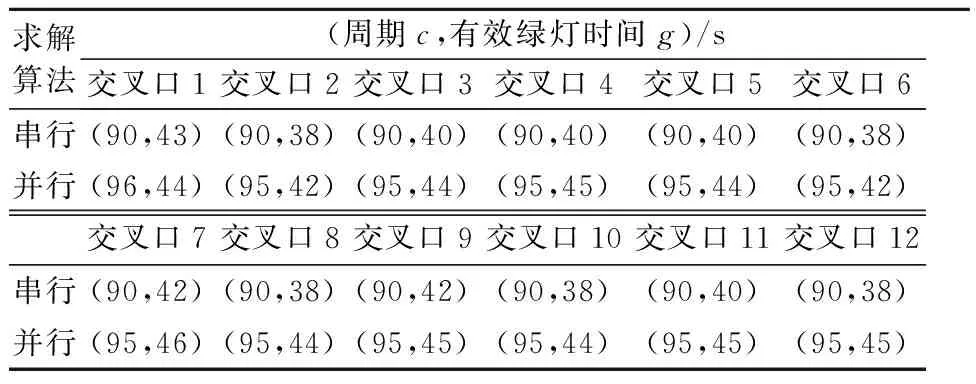
表1 信号配时参数求解结果

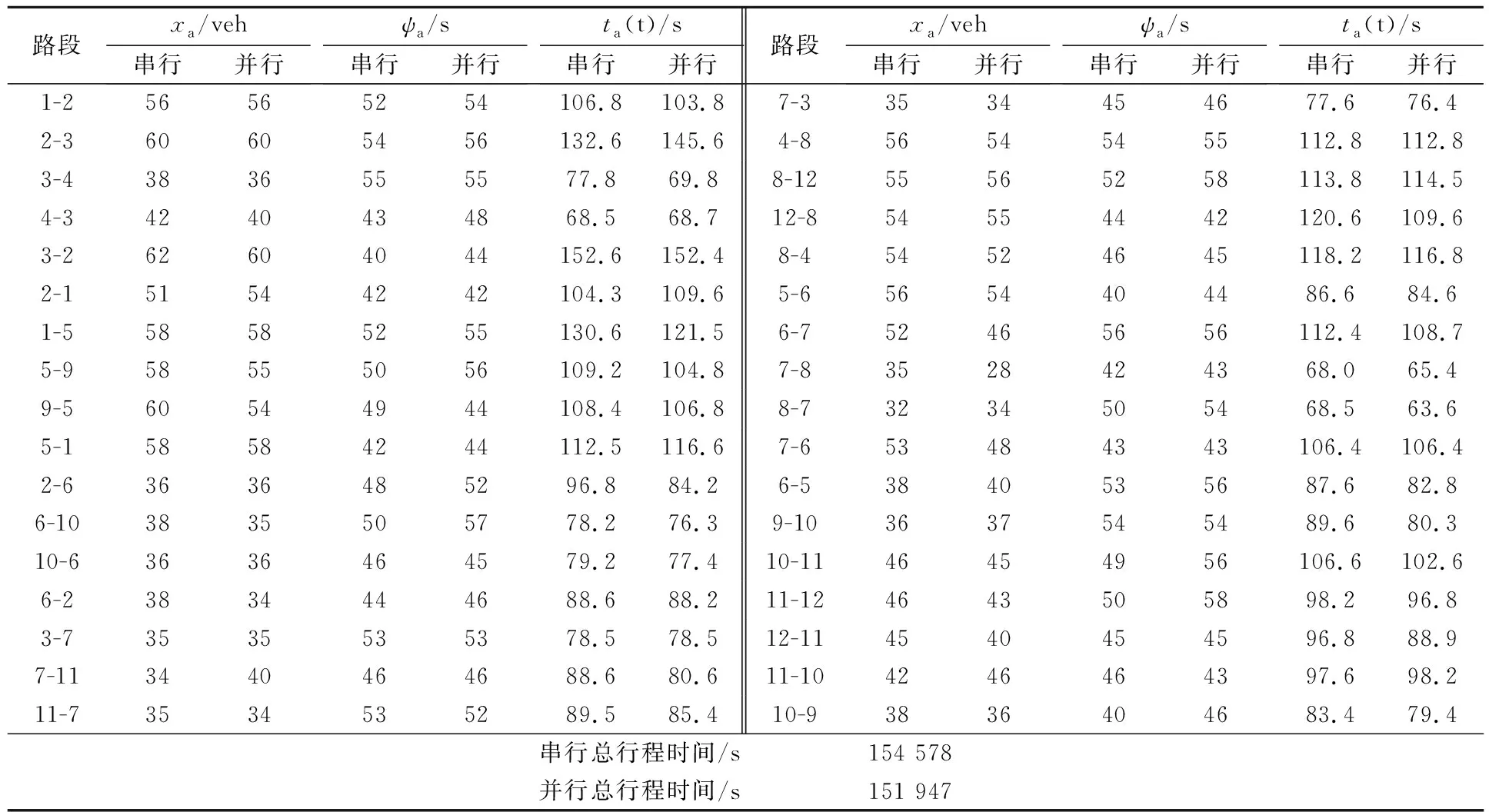
表2 路段参数求解结果

图2为实施交通控制与诱导协同后的区域路网各路段的流量对比图和行程时间对比图.由图2a)可知，通过实施协同，协同前比较拥挤的路段上的流量被分配到其他的路段上，从而避免该路段上的拥挤蔓延，说明实施协同有效地均衡了整个区域路网的流量.由图2b)可知，通过实施协同，减少了区域路网中各路段的行程时间，从而减少了整个路网的总行程时间，说明所提出模型具有有效性.

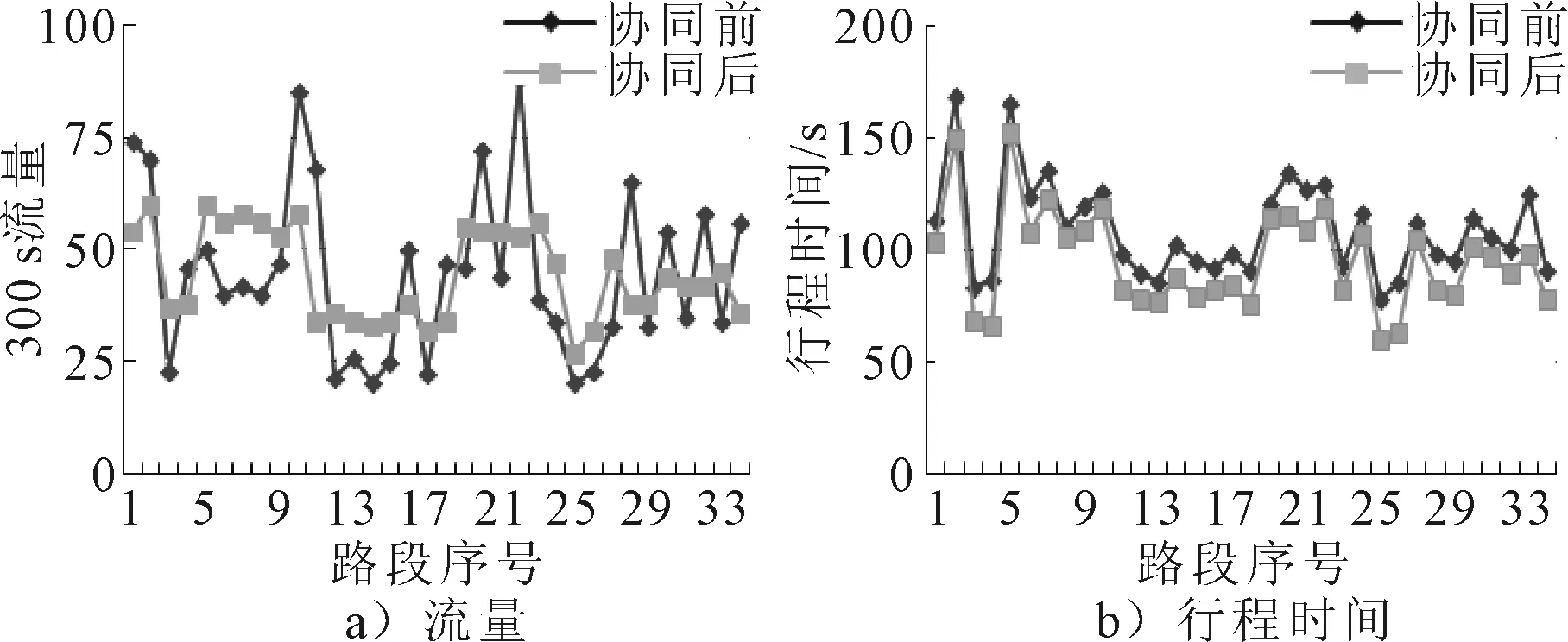
图2 协同前后流量和行程时间对比图

图3～4为基于MapReduce的遗传算法求解模型的运行时间对比图和加速比曲线图，其中并行节点数=1时是串行算法.由图3可知，当并行节点数=2时，运行时间减少的并不多，因为并行算法的Map阶段用时比较长，并行节点数过少，并不能明显提高算法的运行速度.然而，当并行节点数=4和并行节点数=6时，明显看出运行时间减小的幅度不断增大，说明并行算法优势表现出来了.但是，当并行节点数=8时，运行时间减少的幅度又变小了，主要因为并行节点数的增加会导致节点之间的通信负荷增大，可见并行节点数的选取要因情况而定，通过不断实验和反复对比，选择合适的并行节点数，从而提高并行算法的效率.由图4可知，通过不断增加并行节点数，并行算法的加速比不断提高，证明所提出的并行遗传算法具有良好的扩展性.当并行节点数=8时，取得最大加速比：S8=238.35 s/39.26 s=6.12，即当并行节点数=8时，并行算法比串行算法快6倍多，最小运行时间38.64 s，满足区域路网交通控制与诱导的需求.

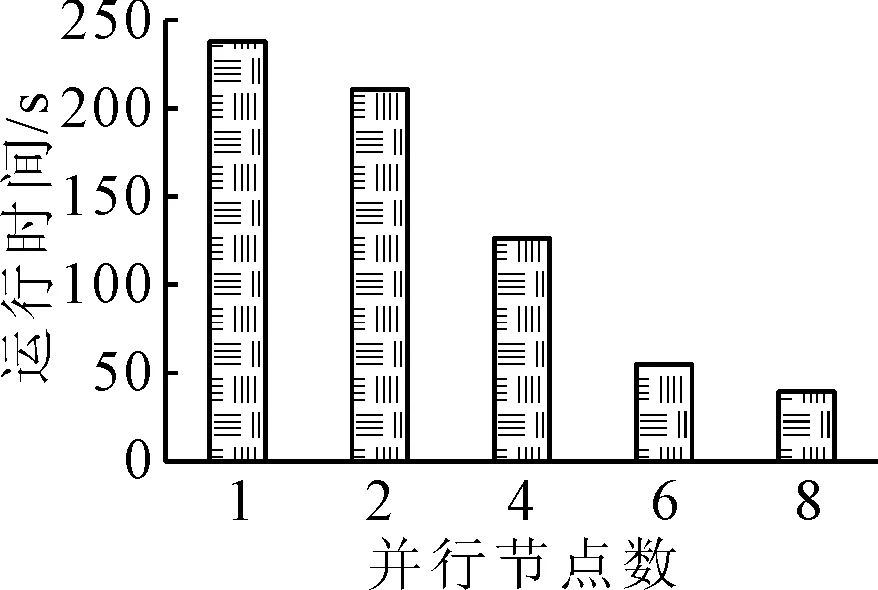
图3 运行时间对比图

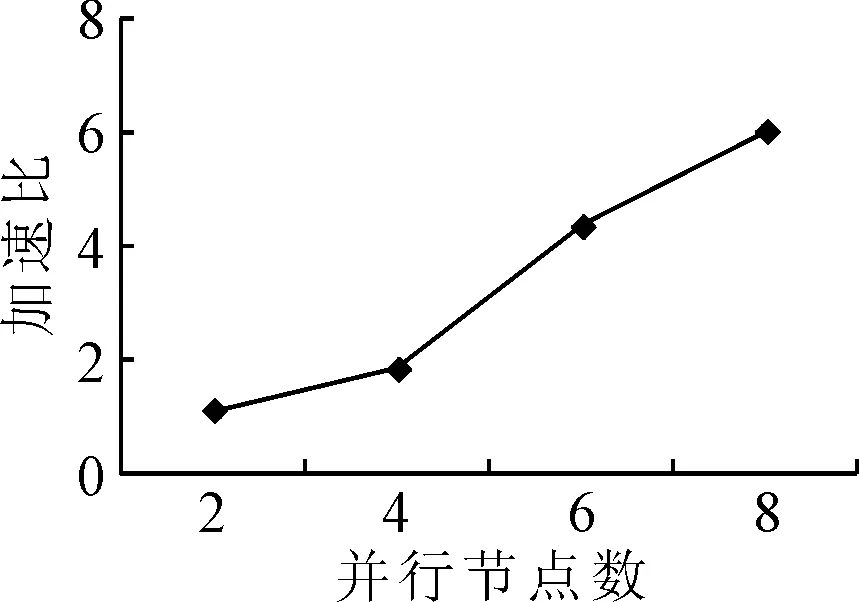
图4 加速比曲线图

5 结 束 语

以区域路网总行程时间最小为目标，构建了交通控制与诱导协同模型.①在计算行程时间时，通过引入排队长度参数，对行程时间进行了更有效的表达，使计算得到的行程时间更加准确；②在建立模型约束条件时，通过引入排队长度参数，更好地对相位差和有效绿灯时长进行了约束，使模型求得的参数更加准确.为了进一步提高协同模型的求解速度，文中采用基于MapReduce的并行遗传算法求解协同模型，通过实验发现，所提出的并行遗传算法在求解协同模型时的运行速度和所求得解的质量均有所提高，从而验证了所提出的协同模型和并行求解算法的有效性和可行性.