基于滑模观测信息的电动舵机自适应终端滑模控制
李 浩,梁 婕,王 尚,梁海波,王 瑞
(北京航天自动控制研究所,北京,100854)
0 引 言
舵机是飞行器控制系统中的关键部件,其性能的优劣决定了飞行控制效果的好坏。根据动力源的不同,飞行控制系统可以采用液压舵机、气动舵机和电动舵机。电动舵机体积小、质量轻,结构简单,维护方便,在飞行控制系统中得到广泛应用[1]。由于飞行过程中飞行器参数会发生变化,电动舵机的负载会随飞行条件的变化而改变,因此其控制器必需能够适应参数变化和负载扰动的影响,才能取得良好的动、静态性能。
滑模控制对不确定参数、扰动具有很强的鲁棒性,是控制不确定系统的一种有效方法[2]。终端滑模控制通过引入终端吸引子来改变系统的收敛特性,可以实现状态的有限时间收敛[3,4]。文献[5]提出一种非奇异快速终端滑模面,解决了奇异性问题,但对具体应用对象其控制律不易实现。文献[6]提出一种不确定二阶系统的快速终端滑模控制方法,可实现系统状态的有限时间收敛。上述控制方法中采用高增益来抑制系统不确定性的影响,保守性较强。文献[7]将自适应控制与鲁棒控制相结合,对参数进行在线估计,降低了控制保守性,但只能保证误差渐近收敛。文献[8]采用复合自适应律进行参数估计,按照估计值设计复合自适应非奇异终端滑模控制(Adaptive Nonsingular Fast Terminal Sliding Mode Control,ANFTSMC),可实现输出误差有限时间收敛,但在构造自适应律时需要使用系统状态的导数信息。
本文在舵机控制中设计自适应终端滑模控制器,利用滑模观测信息来构造自适应律,具有与一般复合自适应律相似的参数估计特性,但在设计自适应律时不需要系统状态的导数,可实现系统稳定控制与误差有限时间收敛。
1 问题描述
电动舵机作为一种位置伺服机构,主要由控制器、直流电机、减速器和位置传感器构成。一般直流电机电感较小,可忽略电感对系统动态特性的影响,舵机的数学模型为[1]

式中δ为舵偏角;u为电机电枢电压;J为转动惯量;KM为电压-力矩转换系数;B为阻尼系数;Af为摩擦力矩;hf为可选参数,一般hf选为较大的正数;ML为负载力矩;Δ为系统未建模动态。
令x=[x1,x2]T=[δ,δ˙]T,则可得系统状态表达式为

式中x=[x1,x2]T为系统状态向量;y为系统输出;b为控制增益,;a=[B/J,Af/J,ML/J]T;φ(x)=[-x2,-tanh(hfx2),-1]T。
a和b不确定,但满足以下假设:
假设1:系统参数和干扰有界,即:
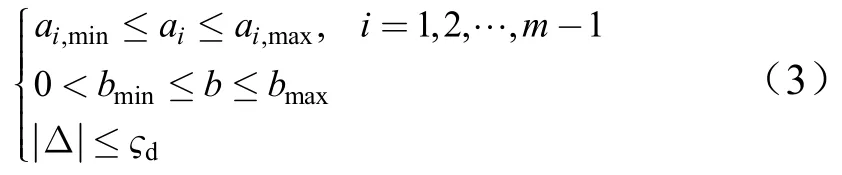
式中ai,min,ai,max,bmin,bmax和ςd已知。
假设2:系统参考轨迹xd连续,且其一阶导数和二阶导数有界并可得。
控制的目标是式(2),在满足假设1和假设2时,设计控制器,使系统输出误差e1=y-xd收敛为0,并且保证系统中所有信号有界。
2 控制器设计
对于式(2),设计如下非奇异快速终端滑模面[5]:

对σ2求导,可得[5]:
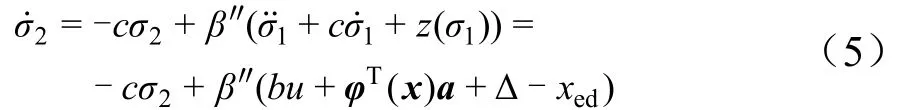
设计如下控制律:

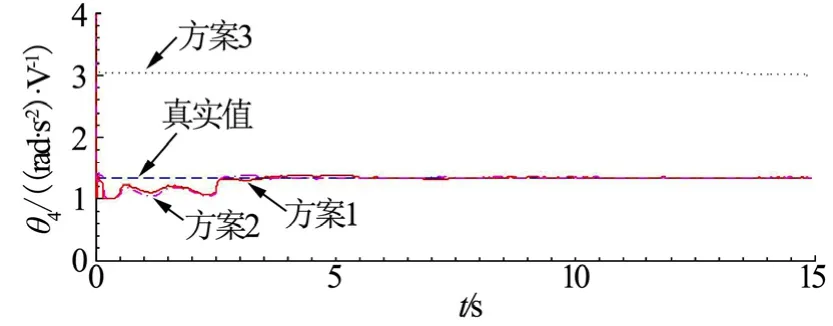
式中ua为自适应项;us为鲁棒项;k1>0;k2>0;,0 将式(6)代入式(5),可得: 对式(2),定义回归表达式如下: 由式(5)、式(8)可得: 设计自适应律为 若忽略Δ,则有: 因此,式(10)的自适应律中包含参数估计误差信息,与一般复合自适应律类似,但未使用系统状态的导数。式(10)中若不使用veq,而使用文献[8]中定义的预测误差ef,则可获得一般复合自适应律。 定理1:对于对象(2),采用式(6)和式(10)组成的控制器时,有: a)闭环系统稳定; b)若满足持续激励条件:式中α>0,I为m×m的单位矩阵,则系统状态有限时间收敛。 证明之前,先给出如下引理: 引理1[11]:,Γ为正定对角阵,有: 引理2[12,13]:假设m1>0,m2>0,0 引理3[12]:若连续正函数V(t)在时,≥0,其中α1>0,α2>0,0<μ<1,则,∀t≥t1,有V(t)=0。 证明: a)选取系统Lyapnov函数为V=V1+V2,V1=,,则, 根据引理1可知: 则: 则, 定义vd为 则vd≥0,并且有,由式(14)可知: 由式(20)和式(22)可知,当σ2≠0时,,满足Lyapnov稳定性条件。 b)当Ψ(x,u)满足式(15)的持续激励条件时,有: 其中, 下面分3种情况证明。 1)σ2≠0且。 当σ2≠0且时,由式(18)、式(19)知: 式(25)中,有: 以及: 由于0 由式(26)、式(27)可得: 根据定理3可知,V有限时间收敛,即,当t≥t1时,V(t)=0。而当V=0时,V1=0,则σ2=0。因此,当σ2≠0且+cσ1≠0时系统状态在有限时间内到达滑模面。 2)σ2≠0且+cσ1=0。 当σ2≠0且σ˙1+cσ1=0时,由式(4)知σ2=σ1,。令,将式(6)代入式(8),有: 当σ2>0时,由于,因此有-k3′sign(σ2)+Δ=-k3′+Δ<0,则, 由于0 3)σ2=0。 当σ2=0时,系统状态在滑模面上。再由定理2知,当系统状态到达滑模面之后,系统状态有限时间收敛至平衡点。 从上述3种情况的分析可知,系统状态在有限时间内到达滑模面,而系统状态到达滑模面之后,系统状态在有限时间内收敛到平衡点。 按照第2节中的步骤设计基于滑模观测信息的ANFTSMC。作为比较,还设计了一般复合自适应律的ANFTSMC[8]和一般自适应律的ANFTSMC。各控制器参数如下: a)方案1:采用滑模观测信息的ANFTSMC。 控制律中:β=0.1,c=10,γ=r=13/15,k1=100,k2=100,k3=4,kv=20;自适应律中:Γ1=[1,1.5,1,1.5]T,Γ2=Γ3=[1,2.5,2,2]T。为了降低抖振,采用tanh(h·)代替sign(·),h在控制器中为900,而在观测器中为50。 b)方案2:采用一般复合自适应律的ANFTSMC。 控制律中参数与方案1一致,自适应律中:Γ1=[2,1,2.5,1]T,Γ2=Γ3=[1,1,1.5,1]T,τ1=0.01。 c)方案3:采用一般自适应律的ANFTSMC。 在方案2中,令Γ2=Γ3=[0,0,0,0]T则可得采用一般自适应律的ANFTSMC,但需从新选择Γ1,这里Γ1=[50,600,750,2800]T。除Γ1、Γ2和Γ3,其余参数与方案2中相同。 图1至图4为系统参数的估计值,采用常规自适应律的ANFTSMC,虽然能够保证参数估计值保持在已知范围内,但很难逼近真值,而采用滑模观测信息的ANFTSMC和采用复合自适应律的ANFTSMC,参数估计值则能较快地收敛到真值。从图中可以看出,方案1和方案2在参数估计方面具有相似的性能。 图1 参数θ1的估计值Fig.1 Estimation ofθ1 图2 参数θ2的估计值Fig.2 Estimation ofθ2 图3 参数θ3的估计值Fig.3 Estimation ofθ3 图4 参数θ4的估计值Fig.4 Estimation ofθ4 图5为系统跟踪误差,方案1和方案2中参数能够较快地收敛到真值,系统误差收敛速度加快,系统稳态误差也大大减小,既可以提高参数估计的精度,又可以加快系统的响应速度。 图5 系统跟踪误差Fig.5 System Tracking Error 本文通过构造滑模观测器,使观测状态到达观测器的滑模面,通过低通滤波器提取出观测器的等效输入信号,该等效信号包含系统参数估计的误差信息,然后将该等效信号应用于自适应律中,该自适应律具有与一般复合自适应律相似的参数估计特性,但不需要系统状态的导数。采用该自适应律,设计了电动舵机的自适应终端滑模控制器,实现了系统稳定控制与误差有限时间收敛。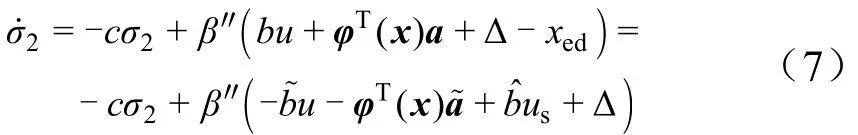

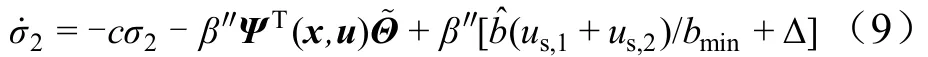





3 稳定性分析

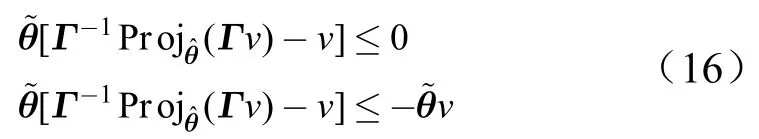




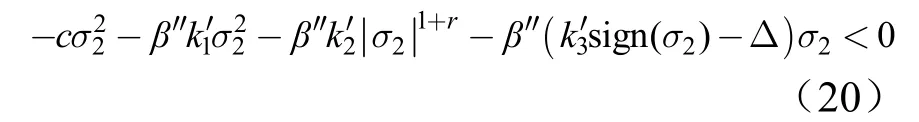
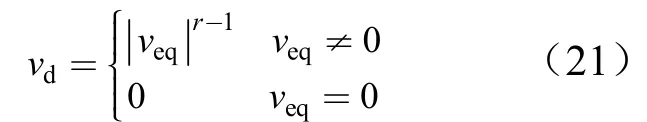


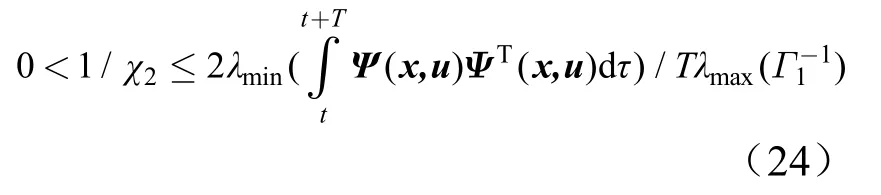

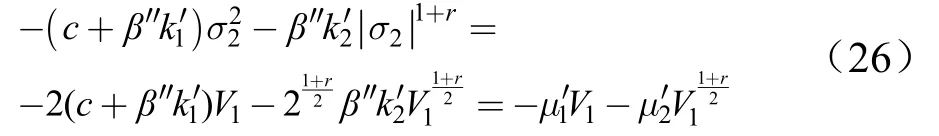

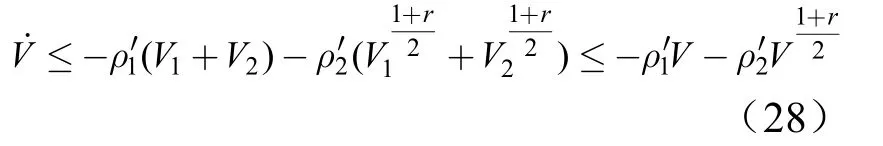



4 仿真与分析




5 结束语

