以高精度惯组为参考的MEMS惯组参数在线估计方法

赵欣艺，高晓颖，李宇明，裴圣旺，李 瑜

（1. 北京航天自动控制研究所，北京，100854；2. 中国运载火箭技术研究院，北京，100076； 3. 北京东方计量测试研究所，北京，100086）

0 Introduction

In the launch vehicle mission, the navigation system needs to provide reliable and accurate navigation information. At the same time, the advantages of low cost, light weight and low power consumption are also very important.

Redundancy design is one of the ways to improve the reliability of navigation system of the launch vehicles. At present, the domestic launch vehicles CZ-3A series and CZ-2C series adopt two sets of redundant laser inertial units, and the CZ-5 and CZ-7 launch vehicles adopt two sets of laser inertial units and one set of optical fiber inertial units[1]. The European Arian rocket was designed with double inertial units. SpaceX Falcon rocket was designed with distributed redundant inertial units[2]. Although the redundant design improves the reliability of the navigation system, it causes the problems of high cost, large volume, high power consumption and so on.

As a kind of micro inertial unit, MEMS is not as accurate as optical inertial unit. But with great advantages in volume, weight and cost, it can be considered as a part of redundant inertial unit design. Moreover, the stability of single powering of MEMS IMU devices has certain advantages[3]. In this new redundancy mode, theparameters of MEMS IMU can be estimated online by using the information of high-precision IMU, which avoids the tedious calibration before launch and makes use of the stability of single power on to a certain extent.

According to the measurement model of inertial devices, the error sources of inertial devices mainly include zero order error, installation error and random error. The error of inertial devices leads to the inaccuracy of the output measurement value of inertial navigation system, which is an important factor leading to the accumulation of inertial navigation error. In the parameter estimation of inertial devices, the relevant parameters in the measurement model of inertial devices are estimated to compensate the output of inertial devices, so as to obtain more accurate inertial navigation information. In inertial parameter estimation, the IMU components are usually calibrated in the laboratory before launching.

The foreign on-line calibration technology for inertial devices first started with Mohinder[4]. The parameter estimation of inertial devices is realized through multidimensional filter by the principle of Kalman filter. At the beginning of the 21st century, Shin E H of Canada proposed a field calibration method[5]. Later, Syed and others took MEMS inertial navigation device as the research object, and adopted the multi-position calibration method to realize the calibration of MEMS inertial navigation device parameters, and the calibration accuracy was demonstrated[6]. In 2010, Nieminen and others improved the multi-position calibration algorithm for inertial measurement unit, and achieved good results[7]. In 2016, Qin put forward an online calibration method, of which the velocity-position measurement error is the observation[8]. In 2017, Dranitsyna proposed a calibration method of inertial devices based on the solution of strapdown inertial navigation[9]. The selection method of maneuver is also given.

There are also many domestic scholars who study on-line parameter estimation of inertial navigation system. Lu and Wang’s research[10]aiming at the problem of on-line calibration of airborne strapdown inertial navigation system, constant error parameters and calibration coefficient parameters are estimated by designing maneuver trajectory based on GNSS. According to the research[11], the information of star sensor is added to the navigation system. The simulation results show that the method can accurately estimate the parameter of the sensors.

In this paper, an on-line parameter estimation method of low precision IMU based on high precision IMU is proposed. Considering the variation of IMU parameters with the environment, taking the linearity as the index, the sliding window mode is used to select the historical data length to realize the on-line parameter estimation of low-precision IMU.

1 Bulid the Measurement Model.

The measurement models of high precision laser IMU and low precision MEMS IMU are shown in equation (1) and equation (2).

In matrix form:

In the process of parameter estimation, it is impossible to determine the output values of the angular increment and apparent velocity increment of the three axes in the body-fitted coordinate, so the corresponding components in the body-fitted coordinate are calculated by the high-precision IMU measurement results.

WhereDh1′is the mounting matrix of high precision gyro by calibration,Dh0′is the zero order term of high precision gyro by calibration,，andare the angular increment in body-fitted coordinate calculated by high precision gyro.

The model of accelerometer is similar to that of gyro, so it is outside the scope of this article.

2 Least Square Method for State Parameter Estimation

2.1 Least Square Method

The least square method was first proposed by Gauss, a German mathematician, and is widely used in the fields of science and engineering technology. In the traditional discrete calibration of inertial device laboratory, Through the output of turntables and inertial devices at different positions, multiple sets of data can be obtained, and high-precision parameter calibration results can be obtained through the least square method by the high-precision turntable and accurate earth gravity acceleration.

In the redundant combination mode proposed in this paper, the output of high precision IMU can be used as the theoretical output of low precision IMU calibration. The output of high precision IMU is used as the benchmark to calibrate the low precision IMU, so that the measurement result of low precision IMU is close to the high precision IMU as much as possible.

Record the high and low precision IMU output ofntime points, and plug them into the gyro measurement model. For the output ofx-position MEMS gyro, the equation can be established:

The least square method was used to estimate the parameters. The measurement equation of the system is as follows:

The least square estimation formula is as follows:

2.2 The Linearity of Measurement MatrixH

It can be seen from the form of least square algorithm that the main influence of parameter estimation accuracy comes from the form of measurement matrix H. When the linearity of each row of data of H-matrix is high, the dispersion of data in measurement matrix is low, that is, the input data are similar, which is unfavorable for parameter estimation.

The linearity ofH-matrix is evaluated for the selected window , which is the basis of window length selection.

For the measurement matrix, each line element corresponds to the apparent velocity increment and angle increment calculated by high precision IMU in the body-fitted coordinate at a certain time, which contains error. If the linear correlation is low, it is shown that the data is diversified and is more favorable for parameter estimation. We consider that the data in the measurement matrix contains the noise effect of the high-precision IMU. By setting the threshold, comparing each row of vectors in pairs and combining the two rows of vectors with higher linearity, the linearity index of data in a certain time window can be obtained. This method is simple and reliable. However, in the case of long window length, pairwise comparison of each row of vectors will lead to large amount of calculation and slow down operation speed, which is not conducive to the real-time calculation of linearity index.

We observe the characteristics of the output data of the gyroscope and accelerometer in the body-fitted coordinate. For the general trajectory, the data fluctuation at the initial time of launch is obvious, the linearity is low, and there is almost no multiple relationship between vectors. When the carrier enters the stable flight state, its output swings in a very small range, and the output of the gyro and accelerometer in the stable flight phase has almost no multiple relationship. Therefore, the calculation method of the above linearity index is improved.

Firstly, the measurement matrix data is quantized to reduce the influence of noise on the measurement matrix. The measurement matrix is calculated by the high-precision IMU, and the data contains the noise of the high-precision IMU. Because the noise of high-precision IMU is small, in order to analyze the linearity of the measurement matrix data conveniently, the measurement matrix is amplified and rounded with the noise level as the reference, andH′ is obtained. In this case, count the number of unrepeated row elements inH′, and define the number as the linearity index corresponding to the measurement matrixH.

2.3 Adaptive Sliding Window Parameter Estimation Process

In the process of calculation, if the damage of high-precision IMU is not considered, the data of high-precision and low-precision IMU will be generated continuously with the launch time. The amount of data that can be processed accumulates over time. This section considers the increasing amount of data over time. If the change of parameters with time is not considered, the amount of historical data will accumulate with the increase of flight time, which is beneficial for parameter estimation. However, the parameters to be estimated may change during the flight. If all the historical data are still used in the parameter estimation at the current time, because the parameters at the current time have changed, the historical data at a distant time will have an impact on the parameter estimation at the current time. In this case, it is unreasonable to continue to use all the historical data to estimate the parameters at the current time.

We proposed the adaptive sliding window parameter estimation process to estimate the parameter. The flowchart is shown in figure 1.

Fig.1 Flowchart of Adaptive Sliding Window Parameter Estimation.

First, the length of data is judged according to the input historical data. If the length of historical data does not reach the minimum window length, the linearity index of all historical data is calculated. Then if the linearity index meets the threshold, the least square method is used to estimate the error parameters and output the estimation results, else if the linearity index does not meet the threshold, it will wait for the input of new data. If the length of the historical data has reached the minimum window length, the minimum window length data is selected from the nearest data to calculate the linearity index. If the linearity index reaches the threshold, the least square method is used to estimate the error parameters and output the estimation results. If the linearity index does not reach the threshold, increase the length of the data window, calculate the linearity index and judge the threshold again, and continue to cycle until the threshold requirements are met. If the final window length has been expanded to the set maximum windowlength and the requirements still cannot be meet, the last parameter estimation meeting the conditions is output.

3 Simulation

The experimental parameter setting: The bias error of laser gyro: 0.05 °/h; The bias error of quartz accelerometer: 0.0001 m/s²。The bias error of MESE gyro: 5 °/h; The bias error of MESE accelerometer: 0.01 m/s²。

The calculation results of the gyros are shown in figures 2 to 5. Figures 2 to 5 show the error coefficient estimation results and condition values of the gyroscope. Figure 2 and figure 3 show the parameter estimation error based on adaptive sliding window. Figure 4 shows the relationship between the calculated value of the index and the threshold value. Figure 5 shows the currently selected window length and the effectiveness of the estimation. Comparing with Figure 3 and Figure 5, it can be found that the zero order error and installation angle error of the gyro are obviously smaller when it is judged as effective estimation. The fluctuation of zero order error is small. The error of installation angle is below 0.05 degree in the period of effective estimation. The corresponding statistics are given in Table 1. The same method is used to estimate the parameter of accelerometers. The result is shown in Table 2.

In general, as shown in Table 2, this method is still effective for the error coefficient estimation of accelerometer. In the effective range of the estimation, the mean value of the zero order error is 1×10-4m/s2, and the mean value of the installation error is close to that of the gyro estimation, about 0.06°.

Fig.2 Result of Gyro Zero Order Term Parameter Error Estimation with Adaptive Sliding Window

Fig.3 Result of Gyro Erection Angle Error Estimation with Adaptive Sliding Window

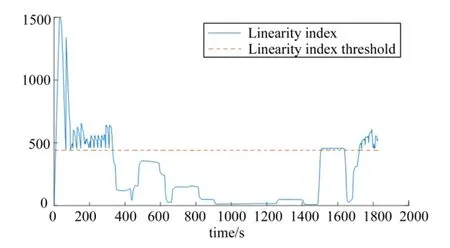
Fig.4 The Threshold and Change in Linear Index Over Time

Fig.5 Window Length of Gyro Parameter Error Estimation and the Flag of Decision

Tab.1 The Parameter Error of Gyros with the Effective Result

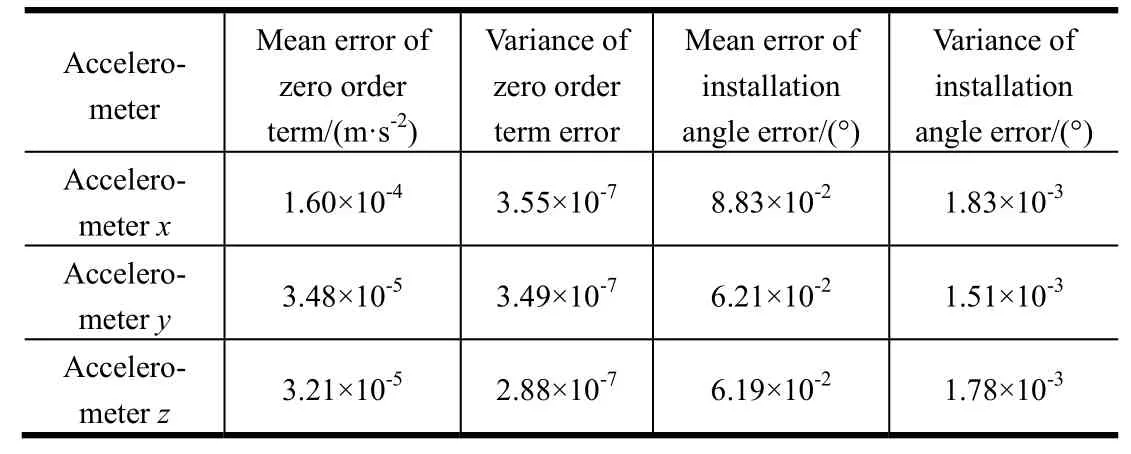
Tab.2 The Parameter Error of Accelerometers with the Effective Result

4 Conclusion

Aiming at the redundant structure of low precision MEMS IMU and high precision IMU, the information of high precision IMU is used to estimate the parameters of low precision IMU online. It solves the problem that the redundant mode will lead to a large amount of work in the pre launch calibration of multiple inertial devices. Considering the high stability of single power on of low precision MEMS inertial unit (IMU) and the problem that the parameters of IMU may change during flight, an adaptive sliding window estimation method is proposed, which uses linearity as an index to select an effective parameter estimation interval. The simulation results show that the method is effective.