火箭发动机流场快速计算方法研究

陈 浩，李晓轩，杨依峰，杨天鹏，张昱煜

（北京航天长征飞行器研究所，北京，100076）

0 引 言

基于化学能的小型火箭发动机是空间飞行器进行姿态控制的有效手段，基于CFD的计算方法能够实现推力的精确评估[1,2]。但是，对工业界来说，评估方法不仅需要足够精确，还需要足够快速才能实现迭代优化设计。

对基于CFD的评估方法而言，其中的气体模型和计算区域都是可以调整以在精度和计算效率之间进行折中的变量。基于真实组分的气体模型要比基于等效比热比的单组分气体模型更精确，但由于引入了额外的组分方程，计算效率更低。在计算区域方面，内外流一体化方法要比仅考虑内流的计算方法精度更高，但计算时间也随着计算网格的增加而增加。

本文采用CFD方法从气体参数和计算区域两个方面开展研究，比较了采用等效单组分气体和仅考虑内流这两种近似计算方法所引入的偏差以及这些简化措施带来的计算效率提升的程度。在此基础上，建议了一种计算效率较高并且计算精度可以接受的发动机数值模拟方法。

1 计算方法

本文通过有限体积法求解二维轴对称坐标系下的NS方程（含组分输运方程）[3]，但不考虑化学反应和湍流的影响。

式中Q=[ρρuρvρEργi]；F为无粘通量；G为粘性通量；AF为无粘轴对称交叉源项；AG为粘性轴对称交叉源项。值得注意的是，控制体Ω的定义为二维控制体的面积与其平均半径的积。

对该方程进行求解时，无粘通量通过TVD格式计算，限制器为minmod格式。采用LUSGS格式进行时间推进。在边界条件方面，物面均采用无滑移边界，在内外流一体化方法的远场处采用基于黎曼不变量的无反射条件[4]，在仅内流方法出口处采用速度出口边界。

2 算例介绍

本文采用的喷管内型面尺寸如图1所示。针对该喷管划分的计算网格如图2所示。为了保证计算精度，网格在物面附近、喉道附近进行了加密。图2中的网格将直接用于内外流一体化计算，在进行仅内流计算时仅保留喷管内部的网格。

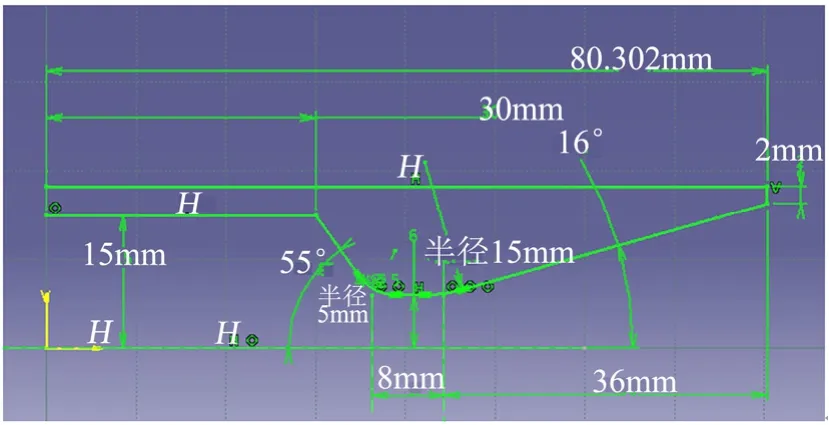
图1 喷管几何形状Fig.1 Nozzle Profile of the Rocket Engine

图2 计算网格Fig.2 Computational Grid

发动机燃气的各组分和属性如表1所示。该组分表将用于真实组分气体模型的计算。

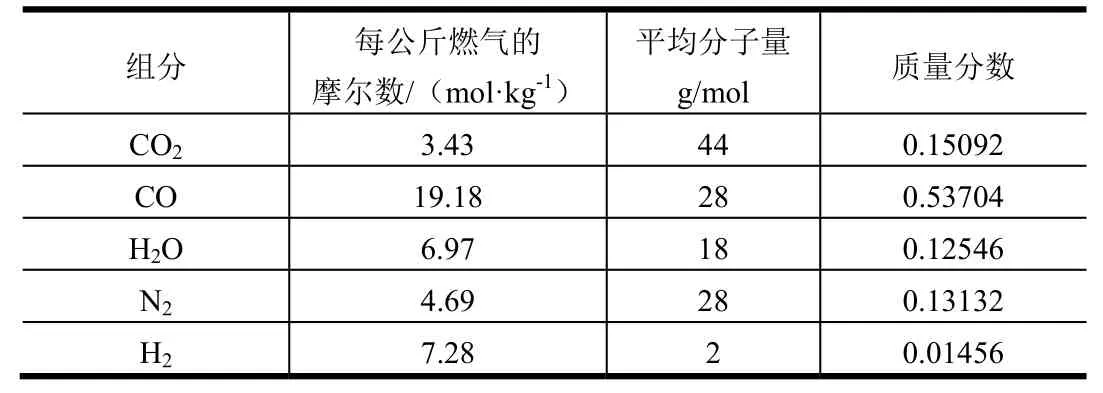
表1 气体组分Tab.1 Engine Gas Properties

由真实组分气体折算的等效单组分气体的属性如表2所示，折算方法见文献[5]。该气体属性将用于等效单组分气体模型的计算。

表2 等效单组分气体Tab.2 Equivalent One Component Gas Properties

发动机喷管的入流边界条件如表3所示。

表3 入流边界条件Tab.3 Inlet Boundary Conditions

在内外流一体化方法中的远场边界条件见表4。

表4 远场边界Tab.4 Far-field Boundary Conditions

根据本文的研究目的，最终确定的各算例如表5所示。通过3个案例的对比可以分别获得不同气体模型和不同计算区域对发动机喷流的计算精度和效率的影响。

表5 算例说明Tab.5 Cases Description

3 计算结果分析

3.1 真实气体与等效气体

不同气体模型条件下获得的发动机推力和各自的计算时间见表6。从表6中可知，采用简化的等效单组分气体模型后，发动机推力有0.95%的偏差，而计算效率提高了2.5倍。

表6 不同气体模型算例对比Tab.6 Comparison of Cases with Different Gas Models

不同气体模型条件下获得的马赫数分布和压强分布分别如图3和图4所示。由图3和图4可知，采用简化的等效单组分气体模型后，出口处的马赫数分布略有差异而压强分布基本一致。

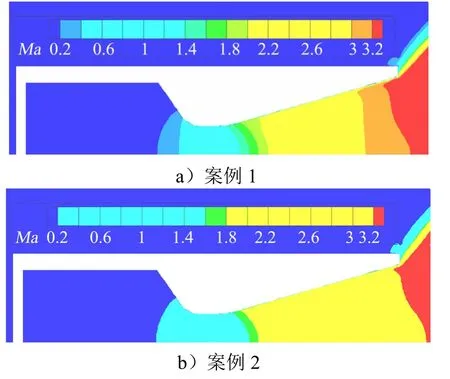
图3 不同气体模型马赫数分布对比Fig.3 Mach Number Distribution of Different Gas Models

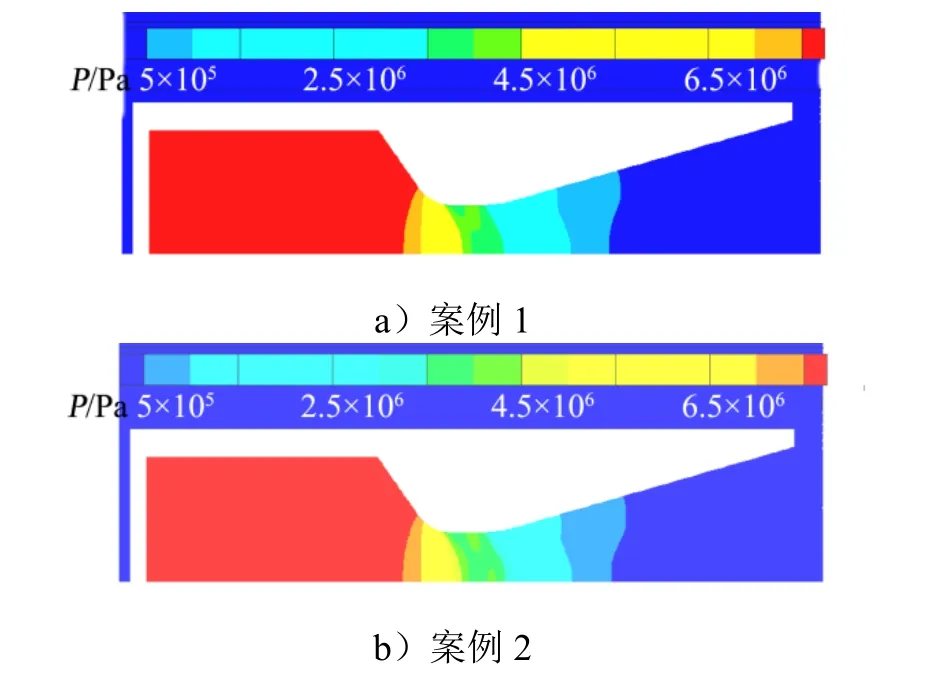
图4 压强分布对比Fig.4 Pressure Distribution of Different Gas Models

3.2 内外一体化网格与仅内部网格

不同计算区域条件下获得的发动机推力和各自的计算时间见表7。从表7中可知，采用仅内流的简化计算方法后，发动机推力有0.06%的偏差，而计算效率提高了14.2倍。

表7 不同计算区域算例对比Tab.7 Comparison of Cases with Different Inlet Boundaries

不同计算区域条件下获得的马赫数分布和压强分布分别如图5和图6所示。由图5和图6可知，不同计算区域条件下，出口处的马赫数分布略有差异而喷管内的压强分布基本一致。

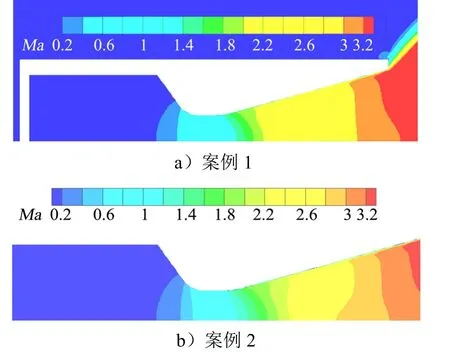
图5 不同计算区域马赫数分布对比Fig.5 Mach Number Distribution of Different Inlet Boundary Conditions

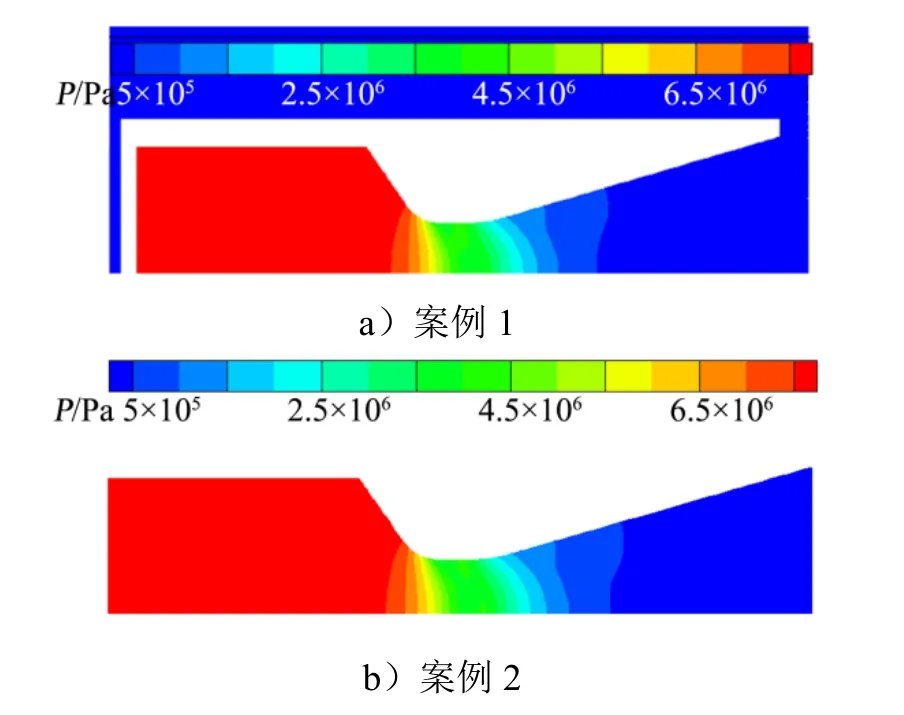
图6 压强分布对比Fig.6 Pressure Distribution of Different Inlet Boundary Conditions

4 结 论

通过研究可得出以下结论：

a）采用单组分的等效气体仅会造成0.95%的推力偏差，而计算效率能够提高2.5倍，因此采用等效单组分气体可以在基本不影响计算精度的前提下提高计算效率。

b）采用仅内流的简化计算方法对推力计算几乎没有影响，而计算效率能够提高14.2倍，因此仅内流的计算方法可以在不影响计算精度的前提下显著提高计算效率。

c）从计算精度和计算效率两个方面进行综合考虑，建议在工程设计中直接采用仅内流的简化计算方法进行火箭发动机的推力评估。