肼类单组元发动机冷起动过程温度敏感性研究
冀 鹏,雷凡培,梁树强,肖明杰
(1. 西安航天动力研究所液体火箭发动机重点实验室,西安,710100;2. 中国船舶集团有限公司,北京,100044; 3. 航天推进技术研究院,西安,710100)
0 引 言
肼类单组元发动机是运载火箭和各类航天器姿态控制、轨道控制使用最广泛的推进系统,其性能以及稳定性直接影响着运载火箭和航天器的控制精度和可靠性[1,2]。近年来随着航天器飞行任务的增多,对单组元发动机的环境适应性愈加严苛,单组元肼发动机在冷起动时,时常出现起动响应延迟长、起动压力峰大的现象。一方面较长的起动响应延迟难以满足总体对推进系统的响应要求,另一方面较高的起动压力峰也降低了发动机的结构可靠性,可能导致发动机结构破坏。亟待对肼类单组元催化分解发动机冷起动工作过程开展深入的研究工作。
采用催化分解产生热燃气的肼类单组元发动机,推进剂进入推力室后涉及在催化床这种多孔介质中的多相多尺度流动、均相热分解和异相催化分解等复杂的物理化学过程,目前对该过程的研究主要依靠试验。Hearn[3]在研究脉冲工作对催化床寿命影响时发现,在脉冲工作模式下冷起动压力峰不会发生在较短的脉冲过程中。Kagawa等[4,5]采用可视化技术研究催化床内液态肼流动状态,发现相较于温启动和热启动,冷起动时液态肼的渗透面积更大、渗透距离更远。此外,火星着陆飞船[6]、阿里安5号运载火箭[7]、NASA空间飞行器[8,9]等所采用单组元发动机研制过程中,也主要采用试验手段来考核和鉴定发动机的冷起动能力并评判其对发动机性能的影响,发现过低的起动边界温度会导致肼推力器的使用寿命大大降低。单组元发动机的冷起动仿真研究方面目前尚未有公开文献发表。
一般认为温度较低时化学反应速率会减慢,但在单组元肼类发动机冷起动过程中,会出现数倍于温启动或热启动的响应延迟,并且延迟过程中室压维持不变,然后突然产生明显的压力峰,该现象与低温导致化学反应变慢机理并不契合。因此考虑该现象与微观催化分解过程有关。肼分解用催化剂并不是简单的球形或柱形颗粒结构,而是由复杂的浸渍、焙烧等制备工艺得到的具有众多微孔通道的层状骨架结构[10]。Sanglovanni等[11]通过试验观察到在低温情况下,液态肼滴定到催化剂颗粒后迅速浸湿了疏松的催化剂颗粒,在试验后发现催化剂颗粒发生了明显的破碎。赵许群[12]在对低温下催化剂的失活机理进行分析时提到,在低温下肼会在催化剂微孔内短时剧烈分解产生较大内应力导致催化剂颗粒破碎。
综上,现在仍然缺乏对肼类单组元发动机冷起动过程的完整过程认识和可靠的数值仿真方法,导致在发动机研制过程中主要依赖试验来预判和评价发动机的低温起动特性。因此结合催化剂微孔通道内流动-反应和经典燃烧时滞理论,开展肼类单组元发动机冷起动过程数值仿真分析,研究初始温度对冷起动压力与延迟时间的影响,揭示发动机冷起动延迟长、压力峰高的主导因素。
1 发动机典型组件的动力学模型
对于恒压挤压式的单组元姿控发动机,工作过程中贮箱压力基本保持不变,因此假设贮箱内气体压力恒定,主要建立起液路推进剂供应系统以及催化床的动力学模型。
1.1 管路模型
在建立液体管路模型时不考虑管路的变形,认为管道为刚性的;管路内液体是一维的,管道横截面上的速度分布是均匀的。本文主要关注的发动机起动过程属于低频动力学问题,因此采用分段集中参数的管路模型即可满足精度要求。根据经验,一种比较保守的方法是将分段管长取波长的4%以内,即管路分段长度应满足:Lmax≤0.04a/fmax。此外,毛细管、阀门流道等在一定程度上也可以等效为液体管路。
对于特定的一段长度、直径、截面积和体积分别为L、d、A、V的管路,考虑惯性、粘性时管路瞬变流:
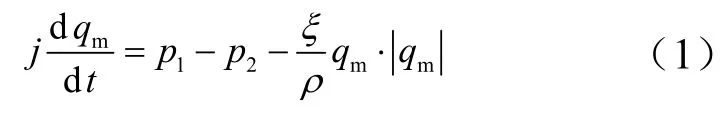
式中qm,p1,p2分别为管路流量,管路入口和出口处压力;j为管内液体的惯性系数,ALj/=;ξ为总流阻系数,由管路沿程损失和局部损失组成,取决于流体管路的形状和尺寸、管壁粗糙度及流体在管路的流动状态等,其中流体流动状态常采用雷诺数来表征。
考虑液体压缩性的方程:

式中z为管路的流容系数,z=V/a2,表征管路流体的压缩性。
1.2 催化床模型
本文采用反映平均效应的零维模型。在建立催化床模型时作如下假设:分解产物为理想气体;不考虑气体的不均匀性和波动过程;不考虑催化床内催化剂活性点处失活的影响。
1.2.1 冷起动延迟模型
在单组元发动机冷起动时,考虑到此时催化床和推进剂的温度都比较低,液体推进剂喷入催化床内后难以快速蒸发而以液态形式流入催化剂颗粒的间隙中,同时催化剂上微孔直径较小(直径范围从10A到104A),在毛细作用下渗透到催化剂颗粒微孔的内部。进入微孔后推进剂缓慢蒸发,在催化剂微孔内部形成气液分界面,部分气相推进剂通过质量扩散到微孔壁面的活性位置分解得到氨气、氢气和氮气等。这些分解气体被催化剂外的液体推进剂堵塞在微孔内,随着分解产物逐步增多微孔内部压力逐渐升高,推进剂分界面逐步向微孔外部移动,微孔内部压力最终会大于毛细压力而使得分界面被挤压到颗粒外部。大量的分解产物从微孔中溢出,气相推进剂得以实现催化剂间隙到微孔活性位置的快速扩散分解,在这两者共同的作用下催化床内产生了较大的压力峰。将冷起动延迟时间定义为从液体推进剂喷入催化床内到气体产物溢出催化剂微孔这段时间。
基于上述冷起动过程催化床内部复杂过程的分析,下面将对催化剂颗粒内部进行建模分析,计算气液分界面在颗粒微孔内部压力的作用下逐渐推移到微孔外过程,得到单组元发动机冷起动延迟时间。
首先以催化剂颗粒内部气体为研究对象,分析催化剂颗粒微孔内部压升过程。根据微孔毛细理论[13],微孔内部气相产物沿颗粒径向的平均速度通过泊肃叶方程描述如下:

式中vm为微孔内部气相的平均速度;R为大孔的特征半径;μg为气相产物的粘性系数;δ为催化剂微孔弯曲因子;P为微孔内压力;r为流体径向半径。
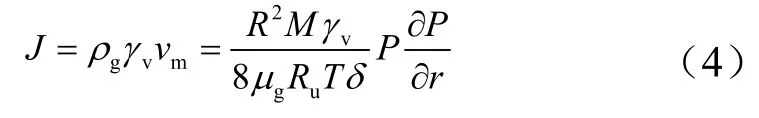
式中J为气相产物径向单位面积上的质量流量;γν为空隙分数,指单位体积颗粒内气相填充的比例;M为气体产物的平均摩尔质量;Ru为气体常数;T为气体温度,假设在较短的冷起动延迟时间内气相产物的温度与初始温度相差不大。
在微孔内考虑气体的连续方程:
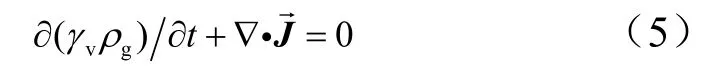
联立式(4)和式(5)可得催化剂颗粒内部压力:

在边界条件方面,初始时刻微孔内压力为环境压力;而在颗粒中心的压力梯度为零,还有一个边界条件是在微孔内部移动的气液分界面气相质量守恒,即微孔内部气相产物的质量变化等于在分界面上蒸发和颗粒内部扩散气态肼的质量变化。则初边值条件如下:
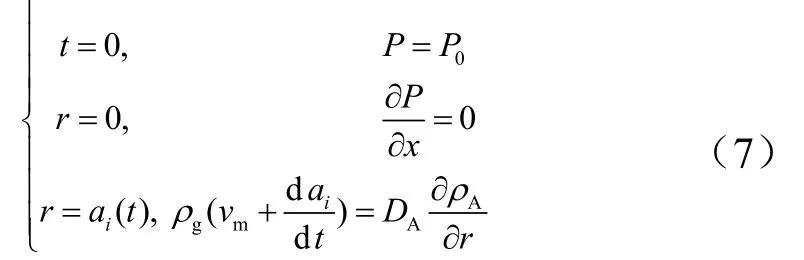
式中DA为气相推进剂在其分解产物中的扩散系数,。
为了求解内部压力方程,还需要知道分界面随时间的变化ai(t),以及在分界面上气相肼的摩尔质量沿微孔径向分布。颗粒内部气液分界面的径向位置可用描述液体在长管中流动规律的泊肃叶方程得到:
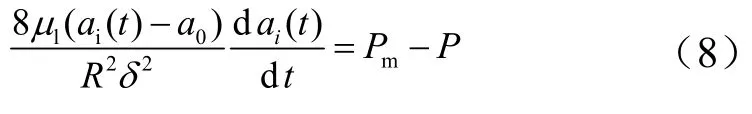
式中μl为液态推进剂粘性系数;Pm为毛细压力,;σ为液态推进剂表面张力,随温度变化;θ为接触角。
根据在分界面后局部气态肼考虑分解反应的质量守恒方程得到:
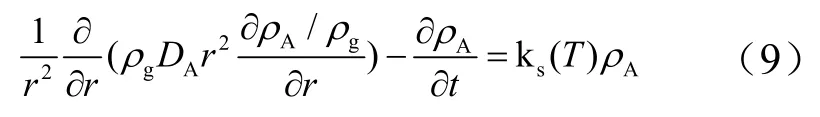
式中y为液体推进剂渗入催化剂颗微孔内的长度;为液体推进剂的密度;ks(T)为推进剂的异相反应速率常数,ks=1010exp(-1389/T)。
这样得到了完整的控制方程与初边值条件,经过无量纲化和小扰动法计算得到分界面位置ai(tlign)=0时,即气体分解产物从微孔中溢出,此时得到了冷起动延迟时间tlign为[14]
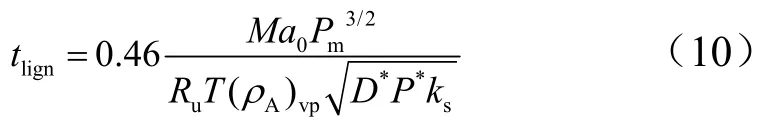
式中 (ρA)vp为推进剂的饱和蒸汽密度,与温度相关[1]。
1.2.2 催化床建压过程模型
考虑到催化床内复杂的物理化学过程,引入燃烧室时滞模型[15],假设在该转化时间内推进剂的转化速率均匀,且分解后的气体在任何瞬时分布均匀,即氨的解离过程也近似认为与DT-3的分解过程同时进行。 则液体推进剂及气体分解产物在催化床中的质量变化分别为
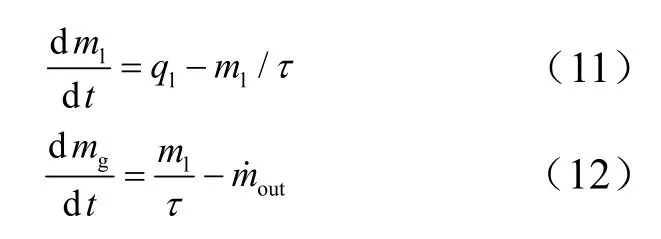
式中mout是催化床出口的气体质量流量,;At为喷管的喉部截面积;ml、mg分别为催化床内积存的液体推进剂质量和气体质量;ql、分别为流入催化床内的液体推进剂质量流量和流出推力室的气体质量流量;τ为推进剂的转化时间,可根据推进剂的分解延迟期试验[16]得到。
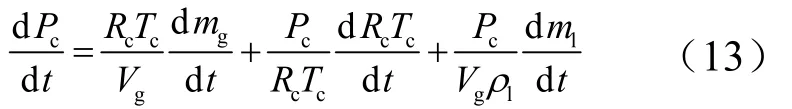
由于催化床内装载着紧密的催化剂,因此推进剂通过催化床时需要克服阻力称为床流阻,床流阻常采用经验公式计算[1]。
1.3 其他组件模型
用于单组元姿控发动机冷起动过程仿真的其他组件,如限流圈流阻模型,电磁阀考虑了阀芯动作过程的Γ-m模型,电磁阀后集液腔考虑气体多变过程的充填排气模型等[17]。限于文章篇幅不再详述。
2 仿真模型的建立及校验
某次单台发动机地面试车考核了发动机在低温下的工作特性,试验系统如图1所示。在该单机地面试验系统中所采用的推进剂为液体单推-3[18](DT-3)。由于试验系统中流量计的采样频率较低,不能反映发动机起动过程中的快速流量变化,故在此以推力室的室压表征单组元发动机的冷起动特性。
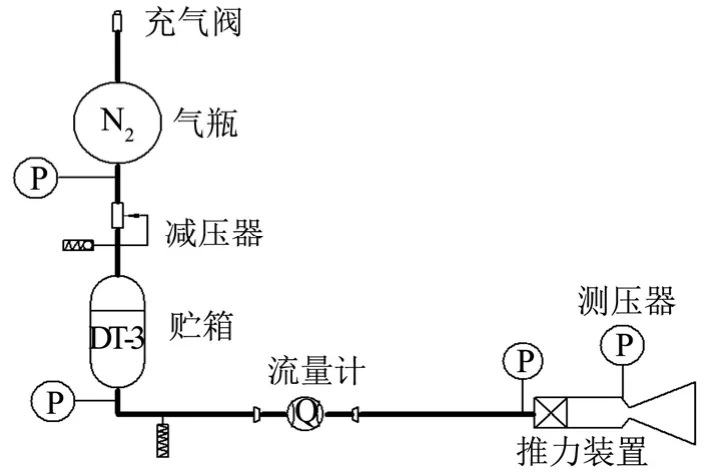
图1 单台发动机地面试验系统示意Fig.1 Engine Ground Test System Schematic
基于第1节所建立的典型组件数学模型,在MWorks软件平台上搭建该型单台发动机的仿真模型,数值计算方法上采用4阶Range-Kutta方法。计算结果和试验测量结果如图2所示。
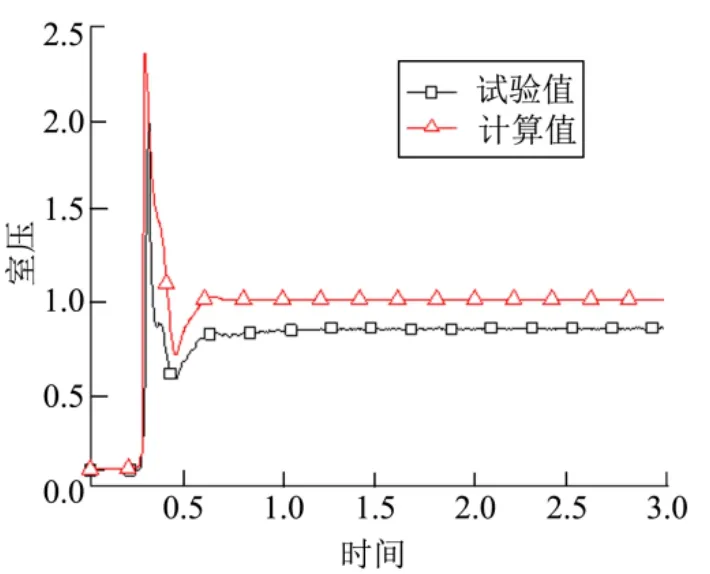
图2 单台发动机冷起动过程仿真与试验结果对比Fig.2 Simulation Results Compare with Ground Test Results of Engine Cold Starting Process
图2中试验值与计算值的比较结果表明,发动机室压的计算值与试验值变化趋势吻合较好,但室压计算值较试验值偏高,引起这一误差的主要原因是计算值是包含了催化床流阻部分的整个催化床平均压力,而试验测量值仅为推力室喷管入口处的压力;并且发动机在冷起动时催化床分解效率是随发动机工作时间逐渐升高的,而仿真中将分解效率设为恒定的稳态分解效率,这2个因素导致了室压计算值较高。其次,计算得到的室压建压曲线相比试验建压曲线更为陡峭,压力峰的计算值稍快于试验值,则是因为催化床模型采用了分解时滞模型反映推进剂的分解过程,认为积存推进剂全部在瞬间发生快速分解,而发动机实际过程中积存的推进剂也是根据进入催化床顺序先后逐步发生快速分解的,同时测量系统可能无法完全捕捉到室压快速上升过程,考虑到这两方面因素从而导致计算建压过程快于试验测量的建压过程。
国外TRW公司对自发型催化剂Shell-405及其单组元肼发动机进行了充分的真空、地面点火试验研究[19],得到了不同初始温度下发动机的冷起动响应时间,但文献中未能给出试验所用发动机系统的具体参数,因此选取起动响应时间作为关注量,起动响应时间指推进剂进入催化床到推力室内压力达到稳态室压的5%所需时间。图3给出了TRW公司地面试验用发动机和本文所研究单组元发动机的冷起动响应时间随初始温度变化的试验值和仿真计算曲线。这里的温度是指推进剂与催化床的初始温度,考虑发动机地面试验时第1次起动的催化剂与推进剂温度相差不大,在此假设这两者温度一致。
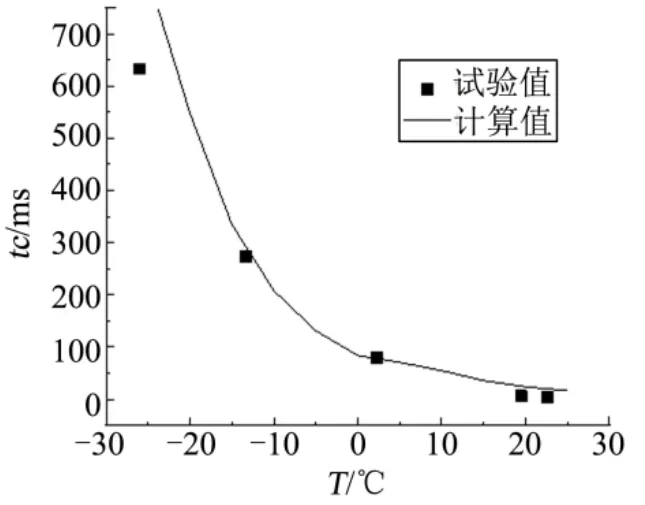
图3 响应时间随初始温度变化对比Fig.3 Comparison of Test Data and Calculated Values of Response Time with Initial Temperature
本文的计算结果与文献19中试验数据的吻合情况较好。在初始温度降至-20 ℃以下时,计算值与文献19试验值的误差有增大的趋势,分析认为是该温度范围接近推进剂的冰点-30 ℃,数学模型中所采用的推进剂物性参数计算公式在该范围内适用性变差所导致。
3 仿真结果分析
3.1 单组元发动机冷起动过程研究
以第2节验证过的仿真模型为基础,以发动机设计温度下的状态参数值为参考,讨论和研究初始温度对发动机冷起动过程中室压和响应时间的影响。图4给出了不同初始温度下发动机冷起动过程中无量纲室压cP随时间的变化。由图4可知,催化床与推进剂的初始温度对发动机的冷起动过程影响较大。初始温度越低,起动响应时间越长,冷起动压力峰越高,发动机的冷起动性能越差,降低了发动机的结构可靠性。还可以看到,在出现冷起动压力峰后压力曲线还会伴随“凹坑”。这种“凹坑”现象的产生是由于高压力峰的存在,使得整个系统压差变化,发动机供应系统出现短暂的推进剂供应不足导致推力室产生了较大的压力波动。冷起动压力峰越高,所产生的压力“凹坑”越突出。在初始温度为10 ℃时冷起动压力峰已经高达设计值的4.5倍左右,并且伴随了更为明显的“凹坑”,压力的最低值已经接近0值而后缓慢爬升至设计稳定值,导致发动机达到稳态工作压力的时间明显延长,严重影响了发动机的工作可靠性。
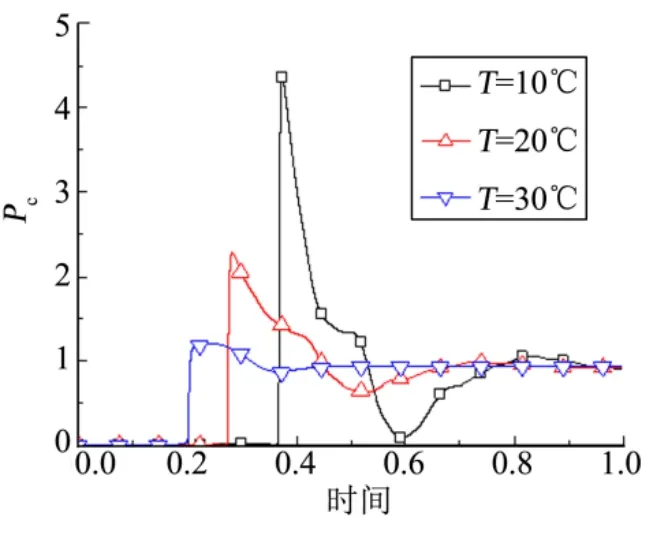
图4 初始温度对冷起动过程的影响Fig.4 Influence of Initial Temperature on Cold Starting Process
进一步模拟不同初始温度下发动机的冷起动过程,图5为初始温度在0~30 ℃推力装置的无量纲冷起动压力峰值及响应时间随初始温度的变化。可以看到,冷起动压力峰值和冷起动响应时间呈现正相关的关系。这意味着冷起动响应越快,冷起动压力峰越低。
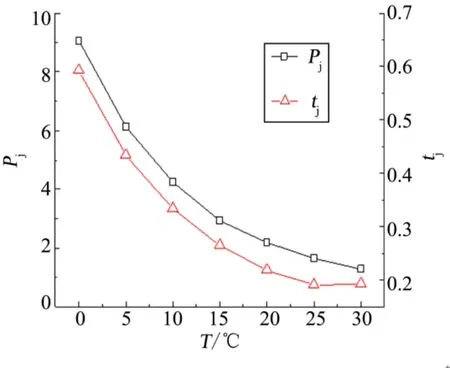
图5 压力峰值及峰值时刻随初始温度的变化Fig.5 Influence of Initial Temperature on Pressure Spike and Response Time
随着初始温度的升高,冷起动压力峰和响应时间随温度的变化近似呈指数变化。对于所研究地面试验系统中的单组元发动机,当催化床和推进剂的初始温度从0 ℃升高到30 ℃时,压力峰值降低了85.8%,响应时间减小了67.5%。催化床和推进剂的初始温度显著影响着单组元发动机的冷起动过程,尤其是在初始温度较低时,即便是较小程度的提高初始温度也可以明显地改善发动机冷起动延迟长、压力峰高的现象。
3.2 初始温度对冷起动延迟的作用机制分析
由冷起动延迟过程分析可知,初始温度主要影响着包括催化分解反应、液相推进剂蒸发以及气相推进剂扩散这3种过程以及液相推进剂的表面张力,为进一步比较分析4种因素对冷起动延迟的影响程度,以20 ℃时各参数值为参照,对式(10)进行无量纲化后再取以为底的对数得到:
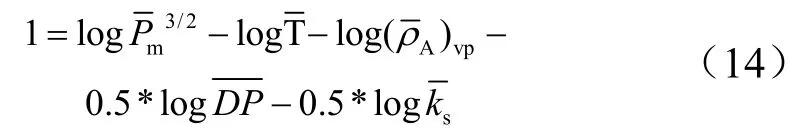
由于log函数不改变原函数的单调性,因此式(14)中右侧分别代表着表面张力、初始温度、饱和密度、气相推进剂扩散系数以及分解反应速率对冷起动延迟时间的影响因子。由于推进剂的冰点为-30 ℃,因此计算初始温度在-20~30 ℃情况下各影响因子的变化如图6所示。
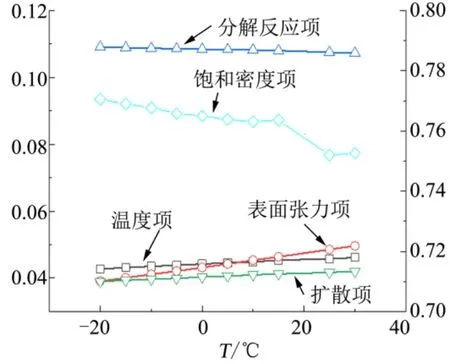
图6 不同初始温度下各项的影响因子Fig.6 Influencing Factors at Different Initial Temperature
由图6可知,随着初始温度的升高,饱和密度项和分解反应项呈现一定的下降趋势,而表面张力、扩散系数和温度3项相应的影响程度逐渐提高。其中表面张力的作用随温度上升提高明显,在大约10 ℃其作用已经超过了扩散系数和温度项的影响,但是这3项的影响因子都小于5%。
在所研究的温度范围内,饱和密度项的影响因子一直处在较高值,并且超过其他4项之和的2倍以上。因此液体推进剂的蒸发过程是单组元肼发动机冷起动过程中导致延迟较长、压力峰较高的主导因素;其次分解反应项的影响因子超过了10%,表明分解反应过程在冷起动过程中的影响也不容忽略。
3.3 不同推进剂的冷起动温度敏感性
肼-70、无水肼和DT-3是3种常用肼类单组元推进剂[16,20],本节讨论相同条件下采用不同推进剂的单组元发动机冷起动特性。图7为采用3种推进剂的发动机在-15~30 ℃初始温度条件下的冷起动延迟时间。由图7可知,在所计算温度范围内,无水肼发动机冷起动延迟最长,且随初始温度的降低,冷起动延迟的差距愈加明显,-15 ℃时无水肼和DT-3的差值已达到1倍以上。考虑3.1节得到的冷起动压力峰与冷起动延迟时间正相关,故认为采用DT-3的单组元发动机在相同条件下较无水肼和肼-70具有更好的冷起动特性。
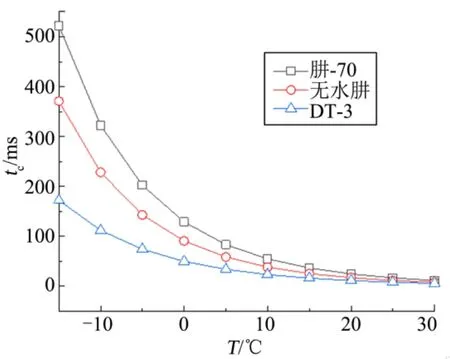
图7 冷起动延迟时间随初始温度变化Fig.7 Influence of Initial Temperature on Response Time of Cold Starting
4 结 论
本文建立了反映冷起动延迟的单组元姿控发动机典型组件数学模型,分析了单组元姿控轨发动机在不同初始温度下的冷起动特性,得到以下结论:a)单组元姿控发动机冷起动过程仿真模型的计算值与试验值吻合较好,冷起动延迟时间与文献中试验值趋势相同,验证了所建立催化床冷起动延迟数学模型和相应仿真模型,可为工程设计提供理论支持。b)肼类单组元发动机冷起动过程中压力峰与起动延迟正相关,并都与初始温度近似指数变化的关系。c)相比于低温下气态推进剂的扩散过程和催化分解过程,液体推进剂进入催化床后的蒸发气化过程是单组元发动机在较低温度起动时延迟长、压力峰高的主导因素。
相较于肼-70和无水肼,采用单推-3的单组元催化分解发动机具有更好的冷起动特性。

