重复使用运载器着陆滑跑距离估算方法研究
朱如意,王 征,张春阳,张月玲
(中国运载火箭技术研究院,北京,100076)
0 引 言
重复使用运载器在再入返回着陆后要经历地面滑跑段直至停机。地面滑跑段是飞行任务剖面重要的组成部分。对于重复使用运载器而言,其再入返回着陆时滑跑距离的长短不仅反映飞行器的性能水平,同时也影响其他一些因素,比如着陆场选择或设计、是否使用减速伞、控制系统设计、起落架系统设计等。着陆场跑道的高度会影响滑跑距离的长短,在其他条件不变情况下,着陆场跑道高度越高、着陆速度越大,滑跑距离越长;着陆场跑道高度越低、着陆速度越小,滑跑距离越短,对起落架轮胎的使用寿命越有利,对于可重复使用的飞行器而言是利好因素。地面滑跑距离是飞行器着陆性能中最主要的指标之一,良好的着陆性能对飞行器的安全着陆至关重要。为了满足滑跑距离的要求,需要研究是否使用减速伞以缩短滑跑距离,是否优化起落架刹车装置,是否优化控制系统设计,这些因素相关联,进而影响的是飞行器总体设计。
目前,滑跑距离的计算或者分析诸多见于飞机,涵盖飞机起飞滑跑距离和跑道长度、发动机推力计算等,邓杨晨等[1]通过优化方式给出了发动机的最佳安装角和飞机地面滑跑的最佳攻角及前起落架的最佳凸伸量,并确定了飞机地面滑行过程中的最短滑跑距离;宋花玉等[2]应用人工神经网络技术对飞机起飞滑跑距离进行了研究,给出了基于BP网络的飞机起飞滑跑距离计算模型,并对飞机实际滑跑距离及其影响因素进行了归一化处理;张志刚等[3]针对MA60飞机进行了高原机场起飞性能研究,结合MA60飞机的特性,计算出起飞滑跑距离等参数值;在发动机推力计算和滑跑长度计算方面,宋花玉[4]利用数值理论计算了飞机起飞滑跑距离,研究了发动机瞬时推力的确定方法,提出以发动机推力曲线为基础,通过拉格朗日插值确定未知推力的算法;黄文静等[5]针对装有反推力装置的某型飞机,给出了着陆滑跑距离向标准条件换算的方法。许震宇等提出了地效飞行器或水上飞机水面起飞滑跑距离估算方法,在基本运动方程中引入了机身浸湿面积与滑行速度成负斜率线性关系的假设,简化起飞距离的计算过程,得到发动机推力与起飞滑行距离之间的关系曲线[6]。航天飞机不同架次着陆滑跑距离统计数据可见公开文献[7],但未涉及滑跑距离计算方法。对重复使用运载器、无动力再入飞行器滑跑段模型研究还比较少,对滑跑距离方法研究也比较少。
重复使用运载器再入及滑跑段无动力,受气动力、风、减速伞一系列因素影响,单纯应用飞机着陆的经验公式,不足以准确估算飞行器滑跑距离。本文提出一种简单易懂的滑跑距离估算方法,在跑道坐标系下建立飞行器着陆滑跑估算模型,考虑减速伞和地面风影响,研究不同滑跑工况下的滑跑距离估算方法。该滑跑距离估算方法简洁、算法易实现,适合工程应用。
1 滑跑距离估算模型
可重复使用运载器地面滑跑时的实际运动是一种复杂的现象,为了使计算尽量简单而不失准确性,需要进行简化假设。在建立着陆滑跑估算模型时与绝大部分模型一样,将飞行器视为理想刚体,忽略机体弹性振动的影响。
因为本文的滑跑距离估算采用简化算法,是沿着跑道方向开展滑跑距离估算,故选择在跑道坐标系下建立着陆滑跑估算模型,着陆场跑道坐标系OdXdYdZd见图1。飞行器着陆滑跑时飞行器受力状态如图2所示。
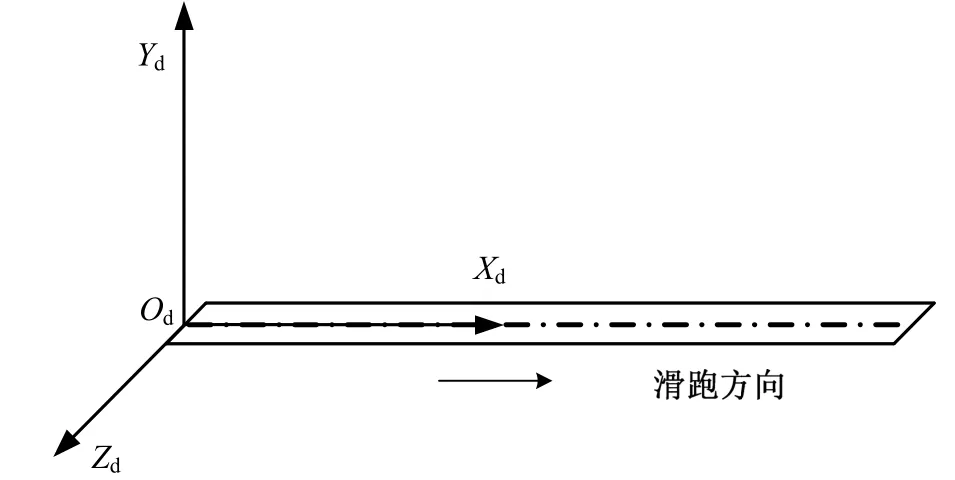
图1 着陆场跑道坐标系Fig.1 The Runway Reference Frame
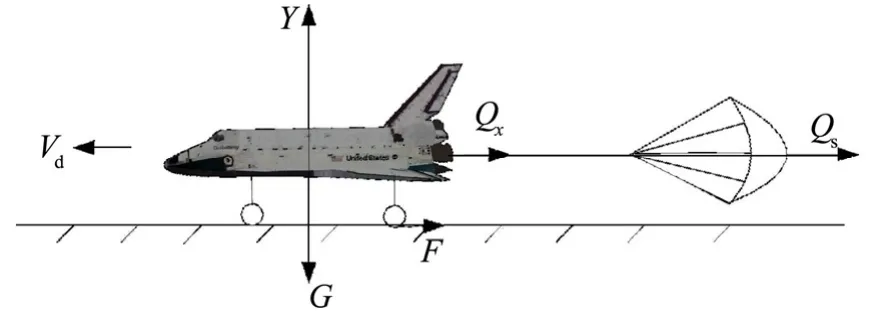
图2 飞行器受力状态Fig.2 The Force State of the Aircraft
减速伞张满后飞行器着陆滑跑运动方程为
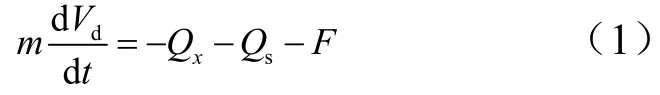
式中m为飞行器总质量;Vd为地速;Qx为气动阻力;Qs为阻力伞拉力;F为地面作用在飞行器上的摩擦力和刹车阻力。
考虑地面风的影响,有:
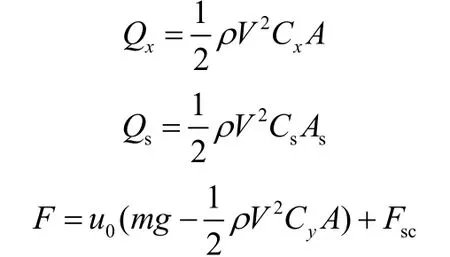
式中Cx,Cy为滑跑时气动阻力、气动升力系数;CsAs为减速伞特征值;u0为滚动摩擦系数;ρ为着陆场空气密度;A为机翼参考面积;Fsc为主轮刹车所产生阻力;V为空速。地面风会影响动压,设定Vw为风速,则有:
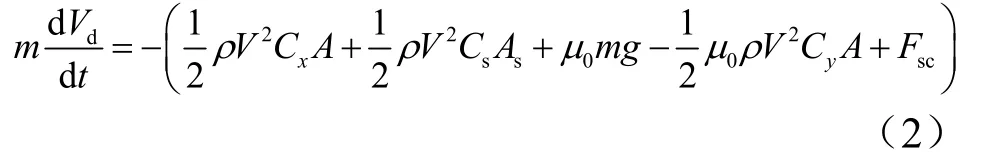
令:
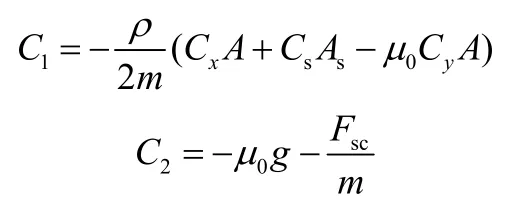
则式(2)可以写成:

由于
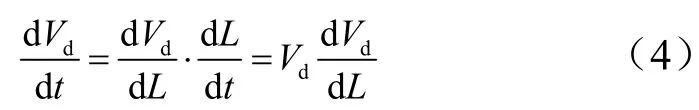
式中L为伞张满后滑跑距离;顺风时Vd=V+Vw,逆风时Vd=V-Vw,本文以顺风为例。
联合式(3)得:
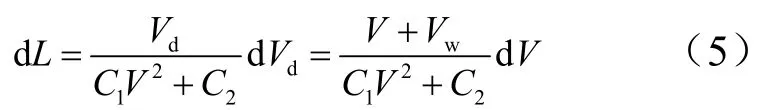
对式(5)积分后得:
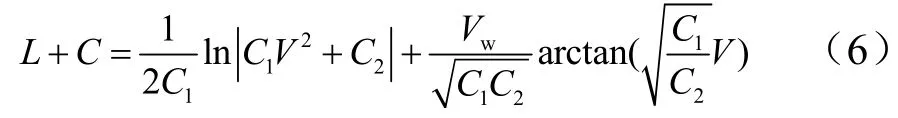
伞开始张满时速度为VM(空速),对应滑跑距离L=0,因此可得:

则得:

2 滑跑距离估算方法
2.1 正常滑跑工况
开伞到伞张满时段,为简化分析,近似认为飞行器匀速滑跑,滑跑距离为

式中tM为该时段时长。
伞张满到开始刹车时段,飞行器滑跑距离为
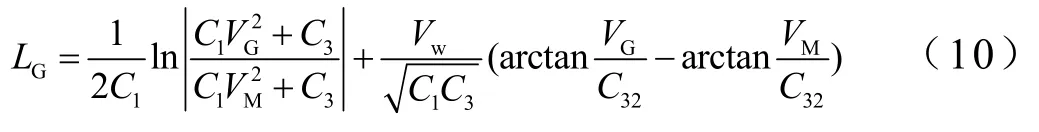
式中GV为刹车时刻的空速;。
开始刹车到抛伞时段,滑跑距离为
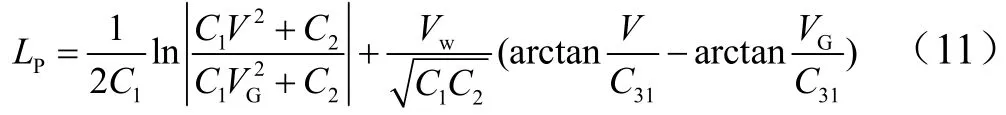
抛伞后滑跑过程中,当飞行器速度达到顺风风速时,空速为零,此后飞行器不受气动阻力、升力以及减速伞的作用力,水平方向只有摩擦力、刹车产生的阻力作用。
抛伞到飞行器达到风速时段,滑跑距离为
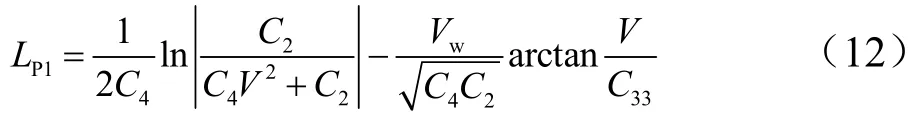
从空速为零到停机时段:
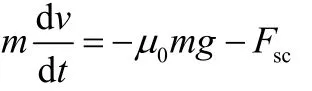
从空速为零到停机的滑跑距离为
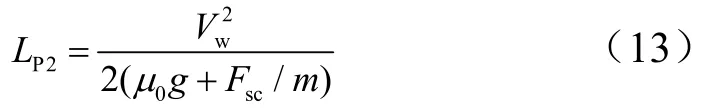
则从开伞到停机的滑跑距离为
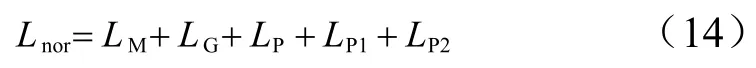
2.2 用伞无刹车工况
伞张满到抛伞时段,飞行器滑跑距离为
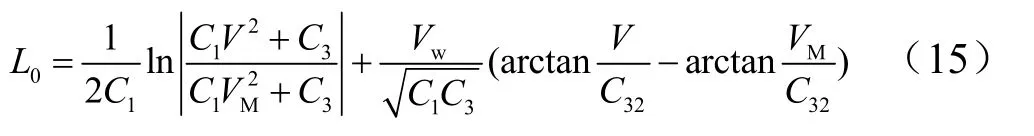
抛伞后滑跑过程中,当飞行器速度达到风速时,空速为零,此后飞行器不受气动阻力、升力以及减速伞的作用力,水平方向只有摩擦力作用。
抛伞到飞行器达到风速时段,滑跑距离为
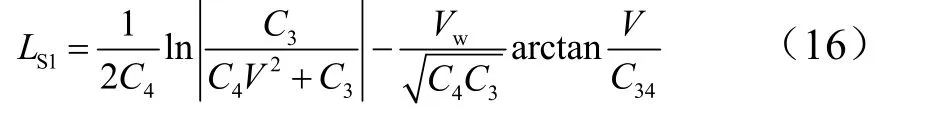
从空速为零到停机时段:
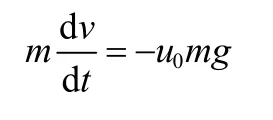
从空速为零到停机的滑跑距离为

则从开伞到停机的滑跑距离为
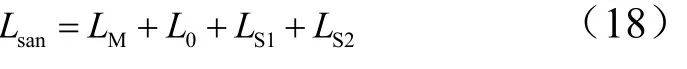
2.3 刹车不用伞工况
为简化分析,开伞到开伞失败信息反馈过程,近似认为飞行器匀速滑跑,滑跑距离为

式中tsb为开伞到开伞失败信息反馈时间;V1为该时段的滑跑速度。
开伞失败后开始刹车,当飞行器速度达到风速时,空速为零,此后飞行器不受气动阻力、升力作用,水平方向只有摩擦力、刹车产生的阻力作用。
开始刹车到飞行器达到风速时段,滑跑距离为

式中VG0为该工况下的开始刹车速度(空速),不同于正常滑跑时开始刹车速度。
从空速为零到停机时段:
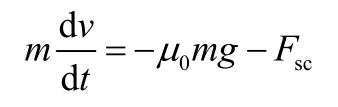
从空速为零到停机的滑跑距离为
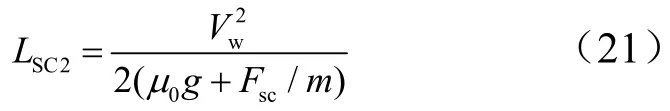
则从开伞(失败)到停机的滑跑距离为

3 结束语
重复使用运载器滑跑段无动力,受气动力、风、减速伞等一系列因素影响,运动规律较复杂。本文侧重从工程应用和初期总体设计的角度,提出一种简单易懂的滑跑距离估算方法,在跑道坐标系下建立飞行器着陆滑跑估算模型,考虑减速伞和地面风影响,研究不同滑跑工况下的滑跑距离估算方法。该估算方法简洁、算法易实现,适合工程应用。

