比例导引律在空间交会中的应用研究
0 引 言
交会对接的制导控制一直是空间技术领域的研究热点。国内外有大量文献对空间交会的制导控制进行了研究[1~3],其中大多基于动力学规律对飞行器进行预测和控制,控制效果较好,但其对导航设备的精度要求较高,需要克服惯性器件误差的累积效应。
比例导引是一种基于运动学规律进行轨道控制的闭路制导控制方法,它使飞行器速度向量的旋转角速度与目标视线的旋转角速度成正比,以达到消除视线转率的目的,从而实现对目标的准确拦截[4,5]。由于视线参数测量相对简单,对惯性器件精度要求不高,且易于工程实现,因而在目标拦截领域得到广泛应用[6,7]。文献[8]和文献[9]开展了比例导引律在大气层外拦截器应用的研究,由于与空间交会过程不同,并未考虑近距离减速制动过程的制导律设计。文献[10]采用比例导引方式实现了空间交会控制,但在交会末段出现了视线角速度剧烈变化的现象,轨控发动机频繁开启。
本文对比例导引应用于空间交会进行研究,针对匀速接近段和减速制动段分别提出了适应固定推力的比例导引律,实现了较高的交会精度,有效减少了交会末段发动机开启次数和燃料消耗,并对非机动目标和机动目标的适应性进行了仿真分析。本文研究的追踪器安装4台轨控发动机,可提供垂直于视线的4个方向的控制力,且推力为常值,可多次启动。
1 相对运动动力学方程
首先定义视线坐标系Oξηζ。原点O位于追踪器质心,Oξ轴与视线方向重合,Oη在轨道平面内与Oξ轴垂直,Oζ轴垂直于Oξη平面。
设rM、rT分别表示追踪器和目标的地心矢量,r表示追踪器指向目标的相对矢量,r=rT-rM。追踪器的相对运动矢量方程为
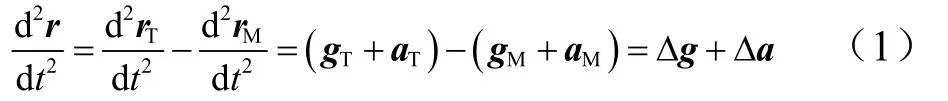
式中 Δg为作用在目标和追踪器上的引力加速度差。由于追踪器和目标间的距离相对地心距为小量,引力差为小量,且交会过程的时间较短,可忽略其对相对运动的影响,将Δg项略去;Δa为作用在目标和追踪器上的控制加速度差。不考虑目标机动时,ΔaT=0,则Δa=ΔaM。
设视线坐标系相对于惯性坐标系的转动角速度为ω,其在视线坐标系上的3个分量分别为ωξ、ωη和ωζ,即ω=(ωξωηωζ)T。视线方向的角速度ωξ近似为零。矢量形式的相对运动动力学方程为
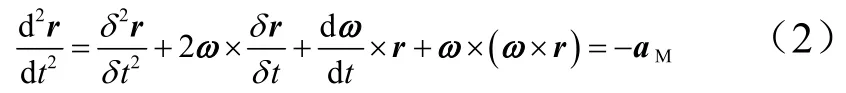
式中r=(r0 0)T。追踪器的控制加速度在视线坐标系的表示为aM=(aξ aη aζ)T。
式(2)可化简为标量形式的相对运动动力学方程:
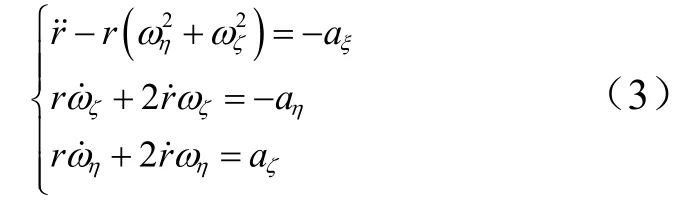
不进行控制时,aξ=aη=aζ=0,对后两式积分可得:
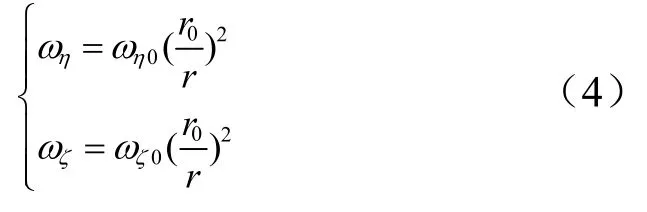
可见,如果对追踪器不施加控制,视线角速率将随着相对距离r的减小而不断增大,无法满足比例导引视线角速率收敛的要求。
2 比例导引律设计
将整个交会过程分为匀速接近段和减速制动段。在匀速接近段追踪器以某固定速度向目标接近,当小于某距离时转入减速制动段,开启反向推力发动机,将追踪器速度迅速减小,直至满足对接要求为止。下面对两个工作段的制导方式分别开展设计。
2.1 匀速接近段
由式(3)可得比例导引控制加速度为

式中K为有效导引比。当K>2时,视线角速度与角加速度反号,可满足比例导引角速度收敛条件。
式(5)为发动机推力可任意变化的比例导引控制方程,而实际情况下轨控发动机提供的推力是常值,比例导引不能直接使用。需要对固定推力比例导引进行研究。
比例导引的思想在于抑制视线的旋转,如果利用比例导引确定发动机的开启和关闭,将交会过程中的视线角速率控制在较小的范围内,也可以达到与比例导引相近的效果。
首先研究利用比例导引确定发动机开启控制线。将式(5)代入式(3),得到:
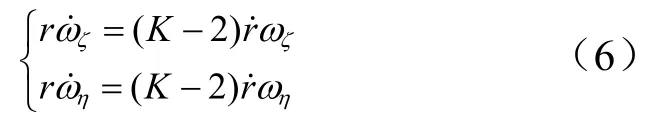
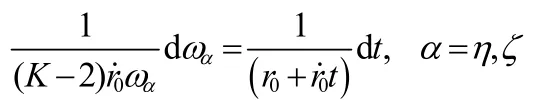
积分得到:
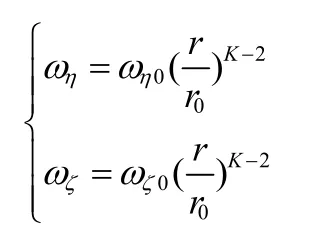
发动机开启控制线为
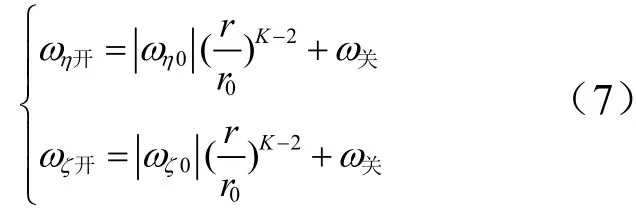
式中ω关>0,为发动机关闭控制线,可由导引头测量灵敏度确定;ωη0和ωζ0为初始视线角速度。可见,K>2时,利用上式得到的发动机开启控制线随着距离r的减小而持续收敛,直至与发动机关闭控制线一致。K值越大,收敛越快。通过对发动机进行开关控制,可将对应的角速度控制在开启控制线和关闭控制线之间的区域,达到抑制视线旋转的目的。K=2是临界状态。当K<2时,无法实现角速度收敛的目的。
上述控制方式存在一个问题,随着追踪器和目标距离的逐渐缩小,开启控制线和关闭控制线也将逐渐接近,导致轨控发动机频繁开关。为了避免该现象,提出一种调整开启控制线终值的方法。在保证制导精度的前提下,将开启控制线的收敛终值从ω关处适当增加至ω开end,使得ω开end>ω关。则发动机开启控制线变为
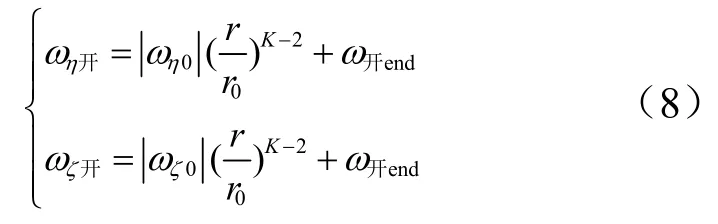
采用非线性开关函数实现对发动机开关的控制,如图1所示。
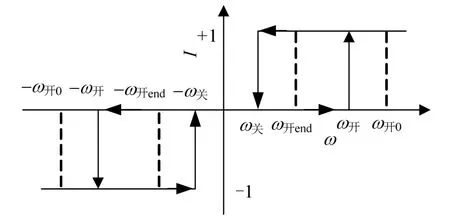
图1 发动机非线性开关函数Fig.1 Nonlinear Switch Function of the Engine
函数表示方式如下:

I-1表示上一控制周期的发动机开关指令。使用此控制方式可以将视线角速度控制在(ω关,ω开)或(-ω开,-ω关)区间内,而ω开在交会过程中从初值ω开0随着距离缩短逐渐缩小至ω开end,实现了抑制视线旋转的作用。
2.2 减速制动段
在减速制动段,为满足对接要求,追踪器进行减速制动,速度逐渐减小至1 m/s以下。由式(3)后两式可知,由于ηω和ζω在匀速接近段已收敛为小量,则在减速制动段存在如下近似公式:

由于控制加速度aη和aζ为常值,由式(9)可知,在进入减速制动过程后,速度减小的同时距离r也将不断减小,角速度变化率将逐渐变大。控制加速度在一个控制周期内就足以使角速度产生较大变化,导致角速度将突破(ω关,ω开)或(-ω开,-ω关)的预期区间,而在(ω开,+∞)和(-∞,-ω开)两个区间频繁反复跳动,且随着r减小呈发散趋势。由于这一阶段速度较小,发散过程将持续较长时间,这对末段逼近对接是很不利的。
为解决上述问题,这里提出发动机开启控制线按照控制加速度确定,并随速度调整的方式,由式(5)得到发动机开启控制线:
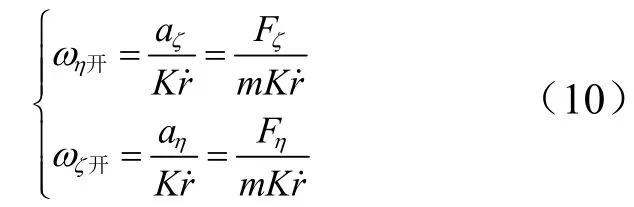
式中Fη,Fζ为对应方向的发动机推力值;m为追踪器质量,均为已知量。
在进入减速制动段后,通过上式控制轨控发动机的开启,即可保证在角速度偏差达到控制加速度能力门限时再开启发动机,充分利用控制加速度实现对角速度的收敛控制,避免出现发动机的频繁开启和角速度的反复跳动,同时保证交会精度。
3 仿真分析
为了验证设计结果的有效性,引入瞬时交会偏差的概念。瞬时交会偏差是指追踪器和目标以当前时刻的状态保持匀速飞行,在交会过程中,追踪器与目标之间的最小距离[9]。
3.1 匀速接近段仿真分析
分别选择表1中不同的初始状态,针对表2是否调整开启控制线收敛终值2种控制方式进行仿真分析。仿真参数ω关=0.001 (°)/s,4K=,不考虑减速制动段,在距目标200 m处计算瞬时交会偏差。仿真结果见表3。
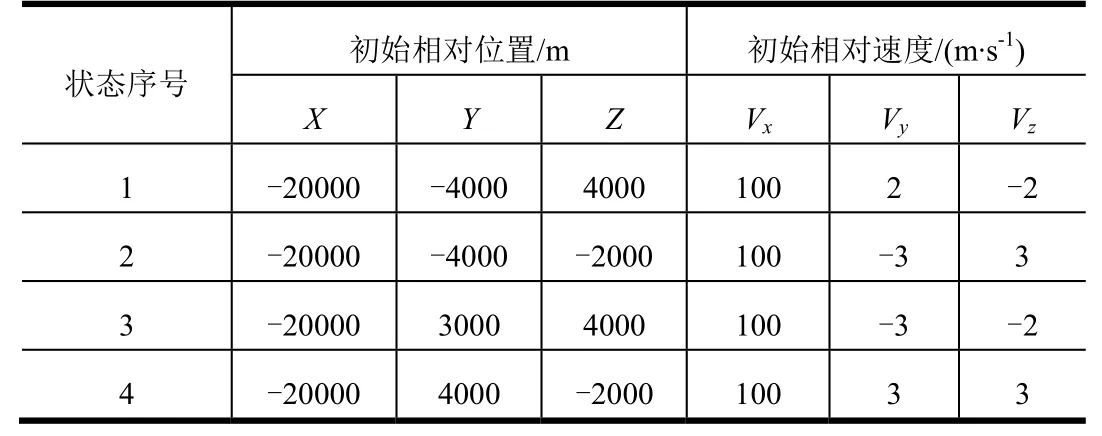
表1 仿真初始状态Tab.1 Initial State of Simulation
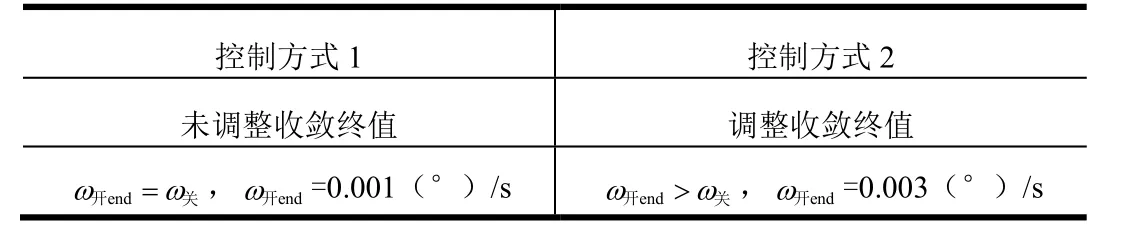
表2 匀速接近段控制方式Tab.2 Control Mode for Uniform Approach Stage
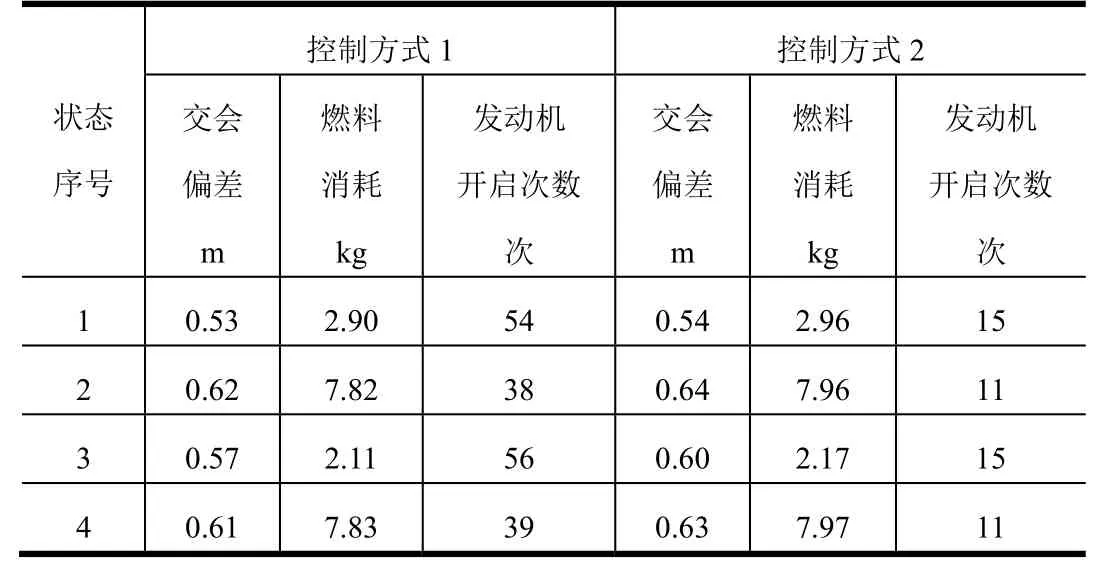
表3 匀速接近段两种控制方式的仿真结果比较Tab.3 Comparison of the Simulation Results between Two Control Mode for Uniform Approach Stage
以状态1为例,匀速接近段视线角速度和对应的发动机开关情况如图2、图3所示。图2对应控制方式1,图3对应控制方式2。从仿真结果可以看出,两种方式均实现了视线角速度的收敛控制,视线角速度控制在(ω关,ω开)或(-ω开,-ω关)区间,交会偏差较小,燃料消耗量基本相当。未调整收敛终值的状态,发动机在匀速接近段后期频繁开启。调整收敛终值后,发动机开启次数显著减少。
显然,调整收敛终值的控制效果更优,后续仿真分析过程的匀速接近段均采用此方式进行控制。
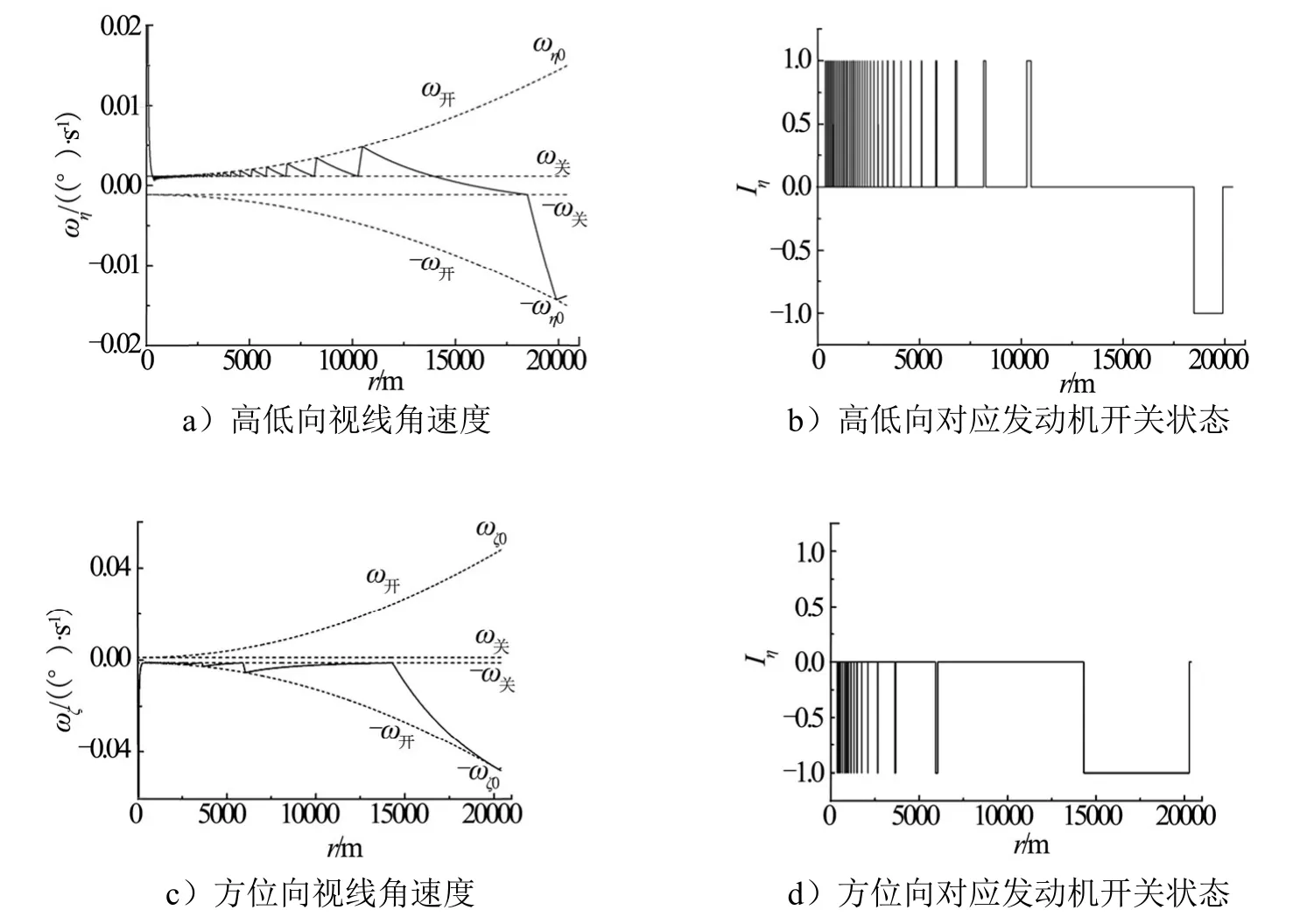
图2 匀速接近段控制方式1视线角速度和发动机开关情况Fig.2 Sight Rate and Engine Status of Control Mode 1 for Uniform Approach Stage
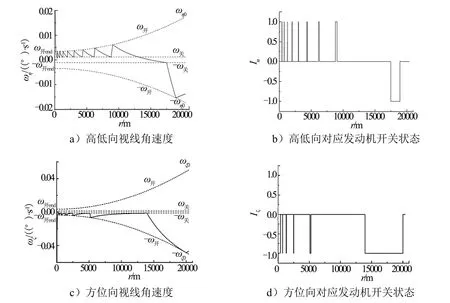
图3 匀速接近段控制方式2视线角速度和发动机开关情况Fig.3 Sight Rate and Engine Status of Control Mode 2 for Uniform Approach Stage
3.2 减速制动段仿真分析
分别选择不同的初始状态,减速制动段按照是否随速度调整开启控制线两种方式进行仿真分析(见表4)。在距目标200 m处转入减速制动段,交会终端相对速度为0.5 m/s。仿真结果见表5。
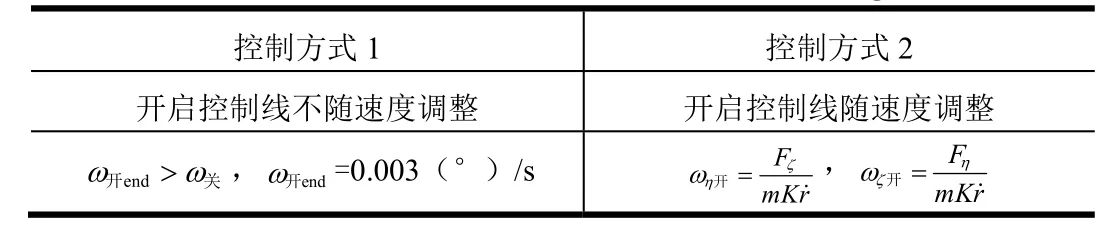
表4 减速制动段控制方式Tab.4 Control Mode for Deceleration Stage
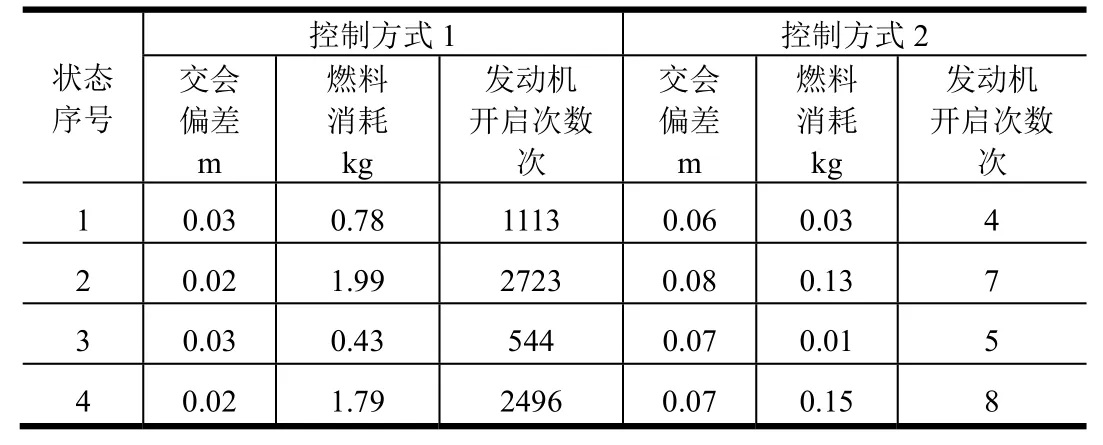
表5 减速制动段两种控制方式的仿真结果比较Tab.5 Comparison of the Simulation Results between Two Control Mode for Deceleration Stage
以状态1为例,减速制动段视线角速度和对应的发动机开关情况如图4、图5所示。
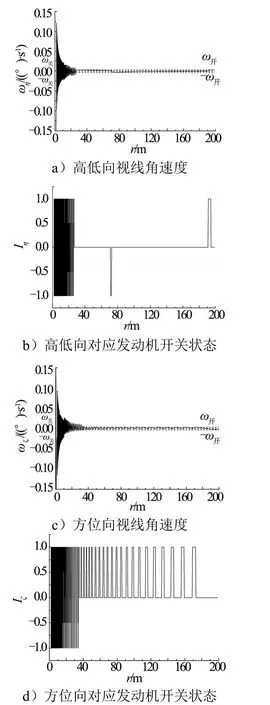
图4 减速制动段控制方式1视线角速度和发动机开关情况Fig.4 Sight Rate and Engine Status of Control Mode 1 for Deceleration Stage
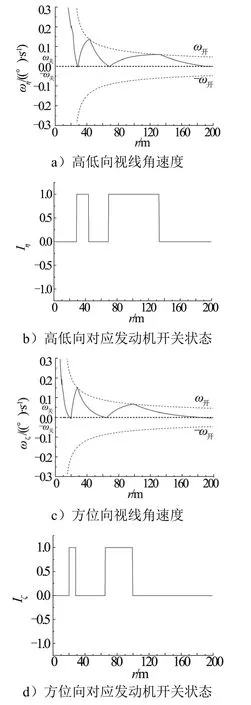
图5 减速制动段控制方式2视线角速度和发动机开关情况Fig.5 Sight Rate and Engine Status of Control Mode 2 for Deceleration Stage
从仿真结果可以看出,在减速制动段采用与匀速接近段相同的控制方式,将导致轨控发动机的频繁开启,角速度随距离的减小呈发散趋势。改进后的制导方式,开启控制线随速度实时调整,轨控发动机开启次数和燃料消耗均显著减少,交会精度保持了较高的水平。
3.3 对机动目标的适应性仿真分析
上述的分析和仿真过程中均未考虑目标机动,而实际应用中,目标是有可能机动的。由比例导引原理和式(5)可知,如果要满足比例导引收敛条件,追踪器的控制加速度应大于目标的机动加速度,且加速度差应满足如下条件。
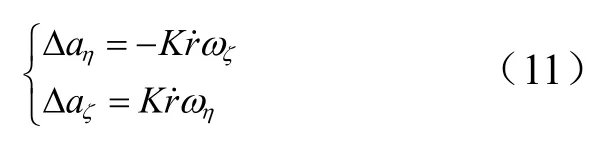
式中aηΔ和aζΔ为视线坐标系2个方向上的加速度差。
本仿真模型中,追踪器产生的控制加速度为0.3 m/s2,目标机动加速度按照最大为0.15 m/s2进行仿真。针对目标2种机动形式开展仿真分析:a)目标做直线加速机动:aTy=aTz=0.15 m/s2;b)目标做三角波机动:aTy=aTz=0.15sin(0.1t) m/s2。其它仿真条件同状态1。仿真结果见表6。

表6 对机动目标的适应性仿真结果Tab.6 Adaptability Simulation Results for Maneuverable Target
从仿真结果可知,本文所提出的制导方式对机动目标的适应性较好,仍可以保证较小的交会偏差。燃料消耗和发动机开启次数相对目标无机动状态,存在明显增加,这是由于跟踪目标过程中,追踪器需要根据目标机动状态不断调整跟踪方向所致。
4 结 论
本文对比例导引应用于空间交会问题进行了研究,提出一种适应固定推力的比例导引律,对非机动目标和机动目标均有良好的制导效果。通过对发动机开启控制的优化设计,在保证较高制导精度的同时,显著减少了发动机开启次数和燃料消耗。

