再入式飞行器不同绕流状态的底部流动特征

刘丽丽，陈培芝，赵 月，朱德华

（1. 中国运载火箭技术研究院，北京，100076；2. 中国航天空气动力技术研究院，北京，100074）

0 Introduction

Re-entry vehicles such as return capsules and warheads have flight stability problems. The stability characteristics of bottom flow are one of the key factors influencing the stable flight of re-entry vehicles, since the instability of bottom flow will generate non-constant oscillation aerodynamic forces, which will cause non-constant vibration of the vehicle.

Since the numerical simulation of bottom flow of re-entry vehicle faces complex physical phenomena such as separation and rotation, the classical numerical simulation methods often cannot accurately obtain the bottom flow instability characteristics. In the wind tunnel test, the support mechanism is required for the test model, and the model support has a great impact on the bottom flow instability characteristics, which can cause distortion of the bottom flow physical phenomena. Therefore, there has been a lack of theoretical understanding and bias in the observation of bottom flow instability phenomenon and the cognition of instability mechanism.

In recent years, with the improvement of numerical simulation capability and wind tunnel test technology,people started to explore the characteristics of bottom flow of re-entry vehicles again. In wind tunnel tests, Herrin and Dutton[1]analyzed the complex flow structure in the near wake region of a supersonic bottom flow field with Mach number 2.5; Bourdon and Dutton[2]obtained images of the transient flow in the near wake region of a supersonic bottom flow field using planar laser imaging; Danehy and others used planar laser-induced Danehy[3,4]studied the bottom flow characteristics of the return capsule using the technique of planar laser-induced fluorescence and found that laminar, turning, and turbulent morphological features exist in the shoulder shear layer of the return capsule and have an impact on the bottom flow. Similar experimental studies of bottom flow with blunt body shape have been done by Gregory[5], Nishio[6], etc., whose experimental measurements are aimed at understanding the bottom flow characteristics. In terms of numerical simulation, high-precision numerical simulation methods are the main research tools for bottom flow characterization. Matthew MacLean[7]et al. performed numerical calculations of laminar and turbulent flow states for the return capsule shape, using the DES method in the US3D code, and obtained the model surface pressure and heat flow information for different flow states and compared them with experiments. Shingo Matsuyama, et al.[8]performed numerical simulations using the Large Eddy Simulation (LES) method for the Mars entry module shape, revealing that the bottom flow stability study is affected by the mesh sparsity, calculation method, and flow state; Brock[9]et al. performed numerical simulations of the bottom flow of the high-speed return module using the RANS and RANS/LES methods, and obtained the numerical results of laminar to turbulent flow at the bottom of the return capsule. There are also some representative works for numerical simulation of bottom flow of blunt body shape such as Datta[10], Sandberg[11], Sivasubramanian[12], Simony[13], Zhu De-Hua[14], Xiao Zhi-Xiang[15]and so on. The study of the flow wake region at the bottom of the blunt body bypass is also one of the hot spots, and Tu Jia-Huang et al[16,17]have made some progress in the study of wake disturbance in cylindrical and square column bypasses at low velocity and low Reynolds number scenarios; Gong Sheng and Wu Chui-Jie[18]carried out a large eddy simulation study on the effect of the wake of the Mars entry module on the parachute system.

In summary, the study of bottom flow stability of re-entry vehicle bypass flow has certain difficulties both in wind tunnel tests and numerical simulations, and the phenomenon of bottom flow instability and the instability mechanism still have theoretical understanding deficiencies and deviations. With the advancement of high-precision numerical simulation methods and the improvement of massively parallel computing capabilities, it has become possible to recognize the bottom flow characteristics of such blunt body bypass flows.

In this paper, a multi-zone parallel large eddy simulation method will be used to study the bottom flow characteristics of the Shenzhou-like return module shape under low and high Reynolds number re-entry conditions, which will provide some basic theoretical support for the re-entry vehicle shape design, stability control and wake disturbance research.

1 Control Equations and Numerical Methods

The control equation is a three-dimensional compressible Navier-Stokes equation in a curved coordinate system[19], which is solved by a high-precision multi-zone parallel implicit large eddy simulation method based on finite differences. For the spatial discretization, the fifth-order WENO format[20]is used for the inviscid term and the sixth-order central difference is used for the viscous term. The third-order TVD Runge-Kutta method[21]was used for the time discretization.

The isothermal no-slip boundary condition is used at the wall, the singularity axis is treated by circumferential averaging and the far field is a reflection-free boundary condition. In addition, for the inviscid term treatment, the singularity axis is downscaled to NND format in the axial direction[14].

2 Analysis of Calculated Results

The calculation conditions were chosen with reference to the experimental conditions of Brock[9]et al. The specific computational conditions are (Re with 1 m as the characteristic length):

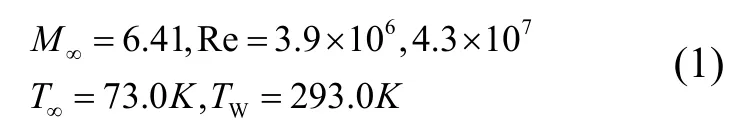
The computational model is selected as a scaled-down Shenzhou-like return module with the following dimensions: in Fig.1.

Fig.1 Dimensional Diagram of the Computational Model(unit mm)

In this paper, the basic flow pattern of high-speed winding based on the Shenzhou-like shape is initially given to provide some theoretical support for the subsequent numerical simulation study. The basic flow around shape in shown in Fig.2.

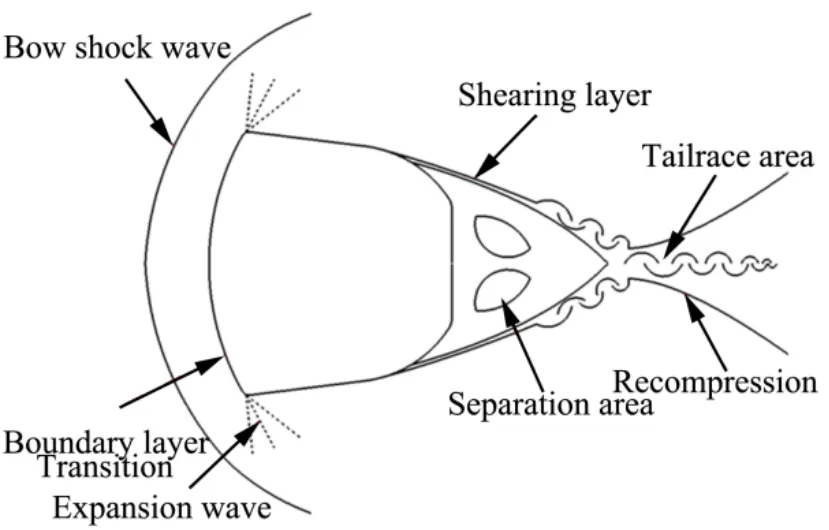
Fig. 2 Basic Flow Around Shape of Return Module Shape

Based on the above basic flow pattern of high-speed blunt bypass flow, a structural grid is selected to carry out high-precision numerical simulation work. The Shenzhou-like return capsule shape has axisymmetric characteristics, so it is suitable to choose a mixed method of C-grid and H-grid to realize the local encryption of the grid in the complex flow region. In order to ensure the simulation accuracy of the boundary layer, the grid scale of the first layer at the wall is 10 μm, y+wall = 0.8, and the grid volume is about 40 million. The schematic diagram of the Shenzhou-like return module mesh for local grid encryption of the complex flow region is shown in Fig.3.

Fig. 3 Schematic Diagram of Shenzhou-like Shape Grid

2.1 Bottom Flow Instability Characteristics under Different Reynolds Number Conditions

The winding characteristics of the high-speed re-entry vehicle are similar to the typical high-speed blunt body winding characteristics, and the main physical phenomenon appearing in its head region is the debris surge. The Fig. 4 shows the pressure cloud diagram on the surface of the class Shenzhou return capsule shape, and it can be seen that the pressure distribution on the object surface shows an axisymmetric pattern, and the symmetry of the head is maintained well as the calculation time advances. The main physical phenomenon appearing in the bottom region is flow separation, which is essentially structural instability in the Reynolds number range chosen in this paper, and asymmetric structural instability will occur in the presence of perturbations, with periodic as well as non-periodic structural oscillation characteristics. The main physical phenomenon occurring in the shoulder region is the shear layer. The centrosymmetric surface in the figure below is shown using density gradient in order to show the wave system structure and the stability characteristics of the shoulder shear layer in the bottom flow region. The comparison between Fig.4a and Fig.4b shows that the shear layer in the high Reynolds number state is destabilized earlier and the recompression wave intensity in the wake area is stronger. The main physical phenomena occurring in the wake development zone as well as the far wake zone are transitions, turbulence, and Karman-like vortex streets. The vortex structure in the figure below is shown with the second invariant Q value of the velocity gradient. It can be seen that both high and low Reynolds number state trailing areas appear the vortex structure, and the high Reynolds number state trailing vortex structure appears earlier and has obvious oscillation characteristics.

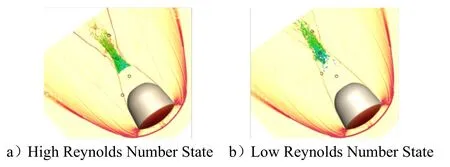
Fig. 4 The Transient Flow Structure and Monitoring Point Distribution of the Return Module Shape Winding Flow

In summary, the Shenzhou-like return module bypass flow obtained by numerical simulation is consistent with the basic characteristics of high-speed blunt body bypass flow. The black circles in Fig.4 show the pressure signal monitoring points, which will be used for detailed quantitative analysis of the formation mechanism of the bottom flow characteristics in the following.

2.1.1 Similarities and Differences in the Instability Characteristics of the Bottom Flow Structure

The monitoring point 1 in Fig.4a is arranged to analyze the oscillation characteristics of the bottom separation region, and the selected position is near the line between the bottom object surface half-saddle point S' and the re-attached saddle point S on the central symmetry plane, and the monitored pressure signal is the distribution of the dimensionless pressure with the arbitrary dimensionless time (t=¯t/(L/u∞), whereLis the characteristic length of 1 m) interval as shown in the Fig.5. From Fig.5, it can be seen that the pressure oscillation is obvious in the high Reynolds number state, and its periodic characteristics are disturbed to some extent by the shear layer instability.

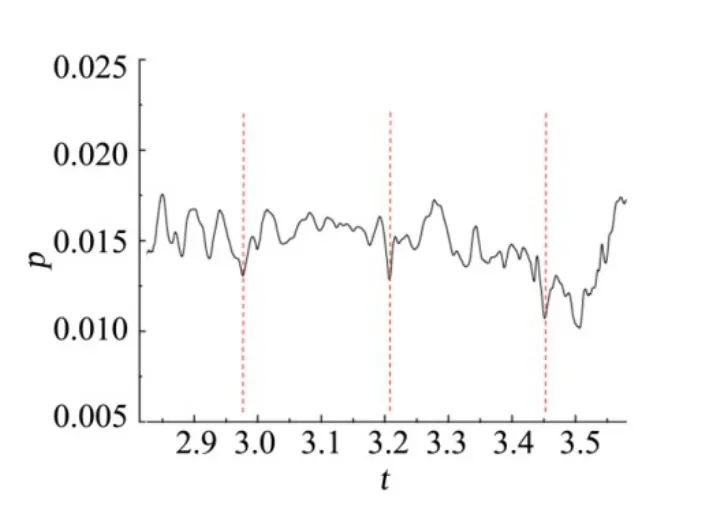
Fig.5 Pressure Distribution in Any Selected Time Interval at Monitoring Point 1

The spectral characteristics obtained from the Fourier analysis of the pressure signal can quantitatively verify the above oscillation characteristics. The following Fig.6a shows the existence of an oscillation frequency with a dimensionless frequency of about 5.2 (Frequency=1/t).

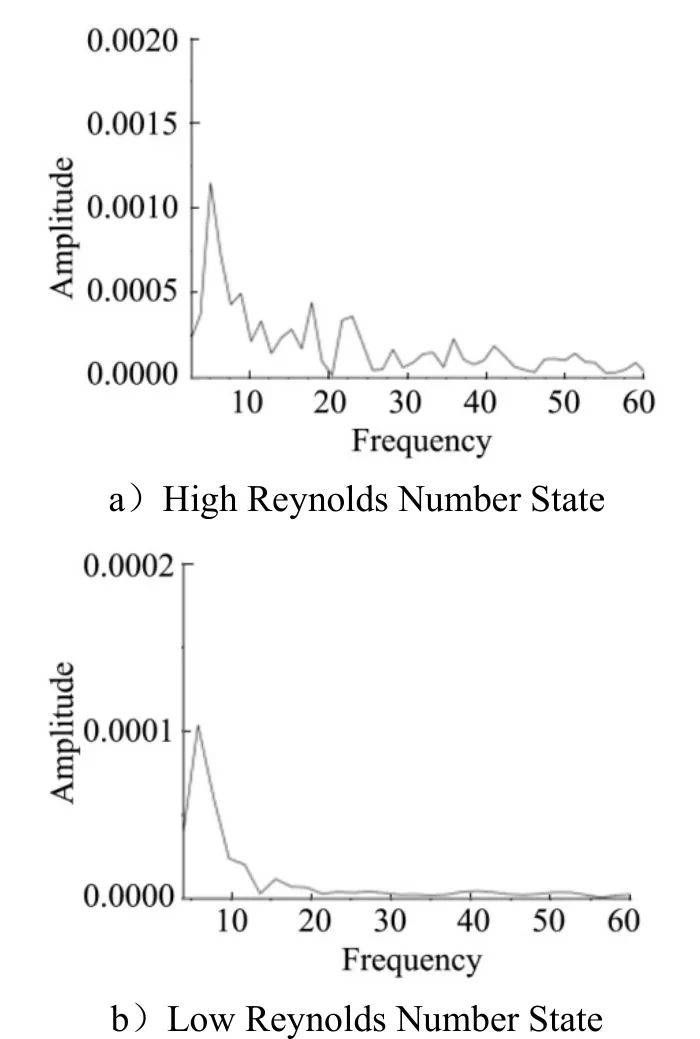
Fig.6 Spectral Characteristics based on the Pressure Signal at Monitoring Point 1

Fig.6b shows the spectral characteristics of the pressure signal at monitoring point 1 in Fig. 4b for the low Reynolds number condition. It can be seen that there is still an oscillation frequency with a dimensionless frequency of about 5.3. It indicates that the structural instability characteristics exist in the bottom flow at different Reynolds number states, and the structural instability mode of the bottom flow remains unchanged under the action of different external environments (disturbance conditions), which only causes a certain difference in the oscillation frequency.

2.1.2 Similarities and Differences in Flow Instability Characteristics of the Shoulder

Shoulder shear is a prevalent physical phenomenon in high-speed blunt body bypass flow, and its destabilization characteristics vary significantly at different Reynolds numbers. The locations of monitoring point 2 in Fig.4b were chosen near the respective shear initiation destabilization locations, and the pressure distribution at monitoring point 2 for the high Reynolds number condition with time is shown in Fig.7.

Fig.7 Pressure Distribution at Monitoring Point 2 for any Selected Time Interval

The Fourier analysis of this pressure signal is performed to obtain its spectral characteristics, and it can be seen from Fig. 8a that there is a topological oscillation frequency with a dimensionless frequency of about 5.2, which is the overall oscillation frequency of the shear layer affected by the bottom separation, and another dominant frequency of about 14, which is generated by the instability of the shear layer itself and corresponds to the fundamental frequency of the shear layer. The high frequency is less at this time, which also confirms that the shear layer is in the initial destabilization state.

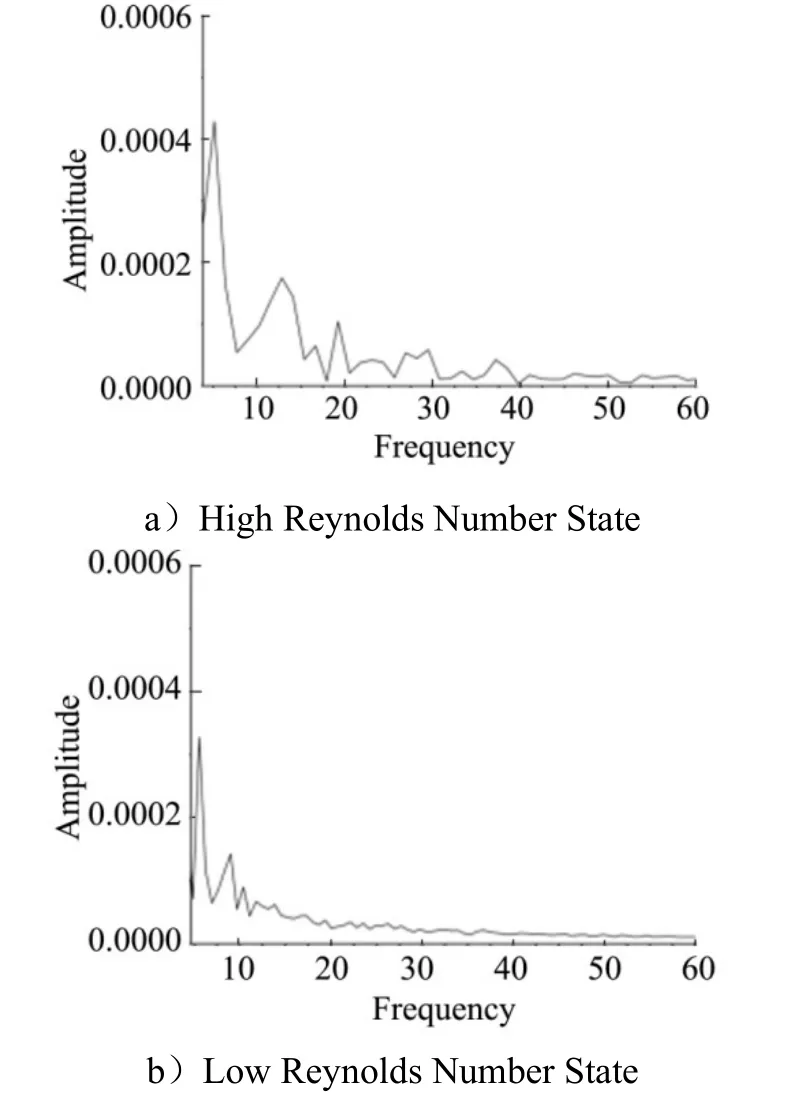
Fig.8 Spectral Characteristics based on the Pressure Signal of Monitoring Point 2

Fig.8b shows the spectral characteristics of the pressure signal at monitoring point 2 in the low Reynolds number condition. It can be seen that there is an overall oscillation frequency affected by the bottom separation and a shear layer initiation destabilization frequency, and the other high frequencies are not excited, so it can be assumed that the shear layer is just destabilized at this time. Since the position of monitoring point 2 in Fig.4b is farther back than that of monitoring point 2 in Fig.4a, the shoulder shear instability in the low Reynolds number condition is already very close to the tail mixing region.

In summary, from the analysis of the stability characteristics of the bottom flow region and the shoulder shear region under different Reynolds number states, it can be seen that both the bottom flow structure instability and the shoulder shear instability have their own characteristics in their respective dominant regions, and act as mutual perturbation sources to drive their respective instability histories, and the lower Reynolds number leads to delayed shear layer instability.

2.1.3 Similarities and Differences of Coupled Instability Characteristics in the Tailing Area

In the wake development area, it can be expected that the two destabilization modes will interact in a complex manner, resulting in coupled destabilization, leading to complex physical phenomena such as turning, turbulence, and Karman-like vortex streets in the wake area. The trailing development zone is selected as the pressure signal monitoring point (see Fig.4, monitoring point 3) to analyze its spectral characteristics.

Fig.9 show the spectral characteristics of the pressure signal at monitoring point 3 in the high and low Reynolds number condition. It can be seen that the similarity between the different Reynolds number states is the presence of the bottom structure instability frequency, and the difference is the shear instability and the broad spectrum characteristics after the action of shear instability and bottom structure instability. In the high Reynolds number state, more high frequency energy is excited.

The purpose of monitoring point 4 in Fig. 4 is to monitor the physical phenomenon of Karman-like vortex street, and the spectral characteristics of the pressure signal monitoring point in the wake region at high Reynolds number are shown in Fig.10.

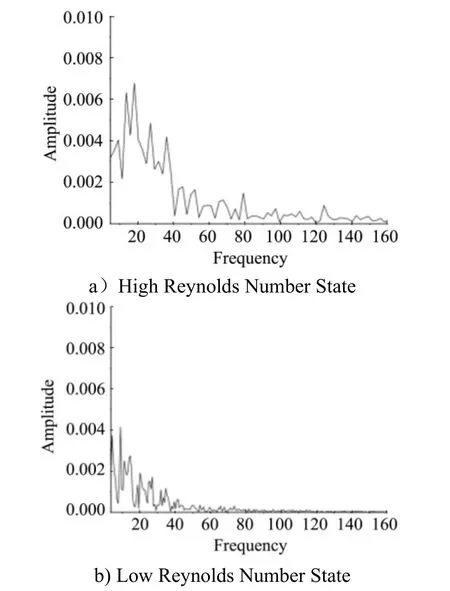
Fig.9 Spectral Characteristics of the Signal Monitoring Point 3

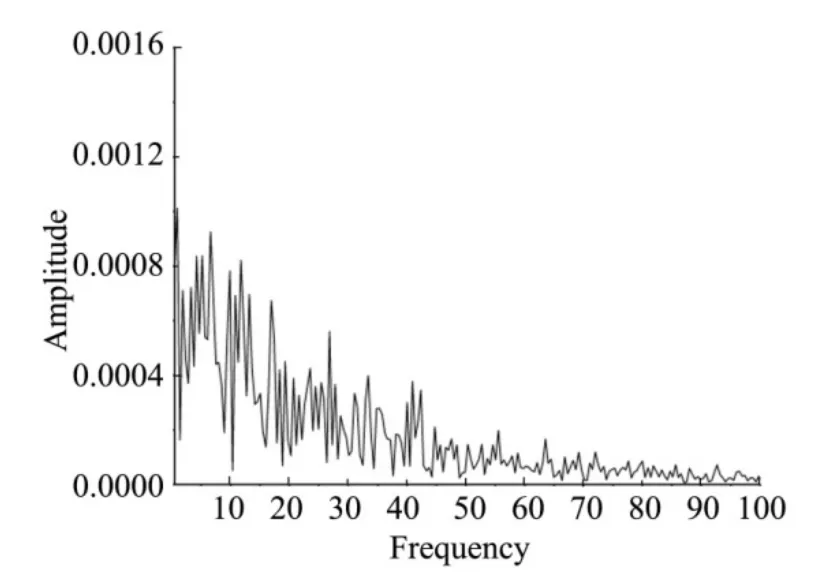
Fig. 10 Spectral Characteristics of the Signal at Monitoring Point 4 in the High Reynolds Number Condition

As can be seen in Fig.10, more high frequency energy is excited in the wake region, implying the presence of more small-scale vortices, i.e., turning and turbulent behavior. For a Karman vortex at high Reynolds number, the oscillation frequency equation isf=St∙(U∞/D) with a dimensionless parameterSt=0.27,U∞is the incoming velocity andDis the diameter of the winding object, which is estimated asf=0.27×(1.0/0.254)=1.06. This is close to the dominant dimensionless frequency of about 1.1 that appears in the spectral analysis.

2.2 Effect of Reynolds Number on Re-Entry Vehicle Winding

In summary, the bottom flow instability of high-speed re-entry vehicles at different Reynolds number states are both mainly dominated by the separation instability mode and the shear instability mode together. The coupling effect of the two instability modes will form a Karman-like vortex flow behavior in the far wake region.

The Reynolds number has the greatest influence on the shear-layer instability mode, and the size of the bottom separation region also has a significant influence on the wave system structure in the bottom flow region, such as the intensity and angle of the recompression wave, which also has a significant influence on the amplitude of the oscillation of the Karman-like vortex street. These effects need to be focused on in the study of shoulder heat flow, bottom drag, flight vibration, and wake effects of re-entry vehicles.

Although this paper has achieved some knowledge on the effect of Reynolds number on the re-entry vehicle winding flow, it should be noted that the implicit large vortex simulation method used in this paper does not include any artificial perturbation information, and for the Shenzhou-like return module shape, its precursor boundary layer attachment area is long, and the turning behavior may occur before the appearance of the shear layer, so it is necessary to consider the introduction of perturbation information in the precursor on the basis of this method, and the subsequent work will be This research work will be carried out in the future.

3 Conclusion

In this paper, the flow pattern and stability characteristics of the bottom of the Shenzhou-like return module shape under different Reynolds number conditions were carefully characterized by using large eddy simulation method. The similarities and differences of the bottom flow characteristics of the Shenzhou-like return module under different winding conditions are analyzed from various perspectives, such as shoulder shear instability, bottom separation instability, coupled instability in the tail track development area and far tail track area. The results show that the Shenzhou-like return module shape flow is basically laminar under low Reynolds number conditions, the shoulder shear layer is destabilized late, the bottom separation zone is larger, and the oscillation amplitude of the Karman-like vortex in thewake region is smaller. The low and high Reynolds number conditions have significant effects on the shoulder shear destabilization mode, and have less effect on the bottom flow structure destabilization mode. These research results will provide some basic theoretical support for the research of re-entry vehicle shape design, stability control and wake disturbance.