一类非齐次退化抛物方程的零可控性
杜润梅, 梅海婷, 陈博远
(长春工业大学 数学与统计学院,吉林 长春 130012)
偏微分方程一直是应用数学领域十分活跃的研究课题之一[1],抛物方程是偏微分方程中重要的一类。伴随科技的发展,抛物方程控制理论与其他学科联系越来越紧密。人们对非退化抛物方程的可控性问题进行了广泛研究[2-5],但是对退化抛物方程的研究较少[6-7]。文献[8]证明了如下退化抛物方程的零可控性:
ut-(xαux)x=fχω, (x,t)∈(0,1)×(0,T),
u(x,0)=u0(x),x∈(0,1),
其中,f∈L2((0,1)×(0,T)),u0∈L2(0,1),ω=(x0,x1)⊂⊂(0,1),χω是ω上的特征函数。
文中考虑如下方程的零可控性问题:
ut-(xαux)x=F+fχω,(x,t)∈(0,1)×(0,T),
(1)
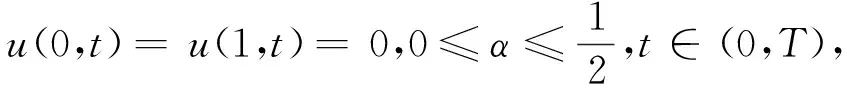
(2)
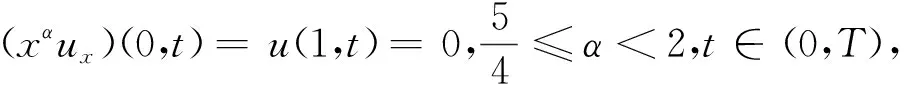
(3)
u(x,0)=u0(x),x∈(0,1),
(4)
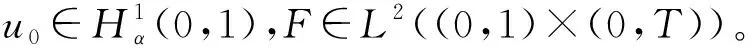
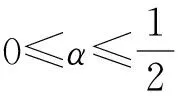
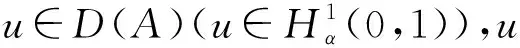
类似文献[8],可以证明问题(1)~问题(4)是适定的。
引理1对于任意u0∈L2(0,1), 问题(1)~问题(4)有惟一解
并且满足
其中,C是一个与α、u0、f和F无关的正常数。此外,如果u0∈D(A),
H1(0,T;L2(0,1)),
有


其中,C是一个与α、u0、f和F无关的正常数。
为了得到问题(1)~问题(4)的零可控性,需要考虑其对偶问题,
vt+(xαvx)x=0, (x,t)∈(0,1)×(0,T),
(5)
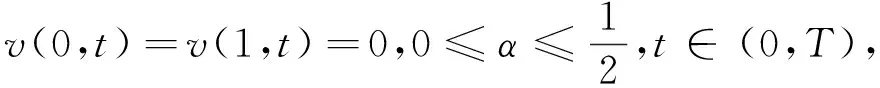
(6)
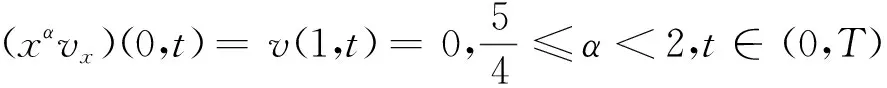
(7)
v(x,T)=vT(x),x∈(0,1),
(8)
其中,vT∈L2(0,1)。
由文献[8]可以得到如下定理。
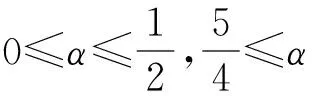
其中,
引理3(可观测性不等式)[9]设T>0,ω是(0,1)上非空子区间,则存在常数M2>0,问题(5)~问题(8)的解满足
由文献[2]可以得到如下命题。
命题1考虑最优控制问题
f∈L2((0,1)×(0,T)),
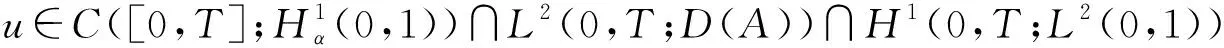
(vε)t+(xα(vε)x)x=0,(x,t)∈(0,1)×(0,T),
(9)
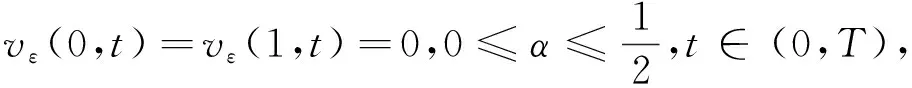
(10)
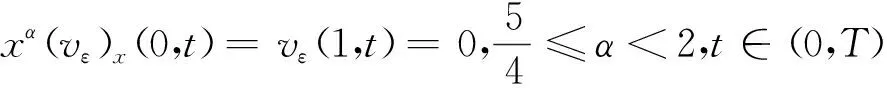
(11)
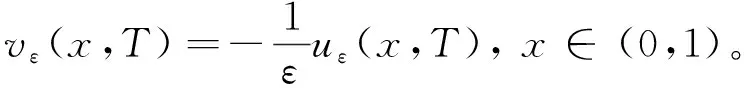
(12)
定理1(零可控性) 令F0∈L2((0,1)×(0,T))使得
几乎处处(x,t)∈(0,1)×(0,T),其中,R≥R0。则对任意u0∈D(A),存在f∈L2((0,1)×(0,T)),使得问题(1)~问题(4)的解u满足u(x,T)≡0,并且
‖u‖L2((0,1)×(0,T))≤
C(‖u0‖L2(0,1)+‖F0‖L2((0,1)×(0,T))),
式中:C——常数。
证明 由命题1,J(f)存在极小值点fε,相应于fε的问题(1)~问题(4)的解记为uε,则有
(uε)t-(xα(uε)x)x=F+fεχω,
(13)
因为u0∈D(A),由定理1(uε)t∈L2((0,1)×(0,T)),xα((uε)x)x∈L2((0,1)×(0,T))。在式(13)两边同时乘vε,其中,vε是问题(1)~问题(4)的解,并在(0,1)×(0,T)上积分,
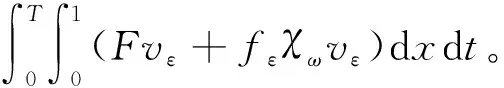
(14)
在式(9)两边同时乘uε,并在(0,1)×(0,T)上积分
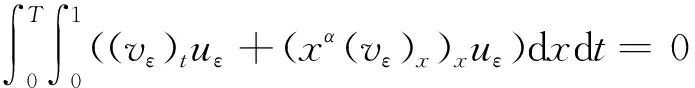
(15)
对式(15)分部积分得
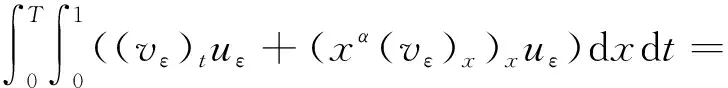
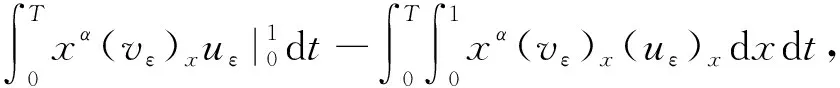
(16)

(17)
把式(16)和式(17)代入式(15),得
上式代入式(14),得
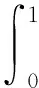
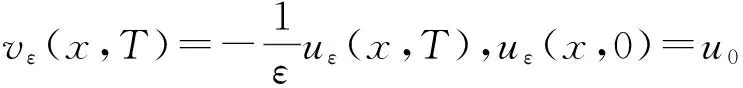
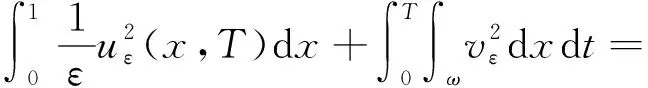
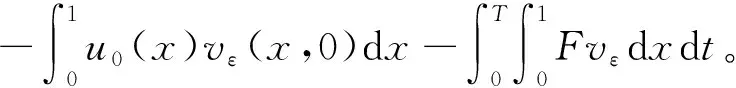
(18)
由引理2得

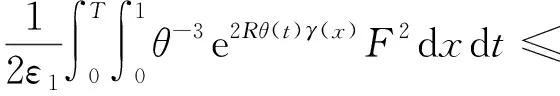
由引理3得,
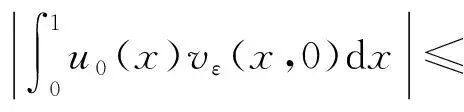
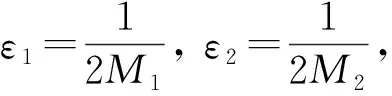

存在f∈L2((0,T)×ω),使得fε→f,在L2((0,T)×ω)中弱收敛,定义
由弱解定义,可证明u是相应于f*的问题(1)~问题(4)的解,由L2范数的弱下半连续性可知,
‖f*‖L2((0,1)×(0,T))≤
C(‖u0‖L2(0,1)+‖F0‖L2((0,1)×(0,T))),
且
定理证毕。

