基于非对称GARCH-MIDAS模型的原油价格波动预测

董小刚，费佳欣，秦喜文

(长春工业大学 数学与统计学院，吉林 长春 130012)

0 引 言

原油作为人类生产的必需品，学者们对其价格、波动等进行了研究。大多数文献利用原油价格的历史信息，基于GARCH类模型预测油价的条件波动[1]。Peny Sadorsky等[2]表明GARCH类模型比任何其他竞争模型产生更准确的预测。波动率测量和建模包含在GARCH框架中，鉴于超高频数据的广泛可用性，当前大多数做法是以已实现波动率的众多变体之一的形式直接测量波动率，然后建立预测模型。Nomikos Nikos K等[3]使用Mix-GARCH和MRS-GARCH模型预测1 d的原油价格波动。Sang Hoon Kang等[4]将ARFIMA模型与GARCH模型相结合，产生1、5、20 d的预测。但是这类预测涉及原油价格的历史数据分析，忽略了综合影响预测目标的各种外部因素。

原油价格受到一系列动态和多维因素的驱动，因此，在预测原油价格波动时，考虑原油价格的影响因素，需要构建一个合理的预测模型。为了提高预测精度，大多数研究人员在预测模型中引入了有效因素。考虑到预测因素的合理性，研究人员从多个角度使用不同的影响因素预测原油价格波动。一些研究依赖基本市场信息分析和预测原油价格波动。Stephane Dees等[5]将原油价格建模为原油库存和需求、石油输出国组织(OPEC)产量、生产者配额和产能的函数。周喜安等[6]分析了国际原油价格上涨原因，认为是需求增加、库存下降、OPEC保价等原因的共同作用。然而，考虑到原油价格波动受到金融资本、货币等因素的影响，研究人员开始基于原油市场金融化的信息来分析原油波动。韩冬炎[7]指出世界原油供求关系变化是最为重要的因素。Haugom E等[8]在预测模型中引入了商品市场指标，包括VIX指数、交易量和未平仓利率，有效预测原油波动。

Robert F Engle等[9]提出一种混合频率方法：GARCH-MIDAS模型。该模型具有两个乘性成分：短期成分服从GARCH(1,1)过程，可能被以相同频率观察到的其他变量所丰富;而长期成分是较低频率观察到的平滑滤波器。对于单变量GARCH-MIDAS模型的文献已经非常普遍。Luc Bauwens等[10]在多变量环境中构建了GARCH-MIDAS模型;Amendola A等[11]提出双非对称 GARCH-MIDAS模型，研究了波动率动力学中的非对称性;Engle R F[12]提出GARCH-X模型，此模型在短期组件中考虑了其他外生变量。

文中要解决特定的问题，即考虑非对称效应GARCH-MIDAS模型是否对原油价格波动存在不同的影响,以及能否更好地预测原油价格波动。为此，考虑两种非对称效应：

1)短期成分的非对称。将标准GARCH-MIDAS模型中短期成分服从GARCH(1,1)修改为TGARCH(1,1)。

2)长期成分的非对称。在两处地方进行了修改，即将原油价格波动因素的符号不对称性作为附加的解释因素，并赋予相应符号不同的权重函数。

此外，文中在GARCH-MIDAS的短期成分中考虑额外的波动决定因素——原油波动率指数(OVX)，观察在GARCH-MIDAS-X类模型中是否也存在非对称效应。

1 原油价格波动率预测的模型构建

1.1 GARCH-MIDAS模型

构建GARCH-MIDAS模型，并对原油价格波动建模，表示如下

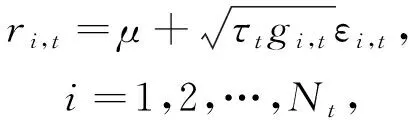
(1)

式中：ri,t——t月第i天时的对数收益率，是日度频率数据；

Nt——t月份的交易天数；

εi,t——扰动项，服从条件标准正态分布，即εi,tΨi-1,t～N(0,1)，Ψi-1,t表示在t月份第i-1天可获取的信息集。

显然，波动率由τt和gi,t两个成分组成,τt和gi,t分别为长期组成部分(每月频率)和短期组成部分(每日波动)。

gi,t服从GARCH(1,1)过程

(2)

本着MIDAS回归的精神，通过平滑已实现波动率来指定τt，

(3)

其中，K为低频变量的最大滞后阶数，φk(ω1,ω2)定义为MIDAS的权重方程，由Beta多项式进行计算，

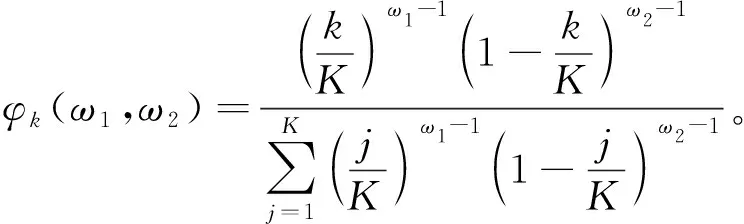
(4)

令ω2=1，使其权重函数为ω1的单调函数。式(1)～式(4)共同构建了GARCH-MIDAS模型。

1.2 非对称GARCH-MIDAS模型

将非对称效应纳入到GARCH-MIDAS模型，短期成分将标准GARCH过程修改为TGARCH过程，长期成分将解释变量的符号不对称性作为附加的解释变量。

1.2.1 短期成分的非对称

在标准GARCH-MIDAS模型中考虑短期成分的非对称效应，构建一个TGARCH-MIDAS模型，以包含非对称效应的短期影响，定义如下

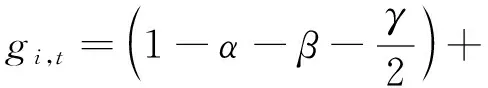
βgi-1,t，

(5)

其中α>0,β>0,α+β+γ/2<1且E(gi,t)=1，1{}为指示函数，即1{ri-1,t<0}=1时为负收益，1{ri-1,t<0}=0时为正收益。

1.2.2 长期成分的非对称

对长期成分的MIDAS回归考虑非对称效应，改进后的方程为

(6)

其中，m为截距，θ+和θ-反映了非对称效应，φk(ω)+和φk(ω)-为加权函数，文中使用Beta函数作为权重函数，即

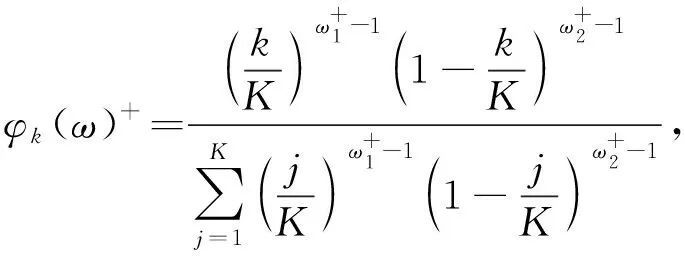
(7)

(8)

1.3 GARCH-MIDAS-X模型

将短期成分扩展到一些额外的波动决定因素，这些因素的频率应与对数收益率ri,t的频率相同，能够使我们跳出经典的GARCH-MIDAS框架，在式(2)和式(5)中包含“-X”部分，短期成分将分别修改为：

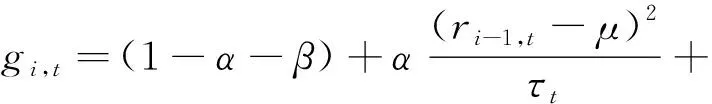
βgi-1,t+z·(Xi-1,t-E(Xi-1,t))，

(9)

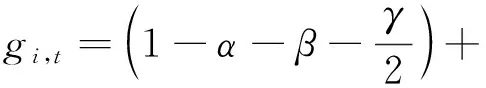
βgi-1,t+z·(Xi-1,t-E(Xi-1,t))。

(10)

E(Xi-1,t)表示该因素在t周期内到第i-1天的时间跨度内的均值，假设z≥0,Xi,t≥0，且Xi,t是平稳的，E(Xi,t)<∞，当短期成分是式(10)时，这样假设可以保证gi,t>0，且修改后的短期成分的无条件期望仍然为1。

文中模型共有8种，GARCH-MIDAS模型及其扩展模型的短期成分和长期成分公式见表1。

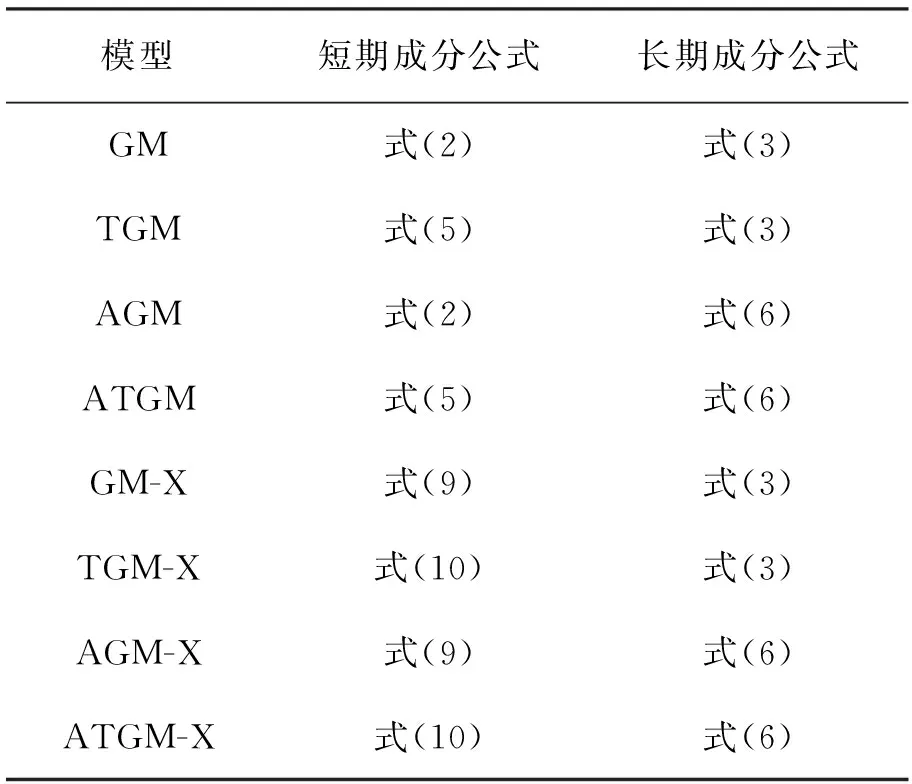
表1 GARCH-MIDAS模型及其扩展模型的结构

1.4 模型评价

通过模型置信集检验(MCS)比较了非对称GARCH-MIDAS模型和标准GARCH-MIDAS模型的性能，最后使用损失函数衡量不同模型的预测精度，文中选择以下两个损失函数作为预测误差标准：

(11)

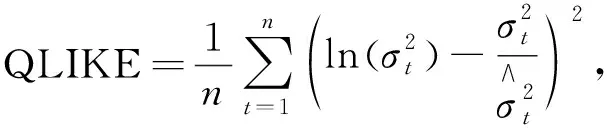
(12)

式中：n——波动率预测的总数量;

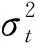
Yanran Ma等[13]指出损失函数无法提供有关模型之间的预测损失差异是否具有统计学意义的信息，因此，文中采用MCS检验。MCS检验的优点为不需要指定基准模型，在模型的整个集合中删除性能最差的模型，直到在α显著性水平上不再拒绝相同预测精度的零假设，生存下来的模型集为最优模型集。文中采用检验零假设的统计量为TSQ，

(13)

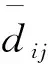
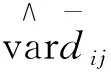
2 原油价格波动率预测的实证分析

2.1 数据

文中实证分析主要应用于代表国际原油价格水平的西得克萨斯轻质原油现货价格(WTI)，计算其对数收益率(ri,t)和已实现波动率(RV)；考虑的原油价格波动因素为代表原油供给的欧佩克原油产量(OPEC)和代表原油库存水平的美国原油商业库存(USI)，考虑的额外市场活动变量为代表未来30 d原油市场预期波动程度的原油波动率指数(OVX)，OVX由美国芝加哥期权交易所(CBOE)推出。

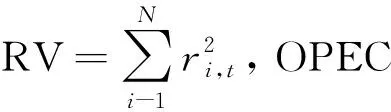
WTI对数收益率、WTI已实现波动率、OVX指数、OPEC原油产量以及美国原油商业库存的均值、偏差、偏度、峰度和数据频率见表2。

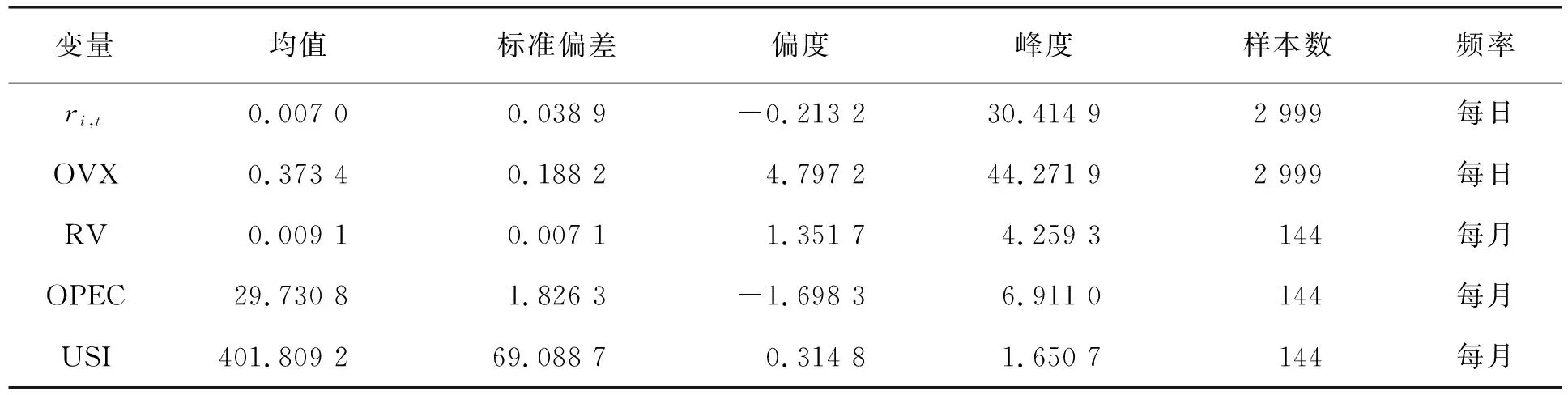
表2 描述性统计

WTI对数收益率和OPEC原油产量为左偏，其他变量均为右偏，并且除了美国原油商业库存的其余变量峰度值均大于3，说明变量存在尖峰厚尾的特征。

对各变量进行ARCH效应检验，结果见表3。

所有变量在滞后5、10、20 d的ARCH效应检验中具有1%的统计学显著性，即变量存在ARCH效应，因此使用GARCH类模型进行建模是适当的。

WTI对数收益和波动率的序列图如图1所示。

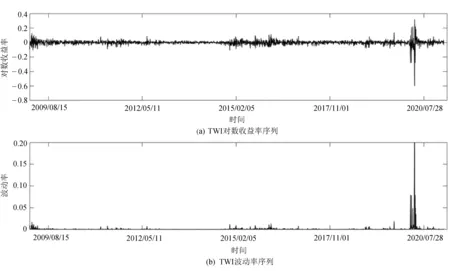
图1 TWI的对数收益和波动率

从图1可以看出，原油价格收益率的波动表现出聚集现象，与对原油的分析结果相符[14]。2020年出现样本期内的最大波动，反映出疫情对原油价格波动的重大影响。此外，2009年出现的波动较其他时期出现了小幅波动，说明金融危机时期对原油价格波动也产生了一定影响。

2.2 样本内估计结果

基于RV的不同模型参数估计值见表4。

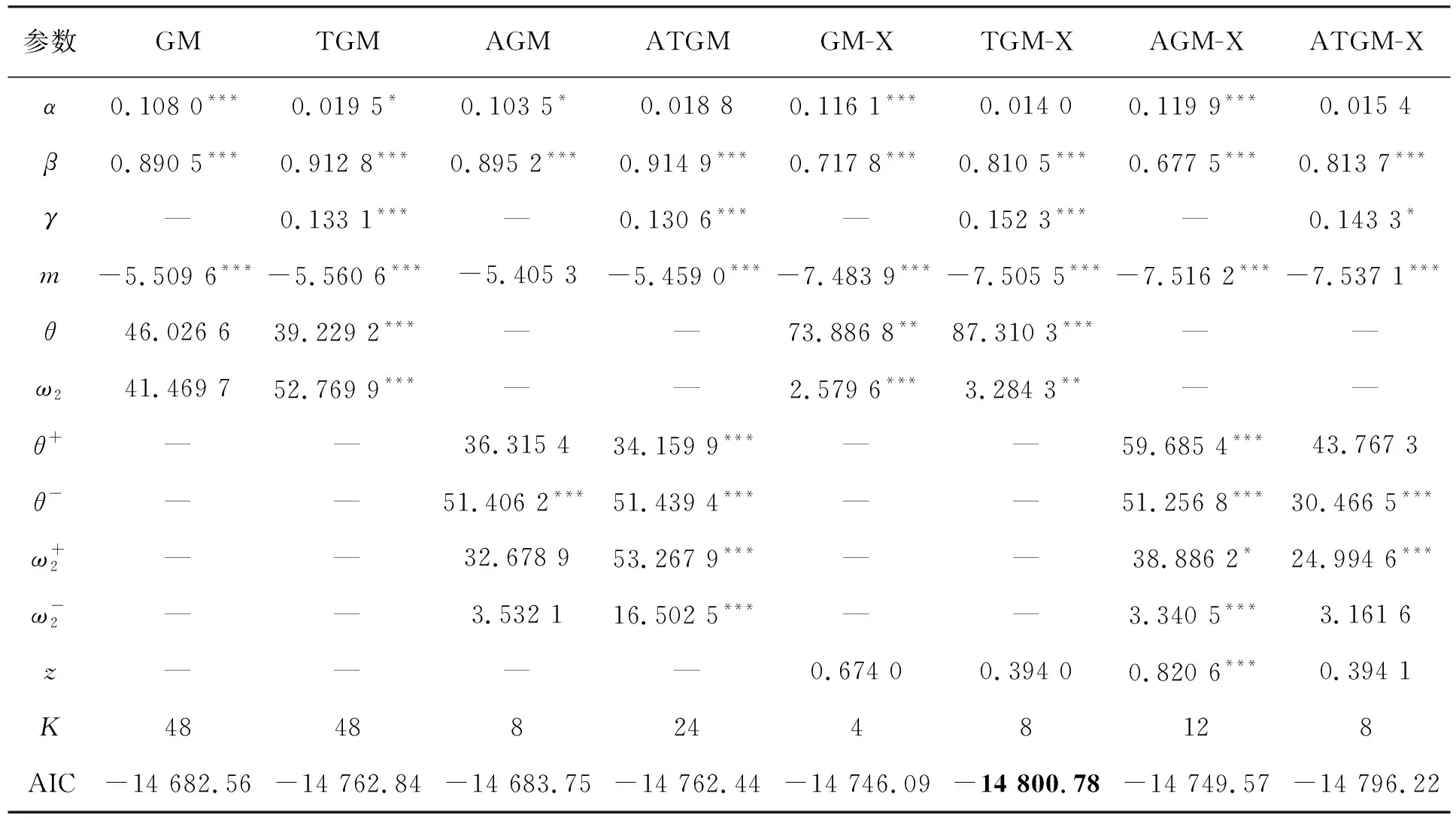
表4 基于RV的模型参数估计结果

其中α和β的总和接近于1，且β参数显著性都为1%，说明存在强烈的波动持久性。首先考虑短期成分的非对称性，短期波动的不对称参数γ对原油市场价格波动性具有显著影响，说明好信息和坏信息对原油波动的影响是不同的。此外，在长期成分的非对称性中，θ+和θ-的显著性不同，一般情况下，θ-的系数在1%水平下显著,但θ+不显著，表明坏信息会影响原油市场价格波动，而好消息对波动产生的影响较小。

另外，对各标准模型估计结果的绝对值进行比较，在大多数情况下，|θ-|>|θ+|，表明在相同程度上，坏信息与好信息相比，会导致更高的原油市场价格波动，说明波动与坏信息之间的联系要强于好信息。

诊断检验使用赤池信息准则(AIC)样本选择标准，相应结果见表4下部，用黑体给出了最佳拟合模型，显然，GARCH-MIDAS-X类模型都比GARCH-MIDAS类模型拟合得好，且考虑非对称效应的GARCH-MIDAS模型也都比标准GARCH-MIDAS模型拟合得更好。即修改后的模型在考虑短期成分和长期成分的非对称效应，并且将短期成分扩展到额外的波动决定因素时，可以更好地捕捉原油市场价格波动的特征。

2.3 样本外预测结果

通过样本外预测直接比较不同模型的性能，验证考虑非对称效应是否可以提高原油价格波动的预测能力。通过向前移动滚动窗口，生成了2021年1月1日至2021年2月28日样本期外的预测，共生成了38个日度预测。文中采用显著性水平为α=0.25的模型置信集检验来选择最优预测模型。

MSE和QLIKE的平均值见表5。

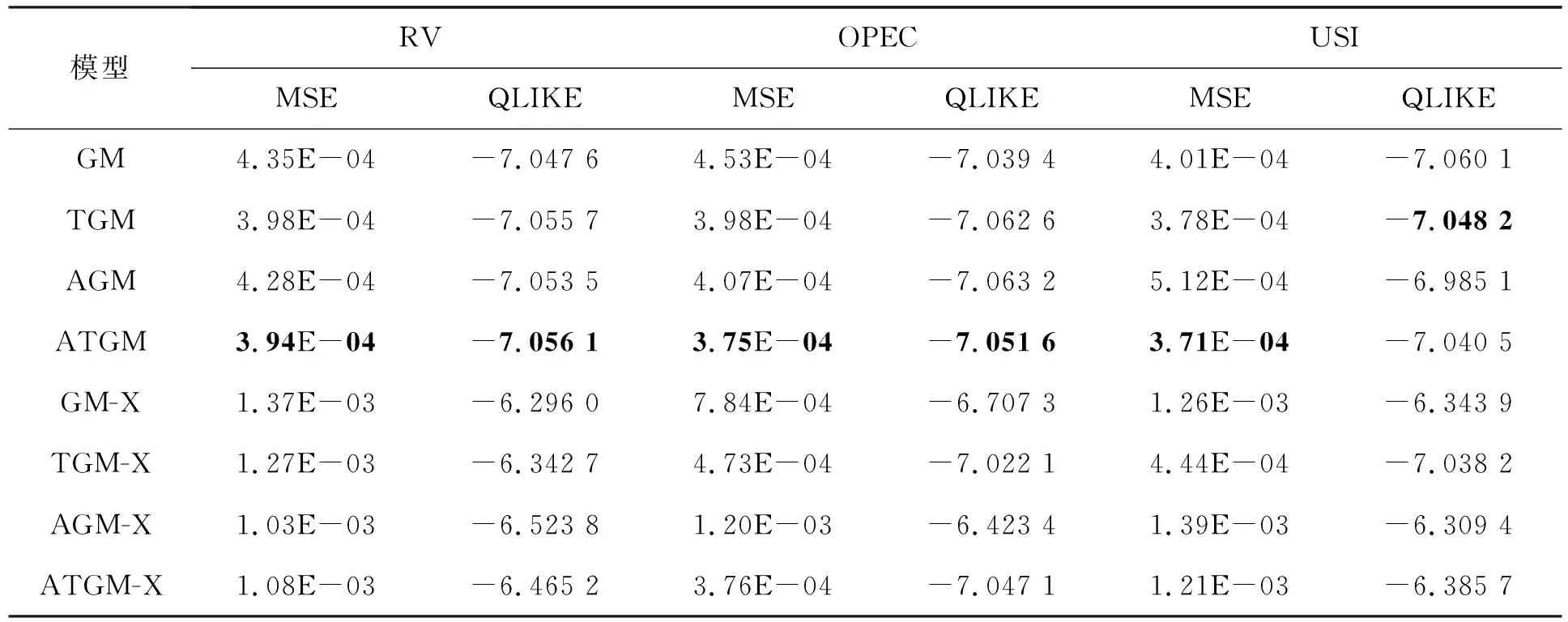
表5 样本外预测的平均MSE和QLIKE

确定了在显著性水平上通过MCS检验的最佳模型。结果显示，最优模型一般为ATGM。在GM类模型中最低的MSE和QLIKE都来自考虑非对称效应的模型，同样，在考虑额外波动因素OVX的GM-X类模型中也是如此。可以得到考虑非对称效应的GARCH-MIDAS比标准GARCH-MIDAS模型会产生更高预测性能的结论，这一结论表明,包括短期和长期成分的非对称效应可以有助于预测原油市场价格波动。此外，只考虑短期成分非对称效应模型的MSE都小于只考虑长期成分非对称效应模型的MSE，说明短期不对称性比长期不对称性更能提高波动率模型的预测能力。

3 结 语

通过考虑短期成分和长期成分的非对称效应，并将短期成分扩展到一些额外的波动决定因素，即考虑非对称效应的GARCH-MIDAS与GARCH-MIDAS-X共8个模型，分别用于建模和预测，预测了国际原油WTI价格的波动性，研究考虑非对称效应的模型是否可以达到更高的预测准确性。通过实证研究得到了几个重要的发现。首先，样本内估计结果表明，在GARCH-MIDAS模型中，非对称效应对原油价格波动存在显著影响，且好消息和坏消息对WTI波动性影响是不同的，通常情况下，坏信息与波动之间的关联要强于好信息。其次，在样本外预测性能方面，MCS检验结果表明，非对称效应GARCH-MIDAS模型优于标准GARCH-MIDAS模型，在预测波动率模型方面具有优越的性能，在GARCH-MIDAS-X类模型中也是如此。并且发现对于波动率模型预测能力的提高，更多的应该归因于短期成分的非对称效应。