有序贝叶斯网络在肥胖数据中的应用
陈芳芳,徐平峰
(长春工业大学 数学与统计学院,吉林 长春 130012)
0 引 言
自1980年以来,全球肥胖人口数量剧增,且因肥胖患病和死亡人数也在攀升[1]。胖瘦程度通常用身体质量指数(BMI)来衡量。2019年BMI偏高导致全球500万人死亡,主要死亡原因是由肥胖引起的心血管疾病和Ⅱ型糖尿病,另外,高BMI也会增加患癌症的风险。文中目的是寻找肥胖的影响因素,以及如何在这些因素下对一个人是否肥胖进行预测。肥胖等级是有序变量,各等级之间存在自然顺序,对有序变量建模不能直接使用决策树、随机森林等机器学习算法,这样做会损失有序信息,正确的做法是建立合适的有序分类器。
已经有学者提出一些算法专门用来解决有序分类问题,如有序logistic回归[2]、有序支持向量机[3]、有序神经网络[4]等。这些有序算法的目标都是得到准确率更高的分类器,但是影响决策的主要特征是哪些,特征之间是否存在依赖关系却没有探讨。针对肥胖问题,文中目的不仅能正确对肥胖等级进行预测,还要寻找影响肥胖的因素及各因素之间的关系。
针对已有分类器无法同时解决有序分类问题和不善于知识表达的缺点,Halbersberg D等[5]提出一种在给定初始网络的情况下,利用有序信息测度构建贝叶斯网络分类器的算法。有序信息测度能反映误分类的严重性,所得贝叶斯网能反映变量之间的依赖关系。但是Halbersberg方法[5]直接用朴素贝叶斯网(Naive Bayesian, NB)或者空的网络(Empty Network, EN)作为初始网络,而不同初始网络的选择可能会对分类器的性能产生影响,因此,文中用Kuschner K W等[6]的方法生成“平均”网络(Average Network, AN)作为初始网络,然后结合Halbersberg方法得到分类器。肥胖数据结果显示,新方法准确率显著提高,并且优于其他有序分类算法。从得到的贝叶斯网络发现,饮食习惯是影响肥胖的主要因素,此外,日常乘坐的交通工具类型也会对肥胖等级产生影响。
1 预备知识
1.1 贝叶斯网络分类器
贝叶斯网络分类器(Bayesian Network Classifier, BNC)是用来预测离散类别变量C的贝叶斯网络。对于一个分类问题(X,C),X=(V1,V2,…,Vm)表示观测特征,C表示类别标签,对应的贝叶斯网络结构用B=〈ζ,Θ〉表示,ζ是有向无环图,每个节点代表(X,C)中的一个变量,Θ表示量化该网络的一组参数。给定m个特征的观测值x=(v1,v2,…,vm),其中vi为x在第i个属性Vi上的观测值,则BNC为x分配最可能的类别c*,c*对应C中的某一个取值,即
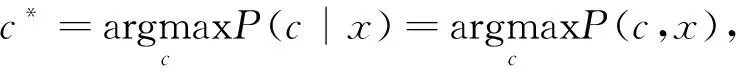
(1)
其中,P(c,x)可以根据贝叶斯网络的结构B=〈ζ,Θ〉分解得到,即
1.2 学习贝叶斯网络分类器
贝叶斯网络分类器的学习包括结构学习和参数学习两部分。结构学习通常是用搜索和评分的方法,如徐平峰等[7]提出的基于自助法(Bootstrap)的高斯贝叶斯网的结构学习算法BPKL。搜索和评分方法的基本思想是选择一个评分函数,该评分函数能测量结构对数据的契合度,然后基于评分函数寻找结构最优的贝叶斯网。但是从所有可能的结构中寻找最优网络是一个NP问题。能在有限时间内得到近似解有两种方法:
1)贪心法即贪婪搜索,从某个网络出发,通过对该网络加边、减边或改变边的方向(不形成闭环的情况下),寻找使评分函数最优的结构;
2)通过对网络结构施加约束来缩小搜索空间。
参数学习比较容易,就是在得到网络结构后,通过对训练样本计数得到每个节点的条件概率表。
1.3 评估指标
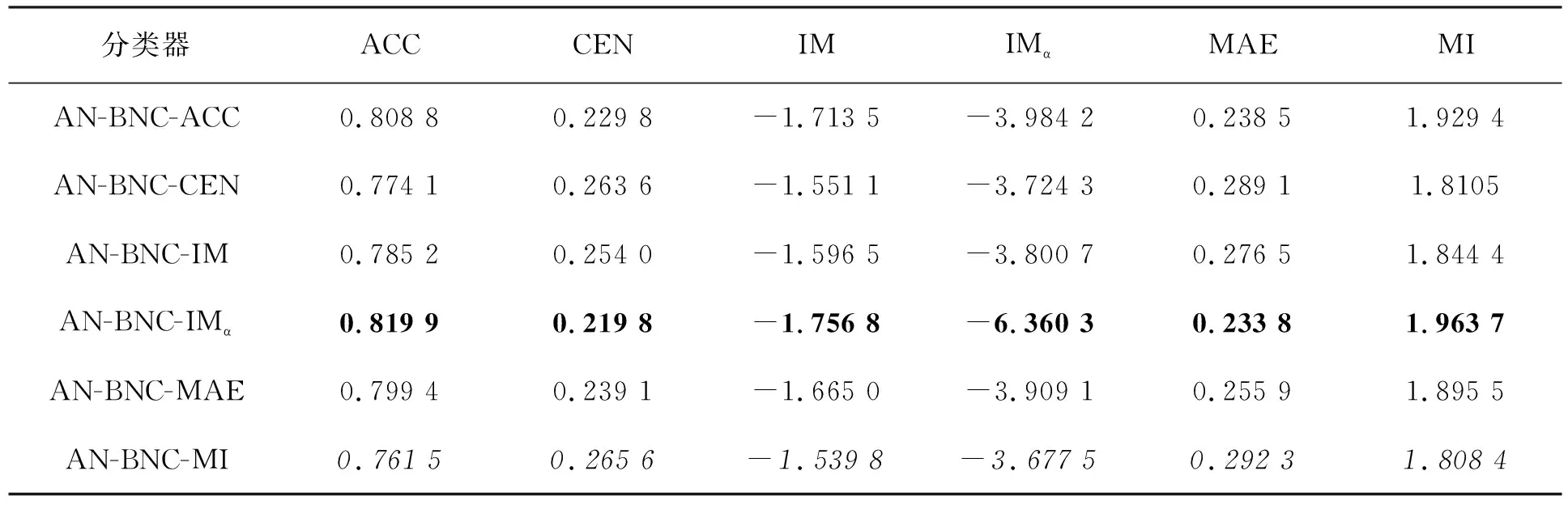
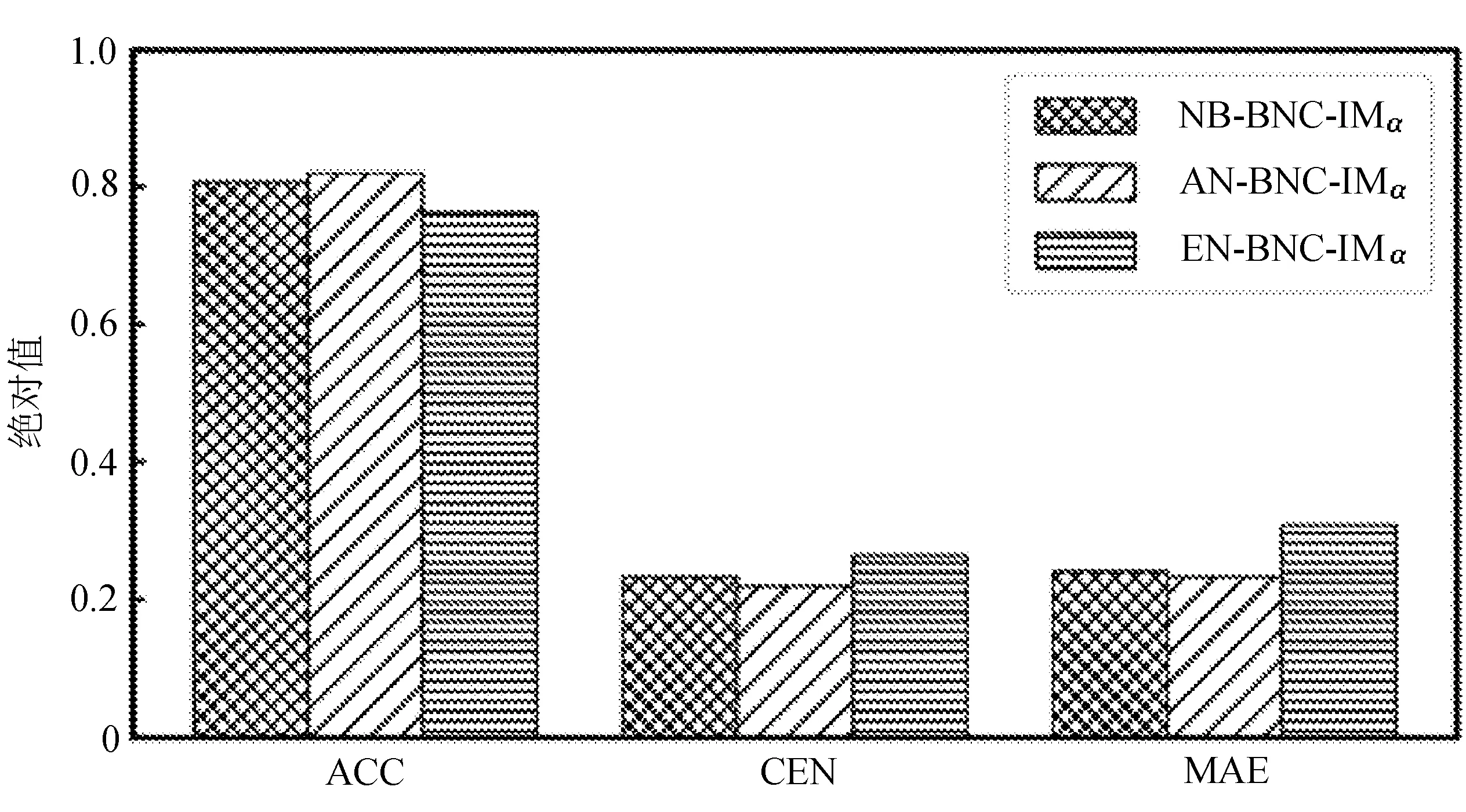
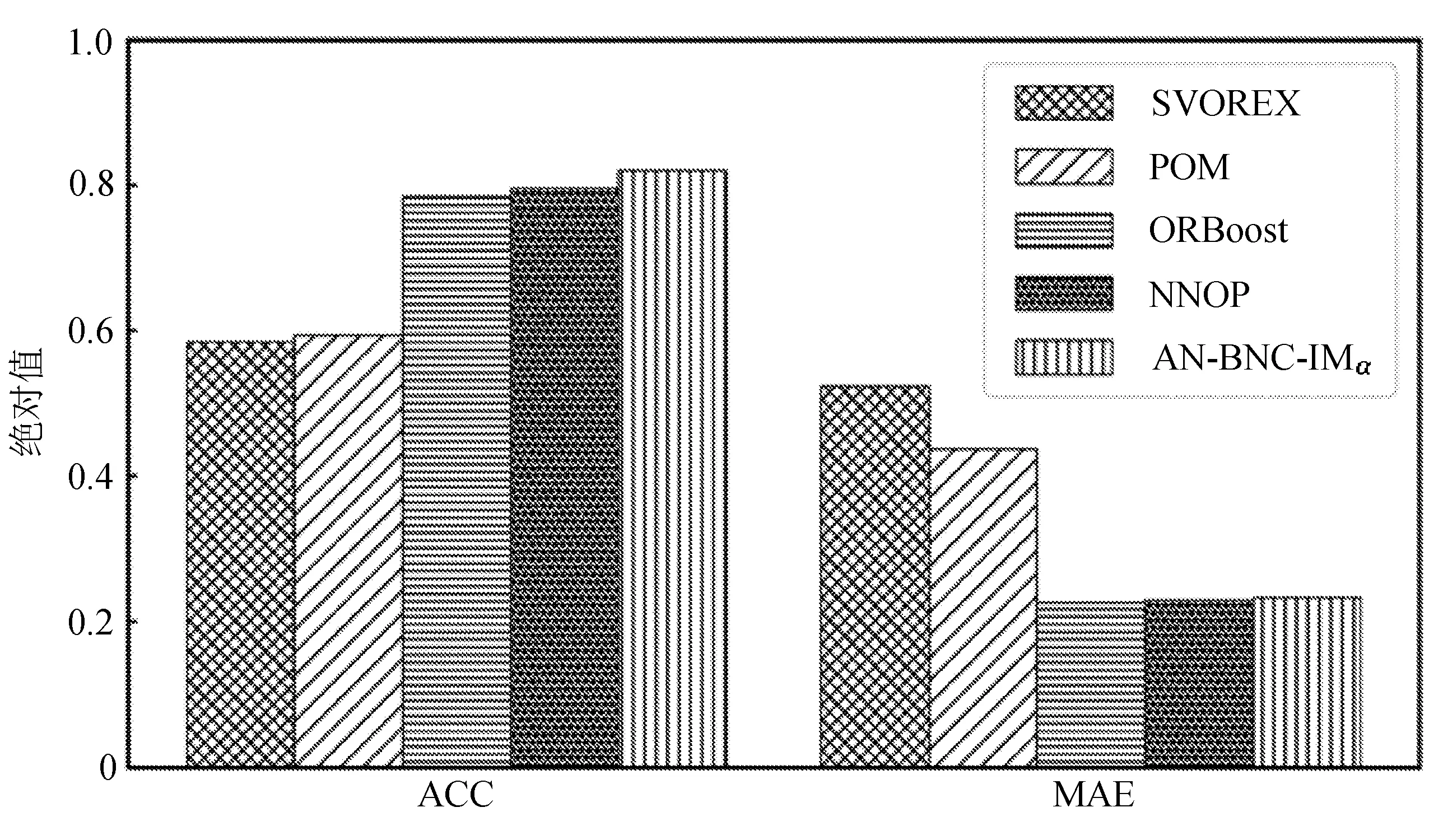
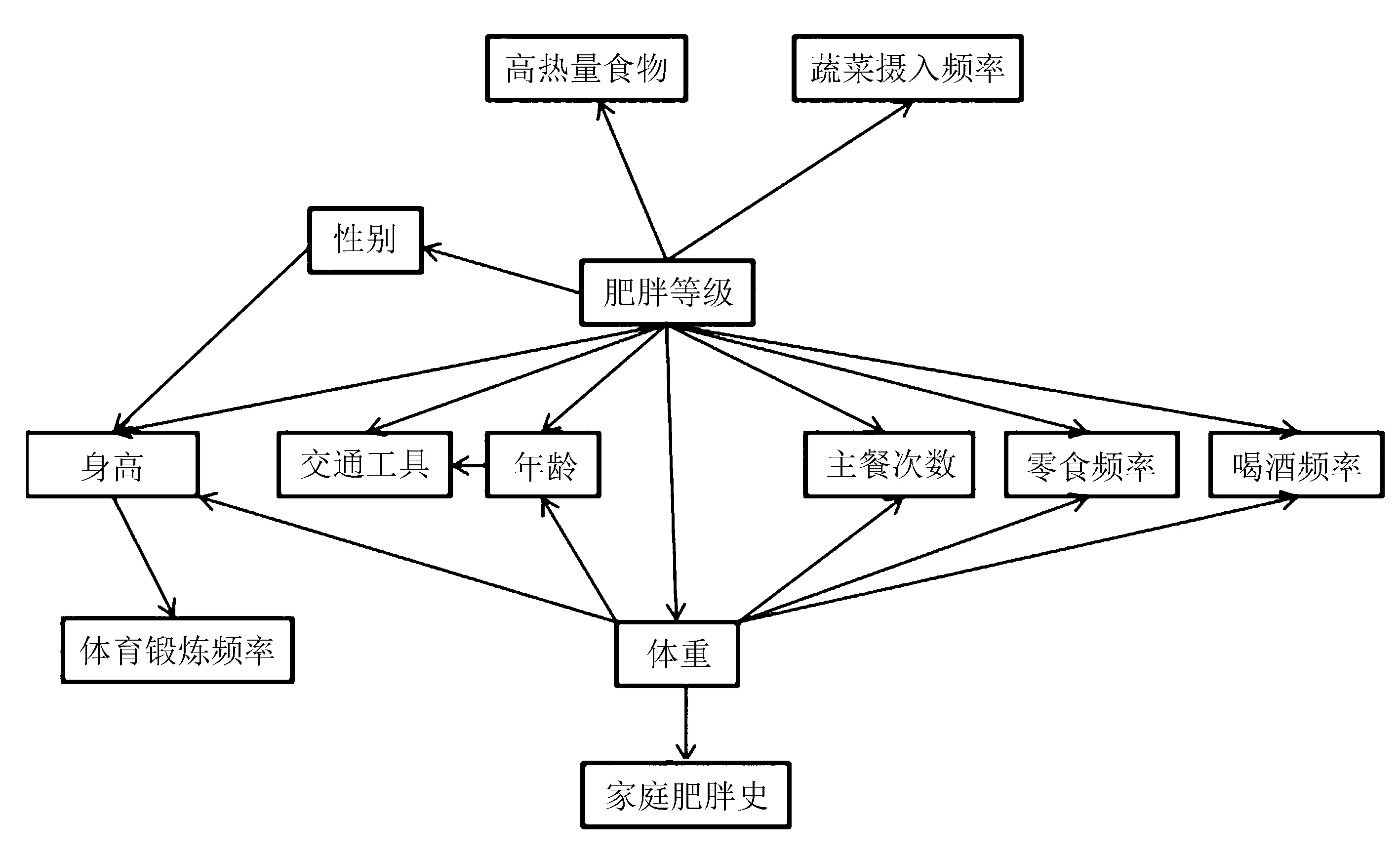
为比较不同分类器的好坏,需要进行性能评估。混淆矩阵是常用的记录分类器性能的矩阵,包含预测值和真实值的信息。假设某个数据集的样本量为N,可以分为k(k≥2)个类别,且类别之间是有序的,即d1 表1 混淆矩阵 令x表示预测类别,y表示真实类别。Cij(i,j∈[1,k])是混淆矩阵中位于第i行第j列的元素,表示真实类别为i而预测类别为j的样本量,显然 则被预测为第j类的样本频率为 (2) 样本属于第i类的频率为 (3) 真实属于第i类而被分到第j类的样本频率为 (4) 基于以上混淆矩阵可以定义一系列用来衡量分类器性能的评估指标,文中选取了6种评估指标。互信息(MI) 测量的是x和y的联合概率分布P(x,y)和边缘概率分布乘积P(x)P(y)的相似程度,离散变量的互信息定义为 它可以度量变量之间关系的强弱,取值越大越好。由混淆矩阵可以得到互信息的估计为 (5) 平均绝对误差(MAE)是预测标签x和真实标签y之间的平均偏差,是所有可能误差的总和,取值越小越好。由混淆矩阵可以得到 (6) 混淆熵(CEN)是Wei J M等[8]提出的一种新的评估指标。对于一个分类问题,某个标签i错误分类信息既包括属于第i类而被错误分到其他标签的样本信息,也包括其他标签样本被错误分到第i类的信息。混淆熵就是利用所有类的这种错误分类的分布信息来度量分类器性能,具体算法参见文献[8]。 信息测度(IM)由Halbersberg D等[5]提出,它能同时最大化分类精度和信息,也能通过错误严重性来体现类别之间固有的顺序,估计值为 IM=-MI(x,y)+ES(x,y)= (7) IMα= (8) 也可以表示为 IMα=IM-log(α)ACC, 其中,ACC为准确率,α在准确率ACC和互信息MI之间做权衡。当α=1时,IMα相当于IM,二者均越小越好。 建立分类器时需确定使用哪个度量来训练分类器,选择的度量方式可以和评估分类器的度量一致,如Kelner R等[9]既用准确率ACC学习分类器,也用准确率评估分类器;也可以不一致,如随机森林可以用信息增益进行训练,用准确率进行评估。文中应用贪心法选择相同的衡量指标对分类器进行学习和评估,这些指标来源于文中1.3。 Halbersberg D等[5]用IMα作为评分函数搜索最优贝叶斯网络。IMα可以用ES(x,y)来衡量有序分类中错误分类的严重性,能有效处理有序分类问题。该算法首先给出一个初始网络和α,然后用贪心法搜索使IMα得分最低的网络。但Halbersberg D[5]直接给定NB或者EN作为初始网络,而不同的初始网络得到的分类器不同,性能也不同。因此,希望通过某种方法寻找初始网络,利用该初始网络能提高最终分类器的性能。 Kuschner K W等[6]在建立贝叶斯网分类器时,将类别变量放在根节点处,根据互信息和条件互信息建立类别变量的马尔可夫毯(某节点的马尔可夫毯由该节点的父节点、子节点和子节点的其他父节点构成),同时也关注类别变量的子节点和其他变量的依赖关系。由于类别变量没有父节点,该方法简化了寻找贝叶斯网的过程,故用Kuschner方法[6]建立初始网络,然后结合Halbersberg方法[5]构建最终的贝叶斯网络形成算法1,见表2。 表2 算法1 文中将用X作为初始网络,Y作为评分函数,得到的BNC记作X-BNC-Y,其中X∈{NB,EN,AN},Y∈{ACC,CEN,IM,IMα,MAE,MI}。 文中选取来自Kaggle网站中的obesity数据集进行分析,该数据集包括17个特征共2 111个样本。类别变量分为体重偏轻、正常体重、Ⅰ级超重、Ⅱ级超重、Ⅰ级肥胖、Ⅱ级肥胖和Ⅲ级肥胖7个等级。除类别变量外,其余特征可分为3个方面: 1)与饮食习惯相关的特征。包括经常使用高热量食物、蔬菜摄入频率、正餐次数、零食频率、每日饮水量和饮酒量。 2)与身体状况相关的特征。包括卡路里消耗监测、体育锻炼频率、使用科技设备时间、使用的交通工具。 3)其他特征。包括性别、年龄、身高、体重、家庭肥胖史、是否抽烟,其中年龄、身高、体重是连续变量,将其进行离散化。 将1.3中的6种评估指标分别作为评分函数用算法1得到各自的BNC,对每个分类器在测试集上得到的混淆矩阵计算6种评估指标,所得结果见表3。 表3 相同初始网络不同评分函数所得分类器的结果比较 用NB和EN作为初始网络分别得到NB-BNC-IMα和EN-BNC-IMα,与AN-BNC-IMα进行比较,如图1所示。 (a) ACC、CEN、MAE (b) MI和取绝对值之后的IM和IMα 从图1可知,AN-BNC-IMα在6种评价指标中的表现一致优于另外两种分类器,说明AN-BNC-IMα较Halbersberg原始方法性能好。 将AN-BNC-IMα与其他有序分类算法进行比较,选择的比较算法有POM[2]、SVOREX[3]、NNOP[4]、ORBoost[10],这些方法都是传统分类器用于解决有序分类问题的变体,可以用ORCA(Ordinal Regression and Classification Algorithms)[11]来实现。ORCA是一个Matlab框架,它实现并集成了不同的有序分类算法,且有专门设计的评估指标,可以衡量分类器的性能。比较的评估指标是ACC和MAE,结果如图2所示。 图2 AN-BNC-IMα和其它有序分类器的比较 从图2可知,AN-BNC-IMα的准确率最高,NNOP次之,准确率相差2%;ORBoost的MAE最低,但是NNOP和AN-BNC-IMα的MAE也只有0.23,和ORBoost相差不到0.01。说明ORBoost、NNOP和AN-BNC-IMα3个分类器的性能相近,但是由于ORBoost、NNOP只给出分类结果,无法说明哪些特征对目标变量有直接影响,而贝叶斯网络可以直观地显示出变量之间的依赖关系,更有利于结果的解释,所以认为AN-BNC-IMα是最理想的分类器。 算法1得到的贝叶斯网络如图3所示。 图3 贝叶斯网络 从图3可以看出,影响肥胖程度的主要因素除年龄、性别、身高等基本情况外,主要与饮食习惯相关的属性,即高热量食物、蔬菜摄入频率、主餐次数、零食频率有关,另外还和交通工具有关。 对交通工具这一特征进行分析发现,使用摩托车、自行车和步行的样本占比极少,只占总样本量的3.5%,故只分析乘坐汽车和公共交通的人群。使用公共交通和汽车的人群在各肥胖等级中的占比如图4所示。 图4 使用公共交通和汽车的人群在各肥胖等级中的占比 从图4可以看出,乘坐公共交通的人群中体重偏轻、正常或属于Ⅲ级肥胖的比例显著大于在乘坐汽车的人群中同等级的占比;乘坐汽车的人群肥胖等级波动很大,Ⅲ级肥胖人数占比最少,Ⅱ级超重、Ⅰ级肥胖、Ⅱ级肥胖的比例较高,并且显著大于公共交通中同等级所占的比例。这说明和乘坐汽车的人群相比,乘坐公共交通工具的人群不容易肥胖,但是Ⅲ级肥胖除外。 采用Kuschner K W等[6]的AN方法建立初始网络,然后结合Halbersberg方法构建有序贝叶斯网络分类器,弥补了Halbersberg方法随机选择初始网络的不足。文中方法在肥胖数据上的结果显示,和使用朴素贝叶斯网(NB)或者空的网络(EN)作为初始网络相比,用AN作为初始网络所得分类器的性能在6种评估指标中一致最优,说明文中方法较Halbersberg方法效果提升明显。另外和其他有序分类器比较发现,在准确率和平均绝对误差上,文中方法显著优于SVOREX、POM,并且和NNOP、ORBoost的性能相当。而且可以通过贝叶斯网直观得出各变量之间的依赖关系,找到影响目标变量的直接因素,有助于结果解释。从得到的贝叶斯网络发现,影响肥胖的因素除了和饮食习惯相关的属性外,还与日常使用的交通工具有关。
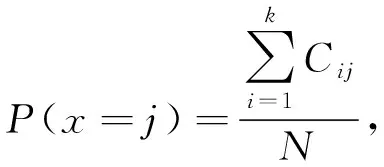
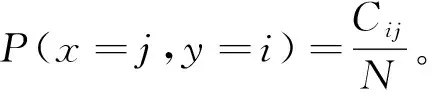
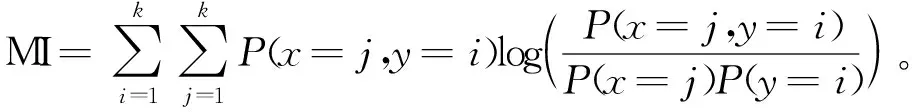
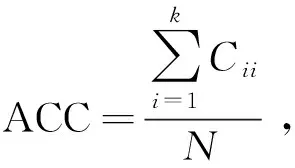
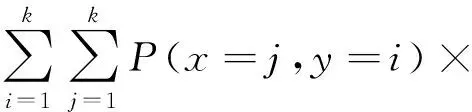
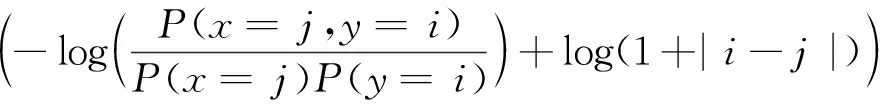
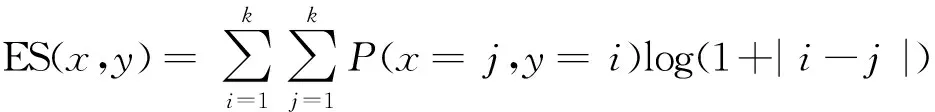
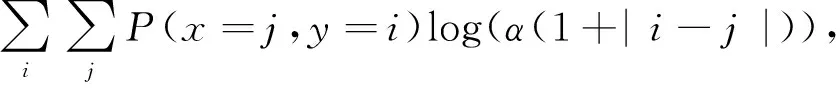
2 改进算法

3 实证分析
3.1 数据描述
3.2 算法应用及比较
3.3 影响因素分析

4 结 语

