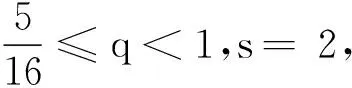锥b-度量空间中相容映像的不动点定理*

彭 荣，柴富杰

(1.广东培正学院数据科学与计算机学院，广东 广州 510830；2.广东金融学院金融数学与统计学院，广东 广州 510521)

不动点定理是泛函分析研究的重要内容.近年来，有学者对不动点所在的空间和压缩条件进行了各种形式的推广，获得了许多不同形式的不动点定理.Czerwik等[1]提出了b-度量空间的概念，证明了b-度量空间压缩映像原理；Huang等[2]通过引入锥度量空间，获得了锥度量空间中的不动点定理.此后，b-度量空间和锥度量空间中的不动点问题得到广泛关注[3-8].2011年，Hussain等[9]给出了锥b-度量空间的概念，推广和统一了b-度量空间和锥度量空间，证明了锥b-度量空间中的KKM压缩不动点定理.最近，Hussain等[9-15]将公共不动点问题的研究拓展到锥b-度量空间中.受此启发，笔者拟在锥b-度量空间框架下，研究一类广义压缩条件下2个相容映像对的公共不动点的存在性问题.

1 预备知识

定义1[2]设E为实Banach空间，θ表示E中的零元，称P是E中一个锥，如果P是E中的非空闭子集且满足如下条件：

(ⅰ)P≠{θ}；

(ⅱ)对于∀a,b∈R，a≥0，b≥0和∀x,y∈P，都有ax+by∈P；

(ⅲ)若x∈P且-x∈P，则x=θ.

设x,y∈E，若x⪯y⟺y-x∈P，xy⟺x⪯y且x≠y，x≪y⟺y-x∈intP(intP表示P的内部)，则称“⪯”和“≪”为E中偏序.在锥P中，若对于∀x⪯y存在常数N，使得‖x‖≤N‖y‖，则称P为正规锥，其中最小常数N称为正规常数.

定义2[9]设X为一个非空集合，E是实Banach空间，称d为X上的一个锥b-度量，s为度量系数，(X,d)为锥b-度量空间，如果映像d∶X×X→E满足：

(ⅰ)对于∀x,y∈X，有θ⪯d(x,y)且d(x,y)=θ⟺x=y；

(ⅱ)对于∀x,y∈X，有d(x,y)=d(y,x)；

(ⅲ)对于∀x,y,z∈X，有d(x,y)⪯s(d(x,z)+d(z,y)).

定义4[9]设(X,d)是锥b-度量空间，序列{xn}⊂X.对于∀c≫θ，存在n0∈N，当m,n>n0时，d(xm,xn)≪c，则称{xn}为Cauchy列.

引理1[9]设E是实Banach空间，P是E上的一个锥，则有：

(ⅰ)若{xn}为E中的序列，且θ⪯xn→θ，则对于∀c∈intP，存在n0∈N，当n>n0时，xn≪c；

(ⅱ)对于∀a,b,c∈E，若a⪯b且b≪c，则a≪c.

定义5[9]设(X,d)是锥b-度量空间，若X中的任意Cauchy序列{xn}都收敛于X中，则称(X,d)是完备锥b-度量空间.

定理1设(X,d)为锥b-度量空间，s≥1，序列{xn}和{yn}分别收敛于x，y，则有

证明因(X,d)为锥b-度量空间，故由定义2中条件(ⅲ)可得

d(x,y)⪯sd(x,xn)+s2d(xn,yn)+s2d(yn,y)，

(1)

d(xn,yn)⪯sd(xn,x)+s2d(x,y)+s2d(yn,y).

(2)

对(1)式下确界和(2)式上确界分别取极限，可得

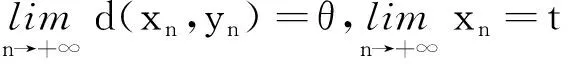
d(yn,t)⪯s(d(xn,yn)+d(xn,t))，

(3)

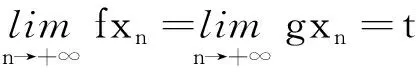
注1交换映像一定是相容的，但是相容映像不一定可交换.

2 主要结果

定理3设(X,d)是一个完备的锥b-度量空间，度量系数s≥1，f,g,S,T∶X→X是X上的自映像，对于∀x,y∈X，均有

(4)

其中q∈[0,1)，fX⊆TX，gX⊆SX，{f,S}和{g,T}为相容映像对且S，T连续，则f,g,S,T在X中存在唯一公共不动点.

证明任取x0∈X，由fX⊆TX可知存在x1∈X，使得Tx1=fx0，又由gX⊆SX可知存在x2∈X，使得Sx2=gx1，同理有Tx3=fx2，Sx4=gx3.依此类推，存在{x2n+1}，{x2n+2}⊆X，使得y2n=fx2n=Tx2n+1，y2n+1=gx2n+1=Sx2n+2.

(1)证明序列{d(yn+1,yn)}单调减且收敛.事实上，取x=x2n，y=x2n+1，代入(4)式，可得

(5)

现证明d(y2n,y2n+1)⪯d(y2n,y2n-1).若不然，设d(y2n,y2n+1)≻d(y2n,y2n-1)，则有

(6)

(6)式代入(5)式，可得

显然矛盾，因此

d(y2n,y2n+1)⪯d(y2n,y2n-1).

(7)

d(yn+1,yn)⪯λd(yn,yn-1)⪯…⪯λnd(y1,y0)，

d(ym,yn)⪯sd(yn,yn+1)+s2d(yn+1,yn+2)+…+sn-md(ym-1,ym)⪯sλnd(y0,y1)+

s2λn+1d(y0,y1)+…+sn-mλm-1d(y0,y1)=(shn+s2hn+1+…+

sm-nhm-1)d(y0,y1)=shn(1+sh+(sh)2+…+

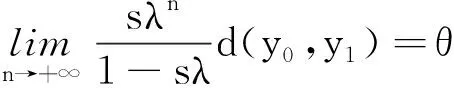
(8)

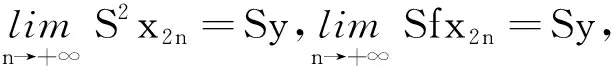
下面取x=Sx2n,y=x2n+1，代入(4)式，可得

(9)

对(9)式取极限，由定理1可得

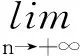
因此d(Sy,y)⪯qd(Sy,y).又由0≤q<1可得d(Sy,y)=θ，于是Sy=y.由映像T连续性，可知

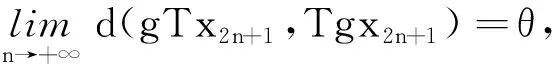
取x=x2n，y=Tx2n+1，代入(4)式，可得

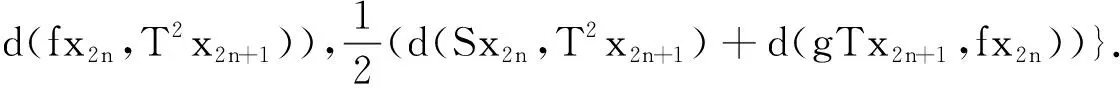
(10)

对(10)式取极限，由定理1可得

因此d(Ty,y)⪯qd(y,Ty)，于是d(Ty,y)=θ，从而Ty=y.

取x=y，y=x2n+1，代入(4)式，可得

(11)

对(11)式取极限，由Sy=Ty=y，可得

因此d(fy,y)⪯qd(fy,y)，于是d(fy,y)=θ，从而fy=y.又由(4)式及Sy=Ty=fy=y，可得

因此d(y,gy)=θ，于是y=gy，从而Sy=Ty=fy=gy=y.

(3)证明y的唯一性.假设y不唯一，即存在x≠y且Sx=Tx=fx=gx=x，则由(4)式可得

于是d(x,y)=θ，即x=y，与假设矛盾，因此y是唯一的公共不动点.

注2由于b-度量空间一定是锥b-度量空间且减弱了压缩条件，因此定理3拓展了文献[16]的相关结果.

推论1设(X,d)是一个完备锥b-度量空间，数量系数s≥1，映像f,g:X→X，对于∀x,y∈X，有

其中0≤q<1，则f，g存在唯一公共不动点.

证明取S=T=I，由定理可3可知f，g存在唯一公共不动点.

推论2设(X,d)是一个完备锥b-度量空间，度量系数s≥1，S,T:X→X是X上的连续自映像，对于∀x,y∈X，有

其中0≤q<1，则S，T存在唯一公共不动点.

证明令f=g=I，由定理3可知S，T存在唯一公共不动点.

推论3设(X,d)是一个完备锥b-度量空间，度量系数s≥1，映像f:X→X，对于∀x,y∈X，有

其中0≤q<1，则f存在唯一不动点.

证明令f=g，S=T=I，由定理3可知f存在唯一不动点.

3 举例

例1设E=R2，P={(x,y)∈E|x≥0，y≥0}，X=[0,1]，d∶X×X→E，定义锥度量d(x,y)=((x-y)2,α(x-y)2)，其中α≥0，则(X,d)为完备锥b-度量空间，s=2.定义压缩映像

及偏序关系(a,b)⪯(c,d)⟺a