DC-投射模的若干注记*

何东林，樊 亮

(陇南师范高等专科学校数学与信息科学学院,甘肃 陇南 742500)

近年来，学者们对Gorenstein同调理论进行了研究和推广.Holm等[1]在交换Noether环上介绍了关于半对偶模C的C-Gorenstein投射模和C-Gorenstein内射模.White[2]进一步研究了交换环上的C-Gorenstein投射模和C-Gorenstein内射模(即GC-投射模和GC-内射模).Gillespie[3]讨论了Ding-投射模和Ding-内射模,此处的Ding-投射模与强Gorenstein平坦模[4]一致,而Ding-内射模与Gorenstein FP-内射模[5]一致.为了研究Ding-投射模和Ding-内射模的可数部分及涉及的模类,Zhang等[6]引入了关于半对偶模C的Ding-投射模和Ding-内射模,分别称之为DC-投射模和DC-内射模.笔者拟研究DC-投射模的若干性质,并讨论与DC-投射模相关的一些模类之间的联系.

定义1[6]称R-模M是DC-投射模,如果存在正合列

例1(1)当C=R时,DC-投射模与Ding-投射模一致.

(2)每个DC-投射模都是GC-投射模.

引理1[6]模类DPC(R)关于扩张、直和、直和因子和满同态的核均封闭.

引理2[6]设M是R-模,则以下条件等价：

(1)M是DC-投射模；

(1)

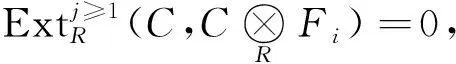
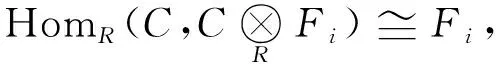
下面对n用数学归纳法证明HomR(C,L)∈T,且自然同态ρL:C⊗HomR(C,L)→L为同构(即L是C-余自反模).

图1 行正合交换1

图2 行正合交换2

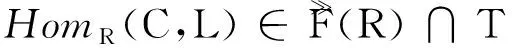
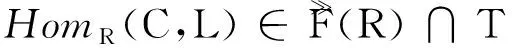
0→Um→…→U1→U0→HomR(C,L)→0,

(2)

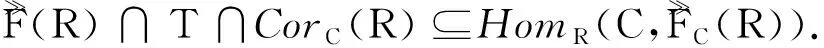
0→Fn→…→F1→F0→L→0,

(3)

(4)

图3 行正合交换3

类似地可证明以下2个结论：

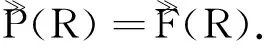
定理5PC(R)是DPC(R)的内射余生成子.