星像函数和凸像函数的逆函数的三阶Hankel行列式*

宋 园

(滁州职业技术学院基础部，安徽 滁州 239000)

1 基础知识

在单位圆盘Δ={z:|z|<1}内，泰勒展式为

f(z)=z+a2z2+a3z3+…

(1)

的解析函数的全体记为T，T中的所有的单叶函数记为S.Noonan等[1]首次引入函数f(z)的q阶Hankel行列式

其中a1=1,m≥1,q≥1.当m,q取一些特殊值时，

于是H3(1)=a3H2(2)-a4(a4-a2a3)+a5H2(1).

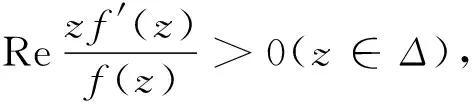
有学者研究了解析函数类T的三阶Hankel行列式[2-5]和单叶函数的逆函数的前几项系数估计或部分二阶Hankel行列式[6-9].笔者拟讨论星像函数和凸像函数的逆函数的三阶Hankel行列式.

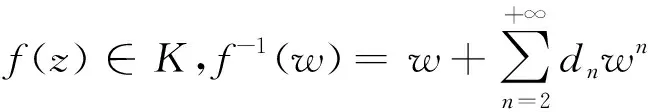
用P表示Δ={z:|z|<1}解析且正实部大于0且具有形式p(z)=1+p1z+p2z2+…的函数类.

引理3[10]若p(z)∈P，则有|pn|≤2(n≥1).

引理4[11]若p(z)∈P，则存在复数x,z(|x|<1,|z|<1)，满足

2 主要结果

证明因为f(z)∈S*，所以存在p(z)∈P，满足

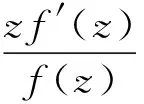
(2)

将(1)式代入(2)式，计算比较z和z2的系数，可得

a2=p1,

(3)

(4)

(5)

(6)

因为

(7)

是f的逆函数，所以

f-1(f(z))=f(f-1(z))=z.

(8)

由(1)，(7)和(8)式，可得

于是

(9)

由(3)～(6)，(9)式，可得

d2=-p1,

(10)

(11)

(12)

(13)

下面估计|d5|的上界.将引理4中p3和p2的值代入(13)式，整理可得

利用三角不等式及|d4|≤2，不失一般性，设|p1|=p∈[0,2],|x|=t∈[0,1]，则有

令

下面讨论G(p,t)在闭区域Ω={(p,t):0≤p≤2,0≤t≤1}上的最大值.令

在边界线p=2上，G(2,t)=43，是一个常数.

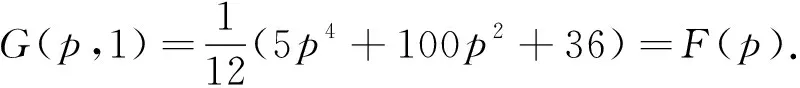
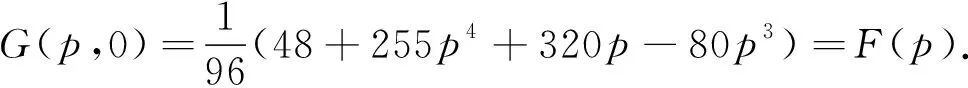
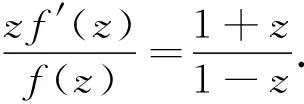
证明由(10)，(11)，(12)式，可得

利用引理2，可得

(14)

因为|p1|≤2，所以假设|p1|=p∈[0,2].令|x|=t∈[0,1]，对(14)式应用三角不等式，可得

和

先求函数G在闭区域Ω={(p,t):0≤p≤2,0≤t≤1}上的最大值.令

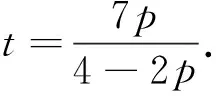
在边界p=2上，G(2,t)=4，是一个常数.

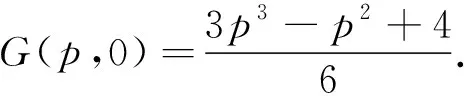
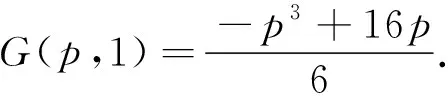
下面求函数F在闭区域Ω={(p,t):0≤p≤2,0≤t≤1}上的最大值.因为

证明由(10)，(11)式和引理4，可得

(15)

因为|p1|≤2，所以假设|p1|=p∈[0,2].令|x|=t∈[0,1]，对(15)式应用三角不等式，可得

证明由引理1、定理1、定理2和定理3，利用三角不等式，可得

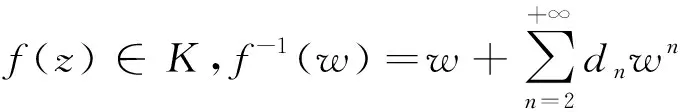
证明因为f(z)∈K，所以存在p(z)∈P，满足

(16)

将(1)式代入(16)式，计算比较z和z2是系数，可得

(17)

由(9)和(17)式，可得

(18)

(19)

(20)

(21)

下面估计|d5|的上界.将引理4中p3和p2的值代入(21)式，整理可得

利用三角不等式和|d4|≤2，不失一般性，设|p1|=p∈[0,2],|x|=t∈[0,1]，则有

令

下面讨论G(p,t)在闭区域[0,2]×[0,1]上的最大值.令

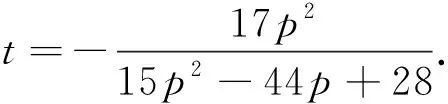
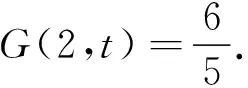
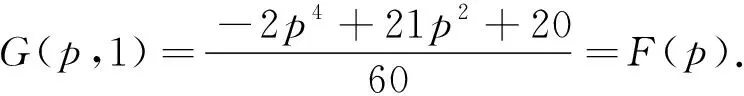
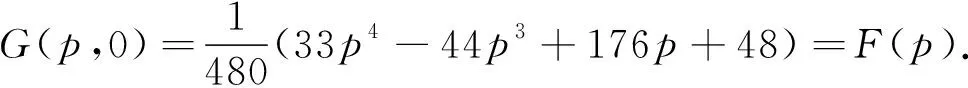
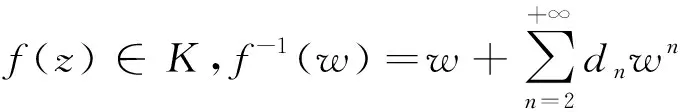
证明由(18)，(19)和(20)式，可得

(22)

由(22)式和引理4，可得

(23)

因为|p1|≤2，所以假设|p1|=p∈[0,2].令|x|=t∈[0,1]，对(23)式应用三角不等式，可得

和

先求函数G在闭区域Ω={(p,t):0≤p≤2,0≤t≤1}上的最大值.令

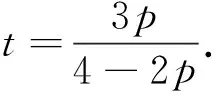
在边界线p=2上，G(2,t)=0.

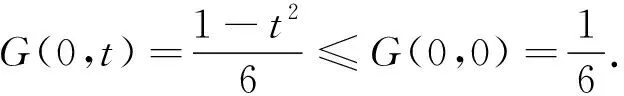
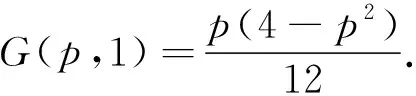
再求函数F在闭区域Ω={(p,t):0≤p≤2,0≤t≤1}上的最大值.对函数F求t的偏导数，可得

于是F关于t在[0,1]上是一个单调递增函数，从而

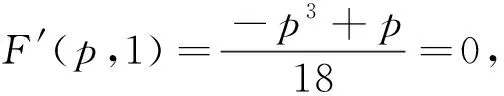
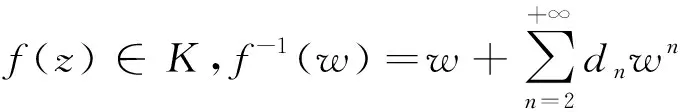
证明由(18)，(19)式和引理4可得

(24)

因为|p1|≤2，所以假设|p1|=p∈[0,2].令|x|=t∈[0,1]，对(24)式应用三角不等式，可得

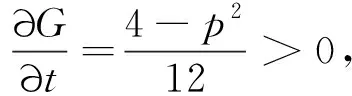
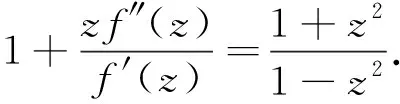
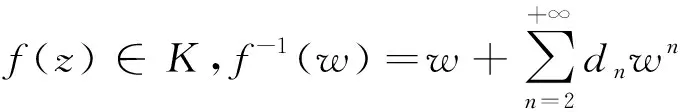
证明由引理2、定理5、定理6和定理7，利用三角不等式，可得