自主创生教学的实践路径

冯桂群 于国海 孙国春

摘要：以“三角形的三边关系”教学为例，探索自主创生教学的实践路径：课前備学中深度卷入，唤醒探究热情;数学操作中深度体验，积累活动经验;多维互动中深度探究，发现数学规律;高阶发展中深度思考，建构认知图式;多元表征中深度运用，提升实践素养;数学反思中深度感悟，明晰人生哲理。

关键词：自主创生;深度学习;小学数学教学

中图分类号：G623.5 文献标志码：A 文章编号：1673-9094（2021）11B-0036-05

纵观当下基础教育课堂，虽然“素养为本”的教育理念已成共识，但是教学中“庸俗化的互动、程序化的合作、肤浅化的探究”依然存在，学生的学习“简单的复制、机械的记忆、肤浅的理解”[1]并未产生本质改变。建构“知、情、意、行、智、思”高度和谐的自主创生教学，是指向学生核心素养发展的实然路径。所谓“自主创生”，是指通过课前备学、问题探究、模式构建、变式应用、思想提炼、哲理感悟等富有张力的数学活动，引领学习者主动、生动、灵动地沉浸于数学学习“再创造”过程，促进学习者数学认知活动发展循着创生阶梯拾级而上，最大限度地释放创造激情，展示创造潜能，诱发迁移创新，塑造创造人格。使学生成为有智性、灵性和德性的创新型人才。自主创生教学的核心是“创生”，关键是“自主”，自主创生教学运行不会停滞于引领层面，也不是满足于形式化、程序化的伪“创生”，而是通过知、情、意、行、智与思的高度和谐，指向“创生”的最高境界。具体的操作框架包括课前备学、数学操作、多维互动、高阶发展、多元表征、数学反思这六大学习环节，它们环环相扣、循环往复、逐步提升。具体实施过程中，六大环节可根据学习内容的难易程度和学生的认知基础进行灵活删减，从而使深度学习的效益最大化。本文以“三角形的三边关系”教学为例，探索自主创生教学的实践策略。

一、课前备学中深度卷入，唤醒探究热情

课前备学是新知学习有效的“导火索”。教者通过巧设备学单，不仅让学生借助操作、练习、调查等活动唤醒相关生活经验和已有旧知，为内化新知打下伏笔，更能在备学中激发问题意识，在认知失衡中点燃探究热情，让学生在新课开始之前就在潜意识里深度卷入对新知探究的渴望之中。

本课教学时，笔者设计的备学单主要内容如下：①剪一剪、围一围、粘一粘：准备3根同样长的吸管，并按要求各自剪成3段后尝试围三角形（将3种情况粘在备学纸的反面）。②关于剪吸管围三角形，你想研究哪些相关的数学问题？试着提出1～2个问题。学生在有趣的备学中既动手又动脑，探究热情一下子就被调动起来了。精彩纷呈的备学作品不仅呈现了他们卷入备学的热情与创意，也体现了他们强烈的问题意识，并反映出共同的思维障碍。比如：在南通市朝晖小学四（1）班的42份备学单中，学生提出的不同数学问题竟有19个，其中有18人提出：“为什么有的剪法能围成三角形，有的不能？”有10人提出：“3根一样长的吸管能拼成三角形吗？”有8人提出：“三角形的三边关系是怎样的，三角形的三角和是多少？”从学生的提问中发现：学生的最大认知困惑是“为什么两边之和等于第三边时不能围成三角形？”。根据备学中收集到的学情，笔者及时调整了学材的内容与呈现顺序，比如：有意添加了教材中没有的“三条边都是6厘米，能否围成三角形”的练习，探究新知时故意先让学生全力探索学习难点“两边之和等于第三边时能否围成三角形”等，从而在以学定教和以教促学中延续学生的探究热情，消除学生的思维误区，为学生的深度学习提供极具针对性和实效性的帮助。

二、数学操作中深度体验，积累活动经验

具身学习观强调：“学习是身体力行的。它需要身体的参与，需要反复实践和亲身经历，不论学习什么，身体在促进学习者的意义理解和反思体验上都发挥着不可忽视的作用。”[2]要想使学生真正理解并内化知识，必须让他们在直观而丰富的数学操作活动中充分经历和深度体验，尤其是在有趣的数学想象、猜想、实验、验证等活动中完整地经历知识产生、发展与变化的全过程，积累活动经验。

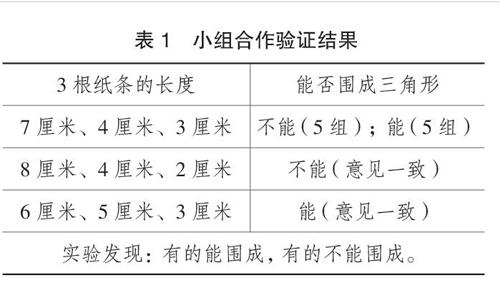
本课开始，笔者先组织学生玩3组“剪纸条”的想象游戏：①想象一根长14厘米的纸条，在纸条的中点剪一刀，再将其中的一段分成2小段，使这2小段的长相差1厘米，剪成的3段分别长多少？（多媒体动态呈现剪纸条的过程和结果：7厘米、3厘米和4厘米。）②仍是14厘米长的纸条，想象如果离纸条中点偏右1厘米处剪一刀，再将其中短的一段分成2小段，使这2小段的长相差2厘米，剪成的3段分别是多少？（同上，结果为：8厘米、4厘米和2厘米。）③仍是14厘米长的纸条，想象如果离纸条中点1厘米处剪开，再将其中长的纸条分成2小段，使这2小段相差2厘米，剪成的3段分别长多少？（同上，结果为：6厘米、5厘米和3厘米。）之后立刻追问：大胆猜一猜，这3组纸条中，哪组纸条能围成三角形？如何验证？于是以小组为单位进行“剪一剪、围一围、填一填、说一说”的验证活动，之后全班交流验证结果（表1）。

无论是备学中剪吸管，还是课上剪纸条，都强调了要从被剪物体的中点或离中点不远处剪开，并且都对应3种情况：两短边之和等于第三边，两短边之和小于第三边，两短边之和大于第三边;所不同的是，课上的想象操作与验证操作中出现了精准的数据。对比明显、结构性强、数据精确、活动充分的剪围游戏，不仅再次激起了学生的探究欲望，丰富了深度体验和活动经验，积累了鲜活的操作表象，更为后面借助鲜明对比、精准计算和合情推理来研究三角形的三边关系和突破学习难点等，打下了扎实的感知基础，成为学生由动作思维引发形象思维与抽象思维的先决条件。

三、多维互动中深度探究，发现数学规律

新课程背景下的课堂教学特别强调师生、生生之间的合作沟通与交往互动。为此，教师应着力引导学生进行四方面的多维互动：学生与文本互动，学生与小组成员互动，学生与全班互动，学生与自己内心互动。在步步深入的多维互动中，探究活动由试误走向创新、由表象深入本质，数学思维也由单一走向发散、由发散走向聚合，学生不仅从中感悟到数学规律的神奇魅力，更提升了数学思维品质和关键能力。

例如在剪纸条围三角形的操作活动中，学生凭直觉就能发现第2种情况肯定不能围，第3种情况肯定能围，但對第1种情况，学生分歧很大。为此，笔者及时组织生生、师生间的集体互动与思维碰撞，在多向交流中深入浅出地攻破思维迷阵。首先，笔者借助多媒体的动态呈现，有序展示7厘米、4厘米和3厘米这3条线段由“首尾不相接”到“快要首尾相接”的奇妙画面，同时启发学生想象出连接起来的两条短边与最长边的位置关系（完全重合）。然后顺势引导学生在“数形结合”中自发概括出：两条短边的和正好等于最长边时（4+3=7），三条边根本不能围成三角形。难点突破后，引导学生在直接观察与类比迁移中发现：第2种情况中，4+2<8，肯定不能围成三角形;而第三种情况，5+3>6，肯定能围成三角形。之后，继续在互动中进行推想和计算并发现：既然两短边之和都比最长边要长，那最长边加上其中一条短边，结果肯定比第三边要长（6+5>3，6+3>5）。由此发现，在三角形中，任意两边长度的和大于第三边;及时引导逆向思考后又发现“第三边小于其余两边长度的和”。至此，认知误区被消解，数学规律被及时发现，知识碎片被巧妙地结为知识网络并被内化，探究活动真正得到深化与活化。

四、高阶发展中深度思考，建构认知图式

指向深度学习的课堂教学，要引导学生快速穿越“浅层学习的感知、记忆、模仿”等低阶层面，高效进入以“推理、分析、探索、创生”为特征的高阶思维层面，在深度思考中领悟数学知识的本质内涵，感悟数学思想的深邃与价值，建构结构化的认知图式，培育数学核心素养。

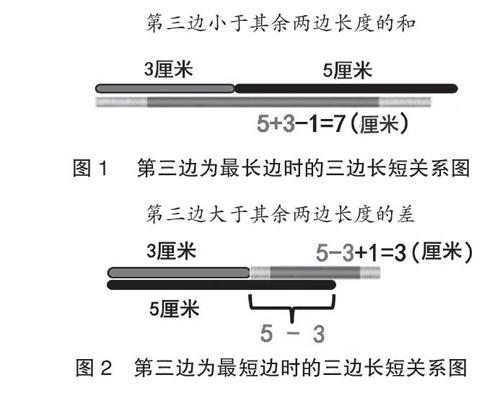
在本案例的上一个环节，学生自主发现了两条短边之和大于第三边，又借助计算和推想发现了“三角形中任意两边长度之和大于第三边”，最后通过逆向思考还发现“第三边小于其余两边长度的和”。显然，这样的学习深度还不够，还需让学生借助高阶思维向知识更深处漫溯。为此，在基础练习之后，笔者创设了一个图文并茂的推理与创生情境：孙悟空有一根能伸能缩、变幻无穷的金箍棒，现在，他想用3厘米、5厘米的小棒和这根金箍棒围成一个三角形，那这根金箍棒最长（整厘米数）可以是多少？最短呢？为什么？学生在独立思考、小组合作和全体交流中，借助观察直观图示，尤其是借助想象、分析、对比、推理等高阶思维活动，很快发现了其中的奥秘：如图1，如果第三边是最长边，因为第三边要小于两边之和，所以第三边最长是3+5-1=7（厘米）。相反，如图2，第三边是最短边时，再短也不能等于或小于其余两边之差，因为如果这样，两短边之和就等于或小于最长边了。所以，第三边最短也要大于其余两边之差，结果是5-3+1=3（厘米）。至此，学生在想象、推理、分析、综合、创造等高阶思维的帮助下，头脑里已经生动鲜活、层层深入地建构了“三角形三边关系”网络化、结构化、关联化的知识图式，即：三角形中，两条短边之和大于第三边，任意两边的长度之和大于第三边;反过来，第三边不但要小于其余两边之和，还要大于其余两边之差;同时，学生的想象力、推理力和创造力等高阶思维力也得到了锤炼，使深度思考真正发生。

五、多元表征中深度运用，提升实践素养

实践运用是巩固知识、发展素养的必经之路。指向深度学习的知识运用教学，重在引导学生借助动作表征、形象表征、言语表征和符号表征等，让思维在具象、形象和抽象间顺逆穿梭、自由跳跃、灵活转换，进而在提升数学理解力和执行力的同时提升实践素养。

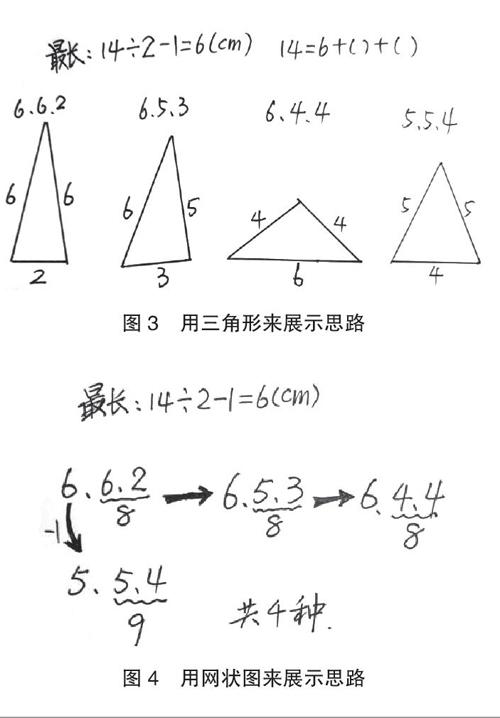
本案例练习环节，笔者带领学生回溯课始的剪纸条游戏，引发他们挑战更开放的数学问题：一根长14厘米的纸条，从中点处剪一刀，最长边是7厘米，这样剪成的3根小纸条是不能围成三角形的。由此看来，最长边如果是整厘米数，最长只能是多少？如何列式？（14÷2-1=6）利用今天所学的知识，你能不再摆学具，而直接借助较直观的数学图形或较抽象的思维导图、言语表述等，将头脑里想到的所有剪后能围成三角形的情况，一个不漏地列出来吗？于是学生以4人小组为单位，饶有兴趣地寻找所有可能的结果。很快，学生们借助画三角形、网状图、树状图等，将所有的答案一一找了出来。以下是3种有代表性的思路表征（图3—图5）：

在此前用吸管或纸条围三角形的具体操作中，学生充分经历了动作表征，在探究活动中又借助图像表征和符号表征建构了关于三角形三边关系的数学模型，所以在实际运用阶段，学生顺利地摆脱了操作层面的动作表征，而直接借助图形表征、符号表征以及言语表征等，多角度展现问题解决的过程与结果，让开放思维与创新思维的过程可视化和多样化，展现了可贵的创新精神和强大的实际运用能力。

六、数学反思中深度感悟，明晰人生哲理

深化课程改革的根本任务是落实“立德树人”的目标，为中华民族伟大复兴培育更多有担当、敢创新的栋梁之材。为此，数学教师在课堂上不仅要对学生进行人文关怀，竭尽全力地将科学、社会、历史、文学、艺术等资源及时融入课堂，更要引导学生借助“数学反思”，去感悟数学学习过程中的理性智慧和人文情怀，明晰人生哲理，树立正确的人生观和价值观，真正提升科学素养、数学素养和人文素养。

比如，在本案例的课始，笔者直接借助一句名言引导学生反思：“爱因斯坦说得好，提出一个问题比解决一个问题更重要。课前备学中，你头脑里冒出的数学问题是什么？”学生自由交流之后，笔者及时肯定：“真善于提问！有疑问才有发现。下面就带着这些问题一起来研究三角形的三边关系。”课中，当学生发现了“三角形的第三边要小于其余两边之和，同时又要大于其余两边之差”时，笔者说：“有句话说得好，没有规矩——”学生接：“不成方圆。”笔者继续提示：“围三角形时，两边之和不符合要求（等于或小于第三边）——”学生回答：“围不成三角形。”笔者又说：“符合要求——”学生说：“就围成了三角形。”笔者做总结：“看来，谁都不可以无法无天、肆意妄为，在图形的王国里也不例外。”学生们听后，大多心领神会地粲然一笑，似有所悟。课尾，笔者则引导学生在回望中反思：“通过今天的学习，你有哪些收获？大家还有哪些想研究的问题？”学生们的提问热情很高，如“三角形还有没有别的性质？”“三角形的三角和有什么特点？”“三角形的面积如何算？”等。笔者接过话茬，意味深长地说：“同学们提的问题都非常好，这些都等待大家进一步去研究、发现，正所谓学无止境。”在以上反思过程中，启发学生爱提问、勤思考，懂得敬畏和自律，保持永无止境的探究热情和创新动力，使“数德”在潜移默化中成为学生核心素养的关键要素。当然，这样的学习反思，还可以延伸到课后，让学生在课余时间写一写近期在数学学习中的感受与体会，在自我反省中“转识成智、化知成德、智德兼修”[2]，并逐渐成长为有德性、有灵性、有悟性的人。

参考文献：

[1]安富海.促进深度学习的课堂教学策略研究[J].课程·教材·教法，2014（11）：59.

[2]于国海.指向深度学习的知识教学——以小学数学为例[J].基础教育课程，2020（11）：40.

责任编辑：贾凌燕

本文获2020年江苏高校“青蓝工程”资助，系江苏省教育科学“十三五”规划课题“基于儿童立场的小学数学‘三动课堂的实践研究”（D/2018/02/295）、教育部职业院校教指委立项课题“‘双考视域下职前教师专业实践素养发展研究”（2020JZWZXXKT31）研究成果。

收稿日期：2021-06-01

作者简介：冯桂群，南通大学教育科学学院（江苏南通，226001）硕士研究生，江苏省南通师范学校第一附属小学正高级教师，主要研究方向为小学数学教育;于国海，南通师范高等专科学校（江苏南通，226001），教授，主要研究方向为小学数学教育;孙国春，南通师范高等专科学校（江苏南通，226001）副校长，教授，主要研究方向为小学教师教育。