基于数理结合的跨学科思维审视高考物理试题

杨培军　王伟民

摘 要：高考评价注重能力考查，掌握科学的思维方法是解决问题的关键.数理结合的跨学科思维的突出特征是思维上融合贯通.以2021年全国物理高考试题为例，分基础型和发展型两类，从数理结合的跨学科思维角度剖析问题，提出合理化的建议.

关键词：思维方法;数理结合;跨学科思维;高考试题

中图分类号：G633.7 文献标识码：B 文章编号：1008-4134（2021）23-0047-04

《中国高考评价体系》明确指出：高考考查的素质教育目标凝炼为“核心价值、学科素养、关键能力、必备知识”的“四层”考查内容.其中“学科素养”承接核心价值的方向引领，统摄关键能力与必备知识;“关键能力”是支撑和体现学科素养要求的能力表征[1].学科素养包括“学习掌握、实践探索、思维方法”三个一级指标，其中“思维方法”是指学习者在面对生活实践或学习探索问题情境时，进行独立思考和探索创新的内在认知品质.“思维方法”是思维品质、方式和能力的综合，是个体高质量地解决生活实践或学习探索情境中的各种问题的基础.思维方法包含三个二级指标：科学思维、人文思维、创新思维[1].科学思维的指标表现是采用严谨求真的、实证的逻辑思维方式应对各种问题.能够根据对问题情境的分析，运用实证数据分析事物的内部结构和问题的内在联系.以抽象的概念反映客观事物的本质特征和内在联系.运用抽象与联想、归纳与概括、推演与计算、模型与建模等思维方法来组织、调动相关的知识与能力，解决生活实践或学习探索情境中的各种问题[1].随着高考评价与教育育人目标的有机联通，需要我们运用融合的科学思维方式去面对，运用好类似数理结合的跨学科思维是值得深入研究、探索的话题.

1 数理结合的跨学科思维的认识

数理结合的跨学科思维是指在物理与数学中不囿于学科边界，重视学科内部、外部的知识交叉、融合，通过跨界去整合知识，从而解决问题的思维方式，它的突出特征是思维上的融会贯通[2].

对于物理学与数学的关系，杨振宁先生曾用长在一棵根茎上的“双叶”加以形容.一片叶子是物理学，另一片叶子是数学，两者生长在同一根茎上，这充分说明了数学与物理学的同源关系.不论物理知识在学习建构过程中，还是物理知识运用过程中，数学和方法论问题都起到重要的纽带作用[3].由于数学方法应用的广泛性、普適性以及数学理性思维的不可替代性，无论是人文社科领域，还是自然科学领域，与数学的交叉与融合都具有普遍性.总之，培养学生数理结合的跨学科思维是非常必要的.由于学科教学的分立，教师教学中过于习惯固守学科边界，很难主动进行学科间知识的融通，造成了思维的局限性.在物理教学过程中，老师要主动示范，引导学生运用数学的思维方法去分析物理概念、规律及物理公式和图像的物理结论，既考虑定性分析，又重视定量计算.真正利用数理结合的跨学科思维让知识之间有了联系，便于迁移，让知识鲜活、流动起来，从而使师生既看见“树木”，又看到“森林”.

2 利用数理结合的跨学科思维分析案例

近几年高考物理重视学生综合素质的考查，试题突出知识间的联系和学科间的融合，以社会生活、生产和科学创新的情境为依托，考查学生能否综合运用学科知识和多种思维方法，从不同角度思考、发现、分析和解决问题.由于物理与数学的密切关系，高考试题的变化倒逼我们加强数理结合的跨学科思维能力的培养，引导学生主动用跨学科思维方法去分析、解决物理问题，更好地达成知识间、能力间的融会贯通.根据数理结合的复杂程度，把相关高考试题分为基础型和发展型，下面结合2021年全国高考物理（乙卷）试题作案例分析.

2.1 基础型

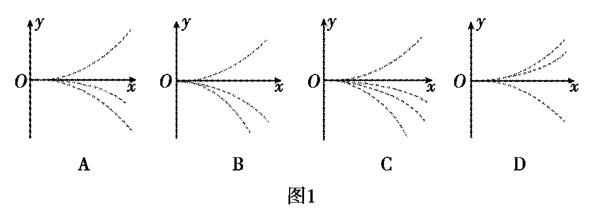
例题1 （2021年全国物理高考乙卷 20题）四个带电粒子的电荷量和质量分别为（+q，m）、（+q，2m）、（+q，3m）、（-q，m）.它们先后以相同的速度从坐标原点沿x轴正方向射入一匀强电场中，电场方向与y轴平行，不计重力，下列描绘这四个粒子运动轨迹的图像中（如图1），可能正确的是分析：该题以不同荷质比的带电粒子在同一电场中偏转为情境设置问题，主要考查学生根据抛体运动规律，确定不同带电粒子运动轨迹图形形状的判断能力.在x轴上粒子的运动位移为x=v0t;在y轴上，粒子运动的加速度和位移分别为a=qEm和y=12at2，所以，带电粒子在电场中运动的轨迹方程为y=qE2mv20x2.由粒子运动的轨迹方程可知，带电粒子运动轨迹的形状与荷质比qm的大小有关.此题需要建构所学抛体运动的轨迹方程，利用数学中的函数图像特点去进行分析、判断.学生如果缺乏建立轨迹方程的意识，没有跨学科思维的习惯，就难以形成解决问题的方法和路径.这类题目在历届高考中也曾反复出现过.

评析：此类高考试题的解答，多从具体物理问题出发，经过知识的梳理需要延伸到利用数学工具去解决.教师在教学中应多引导学生从数理结合的角度，运用联想、类比、迁移、逆向思维等方法去处理物理问题，尤其注重挖掘并发现隐含的数学元素，逐步培养学生运用数理结合的跨学科思维方式去解决相关的物理问题.

2.2 发展型

例题2 （2021全国高考物理乙卷 34题（2））用插针法测量上、下表面平行的玻璃砖的折射率.实验中用A、B两个大头针确定入射光路，C、D两个大头针确定出射光路.O和O′分别是入射点和出射点，如图2（a）所示.测得玻璃砖厚度为h=15.0mm;A到过O点的法线OM的距离AM=10.0mm，M到玻璃砖的距离MO=20.0mm，O′到OM的距离为s=5.0mm.

（ⅰ）求玻璃砖的折射率;

（ⅱ）用另外一块材料相同，但上下表面不平行的玻璃砖继续实验，玻璃砖的截面如图2（b）所示.光从上表面入射，入射角从0°逐渐增大，达到45°时，玻璃砖下表面的出射光线恰好消失.求此玻璃砖上下表面的夹角.

分析：插针法是一种测量结果相对比较精确，而操作过程又非常简单的测量透明物质折射率的实验方法.例题2是2021全国高考物理乙卷选考题最后一题（34题）的第（2）小题，以插针法测量玻璃折射率为背景设置的题目.通过考生对该题目的解答，可以考查学生对折射率的含义、全反射的条件等知识点的掌握情况，以及灵活运用数学知识解决复杂物理问题的能力.

第一问，利用题目给出的相关线段的长度作为条件，在图2（a）Rt△OAM和Rt△OO′N中可以分别求出∠AOM和∠OO′N的正弦值，再根据折射率的定义即可确定组成玻璃砖材料的折射率为2.应该说，题目的第一个小问题属于基础性问题，只要学生掌握折射率的定义，利用题目条件容易确定问题的答案.相比于第一个问题，第二个小问题的难度要高一些，不仅要求学生掌握全反射的条件，而且还要有较强的分析问题和解决问题的能力.根据题目条件，在图中作出相关辅助线之后（如图3）——

可以看出，本题目的两个小问题，不仅考查的知识点全面，而且有明显的难度梯度，具有区分考生能力高下的功能，这也是作为选拔性考试题目应该具备的一个条件.

能够发现，这道高考题目给出的几个长度数据条件比较“特殊”，利用三角函数经过计算刚好使得相关的角度为特殊角（分别是15°、30°和45°这些特殊角），这肯定是编者精心设计的结果，目的是使考生便于根据题目给出的长度数据进行相关角度的计算.我们从数理结合的视角去思考，如果该问题给出线段的长度数据是任意的，对应的相关角度就可能不再是特殊角，那么，一般情形下这一物理问题的求解，在数学关系上是否存在确定的规律？

2.3 扩展条件 寻找规律

例题3 如图4所示，玻璃砖的上下两个侧面PQ和RS不平行，让一束光线按图示方向以较小的入射角从空气照射到玻璃砖上表面PQ上的确定点O，并逐渐增大入射角，发现当入射角增大到θ时，进入玻璃中的折射光线OB射到玻璃下侧面时刚好发生全反射，若玻璃的折射率为n，试求玻璃砖上下两个侧面PQ和RS夹角α的大小（可用反三角函数表示）.

分析：这道高考变式题目，是在原高考题目的基础上更改一些条件之后，将原高考题目给出的特殊角下的物理问题推广到一般情形，各相关角度成了任意角，所以，这道变式题目的解决方法和对应答案更具普遍意义.

该结果正是例题2给出条件下玻璃砖上下表面的夹角，这也从一个侧面说明我们推得的公式α=arcsin1n-arcsinsinθn的正确性.

与原高考题目给出的问题相比，这一变式给出的一般情形下问题的求解，能够更好地利用数理结合的跨学科思维方式培养学生的科学推理能力.

2.4 开拓思路 创编新题

例题4 如图6所示，半球状玻璃砖球心为O，底面水平放置，OM是垂直于底面的直线，玻璃的折射率为233，ON是过O点的另外一条直线，它与OM的夹角为α，在两条直线确定的平面内，光线AB以很小的入射角从空气射向玻璃砖球面上的点B，保持入射点位置不变，逐渐增大入射角，当角度增大到确定值θ时，折射入玻璃砖中的光线再射向底面时刚好发生全反射，已知C是A在直线OB上的正投影，AC=1，BC=2.

（1）求法线ON与直线OM夹角α的大小;

（2）如图7所示，当入射光线ED对应法线OP与竖直线OM的夹角为=15°时，为使折射入玻璃中的光线再射向玻璃砖的底面时能够发生全反射，入射角θ′的最小值为多大（结果可用反三角函数表示）？

解析：（1）图6中过光线AB的入射点B作球面的切线，交底面于S，如图8所示，则∠S=∠BOM=α，由已知条件可求得sinθ=33，则光线从B点由空气入射时，相当于光线从两侧面为平面且夹角为α的玻璃砖的一个侧面由空气入射的情形，运用例题2推导的公式可得

（2）圖7中，对入射光线ED而言，要使折射光线再射到玻璃砖的底面时发生全反射，必须满足：

答：（1）法线ON与直线OM夹角α的大小30°;（2）为使折射入玻璃中的光线再射向玻璃砖的底面时能够发生全反射，入射角θ′的最小值为θ′=arcsin63.

评析：上面给出的高考试题原题和对应变式的解答，能够利用数理结合的跨学科思维方式解决相关问题，从例2到例3，体现了归纳推理的基本思想，从例3到例4，展现了演绎推理的思维方式，这些问题的解决可以提升学生的科学推理能力.教师要有对此类高考题背后的数学规律挖掘的意识和行为，多带领学生灵活使用数理结合的跨学科思维去深化对物理规律的认识，引导学生思考知识内部的关联规律，提升学生深度分析问题的能力[4].

3 结束语

数理结合的跨学科思维立足于运用物理知识，结合数学工具去解决相关的实际问题，既要考虑物理条件的约束，又需注意数学处理时的边界问题，这对教师的专业素养提出了更高的要求.建议教师在业余时间多学习数学教材的相关内容，经常与数学教师沟通交流，找准数理结合显性和隐性的“链接点”.教师应身体力行，言传身教，在平时的教学过程中，尤其是习题课教学时，应引导学生有意识地运用数理结合的跨学科思维解决相关的物理问题.

参考文献：

[1]教育部考试中心.中国高考评价体系[M].北京： 人民教育出版社，2020.

[2]黄翔，童莉，史宁中.谈数学课程与教学中的跨学科思维[J].课程·教材·教法，2021，41（07）：106-111.

[3]邢红军.中学物理教学法[M].北京： 北京大学出版社，2020.

[4]杨培军.追根溯源 瑕不掩瑜——2016年高考全国卷Ⅰ物理第35题赏析[J].物理教师，2017，38（01）：81-83.

（收稿日期：2021-09-03）

基金项目：安徽省教育科学研究项目2020年度课题“新人教版高中物理单元教学设计的实践研究”（项目编号：JK20040）;人民教育出版社课程教材所“十三五”课题“基于智慧课堂的新版高中物理实验教学的实践研究”（项目编号：KC2020-007）.

作者简介：杨培军（1970-），男，安徽阜阳人，本科，中学高级教师，物理教研员，研究方向：课堂教学;

王伟民（1964-），男，安徽阜阳人，本科，中学高级教师，研究方向：中学物理教学.