基于SRCKF的电动汽车锂离子电池荷电状态估计

肖仁鑫，李 斌，黄志强，贾现广

(1.昆明理工大学交通工程学院，云南昆明 650500；2.云南中石油昆仑燃气有限公司，云南 昆明 650000)

电池荷电状态(state of charge,SOC)估计用于估算汽车剩余续驶里程[1]，其可以提高电池的安全性、延长电池的寿命[2]。电池模型的选择很大程度上决定着电池状态的可靠性和估计精度。

广泛使用的电池模型有电化学模型、智能数学模型、等效电路模型等[3]。电化学模型由于状态估计时收敛性差，结构复杂，因此实用性不强；智能数学模型通常使用人工智能数据驱动的方法，能自适应学习模型参数不确定的情况，但由于使用复杂而不适合工程应用；等效电路模型运算量小、实时性好和鲁棒性好，由于二阶RC 等效电路模型具有电池的欧姆内阻特性和极化特性，本文采用二阶RC等效电路模型。

SOC通常用来表征动力电池的剩余电量，常用的SOC估计方法有库仑计数法、基于特征参数的方法和基于模型的方法。库仑计数法由于简单容易实现而在BMS 中广泛应用，但电池老化和容量的衰减会导致误差和精度；基于特征参数的方法主要有内阻法和开路电压法等，但该方法静置时间长，因此不适合在线估计；基于模型的方法精度高、实时性好，其方法通常结合电路模型与滤波算法使用[3]。

通常，采用电化学阻抗仪实验和基于模型辨识的方法，可以得到电池模型参数，其中，阻抗仪实验时将不同频率的小幅交流电流输入电池，阻抗仪根据测量相应输出电压绘制出其交流阻抗谱图，由交流阻抗谱在不同频率点上阻抗特性分析计算得到电化学参数。这种方法实验量大，需要专业的测量仪器，但电池参数会随着其使用温度、寿命等发生变化。该方法得到的测量值不能根据电池状态变化，难于反应其真实状态；基于模型辨识法结合特征实验和在线辨识的方法可实时更新电池参数。

容积卡尔曼滤波(cubature Kalman filter，CKF)比无迹卡尔曼滤波(unscented Kalman filter,UKF)的计算量要少，且CKF 容易受到不准确的初始差分和扰动的影响，为了避免滤波发散对系统稳定性造成的影响，本文采用平方根容积卡尔曼滤波(SRCKF)算法估算电池SOC[4]。SRCKF 使用协方差矩阵的平方根形式进行迭代更新计算，从而消除滤波器在计算中的发散[5]。

1 电池建模与参数辨识

1.1 电池等效模型

本文采用二阶RC 等效电路模型，如图1 所示。

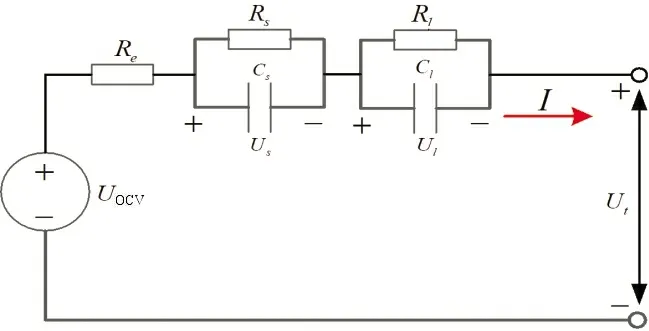
图1 电池二阶RC等效电路模型

该模型采用两个串联的并行RC 环(RlCl和RsCs)来描述动力电池工作过程中所产生的极化特性。该模型采用基尔霍夫定律求解电路方程为：

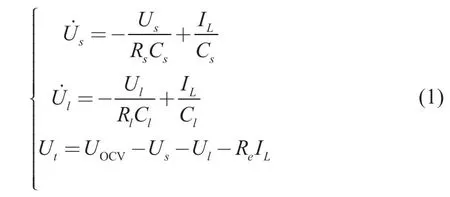
式中：Ut、IL、UOCV分别为k时刻的端电压值、载荷电流和开路电压；Rl和Cl、Rs和Cs为两组电池极化参数，分别用来表征电化学极化内阻、电化学极化电容、浓差极化内阻、浓差极化电容；Re为电池内部欧姆内阻；Us、Ul分别为RsCs环和RlCl环上的电压。

本文运用混合动力脉冲能力测试(hybrid pulse power characteristic,HPPC)对其进行试验，试验对象是标称容量为2.55 Ah、标称电压为3.6 V 的锂离子电池。图2 为电池HPPC试验充放电策略及相应的电压响应曲线。式(2)为电池开路电压(open circuit voltage，OCV，其值为UOCV)和SOC之间的关系。图3 为OCV与SOC的关系曲线。

图2 电池HPPC试验充放电策略及相应的电压响应曲线

图3 OCV与SOC的关系曲线

1.2 等效电池模型的数学形式

把电池模型转换成可应用最小二乘法辨识的数学形

式[7]，将式(1)用频域表达式表示为：

式中：E(k-1)、E(k-2)分别为k-1、k-2 时刻的端电压与开路电压的差值；IL(k)、IL(k-1)、IL(k-2)分别为k、k-1、k-2 时刻的输入电流。

令a=Re，b=τlτs，c=τl+τs，d=Re+Rl+Rs，f=Reτl+Reτs+Rlτs+Rsτl，因此，a、b、c、d和f可用辨识参数θ1、θ2、θ3、θ4、θ5表示为：

1.3 参数在线辨识

根据最小二乘基本原理：

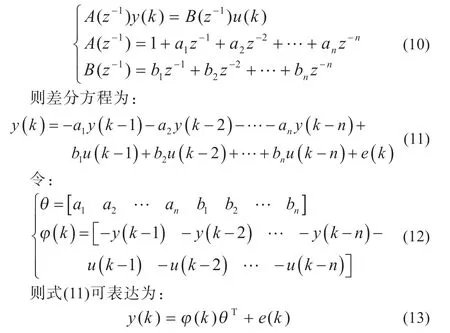
式中：y(k)为在k时刻的测量值或观测值；θ 为参数矩阵；e(k)为k时刻的误差；将系统扩展至N维，即k=1,2,…,N+n，则：

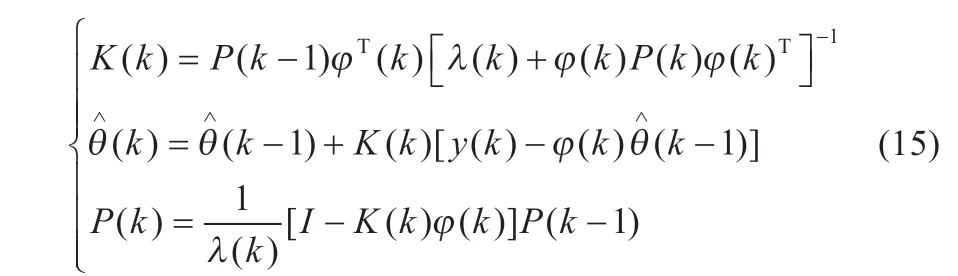
稳态时，遗忘因子λ 接近或等于1，当在线辨识参数误差很大时，需要优化遗忘因子，从而减少辨识误差，使在线辨识具有更快的收敛速度。为了达到上述目的，提出计算自适应遗忘因子的公式为：

式中：λmin为遗忘因子最小值，为了权衡辨识等效电路的快速性和准确性，本文取常数0.98。h为敏感系数，表征遗忘因子对误差的敏感性，为了在参数辨识的精度和响应速度之间平衡，本文选择h为0.9。e(k)为k时刻误差，ebase为允许误差参考值，round(n)为最接近n的整数。当k时刻误差e(k)大于ebase时λ快速减小，当k时刻误差e(k)小于ebase时，辨识参数是稳定的，λ快速变大。从式(16)可得，本方法可以根据辨识参数的误差自适应地调整遗忘因子。电池模型参数进行在线辨识的流程图如图4 所示。

图4 自适应遗忘因子递推最小二乘法算法流程图

根据上述的AFFRLS 理论推导过程，本文采用DST 工况实验获得的实验数据进行参数辨识，得出其结果，为了得到其真实参数，通常在辨识达到稳态之后，用稳态状态下一定窗口范围内估算参数的平均值作为其真实值。图5 为电化学极化内阻Rl；图6 为电化学极化电容Cl；图7 为浓差极化内阻Rs；图8 为浓差极化电容Cs；图9 为欧姆内阻Re。从图中可以看出，经过初始几次振荡后，待辨识参数均能很快收敛到电池真实参数。

图5 电化学极化内阻辨识结果

图6 电化学极化电容辨识结果

图7 浓差极化内阻辨识结果

图8 浓差极化电容辨识结果

图9 欧姆内阻辨识结果

在模型参数辨识后，本文使用DST 工况测试所获得的实验数据，验证辨识结果及模型的准确性，通过实测端电压与模型输出的端电压的差值来对模型性能进行评价。图10 为DST 工况下实测端电压与模型输出端电压对比；图11 为DST工况下端电压对比误差。

图10 中局部放大图表明端电压的实测值和估计值之间的差距非常接近。从图11 中得出，两者之间的绝对误差在20 mV 以内，说明本模型具有较高的精度，能够表达电池的动态特性。

图10 DST工况下实测端电压与模型输出端电压对比

图11 DST工况下端电压对比误差

2 基于SRCKF 的锂离子电池SOC 估计

首先推导SRCKF 的原理，然后将其应用于锂离子电池SOC估计中，并将SRCKF 算法与传统的UKF 算法进行SOC估算对比分析[8]。

2.1 平方根容积卡尔曼滤波的SOC 估计

SRCKF 算法具体实施步骤如图12 所示。首先建立非线性系统方程，对状态量、误差协方差Pk，初始化得出P0|0，Q为过程噪声协方差，R为测量噪声协方差，m表示状态量的维数,N为仿真总步长并计算初始容积点数集ξj,SQ是状态噪声协方差矩阵Qk的均方根值为加权中心矩阵；第一步是时间更新，计算容积点Xi,k-1|k-1，状态方程传播得到的容积点，k时刻状态量预测值，k时刻误差协方差矩阵的平方根Sk|k-1；第二步是测量更新，重新计算容积点Xi,k|k-1，测量方程传播得到的容积点Zi,k|k-1，计算k时刻的测量预测值，计算测量误差协方差平方根Szz,k|k-1，计算状态预测值和测量预测值之间的协方差Pxz,k|k-1；第三步是状态估计，计算卡尔曼增益Wk，状态量估计值，误差协方差平方根估计值Sk|k。

图12 基于SRCKF的锂离子电池SOC估计

使用SRCKF 算法估计锂离子电池SOC，离散化状态方程和测量方程分别表示为：

式中：Δt为采样时间间隔，τs=RsCs，τl=RlCl为时间常数；Ca为锂离子电池可用容量；Ut,k、UOCV,k、Ik分别为k时刻的端电压值、开路电压和载荷电流，Us,k、Ul,k分别为k时刻RsCs环和RlCl环上的电压估计值。其中系统状态变量为xk=[Us,k Ul,k SOCk]T，输入变量为uk=IL,k，输出变量为zk=Ut,k。

2.2 验证分析

为了对本文所使用的SRCKF 算法估算SOC的效果进行验证和评估，在使用AFF-RLS 算法对参数进行在线辨识的基础上，采用电池试验获得的DST 工况下的实验数据，将SRCKF算法与UKF算法估算的SOC进行对比[9]。图13为DST 工况下SOC对比曲线，从图的局部放大图中可得，与真实的SOC估算曲线相比，SRCKF 估算的SOC曲线更接近真实值。图14 为DST 工况下SOC估计误差曲线，从图中可看出UKF 算法在SOC估计的前期波动是因为状态变量跟踪滞后导致估算误差较大，趋于稳定后，SRCKF 算法的最大绝对值误差为0.458 1%，与UKF 算法最大绝对误差的0.986 8%相比，误差小、精度高。图15 为DST 工况下不同初始值的SOC对比曲线，当初始SOC为0.8 时，SRCKF 算法能够较快地收敛到SOC真实值附近，说明该算法具有很好的鲁棒性和收敛性。

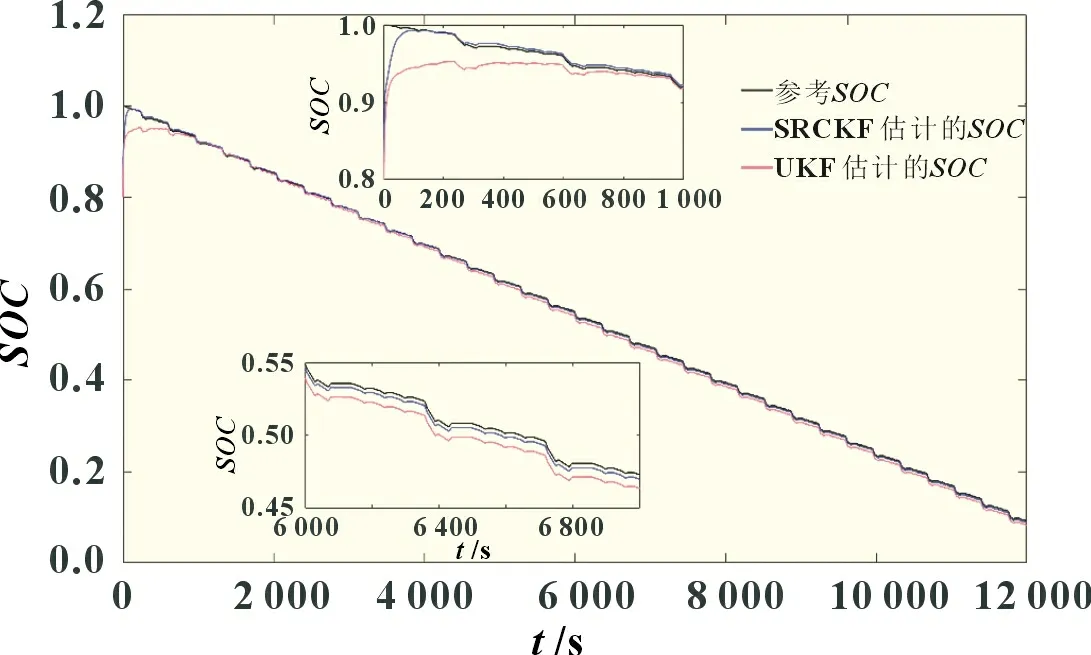
图13 DST工况下SOC对比曲线

图14 DST工况下SOC估计误差曲线

图15 DST工况下不同初始值的SOC对比曲线

3 结论

本文建立了二阶RC 等效电路模型，采用自适应遗忘因子递推最小二乘法在线辨识模型参数，使用DST 工况实验数据，通过实测端电压与模型输出端电压的差值验证了模型的准确性；在DST 工况条件下，基于平方根容积卡尔曼滤波算法估算电池SOC，并与UKF 估算的SOC进行对比，结果表明，SRCKF 误差小、精度高、鲁棒性好，因此具有更好的实用性。