教育神经科学视野下的研究性单元整体教学设计
吴增生




摘 要:教育神经科学是一门新兴学科,它综合运用生物学、神经生理学、神经心理学、认知神经科学、发展与教育科学的视角和方法研究教育活动. 用教育神经科学的视野分析和研究几何教学,创新发展学生空间观念、几何直观和推理能力的教学策略——融合直观与逻辑的研究性单元整体教学.应用这一策略整体设计“相交线与平行线”教学框架,开发教学案例,为进一步把这种策略应用于课堂教学提供可参照的教学设计样例.
关键词:教育神经科学;研究性单元整体教学;案例设计
教育神经科学是综合运用生物学、神经生理学、神经心理学、认知神经科学、发展与教育科学的视角和方法研究教育活动的一门新兴学科. 它从基因、分子、突触、神经元、神经网络、神经系统、课堂行为等不同层面揭示学生学习行为产生的完整过程,以对学生的学习行为提供因果解释,研究学习和教育的规律. 随着认知神经科学的发展,对数学学习行为的脑内神经网络及其活动的研究成果越来越丰富. 近二十年来,下列领域的研究取得了大量成果:支撑数学认知加工的核心神经网络研究,包括视觉空间和数量加工神经环路、语义环路、情境环路的研究;空间与數量整合的“心理数轴”研究;空间视觉背侧与腹侧通路的分工协作并协同海马区(特别是海马旁回位置区)对物体的位置、形状、大小、运动等加工机制研究;推理的神经机制研究;问题解决的神经机制研究;情绪加工的神经机制研究;等等. 这些研究成果为改进数学教育提供了比较坚实的科学理论基础.
基于这些研究成果,结合对几何研究思想的分析,笔者提出了“融合直观与逻辑的研究性单元整体教学”的几何教学策略,具体如下:① 创设适当的情境引入研究对象,明确研究问题,体会研究价值和意义;② 用图形研究的“大观念”引领整体规划研究主线;③ 加强直观与逻辑的融合;④ 引导学生从一般到特殊,从定性到定量地研究几何图形及其关系;⑤ 分散和集中相结合,训练学生的空间想象能力和逻辑推理能力;⑥ 创造促进学生学习的情绪环境.
所谓研究性单元整体教学,指的是以主题研究为核心设计研究主线,引导学生自主研究,通过主题研究获得知识,体会数学思想方法,积累数学活动经验,发展数学学科核心素养. 这种教学策略有两个最显著的特点:一是研究性,具有明确的研究主题和研究主线;二是整体性,关注知识的整体建构. 下面以人教版《义务教育教科书·数学》七年级下册第五章“相交线与平行线”为例(不包括平移),说明这种研究性单元整体教学是如何设计的.
一、分析内容逻辑结构,构建单元研究主题与研究主线
初中几何是小学实验几何到推理几何的发展,研究方法从直观方法发展到基于直观的逻辑方法. 用逻辑推理的方法研究几何,是以概念和公理(基本事实)为基础,从点、线、面等基本要素出发,构建几何对象并研究其性质. 在七年级上学期,学生已经经历了从实物中抽象出几何图形,分离出构成几何图形的要素——点、线、面,学习了直线、射线、线段和角等相关知识,形成了几何基本概念体系,研究了点与直线的位置关系,定义了相交线.
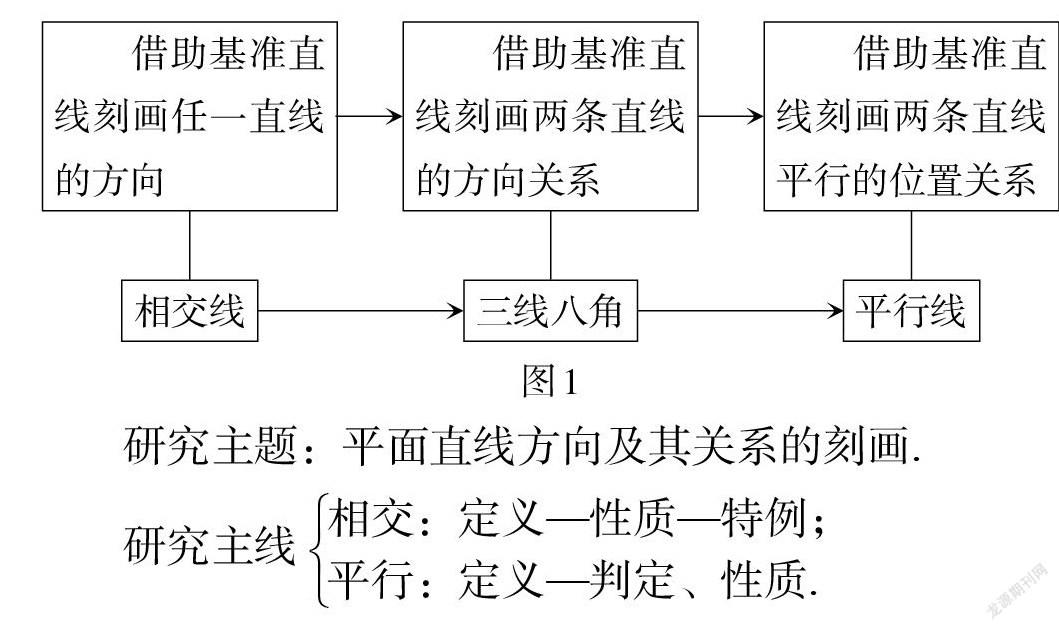
在这些学习的基础上,本章重点研究平面上两条直线之间的位置关系——相交与平行. 直观地看,在平面上任意画两条直线,一般来说是相交的,平行是其特殊情况. 那么,为什么要研究相交线与平行线呢?根据格式塔原理,人们会把互相平行的线条知觉为一个整体,其认知神经学依据是空间视觉神经网络中方向感知神经元按照方向分类激活这一原理. 研究相交线是借助基准直线刻画一条直线的方向的需要,引入“三线八角”是借助基准直线刻画直线之间不同方向关系的需要,平行线的研究则是借助基准直线刻画直线平行(同向)关系. 到高中阶段,进一步用向量共线来刻画两条直线同向.
因此,相交线与平行线研究的核心问题是:如何借助基准直线刻画平面内任一直线的方向;如何借助基准直线建立判断平面内两条直线是否相交的准则(如同位角不相等,两直线相交;同位角相等,两直线不相交,即同位角相等,两直线平行). 研究的主线是:先研究相交线(包括“垂直”特例),再研究平行线. 知识发生、发展的逻辑关系和研究主线可用图1表示.
研究主题:平面直线方向及其关系的刻画.
研究主线[相交:定义—性质—特例;平行:定义—判定、性质.]
二、分析课程标准,明确单元教学要求
分析《义务教育数学课程标准(2011年版)》对图形与几何领域的整体目标,可以明确其整体目标是:发展空间观念,建立初步的几何直观,发展推理能力.
对于“相交线”的内容目标较多,目标层次也有所不同,需要融入主题研究的各种活动中. 例如,在相交线的研究中,通过画图、想象和推理,学习邻补角和对顶角的性质,学习垂线的相关概念、事实;基于平行线的直观经验,基于想象和操作确认获得平行线的基本事实,进而通过推理证明得到平行线的判定和性质定理. 在这些学习活动中发展空间观念、建立几何直观、发展推理能力. 这些目标在本单元内容中的定位如图2所示.
动态感知与想象——空间观念;用角刻画直线的方向及其关系——几何直观;发现、提出和证明命题——推理能力.
三、分析学情,为设计合理的教学方案奠基
对直线、角的概念及其方向差含义的理解是学习相交线与平行线内容的基础. 因此,理解直线的本质是“点沿着一个固定方向无始无终地无限运动”得到的对象,直线具有方向性,可以用方向和点刻画直线,这对学习相交线与平行线是至关重要的. 实际上,对直线方向及其连续变换的视觉感知具有特定的脑神经网络支持,垂直的特殊性及应用的广泛性是基于大脑对水平和纵向线条的空间视觉的敏感性,平行则是基于大脑对相同方向线条的视觉感知的神经网络的重叠,同一方向激活相同的神经元群. 充分利用大脑的这些认知神经机制,可以改进相交线与平行线的教学. 其关键是以下三个方面. 第一,先用动态图形引发学生的线条方向空间视觉,发展空间观念;在此基础上用角进行量化刻画,建立空间与数量之间的联系. 如果学生在七年级上学期的学习中没有建立直线方向的空间运动知觉,没有理解角度刻画方向的功能,则在本单元内容的直观感知中会遇到困难. 第二,对“三线八角”的空间结构理解困难会导致学习平行线性质和判定的困难. 第三,学生演绎推理的经验少,对演绎证明的必要性和表达方式难以理解,特别是对命题的题设和结论区分困难,这也是学习的难点. 用直线的动态旋转建立方向直观,用角度刻画方向,借助基准直线刻画直线的方向,理解“三线八角”的空间结构,通过类比、说明和举例,帮助学生区分命题的题设和结论,理解演绎证明的逻辑语言体系. 这些是帮助学生突破难点的基本策略.
四、设计教学活动框架
基于以上分析,考虑以“如何刻画平面上直线的位置及其关系”为研究主题,创设情境,引入研究对象、提出研究问题、规划研究主线;分“相交”和“平行”两个阶段分步实施,构建整体逻辑体系.“相交线”研究的核心问题是如何借助基准直线用角度刻画一条直线的方向;“平行线”研究的核心问题是借助基准直线用角度刻画两条直线方向之间的关系,得到平面内两条直线是否相交(平行)的判断准则(充分必要条件). 这里渗透了共线向量的含义.
1. 整体规划——创设情境,引入研究对象,提出研究问题,规划研究主线
(1)从现实情境中抽象出相交线与平行线.
基于现实情境:从围栏和高楼立面的横纵线条形象(图3和图4)抽象出平面内直线之间的位置关系——相交(包括垂直)和平行. 基于方向建立相交和平行的直观理解:直线方向相同——平行;直线方向不同——相交,直线方向用从左向右的方向定义. 这是基于视线条朝向知觉原理设计的教学活动(详见文[20]).
(2)基于直观,提出研究问题.
水平直线和竖直直线很容易分辨,但倾斜的直线怎样刻画?
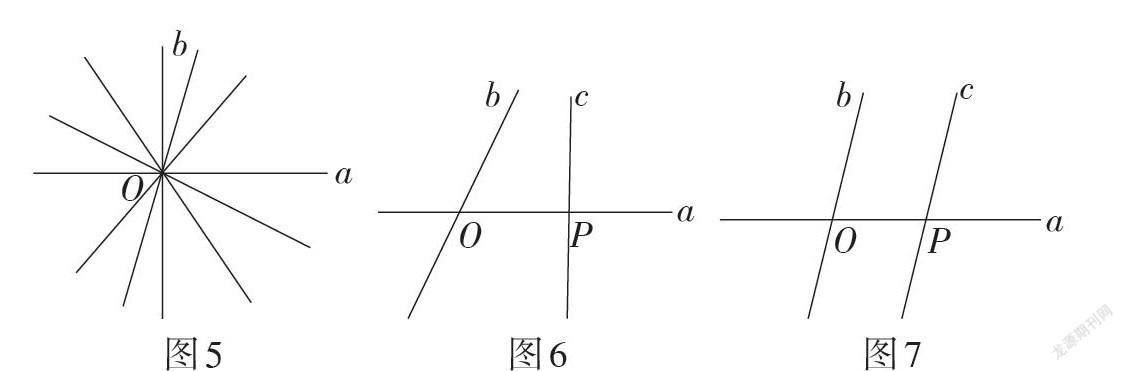
① 已知一条直线b及其上的一点O,想象直线b的不确定性,说出直线b的位置变化,并动态展示其变化过程——旋转改变方向,而要刻画这些直线的差异,需要以一条直线a为基准,研究不同的直线与基准直线的方向差异(如图5),这就是相交线要研究的问题.
② 任意一条直线的方向可以借助基准直线进行刻画,那么两条直线的方向关系怎样刻画?引导学生考虑用共同的基准直線a刻画直线b,c的方向(分别在直线b,c上画点O,点P,过点O,P作直线a)(如图6);固定直线b,绕点P旋转直线c,发现会出现直线c与直线b平行(不相交)的情况(如图7). 进一步,引导学生提出本单元研究的核心问题:借助基准直线刻画任意一条直线的方向,研究两条直线的方向之间的关系(方向不同——相交;方向相同——平行).
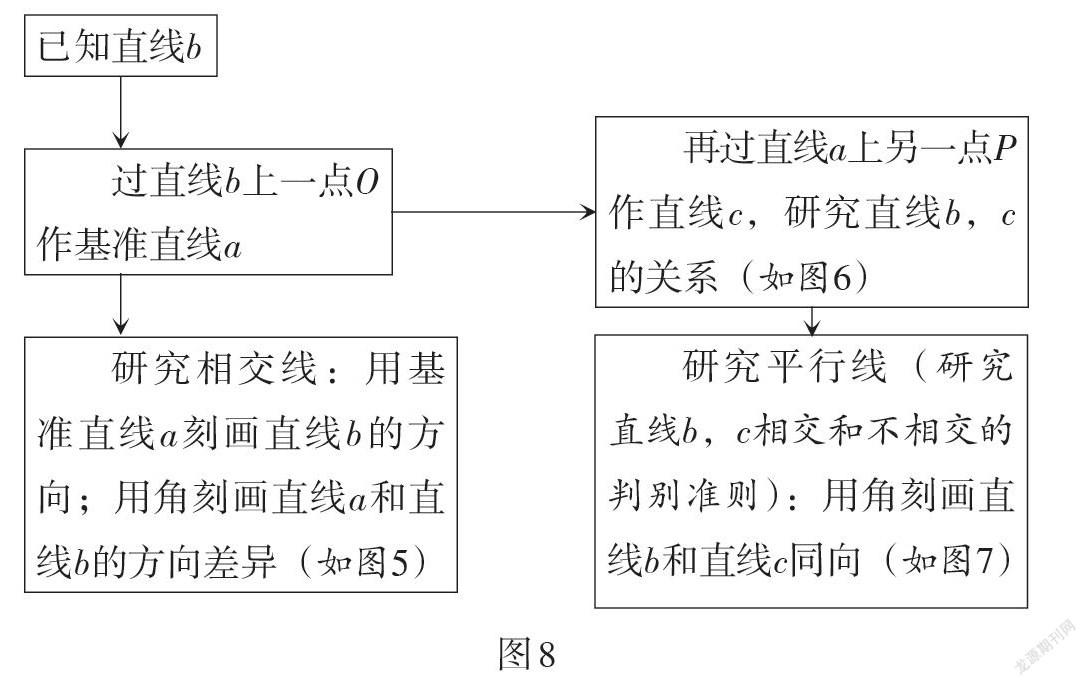
(3)规划研究主线.
引导学生回顾角的概念及本质,让学生明确本单元研究的主要问题:用角及其关系刻画同一平面上直线的方向及其关系(包括相交和平行). 规划研究主线如图8所示.
2. 分步实施1——用基准直线刻画一条直线的位置
(1)建构图形.
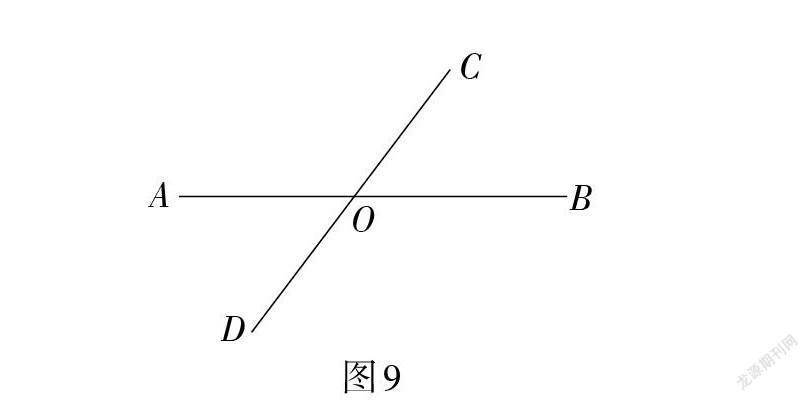
简化图5得到图9,构建相交线的简约图形.
(2)提出问题.
引导学生提出问题:怎样刻画直线AB和直线CD的方向差异?即开口大小(可以用剪刀作为现实直观模型)——用角刻画.
(3)分析问题.
首先是找角,发现有四个角,产生疑问:用哪个角刻画方向的差异?进一步转换问题:研究四个角∠AOC,∠COB,∠BOD,∠AOD之间的关系,用位置关系来定义邻补角和对顶角,研究角的数量关系.
(4)解决问题.
分析四个角的位置关系,引入邻补角、对顶角的概念,明确其空间结构特点;分类研究邻补角和对顶角的数量关系,通过推理得到结论:邻补角互补;对顶角相等. 进一步明确,如果∠AOC的大小确定(度数为[α°]),则∠COB,∠BOD,∠AOD的大小也唯一确定(度数分别为[180-α°,α°, 180-α°]),所以可以用其中任意一个角的大小来刻画相交直线AB,CD的不同位置关系(方向差异).
在教学过程中,引导学生充分用语言表述概念和说理过程,针对图形解释陈述,说明推理步骤. 这是应用了演绎推理中“用语言表达陈述,基于任务与空间结合构建推理步骤,结合空间视觉,用语言符号表达推理过程”的认知神经学原理.
(5)特殊化.
首先,动态展示图9中直线CD绕着点O的旋转过程,让学生基于水平方向和纵向知觉的敏感性发现垂直这一特殊情况,给出两条直线垂直的相关定义,研究其性质(相交形成的四个角相等). 其次,引导学生画垂线,通过画垂线活动的归纳,结合空间视觉想象获得垂线的唯一性基本事实. 再次,引导学生进一步研究怎样刻画直线外一点与直线的位置关系,基于两点之间距离的动态变化,通过找代表引入刻画点与直线位置关系的量化工具——点到直线的距离. 最后,引导学生用点到直线的距离的概念解决现实问题.
在完成相交线的研究后,配置一节习题课,帮助学生理解相交线、垂线、邻补角、对顶角的概念,用邻补角互补、对顶角相等及垂线的相关知识进行推理计算,解决实际问题. 例如,间接测量角度,应用距离研究问题等. 相交线的教学设计应用了“数学演绎证明发展基于知觉运动经验的原理”和融合直观与逻辑的教学策略.
3. 分步实施2——用基准直线研究两条直线的位置关系
(1)提出问题.
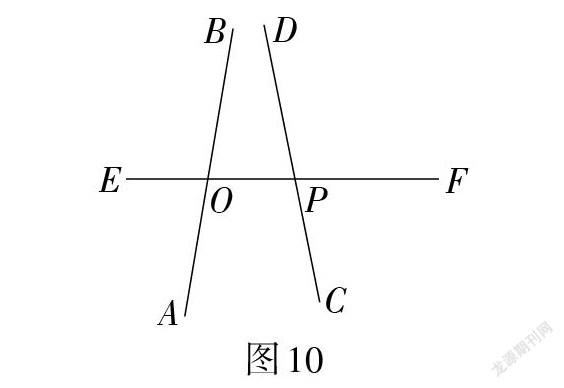
如图10,直线AB固定,旋转直线CD,怎样刻画直线AB,CD的位置关系(即方向关系)?
(2)分析问题.
直线AB和直线CD的方向都可以以直线EF的方向为基准,借助角来刻画. 例如,可以借助∠BOF和∠DPF分别刻画直线AB和直线CD的方向. 进一步引导学生思考:怎样用角的关系刻画直线AB和直线CD的方向关系?显然,需要研究以点O为顶点的角和以P为顶点的角之间的关系.
(3)解决问题.
类似于两条直线相交,研究以点O为顶点及以点P为顶点的角之间的位置关系. 这样,引入同位角、内错角、同旁内角的概念就水到渠成了. 当然,还有其他位置关系,只要重点学习这三种基本位置关系的角即可. 要注意的是,“三线八角”中学生学习的难点是对这些角的空间位置关系的辨别,以找“截线(两角的一边所在的共同直线)”为重点,需要通过操作、借助手势等进行强化训练.
(4)特殊化——研究平行线.
① 建构图形.
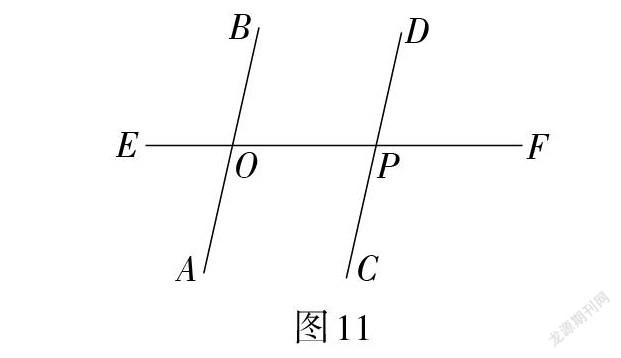
通过动画展示直线CD的旋转变化过程,引导学生观察图10中直线AB与直线CD的特殊情况——同向(如图11). 指出这是本单元研究的重点. 观察同向直线的特点——没有公共点,在此直观经验的基础上结合平面上两条直线位置关系的分类,给出平行线的定义:同一平面内不相交(没有公共点)的直线叫做平行线.
通过直观观察和想象,确认基本事实:过直线外一点有且只有一条直线与已知直线平行.
② 提出问题.
根据定义,无法检验两条直线是否平行. 提出问题:需要给出可操作的判断两条直线平行的方法.
③ 分析问题.
从哪里寻找可操作的判断方法?由于方向相同的两条不同直线从直观上看没有公共点. 因此,从刻画直线方向的角的关系上寻找可操作的判断准则. 通过动态展示直线CD绕点P的旋转过程,可以发现同位角相等时意味着直线AB和直线CD同向,此时这两条直线平行. 通过直观观察和想象概括出“两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行”. 为了深化学生的直观理解,可以引导学生开展作平行线的活动(无约束画平行线,过直线外一点画已知直线的平行线),可以用平推法画平行线,也可以用其他方法画平行线(教学实践中,学生更多采用的是画垂线构造90°的同位角的方法). 这两种画图方法的依据都是上述基本事实.
④ 解决问题.
有了上述基本事实,可以结合图11中的“三线八角”,思考是否能用内错角和同旁内角找到判定平行线的准则,并引导学生通过演绎推理得到“内错角相等,两直线平行”“同旁内角互补,两直线平行”.
(5)拓展问题——研究平行线的性质.
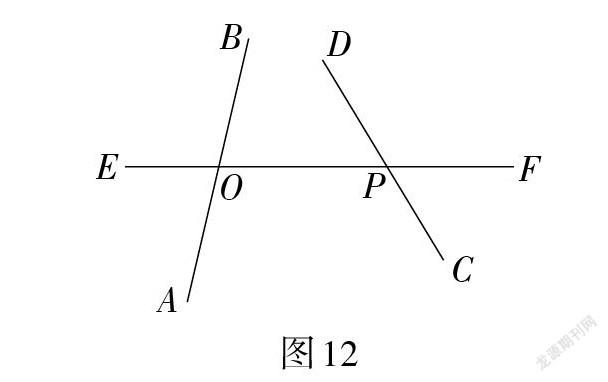
有了判定两条直线平行的方法,还要进一步研究判定两条直线不平行(相交)的方法. 引导学生结合图11思考:在同位角存在什么关系的情况下,直线AB和直线CD不平行(相交)?再次基于圖11展示直线CD的旋转动画,得到图12. 学生根据图形可以直观判断:两条直线被第三条直线所截,如果同位角不相等,那么这两条直线就不平行(相交). 进一步思考:能把这个命题中的“不”字去掉并进行改写吗?事实上,这一陈述的另一种表达方式是:如果两条直线平行,那么同位角不能不相等,即“两条直线平行,同位角相等”. 学生没有见过这种逆否命题的表述转换,需要举一些生活中的例子帮助理解,也可以让学生测量平行线被第三条直线截得的同位角,考察其大小关系,在两条直线平行的前提下,变化截线的位置,通过测量发现同位角相等,并通过归纳进行验证,还可以介绍反证法证明的过程.
有了这一平行线的同位角性质,可以引导学生类比平行线判定中的推理,通过推理得到平行线内错角和同旁内角的有关性质. 事实上,定义是刻画数学对象的充分必要条件,判定是刻画数学对象的充分条件,性质是刻画数学对象的必要条件. 性质越多越容易判断一个对象“不是什么”,而判定的条件越少越容易判断这个对象是“是什么”. 图形的一条性质定理如果其逆命题为真,它也可以作为判定定理,于是得到了这类图形的一个等价定义. 这就是为什么对于特殊的图形和图形关系都重视其性质定理逆命题的研究,得到判定的价值所在. 由于平行线判定的逆命题也真,所以这三个判定是判断两条直线平行的充分必要条件,这样我们就有了判断两条直线是否平行的正反两个方面可操作的方法,这就意味着我们完全把握了平面上两条直线的位置关系.
由于平行线的定义、性质、判定逻辑联系紧密,前后连贯、逻辑一致,这为进行研究性单元整体教学提供了良好的课程资源,通过这种教学,可以帮助学生体会直观与推理的关系,以及推理在建立命题之间联系、组织局部逻辑体系中的作用. 上述平行线的整体教学用两节联排课实施.
学生空间观念、几何直观和逻辑推理能力的发展离不开训练,但要整合课堂内外整体审视思维训练,课堂中的直观感知、操作确认、推理论证是训练的主平台,课外训练是课内训练的延续、拓展和补充. 平行线的研究可以配两节习题课:第一节课单独应用平行线的判定或性质进行推理计算;第二节课综合运用平行线的判定和性质进行推理计算,解决简单的问题.
4. 基于平行线研究结果的逻辑整理,进行“命题与证明”的教学
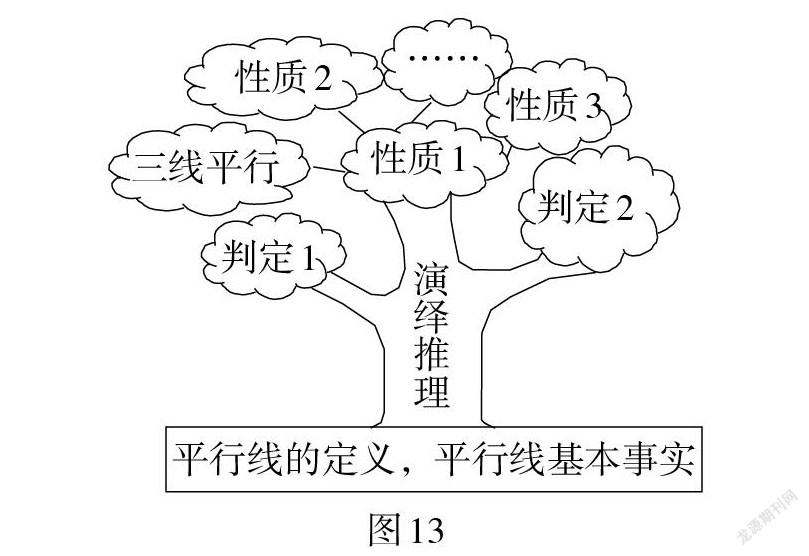
在“命题与证明”内容的教学中,以相交线、平行线研究成果的逻辑整理为主线,介绍命题、定义、证明的相关概念,结合具体推理过程中的命题(如证明“内错角相等,两条直线平行”)让学生体会命题是数学陈述的语言表达工具,推理是以“论证命题”为桥梁沟通前提命题和结论命题,知道命题的基本结构是“题设 + 结论”,命题的分类(真命题、假命题;真命题中的定义、基本事实、定理等). 在此基础上,设计习题课,让学生对平行线的相关命题进行局部逻辑整理,明确哪些是不需要证明的基本事实和定义,哪些是需要证明的定理;明确知识生成的次序结构,形成如图13所示的知识树,让学生体会数学知识大厦是怎样依据逻辑逐步建立起来的,促进学生的逻辑推理能力向更高水平发展.
5. 整体复习,建构知识体系
在完成本单元的教学后,需要进行回顾整理,建立知识之间的联系,在相互联系中深化对知识的理解,建构知识体系,总结研究过程中的数学思想方法及数学研究活动经验. 可以先根据目录整体粗略回顾研究主线,如图14所示.
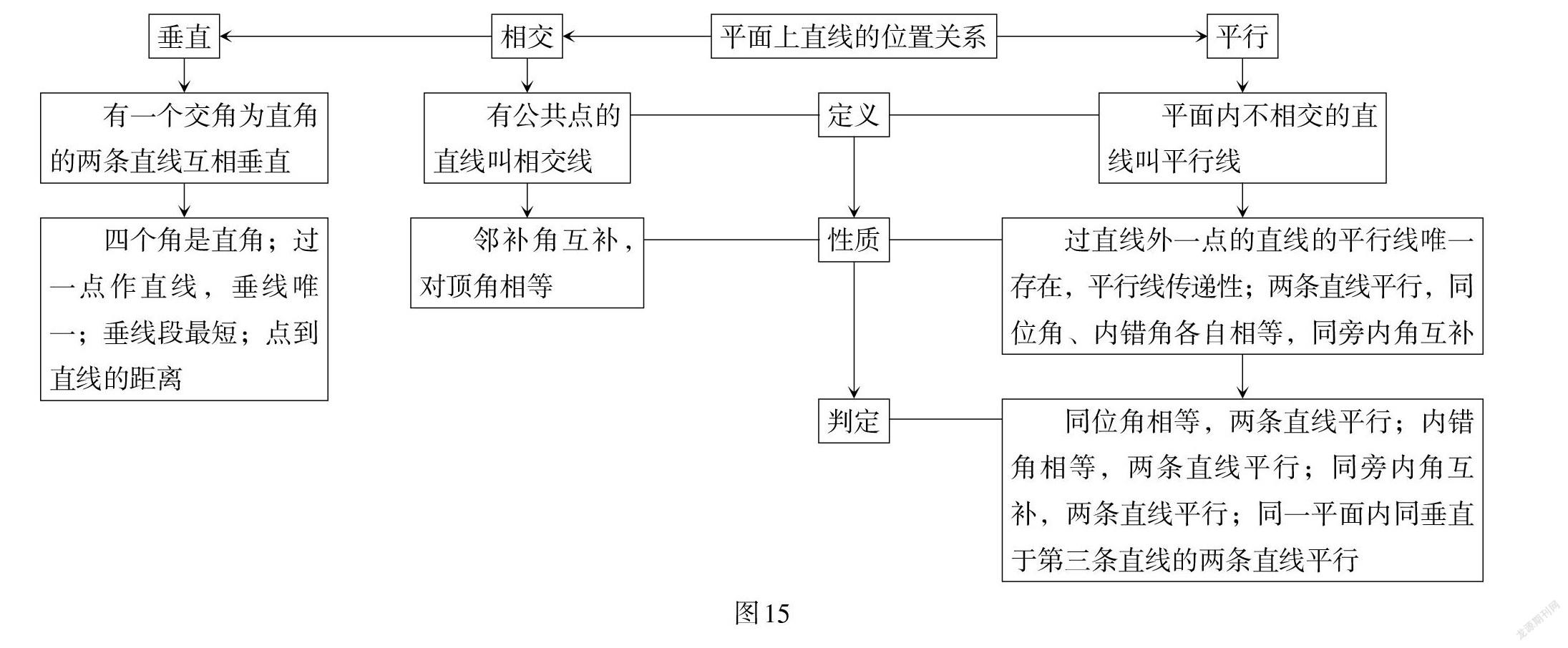
再进一步回顾研究得到的结果,形成知识结构图,如图15所示.
在此基础上,进一步总结相交线与平行线的研究思路、研究内容和研究方法.
(1)研究思路.
相交线:引入—定义—性质—特例(垂线);
平行线:定义—判定、性质.
(2)研究内容.
用角及其关系量化刻画平面上两条直线的位置关系(方向关系).
(3)研究方法.
画出图形、直观观察、动态想象—提出猜想—验证猜想(操作确认,推理证明).
单元复习课中,应该先引导学生进行认知重构,整理知识结构,深化知识理解,总结思想方法和活动经验,形成图形及图形关系研究的一般观念,便于迁移到新的图形与图形关系的研究中. 当然,单元复习中还需要进行知识、思想方法的理解和应用,通过有层次的训练巩固知识、发展能力.
6. 设计研究性作业与习题课
学生空间观念、几何直观和推理能力的发展,研究几何图形关系的经验积累,需要综合运用知识、思想方法和活动经验解决问题的活动,可以通过研究性作业及习题课来实现. 研究性习题课教学设计的关键是选择适当的研究主题和研究材料. 例如,可以用以下问题和材料引导学生抽象几何图形关系并进行主题研究活动.
主题作业1:设计潜望镜.
用两面平面镜,试着调整平面镜的位置.
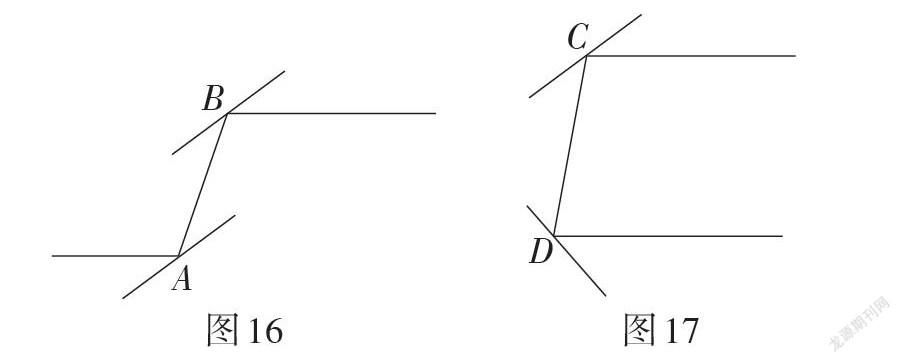
(1)设计简易的前视潜望镜装置(如图16);
(2)设计简易的后视潜望镜装置(如图17).
要求:网上搜索平面镜反射原理,明确两个平面镜的位置关系,并说明理由.
答案:(1)两个平面镜互相平行;
(2)两个平面镜互相垂直.
主题作业2:测量城墙拐角.
如图18所示的两面古城墙,如何测量其拐角?试设计测量方案,并说明理由.
引导学生设计测量方案,并用推理的方法说明理由(有多种测量方法,如用对顶角相等,用平行线的判定和性质等).
五、结束语
运用研究性整体教学策略设计学生的主题研究活动,既可以激发学生学习数学的兴趣,促进积极情绪的形成和发展,又可以发展学生大脑的元认知策略,形成可以远迁移的几何研究的一般观念;基于空间知觉运动经验,借助语言符号开展融合直观与逻辑的研究活动,可以充分应用大脑的空间视觉的神经机制促进学生的几何学习,促进空间与数量、空间与时间、空间与运动、空间数量与语言加工的大脑功能融合发展,促进学生空间观念、几何直观和推理能力的发展;通过分层次的分散与集中相结合的训练,可以帮助学生巩固知识,形成思想方法;通过主题化、研究性跨学科问题解决,可以促进学生数学学科核心素养和“四能”的发展. 这是基于教育神经科学视野的几何研究性单元整体教学的主要策略. 通过案例设计研究,把“融合直观与逻辑的研究性单元整体教学”运用于教学实践,收集证据,分析教学效果,这是今后进一步研究的重点.
参考文献:
[1]周加仙. 教育神经科学视角的知识创造与知识判断标准[J]. 教育发展研究,2018,38(24):48-53,72.
[2]AMALRIC M,DEHAENE S. A distinct cortical network for mathematical knowledge in the human brain[J]. Neuroimage,2019(189):19-31.
[3]楊雅琳,杨伟星,张明亮,等. 从数量表征到数表征:具身认知视角下的人类数能力获得[J]. 心理科学,2018,41(1):91-97.
[4]ZHOU X L,LI M Y, LI L N,et al. The semantic system is involved in mathematical problem solving[J]. Neuroimage,2017(166):360-370.
[5]KIM H. Default network activation during episodic and semantic memory retrieval:A selective meta-analytic comparison[J]. Neuropsychologia,2016(80):35-46.
[6]TOOMARIAN E Y,HUBBARD E M. On the genesis of spatial-numerical associations:Evolutionary and cultural factors co-construct the mental number line[J]. Neuroscience and Biobehavioral Reviews,2018(90):184-199.
[7]KRAVITZ D J,SALEEM K S,BAKER C I,et al. A new neural framework for visuospatial processing[J]. Nature Reviews Neuroscience,2011,12(4):217-230.
[8]JIA X Q,LIANG P P ,SHI L,et al. Prefrontal and parietal activity is modulated by the rule complexity of inductive reasoning and can be predicted by a cognitive model[J]. Neuropsychologia,2015(66):67-74.
[9]Holyoak K J,Morrison R G. The Cambridge Handbook of Thinking and Reasoning[M]. Cambridge:Cambridge University Press,2015.
[10]RODRIGUEZ-MORENO D,HIRSCH J. The dynamics of deductive reasoning:An fMRI investigation[J]. Neuropsychologia,2009,47(4):949-961.
[11]Prado J. The relationship between deductive reasoning and the syntax of language in Broca’s area:A review of the neuroimaging literature[J]. Annee psychologique,2018,118(3):289-315.
[12]刘志雅. 演绎推理认知神经研究[J]. 华南师范大学学报(社会科学版),2011(4):120-125.
[13]ANDERSON J R,LEE H S,FINCHAM J M. Discovering the structure of mathematical problem solving[J]. NeuroImage,2014(97):163-177.
[14]ANDERSON J R,BETTS S,FERRIS J L,et al. Cognitive and metacognitive activity in mathematical problem solving:prefrontal and parietal patterns[J]. Cognitive,Affective and Behavioral Neuroscience,2011,11(1):52-67.
[15]BRYANT R A,ANDREW E,KORGAONKAR M S. Distinct neural mechanisms of emotional processing in prolonged grief disorder[J]. Psychological medicine,2020:1-9.
[16]吳增生. 教育神经科学视野下的初中几何教学策略创新[J]. 教育生物学杂志,2021,9(3):249-256.
[17]中华人民共和国教育部制定. 义务教育数学课程标准(2011年版)[M]. 北京:北京师范大学出版社,2012.
[18]HUBEL D H,WIESEL T N. Receptive fields,binocular interaction and functional architecture in the cat’s visual cortex[J]. The Journal of Physiology,1962,160(1):106-154.
[19]MONTI M M,OSHERSON D N. Logic,language and the brain[J]. Brain research,2012(1428):33-42.
[20]FRENCH R L,DEANGELIS G C. Multisensory neural processing:from cue integration to causal inference[J]. Current Opinion in Physiology,2020(16): 8-13.

