指数函数与对数函数常见典型考题赏析

■吕利青 张文伟

指数函数与对数函数是高中数学的主要内容,也是高考的常考内容。同学们要理解分数指数幂的概念与运算性质,掌握指数函数的概念、图像与性质;理解对数的概念与运算性质,掌握对数函数的概念、图像和性质。要学会用指数函数和对数函数的性质解决某些简单的实际问题,要掌握函数的零点以及函数模型的应用。

题型1:指数幂中的条件求值问题

求解此类问题应注意分析已知条件,通过将已知条件中的式子变形(如平方、因式分解等),寻找已知式和待求式的关系,可考虑使用整体代换法。

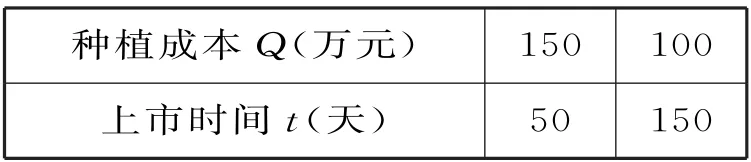
例1 已知x+y=12,xy=9,且x

题型2:指数函数的概念问题

解决指数函数问题,要注意底数大于0且不等于1这一条件。已知指数函数求参数值的方法:依据指数函数形式列方程或不等式,通过解方程或不等式获解。

例2 若y=(a2-3a+3)ax是指数函数,则( )。

A.a=1或a=2 B.a=1

C.a=2 D.a>0且a≠1

题型3:指数函数的图像问题

解答与指数函数有关的图像问题,只需利用指数函数的图像作平移变换或对称变换即可,值得注意的是作图前要探究函数的定义域和值域,掌握图像的大致趋势。利用熟悉的函数图像作图,主要运用图像的平移、对称等变换,但平移要注意平移的方向和平移的单位。

(1)f(x-1)的图像:将函数f(x)的图像向右平移1个单位长度得f(x-1)的图像(图略)。

(2)-f(x)的图像:由f(x)的图像关于x轴对称得-f(x)的图像(图略)。

(3)f(-x)的图像:由f(x)的图像关于y轴对称得f(-x)的图像(图略)。

由图可知,此函数有三个重要性质:①对称性,图像的对称轴为直线x=1;②单调性,在(-∞,1]上单调递减,在[1,+∞)上单调递增;③函数的值域为[1,+∞)。

题型4:指数型函数的定义域和值域问题

形如y=af(x)的函数的定义域就是f(x)的定义域。求形如y=af(x)的函数值域:先求出f(x)的值域,再由函数的单调性可求出af(x)的值域,若a的取值范围不确定,则需对a进行分类讨论。求形如y=f(ax)的函数值域:先求出u=ax的值域,再结合y=f(u),求出y=f(ax)的值域。

题型5:对数函数的概念问题

在对数函数的解析式y=logax中,logax的系数必须为1,真数必须为x,底数a必须是大于0且不等于1的常数。

例5 指出下列函数中,哪些是对数函数。

提示:形如y=logax(a>0,且a≠1)的函数是对数函数。应选A。

题型6:与对数函数有关的定义域问题

求与对数函数有关的定义域问题应遵循的原则:(1)分母不能为0;(2)根指数为偶数时,被开方数非负;(3)对数的真数大于0,底数大于0且不等于1。

例6 求下列函数的定义域。函数的定义域是{x|x>1,且x≠2}。

(2)要使此函数有意义,需满足16-4x>0,解得x<2,所以此函数的定义域是{x|x<2}。

题型7:对数型函数的图像问题

若函数y=m+logaf(x)(a>0,且a≠1)的图像过定点,则令f(x)=1,即得定点为(x,m)。给出函数解析式判断函数的图像的方法:(排除法)首先,考虑函数对应的基本初等函数是哪一种;其次,找出函数图像的特殊点,判断函数的基本性质(定义域、单调性以及奇偶性);最后,综合上述几个方面将图像选出。根据对数函数图像判断底数大小的方法:作直线y=1与所给图像相交,交点的横坐标即为各个底数,根据在第一象限内,自左向右,图像对应的对数函数的底数逐渐变大,即可比较底数的大小。

例7 在同一直角坐标系中,函数y=2-x与y=log2x的图像是( )。单调递减,函数y=log2x过定点(1,0)且单调递增。应选A。

跟踪训练7:已知函数y=loga(x+b)(a>0,且a≠1)的图像,如图3所示。

(1)求实数a与b的值。

(2)函数y=loga(x+b)与y=logax的图像有何关系?

提示:(1)由图可知,图像过点(-3,0),(0,2),所以0=loga(-3+b),2=logab,解得a=2,b=4。

(2)函数y=loga(x+4)的图像可以由y=logax的图像向左平移4个单位得到。

题型8:不同函数增长的差异问题

不同函数模型的选取标准:(1)线性函数增长模型适合于描述增长速度不变的变化规律;(2)指数函数增长模型适合于描述增长速度急剧变化的规律;(3)对数函数增长模型适合于描述增长速度平缓变化的规律;(4)幂函数增长模型适合于描述增长速度一般的变化规律。

例8 某学校为了实现60万元的生源利润目标,准备制定一个激励招生人员的奖励方案:在生源利润达到5万元时,按生源利润进行奖励,且奖金y(单位:万元)随生源利润x(单位:万元)的增加而增加,但奖金总数不超过3 万元,同时奖金不超过利润的20%。现有三个奖励模型,即y=0.2x,y=log5x,y=1.02x,其中哪个模型符合该校的要求?

解:作出函数y=3,y=0.2x,y=log5x,y=1.02x的图像(如图4所示)。

图4

由图可知,在区间[5,60]上,y=0.2x,y=1.02x的图像都有一部分在直线y=3的上方,只有y=log5x的图像始终在y=3和y=0.2x的下方,这说明只有按模型y=log5x进行奖励才符合学校的要求。

跟踪训练8:三个变量y1,y2,y3,随着自变量x的变化情况如表1所示。

x 1 3 5 7 9 11___y1 5 135 625 1715 3645 6655_y2 5 29 245 2189 19685 177149 y3 5 6.1 6.61 6.985 7.2 7.4___

则关于x分别呈对数函数,指数函数,幂函数变化的变量依次为( )。

A.y1,y2,y3B.y2,y1,y3

C.y3,y2,y1D.y1,y3,y2

提示:由指数函数,对数函数,幂函数三种不同函数模型的增长规律比较可知,对数函数的增长速度越来越慢,变量y3随x的变化符合此规律;指数函数的增长速度成倍增长,y2随x的变化符合此规律;幂函数的增长速度介于指数函数与对数函数之间,y1随x的变化符合此规律。应选C。

题型9:用二分法求方程的近似解问题

二分法就是通过不断地将所选区间一分为二,使区间的两个端点逐步逼近零点,直至找到零点附近足够小的区间,根据所要求的精确度,用此区间的某个数值近似地表示真正的零点。二分法求方程近似解的适用范围:在包含方程解的一个区间上,函数图像是连续的,且两端点函数值异号。求函数零点的近似值时,若要求的精确度不同,则得到的结果也不相同。

例9 在用二分法求函数f(x)零点近似值时,第一次所取的区间是[-2,4],则第三次所取的区间可能是( )。

解:由于第一次所取的区间为[-2,4],所以第二次所取区间为[-2,1]或[1,4],第

跟踪训练9:用二分法求方程ln(2x+6)+2=3x的根的近似值时,令f(x)=ln(2x+6)+2-3x,并用计算器得到表2。

x 1.00 1.25 1.375 1.50__f(x)1.0794 0.1918 -0.3604 -0.9989

由表中的数据可得方程ln(2x+6)+2=3x的一个近似解(精确度为0.1)为( )。

A.1.125 B.1.3125

C.1.4375 D.1.46875

提示:由f(1.25)·f(1.375)<0,再根据二分法知函数f(x)的零点在区间(1.25,1.375)内,但区间(1.25,1.375)的长度为0.125>0.1,因此需要取(1.25,1.375)的中点1.3125,则两个区间(1.25,1.3125)和(1.3125,1.375)中必有一个满足区间端点的函数值符号相异。因为区间的长度为0.0625<0.1,因此1.3125 是一个近似解。应选B。

题型10:判断函数零点所在的区间问题

判断一个函数是否有零点,要看函数f(x)在区间[a,b]上的图像是否连续,若连续,且f(a)·f(b)<0,则函数y=f(x)在区间(a,b)内必有零点。对于连续函数f(x),若存在f(a)·f(b)<0,则f(x)在区间(a,b)内有零点,若只有一个零点,则称此零点为变号零点,反过来,若f(a)与f(b)不变号,而是同号,即不满足f(a)·f(b)<0,也不能说函数在(a,b)内无零点,如函数f(x)=x2,f(-1)·f(1)=1>0,但0是函数f(x)的零点。

例10 若a

A.(a,b)和(b,c)内

B.(-∞,a)和(a,b)内

C.(b,c)和(c,+∞)内

D.(-∞,a)和(c,+∞)内

解:由f(x)=(x-a)(x-b)+(x-b)·(x-c)+(x-c)(x-a),可得f(a)=(ab)(a-c),f(b)=(b-c)(b-a),f(c)=(c-a)(c-b)。由a0,f(b)<0,f(c)>0,可知f(x)的两个零点分别位于区间(a,b)和(b,c)内。应选A。

跟踪训练10:根据表3中的数据,可以判断方程ex-x-2=0的一个解所在的最小区间为_____。

x -1 0 1 2 3__ex 0.37 1 2.72 7.39 20.09 x+2 1 2 3 4 5__

提示:解题的关键是判断ex与x+2 的差的符号。构造函数f(x)=ex-x-2,将求方程ex-x-2=0的解所在的区间转化为求函数的零点问题。由表中数据知f(-1)=0.37-1=-0.63,f(0)=1-2=-1,f(1)=2.72-3=-0.28,f(2)=7.39-4=3.39,

f(3)=20.09-5=15.09。由此可得f(1)·f(2)<0,可知此方程一个解所在的最小区间为(1,2)。

题型11:判断函数零点的个数问题

判断函数零点个数的方法:(1)直接求出函数的零点;(2)结合函数图像进行判断;(3)借助函数的单调性进行判断,若函数f(x)在区间[a,b]上的图像是一条连续不断的曲线,且在区间(a,b)上单调,满足f(a)·f(b)<0,则函数f(x)在区间(a,b)上有且仅有一个零点。

A.0 B.1

C.2 D.3

解:(方法1)方程x+2=0(x<0)的根为x=-2,方程x2-1=0(x>0)的根为x=1,所以函数f(x)有2个零点。应选C。

图5

由图可知,f(x)的图像与x轴有2个交点,即函数f(x)有2个零点。应选C。

跟踪训练11:已知0

A.1 B.2

C.3 D.4

提示:函数y=a|x|-|logax|(0

的零点个数即方程a|x|=|logax|(0

由图可知,函数f(x)=a|x|(0

题型12:函数零点的应用问题

函数零点的应用主要是利用函数零点的相关知识求参数的值或参数的取值范围。解答这类问题,可设出方程对应的函数,根据函数的零点所在的区间分析区间端点函数值的符号,建立方程或不等式求解,当函数解析式中含有参数时,要注意分类讨论。

例12 已知关于x的方程x2-2ax+4=0,在下列条件下,求实数a的取值范围。

(1)一个根大于1,一个根小于1。

(2)一个根在(0,1)内,另一个根在(6,8)内。

题型13:函数模型的应用及数学建模问题

两种常用的函数模型:指数型函数模型,即y=a·bx+c(a,b,c为常数,b>0且b≠1,a≠0);对数型函数模型,即y=alogbx+c(a,b,c为常数,b>0 且b≠1,a≠0)。用函数建立数学模型解决实际问题的基本过程如下:

例13 设在海拔xm 处的大气压强是yPa,y与x之间的函数关系式为y=cekx,其中c,k为常量。已知某地某天海平面上的大气压为1.01×105Pa,1000m 高空的大气压为0.9×105Pa,求600m 高空的大气压强(结果保留3位有效数字)。

解:将x=0,y=1.01×105和x=1000,y=0.9×105分别代入函数关系式y=cekx中

跟踪训练13:某蔬菜基地种植青瓜,由历年市场行情得知,从4 月1 日起的300 天内,青瓜的种植成本Q(万元)与上市时间t(天)的关系如表4所示。

种植成本Q(万元) 150 100_上市时间t(天) 50 150_

模拟函数可以选用二次函数Q=a(t-150)2+b(a,b为常数,且a≠0),或一次函数Q=kt+m(k,m为常数,且k≠0)。已知种植成本Q=112.5(万元)时,上市时间t=200(天),则用以上哪个函数作为模拟函数较好?请说明理由。