例析指数函数的图像与性质问题

■欧阳亮

指数函数是高中数学的重要内容,也是高考的考查重点。下面举例分析指数函数的图像与性质的常见题型,供大家学习与提高。

题型1:根据函数判断图像

例1 已知1>n>m>0,则指数函数:①y=mx,②y=nx的图像为( )。

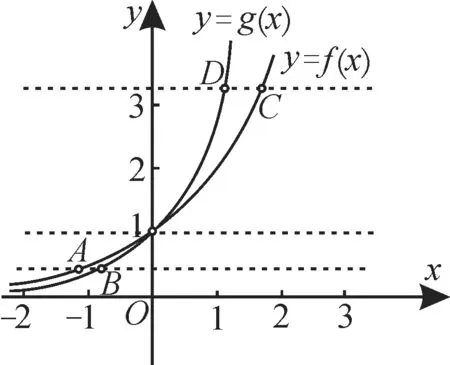
解:由0

评注:识别函数图像可从以下几个方面入手:(1)从函数的定义域,判断图像的左右位置,从函数的值域,判断图像的上下位置;(2)从函数的单调性,判断图像的变化趋势;(3)从函数的奇偶性,判断图像的对称性;(4)从函数的周期性,判断图像的循环往复;(5)从函数的特征点,排除不合要求的图像。

题型2:函数的图像恒过定点

例2 函数f(x)=ax-2021+2022(a>0,且a≠1)恒过的定点为____。

解:函数y=ax(a>0,且a≠1)的图像恒过定点(0,1)。令x-2021=0 得x=2021,所以f(2021)=1+2022=2023。故函数f(x)=ax-2021+2022(a>0,且a≠1)恒过定点为(2021,2023)。

评注:本题也可令a=2和a=4,得到两个关于x,y的方程,解出方程组可得图像经过的定点坐标。

题型3:求参数的取值范围

例 3 若 分 段 函 数f(x)=

解:当a>1时,f(x)在(-∞,-1)上是增函数,在[-1,+∞)上是减函数,则函数f(x)在R 上不是单调函数,可知a>1 不合题意;当0

评注:对数函数的底数中含有参数,解题时要注意分类讨论,且分类要全面,做到不重不漏。

题型4:利用图像比较大小

例4 已知实数a,b满足等式2a=3b,给出下列五个关系式:①0

解:在同一直角坐标系中作出函数f(x)=2x,g(x)=3x的图像,如图1所示。

图1

由图可知,当直线AB位于y=1 下方时,交点A,B的函数值相等(2a=3b),但a

评注:比较指数式的大小的两种方法:当底数相同时,运用指数函数的单调性求解;当底数不同时,利用一个中间量做比较进行求解,或借助于同一坐标系中的图像求解。

题型5:指数函数图像的平移变换

例5 为了得到函数y=ex-3+1 的图像,只需把函数y=ex的图像上所有的点( )。

A.向左平移3个单位长度,再向上平移1个单位长度

B.向右平移3个单位长度,再向上平移1个单位长度

C.向左平移3个单位长度,再向下平移1个单位长度

D.向右平移3个单位长度,再向下平移1个单位长度

解:函数y=ex的图像向右平移3 个单位长度到得函数y=ex-3的图像,再向上平移1个单位长度得到函数y=ex-3+1的图像。应选A。

评注:把y=f(x)的图像向左平移a(a>0)个单位长度得到函数y=f(x+a)的图像;把y=f(x)的图像向右平移a(a>0)个单位长度得到函数y=f(x-a)的图像;把y=f(x)的图像向上平移a(a>0)个单位长度得到函数y=f(x)+a的图像;把y=f(x)的图像向下平移a(a>0)个单位长度得到函数y=f(x)-a的图像。

题型6:求函数的单调区间的增区间为(-∞,1],所以函数f(x)的减区间为(-∞,1]。

评注:求解与指数函数有关的复合函数问题,要明确复合函数的构成,涉及值域、单调区间、最值等问题时,都要借助“同增异减”的法则进行判断。

1.若函数y=ax+b-1(a>0,且a≠1)的图像经过第二、三、四象限,则一定有( )。

A.00

B.a>1,且b>0

C.0

D.a>1,且b<0

图2