基于COVID-19传染病SIR模型的稳定性分析
成红胜, 成 诚
(1.盐城师范学院 信息工程学院, 江苏 盐城 224001; 2.江苏师范大学 数学与统计学院, 江苏 徐州 221116)
0 引言
2020年年初,一种类似于“非典”的新型冠状病毒肺炎在武汉被发现并迅速传播开来,这场疫情给全人类的生命健康造成了重大威胁.在全民抗击疫情的过程中,运用数学模型预测疫情的走势在防控疫情过程中发挥了重要的作用,为一线的医护人员提供了科学的理论指导和精准的预测.新冠疫情爆发已经过去一年多,世界各地陆续发现感染新冠病毒康复后复阳的病例.基于这种实际情况,研究一类具有饱和发生率和暂时免疫力的传染病SIR模型,得到平衡点的相关性质,有望从科学的角度研究传染病的传播机制.
长久以来,人们对于传染病模型的研究已经取得了一些显著的成果.Wen等学者研究了一类具有暂时免疫力的SIR模型[1]:
(1)
其中:S(t)的表示容易被传染该种疾病的总人数;I(t)表示已经被传染该种疾病的人数;R(t)表示因接种疫苗从而获得暂时免疫力的人数;μ表示由易感染变成感染者的速率.参数μ1、μ2、μ3均为非负常数,μ1表示易感染人群的死亡率;μ2表示感染者的死亡率;μ3表示从该种传染病康复者的死亡率.从生物学的角度来看,μ1 (2) 系统(2)中的初始条件表示如下: (3) (4) 分离变量可得 (5) 等式两边同时积分可得方程的解为 (6) 假设ξ表示感染者的平均寿命,可得概率函数为 (7) 其中的概率密度函数为 (8) 由此计算得到数学期望 (9) 因此系统(2)存在一个无病平衡点E0.通过计算E0处的Jacobi矩阵,得到特征方程为 (10) 求解得到三个特征值分别为 定理3 当R0<1且μ1=μ2=μ3时,系统(2)在E0(S0,0,0)处在全局的性质是渐近稳定的. 证明构造如下的Lyapunov函数: (11) 等式两端同时对时间t求导得 [S(t)+I(t)+R(t)-S0](μ-μ1S(t)-μ2I(t)-μ3R(t)) (12) 因为μ1=μ2=μ3,进一步简化式(12)得 [S(t)+I(t)+R(t)-S0](μS(0)-μ1S(t)-μ2I(t)= -μ1[S(t)+I(t)+R(t)-S0]2= -μ1[[S(t)-S0]+I(t)+R(t)]2 (13) 定理4 系统(2)存在一个地方病平衡点E*(S*,I*,R*),当R0>1时,系统(2)在E*处是局部性质渐近稳定的;当R0<1时,系统(2)在E*处是不稳定的. 证明证明方法与定理2的证明过程类似. 令系统(2)中等式左侧等于零,即可求得这个系统的地方病平衡点为E*(S*,I*,R*), 具体为 通过计算系统(2)在E*处的Jacobi矩阵,得到特征方程满足如下的形式: [λ2+p0(τ)+p1(τ)λ+q0(τ)eλτ](λ+μ3)=0 (14) 其中 显然,特征方程(14)有一个特征值-μ3且其实部为负数. 其余的特征值由以下方程所确定 λ2+p0(τ)+p1(τ)λ+q0(τ)eλτ (15) 下面将τ分为τ=0和τ>0两种情况进行讨论: 1) 当τ=0时,方程(15)可以写成: λ2+p1(0)λ+p0(0)+q0(0)=0 (16) 2) 当τ>0时,假设iω(ω>0)是方程(15)的一个解,将iω代入方程,分离实部和虚部得到如下的等价方程: (17) 将两个方程分别平方再相加,得到 (18) 其中 因此 综合1)和2)两种情况可知,当R0>1,对任意的τ≥0,地方病平衡点E*(S*,I*,R*)是局部渐近稳定的.当R0<1时,特征方程(15)必有一解是正数,故存在一个特征值的实部是正数,此时系统在E*处是不稳定的.证毕. 定理5当R0>1且μ1=μ2=μ3时,系统(2)在E*(S*,I*.R*)处是全局渐近稳定的. 证明构造Lyapunov泛函: (19) 等式两端同时对时间t求导得 [(S(t)-S*)+(I(t)-I*)+(R(t)-R*)](μ-μ1S(t)-βS(t)I(t)+ γI(t-τ)e-μ3τ+βS(t)I(t)-(μ2+γ)I(t)+γI(t)-μ3R(t)-γI(t-τ)e-μ3τ= [(S(t)-S*)+(I(t)-I*)+(R(t)-R*)](μ-μ1S(t)-μ2I(t)-μ3R(t)) 将μ1=μ2=μ3代入,上面的式子可以写成 [(S(t)-S*)+(I(t)-I*)+(R(t)-R*)][μ-μ(S(t)-S*)-μ(I(t)-I*)- μ(R(t)-R*)-μ(S*+I*+R*)]= [(S(t)-S*)+(I(t)-I*)+(R(t)-R*)][-μ(S(t)-S*)+(I(t)-I*)+ (R(t)-R*)]=-μ[(S(t)-S*)+(I(t)-I*)+(R(t)-R*)]2 1) 选取μ=0.3,α=2,β=0.1,γ=0.3,μ1=0.1,μ2=0.1,μ3=0.1,τ=15.计算得到R0=0.6<1,无病平衡点E0=(3,0,0).由定理3可知,系统(2)在E0处是全局渐近稳定的.通过Matlab进行数值模拟验证了该结论,结果如图1所示. 图1 无病平衡点的稳定性 图2 地方病平衡点的稳定性 基于疫情常态化的实际情况,研究了一种传染病SIR模型,这种模型具有饱和发生率和暂时免疫力. 通过分析特征函数和特征值,得到当R0<1时,无病平衡点E0在局部的性质是渐近稳定的,该传染病并不会传播,也不会变成一种流行病;当R0>1时,地方病平衡点E*在局部的性质是渐近稳定的,这种传染病最终会传播开来.通过建立Lyapunov函数,得到当R0<1且μ1=μ2=μ3时,无病平衡点E0在全局的性质是渐近稳定的;当R0>1且μ1=μ2=μ3时,地方病平衡点在全局的性质是渐近稳定的.最后通过Matlab进行模拟,验证所得到的结果.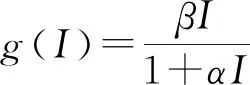
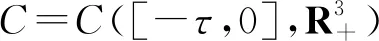
1 无病平衡点的稳定性
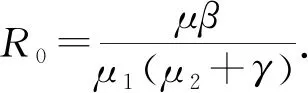
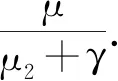
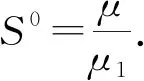
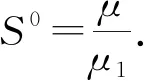
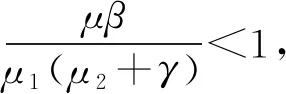

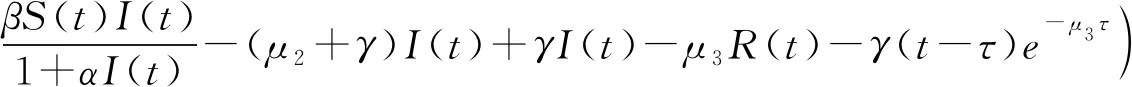

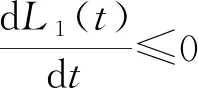
2 地方病平衡点的稳定性
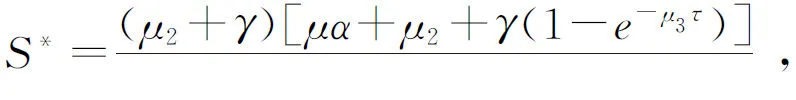
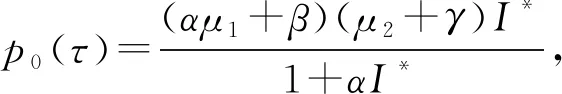
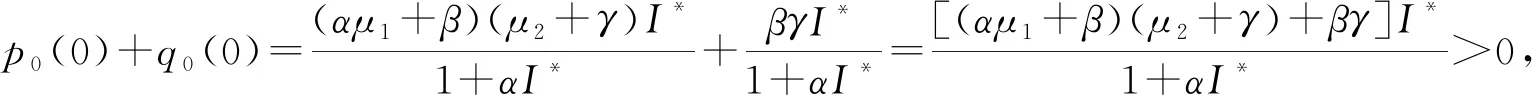
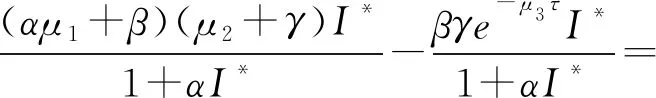
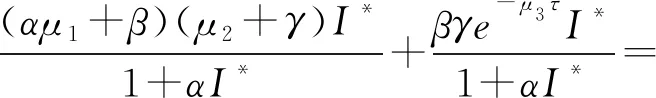
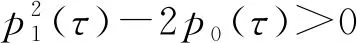
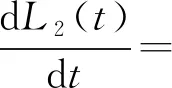
3 全局稳定性的数值模拟

4 结论

