具有Neumann边界条件的曲率方程解的估计
阿迪莱·玉苏普, 韩 菲
(新疆师范大学 数学科学学院, 新疆 乌鲁木齐 830017)
0 引言
Neumann边值问题是偏微分方程中的最重要的边值问题之一,给出解的先验估计是研究其解存在性的关键.
设Ω是Rn上的光滑有界区域,u是定义在Ω上的光滑函数,则u的图的平均曲率是
在n=1的情况下,相应的问题是曲线的曲率问题,也是微分几何和微分方程中关注的问题.
设u是定义在[0,1]上的光滑函数,则对应的曲线的曲率是
(1)
在偏微分方程中,对平均曲率流方程的研究比较广泛[1-3].对n≥2的情况,也有相关研究[4-5].与平均曲率有关的抛物方程
和
均可以描述曲面的一种演化.
2017年,唐榕[6]考虑了在Neumann边界条件下椭圆方程解的c0估计,c1估计,研究了如下方程
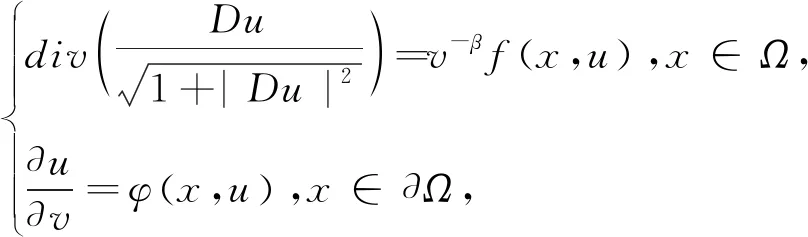
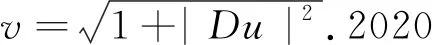
(2)
其中β≤3,且f(x,u)是定义在[0,1]×R上的光滑函数,得到了一类边值问题解的梯度估计,从而得到了相应的曲线曲率演化方程解的存在性定理.
受此启发,本文研究与式(1)有关的具有如下形式的一类抛物型方程
其中f(x,u,Du)是定义在[0,1]×R×Rn上的光滑函数且β≤3.
研究结果主要推广朱洁的抛物型方程中关于f只依赖于x,u时该方程解的c0估计,c1估计[7],即抛物型方程中关于f依赖于x,u,Du时该方程解的c0估计,c1估计.对于方程(2),当β=0和β=1时,方程的解的存在性、解的估计以及渐近性均已被证明[8-9].
1 主要结果
定理1 假设Ω=[0,1],β≤3,f是Ω×R×Rn上的光滑函数,设u(x,t)是下面方程的一个解
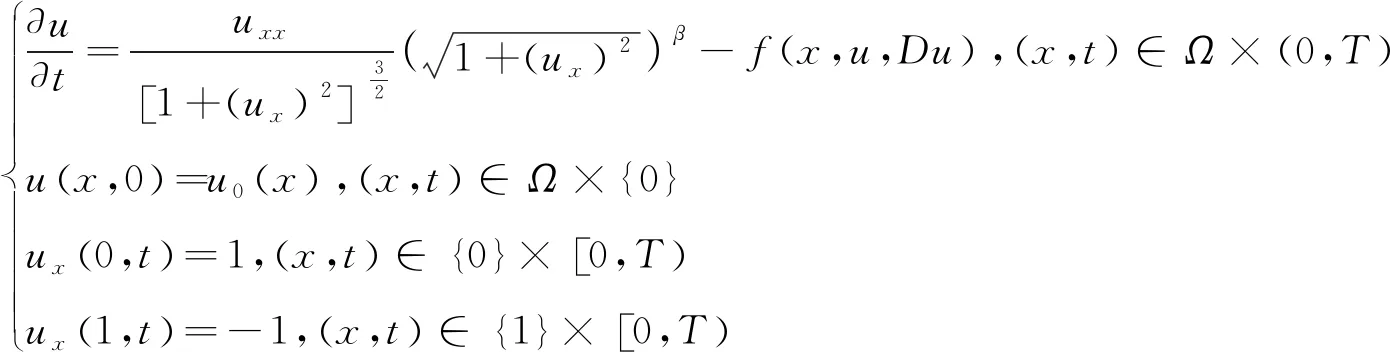
(3)
其中fz(x,z,p)≥-κ且κ≥0,对正常数L1,有
若t∈[0,T],则有
|ux(x,t)|≤C,

通过计算可得u和ut估计,结合定理1,易得到方程(3)的解的长时间存在性.
推论1 在定理1相同的条件下,抛物型方程
有光滑解u=u(x,t).
2 u的C0估计和ut估计
对于式(3),有

方程两边同时对t求导,得
(4)
而
(5)
将式(4)代入式(5),得
根据抛物型的强极值原理,知e-κtut的非负最大值和非正最小值均在边界取得,除非e-κtut在Ω内为常数.因此,假设e-κtut的非负最大值在(x0,t0)处取得,根据强极值原理,则(x0,t0)有下面3种情况:
(A1)t0=0;
(A2)t0>0且e-κtut在[0,1]×[0,t0]内为常数(等于ut(x,0));
(A3)t0>0且x0=0或x0=1;

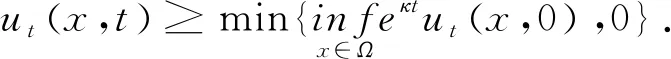
综上ut有界.
基于对ut的讨论,可以得到u的c0估计.事实上,由中值定理得
|u(x,t)-u0(x)|≤Cteκt,

3 u的C1估计
定理1的证明首先选取辅助函数Φ(x,t)=log(e-λt(ux)2)+g(x),其中g(x)=x2-x,λ定义在后面给出.设Φ(x,t)的最大值在点(x0,t0)处取得,其中x0∈[0,1].
下面分3种情形来讨论.
情形1:x0=0或x0=1,根据ux(0,t)=1,ux(1,t)=-1,知
情形2:t0=0,存在一个常数C=C(ux,0)>0,使得

根据极值原理,知

(6)
(7)
由式(3)知,ut=uxxvβ-3-f(x,u,Du).
因此
(8)
由式(6)知
(9)
将式(8)、(9)代入式(7)可得

其中
不妨假设ux充分大,否则u的C1估计已证.
由于β≤3,则β-3≤0,因此


则
令λ=2κ+10,由于ux充分大,则v与ux等价.由上式知
则

由于Φ(x,t)的最大值在点(x0,t0)处取得,故对任意的(x,t),有
Φ(x,t)≤Φ(x0,t0)=log((ux)2)(x0,t0)+g(x0)-λt0≤log (C1)2+g(x0)-λt0.
即
log((ux)2)+g(x)-λt≤log (C1)2+g(x0)-λt0.
故
log((ux)2)≤log(C1)2+g(x0)-g(x)+λ(t-t0)≤C,
其中C为与T有关的常数.综上所述,得到u的C1估计,从而完成了定理1的证明.

