归纳解析 直击中考

文／吴秀兰

各地中考对数据的集中趋势和离散程度的考查，分值虽然不高，却是必考的基础知识。下面，我们就近两年的相关中考题进行归纳、解析，希望对同学们有所帮助。

考点一 根据概念直接解题

此类问题考查的都是平均数、中位数、众数、方差等相关知识，熟知概念、理解意义是关键。

例1 （2020·江苏连云港）“红色小讲解员”演讲比赛中，7 位评委分别给出某位选手的原始评分。评定该选手成绩时，从7个原始评分中去掉一个最高分、一个最低分，得到5 个有效评分。5 个有效评分与7个原始评分相比，这两组数据一定不变的是（ ）。

A.中位数 B.众数

C.平均数 D.方差

【解析】从7 个原始评分中去掉1 个最高分和1 个最低分，得到5 个有效评分，5个有效评分与7 个原始评分相比，不变的是中位数。故选A。

变式 （2020·江苏镇江）在从小到大排列的五个数x，3，6，8，12 中再加入一个数，若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等，则x的值为________。

【解析】原来五个数的中位数是6，如果再加入一个数，变成了偶数个数，则中位数是中间两位数的平均数，由此可知加入的一个数是6，再根据平均数的公式得到关于x的方程，解方程即可求解。故答案为1。

考点二 从表格或图形中获取有用信息

在中考中，这类问题还会以表格或图形的方式给出。很多同学看到表格或图形就害怕，其实，只要认真审题，抓住相关量的关系，一样可以正确解题。

例2 （2021·江苏南京）某市在实施居民用水定额管理前，对居民生活用水情况进行了调查。通过简单随机抽样，获得了100 个家庭去年的月均用水量数据，将这组数据按从小到大的顺序排列，其中部分数据如表：

月均用水量/t 1.3_________________________________1.3…4.5________________________________4.5…6.4________________________________6.8…11_________________________________13__________________________________…25.6__________________________________28序号1 2____________________________…25 26___________________________…50 51___________________________…75 76___________________________…___________________________99 100____________________________

问题：求这组数据的中位数。已知这组数据的平均数为9.2t，你对它与中位数的差异有什么看法？

【解析】100 户家庭，就有100 个数据，根据中位数定义，取序号为50、51 两个数的平均值，就可以求出这组数据的中位数。从平均数与中位数的差异可知，大部分居民家庭去年的月均用水量小于平均数，有节约用水的观念，少数家庭用水比较浪费，所以我们要继续加强节水意识的培养。

例3 （2021·江苏泰州）近5 年，我省家电业的发展发生了新变化。以甲、乙、丙3 种家电为例，将这3 种家电2016～2020年的产量（单位：万台）绘制成如图所示的折线统计图，图中只标注了甲种家电产量的数据。

观察统计图回答下列问题：

（1）这5 年甲种家电产量的中位数为________万台；

（2）若将这5 年家电产量按年份绘制成5 个扇形统计图，每个统计图只反映该年这3 种家电产量占比，其中有一个扇形统计图的某种家电产量占比对应的圆心角大于180°，这个扇形统计图对应的年份是________年；（3）小明认为，某种家电产量的方差越小，说明该家电发展趋势越好。你同意他的观点吗？请结合图中乙、丙两种家电产量变化情况说明理由。

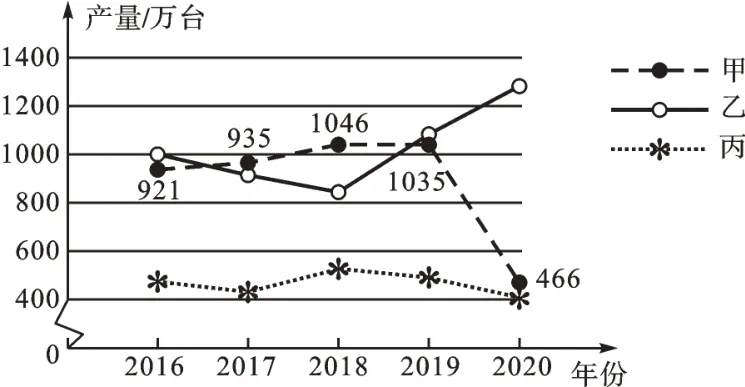
【解析】（1）这5 年甲种家电产量从小到大排列为：466，921，935，1035，1046，所以这5 年甲种家电产量的中位数为935 万台。故答案为935。

（2）由折线统计图可知，2020 年甲、丙两种家电产量和小于乙种家电产量，所以2020 年的扇形统计图的乙种家电产量占比对应的圆心角大于180°。故答案为2020。

（3）不同意小明的观点。理由：方差越小，说明数据越稳定。由折线统计图可知：丙种家电的方差较小，但丙种家电的产量低，而且是下降趋势；乙种家电的方差较大，但乙种家电的产量高，而且是上升趋势，说明发展趋势较好。因此，不同意小明的观点。