离散型和连续型改进Karnik-Mendel算法在高阶模糊系统降型中的关系研究*

陈 阳，王 涛

(辽宁工业大学理学院,辽宁 锦州 121001)

1 引言

当前，计算相对简单的区间二型模糊逻辑系统被成功应用于如智能控制[1]、预测[2]、永磁驱动[3]、故障诊断[4]和医疗系统[5]等诸多领域，它们是应用最广泛的一类模糊系统。尽管如此，自从广义二型模糊集的α-平面(或称z切片)[6 - 8]表达理论被几个不同研究小组提出，许多研究者的关注点逐渐从区间二型模糊逻辑系统逐渐转向了广义二型模糊逻辑系统[9]。广义二型模糊逻辑系统理论及其应用研究[10 - 13]在近年来得到了较充分的发展。由于广义二型模糊集的次隶属度介于[0,1],因此，它们可看成比区间二型模糊集更高阶的参数模型。随着设计自由度增加，广义二型模糊逻辑系统在处理不确定性上比区间二型模糊逻辑系统更具潜力。

一般来说，二型模糊逻辑系统是由模糊器、推理机[14]、规则库、降型器[15，16]和解模糊器5个模块组成。首先，在推理机的指导下，二型模糊输入集被转化成二型模糊输出集。接着，降型模块把二型模糊集映射成一型模糊集。最终解模糊化把一型模糊集变成明确输出。当前，最流行的降型算法是源于计算区间二型模糊集质心的KM(Karnik-Mendel)算法或改进EKM(Enhanced Karnik-Mendel)算法[17,18]，这类计算密集的算法具有保持不确定性在上下级隶属函数之间流动的优势。国内东南大学刘新旺教授等人[19]给出了EKM算法初始化的理论解释，以连续CEKM(Continuous EKM)算法为计算基准，扩展EKM为3种不同形式的加权WEKM(Weighted EKM)来计算出更准确的区间二型模糊集质心左端点。但是，WEKM算法的计算速度稍稍慢于EKM算法的。

本文扩展基准的CEKM算法计算来完成广义二型模糊逻辑系统质心降型，主要目标是提高离散EKM算法的计算精度。在研究中发现，不必对EKM算法进行加权，当适当改变系统质心输出广义二型模糊集主变量采样个数时，离散EKM算法计算出的广义二型模糊逻辑系统质心降型集和解模糊化值结果就可以精确地逼近CEKM算法。

2 广义二型模糊逻辑系统

(1)

其中，主变量x∈X，X为论域，次变量u∈[0,1]，式(1)为点-值表达式，其紧式如式(2)所示：

(2)

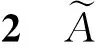
(3)

其中，x′表示任意主变量。

(4)

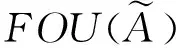
(5)

(6)

(7)

定义4Ae表示一个嵌入式一型模糊集，如式(8)所示:

Ae={(x,u(x)|∀x∈X,u∈Jx}

(8)

(9)

式(7)可重新被表达为：

(10)

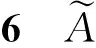
(11)

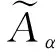
(12)

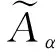
从推理结构的角度看，广义二型模糊逻辑可被分成2类：Mamdani型[10]和TSK(Takagi Sugeno Kang)型[20]。不失一般性，考虑一个Mamdani型广义二型模糊逻辑系统，假设它有n个输入x1∈X1,…,xn∈Xn和一个输出y∈Y，其中，xi表示第i个变量，Xi为xi的论域，Y为y的论域。系统由M模糊规则描述，其中第s条规则为：

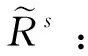
(13)

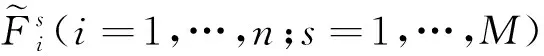
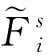
(14)

对于每条模糊规则，其相关的α水平下的激发区间如式(15)所示：

(15)

(16)

(17)

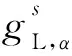
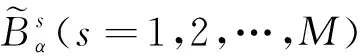
(18)

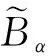
(19)

(20)

(21)

3 基于离散EKM和CEKM算法的广义二型模糊逻辑系统质心降型

对于离散EKM算法，聚合所有的α-平面YEKM,α(x′)构成一型模糊集YEKM，即:

(22)

步骤1取k=[N/2.4](最接近N/2.4的整数)且计算:

c′=a/b

步骤2找到k′∈[1,N-1]满足yk′≤c′≤yk′+1;

步骤3核对是否k′=k,若满足，终止且设置c′=cl，k=L；否则，进入步骤4；

步骤4计算:

s=sign(k′-k)

且

c″(k′)=a′/b′

步骤5设置c′=c″(k),a=a′ 且b=b′并返回步骤2。

步骤1取k=[N/1.7](最接近N/1.7的整数)且计算:

c′=a/b

步骤2同(1)中的步骤2。

步骤3除了设置c′=cr,k=R，其它同(1)中的步骤3。

步骤4计算:

s=sign(k′-k)

且

c″(k′)=a′/b′

步骤5同(1)中的步骤5。

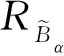
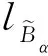
(23)

(24)

步骤1取c=a+(b-a)/2.4且计算：

c′=α/β

步骤2核对是否 |c′-c|<ε(ε为给定的边界误差),若满足，终止且设置c′=cl;否则，进入步骤3。

步骤3计算：

s=sign(c′-c),

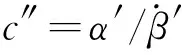
步骤4设置c=c′,c′=c″,α=α′,β=β′ 且返回步骤2。

步骤1取c=a+(b-a)/1.7且计算：

c′=α/β

步骤2核对是否 |c′-c|<ε(ε为给定的边界误差),若满足，终止且设置c′=cr;否则，进入步骤3；

步骤3计算：

s=sign(c′-c)

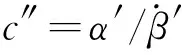
步骤4同(3)的步骤4。

(25)

最终的解模糊化输出可由端点平均解模糊化方法计算，如式(26)所示：

(26)

观察(1)～(4)，可总结出离散EKM算法和连续EKM算法的内在联系为：

(1) 离散EKM算法是基于离散点的求和运算计算完成广义二型模糊逻辑系统质心降型。当迭代终止时，取得的优化转折点可近似估计质心。连续EKM算法采用积分运算完成广义二型模糊逻辑系统质心降型。从理论上说，当主变量离散，采样点的个数趋于无穷时，离散EKM算法解就趋于连续EKM算法。

(2) 对于离散EKM算法，增加主变量采样个数可能会取得更准确的计算结果。对于连续EKM算法，控制相邻2次迭代的边界误差可提高算法的计算精度。

(3) 离散EKM算法用求和运算法完成数值计算。连续EKM算法用求积分运算完成象征性的计算。总结起来，离散EKM算法可看成在数值积分方法下CEKM算法的数值实现。

4 仿真实验

本节给出2个仿真例子。在例1中，输出广义二型模糊集的FOU为分段线性函数，相关次隶属函数(或称垂直切片)为梯形函数。在例2中，输出广义二型模糊集的FOU是由高斯型函数和分段线性函数组成，相关次隶属函数为三角形函数。这里假设广义二型模糊逻辑系统的质心输出广义二型模糊集已通过加权或聚合所有的激发模糊规则得出。此外，主变量用字母x表示。表1和图1给出了所定义的FOU，而表2和图2又给出了所定义的相关次隶属函数。

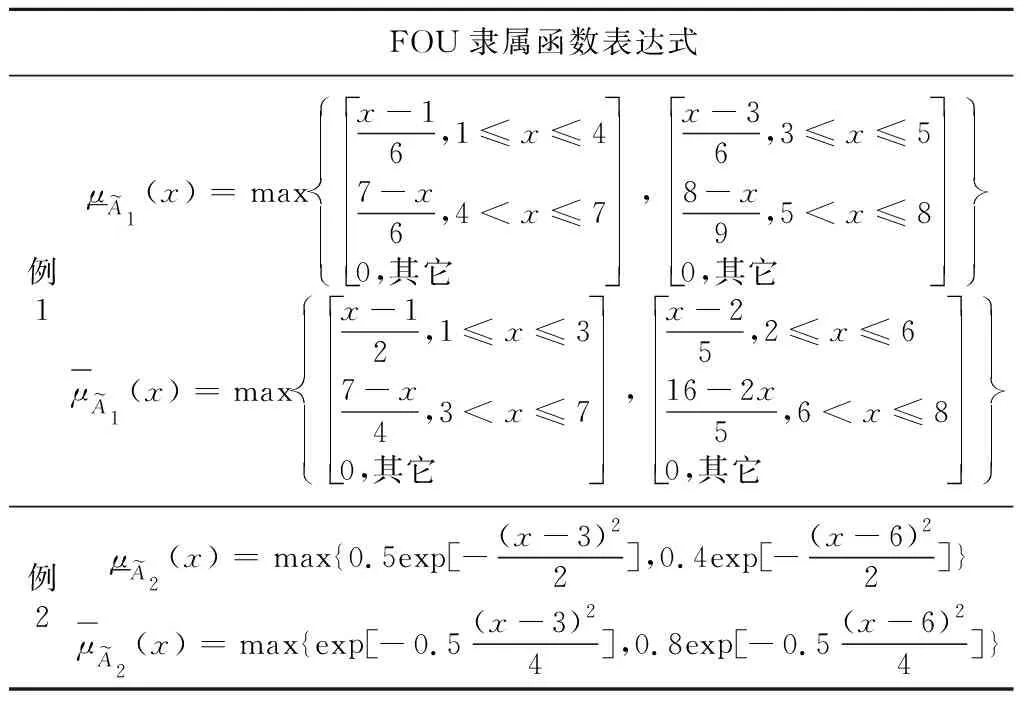
Table 1 Membership function expressions for FOU of example 1 and example 2表1 例1和例2的FOU隶属函数表达式

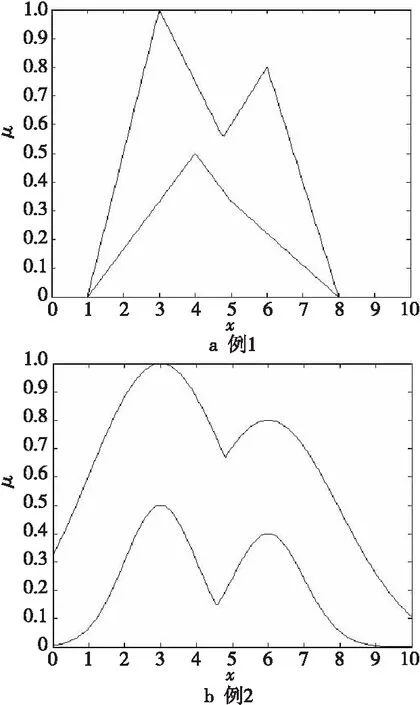
Figure 1 Graphs of FOU图1 FOU图

Table 2 Secondary membership function expressions of example 1 and example 2

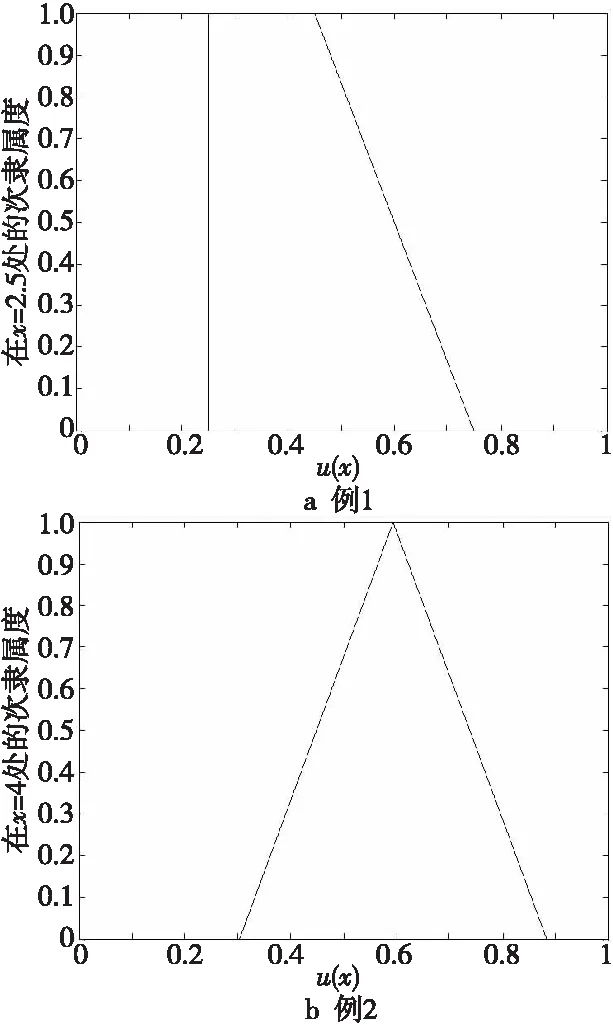
Figure 2 Shape graphs of secondary membership functions图2 次隶属函数形状图

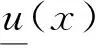
当Δ取最大值100时，由基准的CEKM算法计算出的质心降型集如图3所示。当Δ以1为步长从1到100变化时，基准的CEKM算法计算出的质心解模糊化值如图4所示。

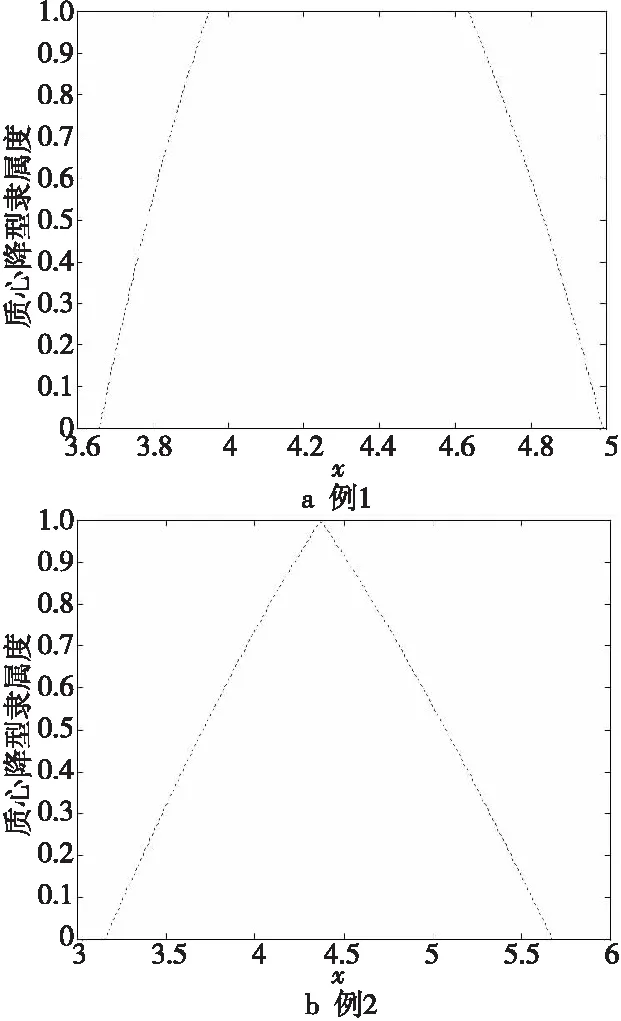
Figure 3 Centroid type-reduced sets computed by the CEKM algorithm图3 CEKM算法计算出的质心降型集

为了研究算法的计算精度，这里定义离散EKM算法和连续EKM算法在计算质心降型集和质心解模糊化值时的绝对误差。当取输出广义二型模糊集主变量采样点个数分别为20,50,100,200,3 000 和17 000时，2个算法计算的质心降型集左侧隶属函数和质心解模糊化值绝对误差分别如图5和图6所示。

为了进一步定量研究误差指标，表3和表4又分别给出了在上述采样点个数下离散EKM算法和连续EKM算法在计算质心降型集左侧隶属函数和质心解模糊化值时的绝对误差的平均值。

观察图5、图6、表3和表4，可以得出如下结论：

(1) 随着主变量采样个数的增加，无论是计算广义二型模糊逻辑系统的质心降型集还是质心解模糊化值，离散EKM算法的计算结果都会越来越接近连续EKM算法，如图5和图6所示。

Figure 4 Centroid defuzzified values computed by the CEKM algorithm图4 CEKM算法计算出的质心解模糊化值

(2) 在例1中，当取主变量采样个数为200时，离散EKM算法计算质心降型集的结果就与连续EKM算法的相同了；但在例2中(主隶属函数是非线性函数)，需要取采样个数为17 000才能使离散EKM算法计算质心降型集的结果与连续EKM算法的相同，如表3所示。

(3) 在计算质心解模糊化值时，当取主变量采样个数为17 000时，例2中离散EKM算法的计算结果就与连续EKM算法的相同了，而例1中离散EKM算法的计算结果仍然不能完全与连续EKM算法的相同，但误差(0.002 6)已经很小了(如表4所示)，可适当再增加采样个数使离散EKM计算结果与连续EKM算法的相同。

Table 3 Mean absolute errors of left membership functions on centroid type-reduced set表3 质心降型集左侧隶属函数的平均绝对误差

Table 4 Average mean absolute errors of centroid defuzzified values表4 质心解模糊化值平均值

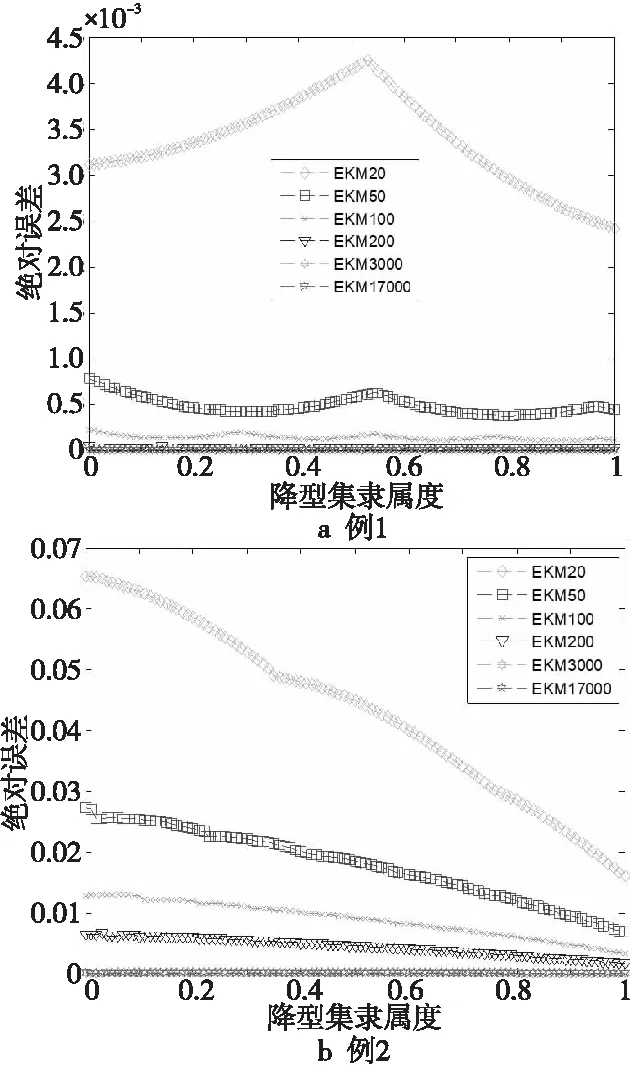
Figure 5 Absolute errors of left centroid membership functions computed by two algorithms图5 2个算法计算的质心降型集左侧隶属函数绝对误差值

Figure 6 Absolute errors of centroid defuzzified values computed by two algorithms图6 2个算法计算的质心解模糊化值绝对误差值

5 结束语

本文比较并给出了离散EKM算法和连续EKM算法之间的内在联系。基于α-平面表达理论，对于推理输出具有不同足迹不确定性和次隶属函数的广义二型模糊集，2个仿真实验表明了当适当增加主变量采样个数时，离散EKM算法在计算质心降型集和质心解模糊化值时可以较好地逼近连续EKM算法。

在以后的工作中，作者将基于各类迭代和非迭代降型算法[25,26]研究二型模糊逻辑系统的中心集降型[27]，以及基于智能优化算法的二型模糊逻辑系统在预测、模糊控制[28,29]和模糊系统辨识中的应用等。